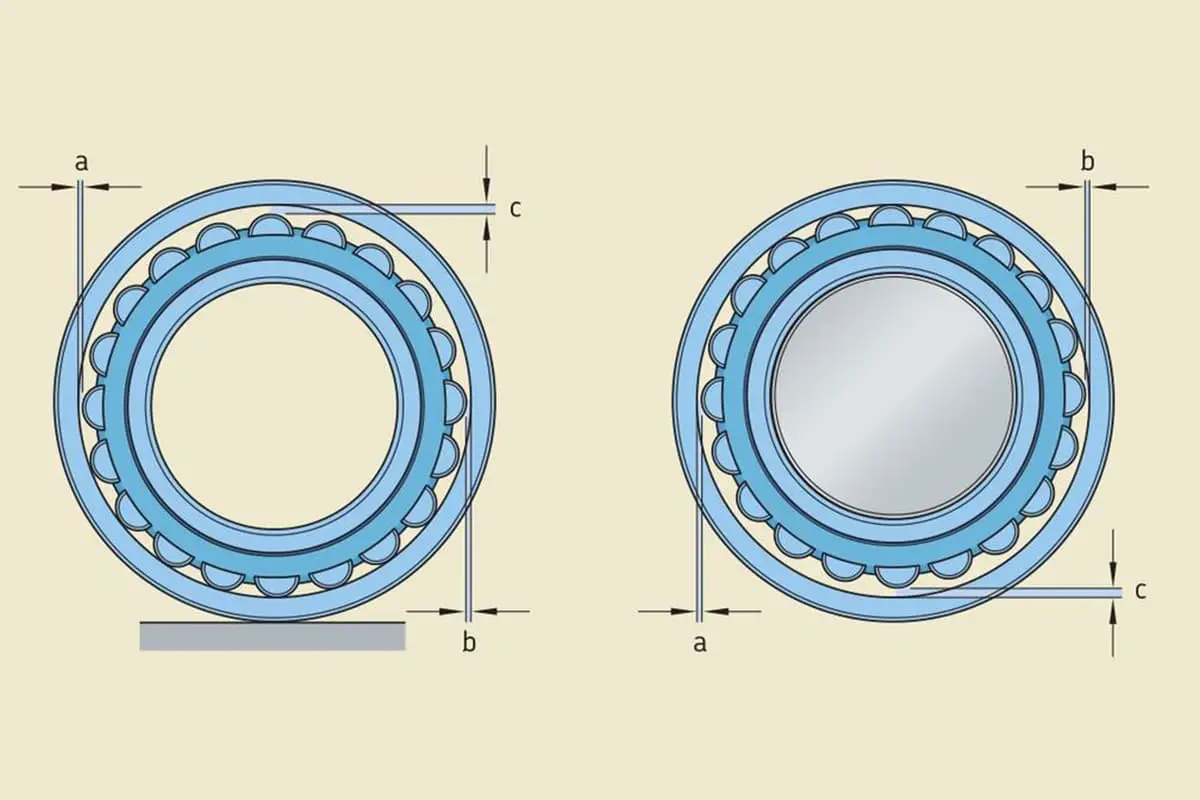
Vous êtes-vous déjà demandé quelle était la durée de vie d'un roulement ? Dans cet article de blog, nous allons explorer le concept de durée de vie des roulements et les facteurs qui l'influencent. Notre ingénieur mécanicien expérimenté décomposera les complexités et fournira des indications pour maximiser la longévité des roulements. Découvrez des conseils pratiques et des stratégies pour assurer le bon fonctionnement de vos roulements.
Nous avons déjà abordé la question du calcul de la durée de vie d'un roulement. Dans ces articles, nous avons principalement présenté les aspects théoriques de la durée de vie des roulements et la formule de calcul.
Aujourd'hui, nous visons à appliquer cette théorie à des scénarios pratiques. Après tout, le but ultime de l'acquisition de connaissances théoriques est de répondre aux besoins pratiques de l'ingénierie. Certains ingénieurs ont demandé des exemples de calculs concrets. Nous allons donc approfondir l'exemple de notre article précédent.
Reprenons l'exemple du moteur vertical. Voici les détails des roulements concernés :
Fournissons également quelques paramètres supplémentaires pour ce palier :
Vitesse de rotation : n=1500rpm
En utilisant la formule de durée de vie des roulements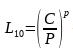
on obtient la durée de vie du roulement :
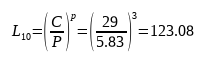
Ici, p est le coefficient de calcul du roulement. Lorsque l'élément roulant du roulement est une bille, p est égal à 3, et lorsque l'élément roulant est un rouleau, p est égal à 10/3. La durée de vie du roulement qui en résulte est de 123,08, en millions de tours. Convertie en une unité de temps plus courante, on obtient :
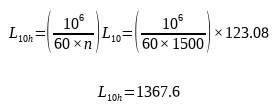
La durée de vie calculée des roulements est d'environ 1368 heures.
Dans cet exemple, nous avons utilisé un scénario dans lequel le roulement est soumis à une charge élevée. Le résultat du calcul suggère que le roulement n'est pas adapté à cette application en raison de sa courte durée de vie. Si le moteur fonctionne en continu, la durée de vie nominale de base ne peut assurer que moins de deux mois de fonctionnement du roulement.
En d'autres termes, si nous choisissons ce roulement, nous ne pouvons garantir que 90% des roulements peuvent fonctionner en continu pendant deux mois dans ces conditions.
Ce qui précède est la valeur de la durée de vie des roulements obtenue en utilisant la théorie de base de la durée de vie des roulements.
Cependant, comme vous l'avez peut-être remarqué, tout comme dans nos articles précédents, l'ensemble du processus de calcul ne prend en compte que la charge sur le roulement. En d'autres termes, cette durée de vie nominale des roulements ne tient compte que de l'impact de la charge. Comme nous l'avons expliqué dans nos articles précédents, après de nombreuses années de développement de la théorie moderne de la durée de vie des roulements, ce calcul ne répond plus à nos besoins. C'est pourquoi il est nécessaire d'ajuster cette valeur.
En d'autres termes, nous devons calculer la valeur de la durée de vie modifiée du roulement. La plupart des calculs ultérieurs n'utilisent pas de formules car ces calculs peuvent être complexes, de nombreux processus ou théories de référence proviennent d'expériences et, troisièmement, divers fournisseurs de roulements et normes internationales de roulements nous ont fourni un meilleur outil de référence : les diagrammes. Alors, comment utiliser ces tableaux ? Explorons-le à l'aide de notre exemple.
Comme indiqué dans nos articles précédents, la formule de calcul de la durée de vie ajustée est la suivante :
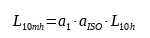
Pour déterminer la valeur finale de L10mh nous devons définir a1 et aiso.
01 Tout d'abord, nous définissons a1.
Comme nous l'avons vu précédemment, a1 est le coefficient de fiabilité de la durée de vie ajustée. Lorsque la fiabilité est de 90%, la valeur de a1 est de 1. Pour les machines d'usage général utilisées dans l'industrie, sauf exigence spécifique, la durée de vie du roulement est toujours basée sur une fiabilité de 90%. Par conséquent, dans cet exemple, nous pouvons directement prendre a1.
02 Deuxièmement, nous trouvons uniso.
La méthode standard de calcul du coefficient de durée de vie ajustée aiso d'un roulement prend en compte les facteurs suivants :
En résumé, uniso est fonction des paramètres suivants :
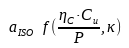
Où ?
Tout d'abord, nous sélectionnons le facteur de contamination ηc du roulement. Dans la norme ISO281 et toutes les normes fabricant de roulements il existe une table de référence pour les critères de sélection comme suit :
| Pollution | Coefficient ec | |
| dm<100mm1) | dm≥100mm1) | |
| Extrêmement propre -Taille des particules inférieure à l'épaisseur du film d'huile -Conditions de laboratoire | 1 | 1 |
| Très propre -Huile filtrée par des filtres ultrafins -Roulements lubrifiés avec de la graisse scellée | 0.8-0.6 | 0.9-0.8 |
| Propreté standard -Huile filtrée par des filtres à maille fine | 0.6-0.5 | 0.8-0.6 |
| Pollution lumineuse -Légère contamination de l'huile de lubrification | 0.5-0.3 | 0.6-0.4 |
| Pollution générale -contamination des roulements par des particules abrasives sur d'autres pièces mécaniques | 0.3-0.1 | 0.4-0.2 |
| Pollution grave -L'environnement dans lequel le roulement est utilisé est gravement pollué. -Mauvaise étanchéité du palier | 0.1-0 | 0.1-0 |
| Pollution extrême | 0 | 0 |
Dans l'application des moteurs verticaux, sur la base de notre expérience antérieure, le facteur de contamination des roulements doit être choisi entre la pollution lumineuse et la propreté générale. Dans le cas présent, nous choisissons un facteur de contamination de 0,6, ce qui est légèrement supérieur à la propreté générale.
Permettez-moi d'ajouter,
La sélection du facteur de contamination ne fait pas l'objet d'une formule mathématique spécifique. Elle s'appuie généralement sur des années de application des roulements l'expérience. Plus nous rencontrons d'applications, plus nous obtenons d'informations sur cette sélection.
Le roulement choisi étant le 6208, la limite de charge de fatigue Cu de ce roulement est indiqué dans le catalogue des roulements : 1.05kN
La valeur de la charge dynamique équivalente du palier a été calculée dans le chapitre précédent et s'élève à P=5,83kN.
Nous pouvons donc obtenir une valeur approximative :
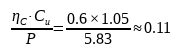
Ensuite, nous devons faire un choix un peu plus complexe du rapport de viscosité k. En raison de l'espace limité de ce chapitre, nous ne nous étendrons pas sur la signification spécifique de k et sur la manière de choisir cette valeur. Nous écrirons un autre article pour le détailler plus tard. Pour l'instant, nous voulons seulement souligner que pour les roulements, le choix de la bonne lubrification est très important. Cela ne concerne pas seulement la qualité de la graisse elle-même, mais aussi l'impact de la lubrification sur les roulements.
En ce qui concerne le rapport de viscosité,
D'une manière générale, nous espérons que la valeur de lubrification finale de k pourra être choisie entre 1 et 4, en tenant compte de plusieurs considérations.
Si la valeur k calculée de la valeur de lubrification sélectionnée est :
Nous avons donc choisi une valeur de lubrification appropriée, et la valeur finale de k est de 1,5.
Avec ces deux paramètres, on peut trouver le tableau suivant dans la norme ISO281 ou dans le catalogue du fabricant de roulements.
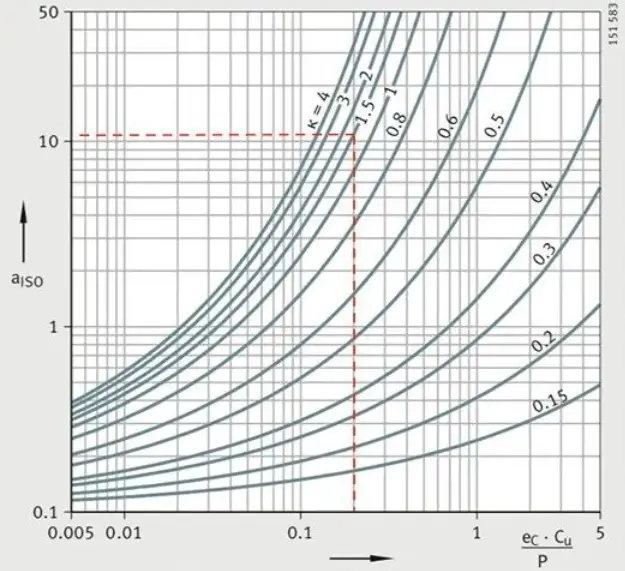
Attention !
Il existe plusieurs diagrammes similaires, chacun pour différents types de roulements. Nous avons choisi le roulement à billes à gorge profonde, qui est un type de roulement radial à billes. Il convient donc de sélectionner le diagramme approprié en fonction du type de roulement.
Le diagramme choisi nous permet de déterminer que, dans cette application, aiso=12.
Dans cet exemple, la durée de vie nominale corrigée finale du roulement 6208 est la suivante :
L10mh = a1×aiso×L10h = 1×12×1367.6 = 16411.2
Dans ce moteur vertical, dans des conditions de lubrification appropriées, le roulement peut fonctionner pendant 16 410 heures.
Étant donné que le résultat du calcul de la durée de vie des roulements ne peut pas refléter exactement la durée de vie réelle des roulements, quel est l'objectif de ce calcul ?
En fait, de nombreux ingénieurs confondent le calcul de la durée de vie avec la "cartomancie", probablement en raison de son nom. À l'origine, l'étude de la durée de vie en fatigue des roulements avait pour but d'établir une valeur de référence, une référence de durée de vie. Au fil du temps, cette valeur de référence est devenue un paramètre permettant de comparer et de vérifier le bien-fondé de la sélection des roulements.
En fait, le calcul de la durée de vie des roulements est une vérification de la capacité de charge du roulement choisi. En d'autres termes, il s'agit de choisir le plus petit roulement qui puisse répondre à l'exigence de durée de vie. En ce sens, le calcul de la durée de vie des roulements est une exigence pour la limite inférieure de la capacité de charge des roulements.
Comment comprendre cela ? Commençons par le processus de vérification de la vie :
Lorsque les ingénieurs vérifient la durée de vie des roulements, les manuels de conception mécanique et les matériaux d'équipement fournissent toujours des valeurs minimales pour les exigences de durée de vie. Voici un exemple :
| Conditions de fonctionnement : | Types de machines | Durée de vie requise du palier (temps, h) |
| Fonctionnement à court terme ou intermittent | Appareils ménagers et outils électriques, machines agricoles, treuils. | 4000~8000 |
| Utilisation peu fréquente mais fonctionnement fiable requis | Climatiseurs domestiques, machines de construction, convoyeurs à bande, ascenseurs. | 8000~12000 |
| Fonctionnement non continu mais prolongé | Cols de rouleaux de laminoirs, petits moteurs électriques, grues. | 8000~12 000 |
| Moteurs électriques généraux, dispositifs généraux à engrenages. | 12 000~20 000 | |
| Machines-outils, cribles vibrants, concasseurs. | 20000~30 000 | |
| Compresseurs, pompes, dispositifs à engrenages cruciaux. | 40000~60 000 | |
| Fonctionnement constant pendant plus de 8 heures par jour ou fonctionnement continu à long terme | Escaliers mécaniques. | 12 000~20 000 |
| Séparateurs centrifuges, équipements de climatisation, ventilateurs, machines à travailler le bois, essieux de véhicules ferroviaires. | 20000~30 000 | |
| Grands moteurs électriques, treuils de mine, moteurs électriques principaux pour véhicules ferroviaires, essieux de locomotives. | 40000~60 000 | |
| Machines à papier. | 100000~200000 | |
| Fonctionnement ininterrompu et sans faille pendant 24 heures | Équipement d'approvisionnement en eau, équipement de centrale électrique, équipement de drainage minier. | 100000~200000 |
Certes, certains fabricants d'équipements imposent des exigences différentes en matière de durée de vie. Souvent, ces valeurs de durée de vie sont respectées par les roulements dans les conceptions traditionnelles.
Ainsi, lors de la conception de nouveaux équipements et de la vérification de la durée de vie des roulements, l'approche suivante peut être utilisée :
Un choix trop petit ou trop grand doit se situer dans une fourchette raisonnable, et l'égalité absolue ne doit pas être recherchée. Par conséquent, lorsque l'on observe la "durée de vie requise", on s'aperçoit que cette valeur est une fourchette et non une valeur absolue.
Par conséquent, le calcul implicite de la durée de vie d'un roulement implique de vérifier la capacité de charge du roulement dans des conditions de durée de vie raisonnables. En d'autres termes, il faut choisir un roulement de taille raisonnable dans des conditions de travail données.
Dans la vie réelle, de nombreuses "erreurs de manipulation" se produisent en raison d'une mauvaise compréhension des concepts susmentionnés :
(1) La durée de vie calculée d'un roulement doit correspondre à la période de garantie de l'équipement.
Cette pratique confond la vérification de la charge du roulement avec la durée de vie de l'équipement. En effet, la vérification de la durée de vie d'un roulement n'est pas équivalente à une "voyance", comme nous l'avons expliqué dans l'article précédent.
Les conditions réelles des roulements sont variées et les ingénieurs ne peuvent pas calculer chaque machine individuellement. Il s'agit là d'un malentendu de la part des fabricants d'équipements concernant le "calcul de la durée de vie des roulements".
Le concept de période de garantie place toute la responsabilité sur le fabricant de l'équipement, un concept de "garantie" qui est beaucoup plus large que le concept couvert par le "calcul de la durée de vie des roulements", ce qui rend une telle application directe inappropriée.
Bien entendu, certains ingénieurs, sous la pression du client, sont contraints de respecter une durée de vie de "20 ans". Dans ce cas, les roulements choisis sont souvent surdimensionnés, ce qui se traduit non seulement par une inefficacité économique, mais aussi par une méconnaissance du fait que des calculs de durée de vie plus importants ou plus longs ne sont pas toujours préférables pour les roulements.
(2) Plus la durée de vie calculée d'un roulement est longue, mieux il se porte.
En fait, cela induit également en erreur lors de la sélection des roulements. Comme je l'ai mentionné précédemment, le calcul de la durée de vie des roulements est une vérification de la capacité de charge minimale des roulements dans des conditions de travail.
D'autre part, il doit également y avoir une limite à la capacité de charge maximale des roulements, qui est la limite supérieure de la capacité de charge des roulements dans les conditions de travail. Si le résultat du calcul dépasse cette valeur, des problèmes surviendront avec le roulement.
C'est ce que nous appelons souvent la "charge minimale du roulement". Si le roulement choisi est trop grand et que la durée de vie calculée du roulement dans des conditions de travail est longue, ce qui signifie que la capacité de charge du roulement est très élevée, il se peut que la charge minimale du roulement ne soit pas respectée.
Si la charge supportée par le roulement est inférieure à la charge minimale requise, des problèmes tels que le glissement des éléments roulants peuvent survenir à l'intérieur du roulement, le rendant plus susceptible de griller.
En effet, la compréhension du concept de durée de vie des roulements peut conduire à de nombreuses optimisations dans la conception. Il s'agit notamment de
Évaluer s'il est possible de réduire la taille du roulement tout en respectant les exigences de durée de vie ;
Tenir un registre de la durée de vie de nombreux roulements et envisager une réduction supplémentaire de la taille s'il reste une durée de vie résiduelle.
En résumé, dans la pratique de l'ingénierie, le calcul de la durée de vie d'un roulement est utilisé pour vérifier la capacité de charge du roulement, et non pour la maximiser. En outre, cette durée calculée ne reflète pas la "véritable" durée de vie du roulement.
Une compréhension précise des concepts de durée de vie des roulements permet de sélectionner correctement les dimensions des roulements.
Malheureusement, dans le cadre de notre travail, nous devons parfois nous plier aux exigences de nos clients, même si nous pensons que leurs demandes sont techniquement déraisonnables. N'hésitez donc pas à partager cet article avec eux.
Il s'agit peut-être de l'article le plus difficile à comprendre du site jusqu'à présent, en particulier pour les ingénieurs électriciens. Si vous avez des questions, n'hésitez pas à laisser un commentaire pour en discuter.
En tant que fondateur de MachineMFG, j'ai consacré plus d'une décennie de ma carrière à l'industrie métallurgique. Ma vaste expérience m'a permis de devenir un expert dans les domaines de la fabrication de tôles, de l'usinage, de l'ingénierie mécanique et des machines-outils pour les métaux. Je suis constamment en train de réfléchir, de lire et d'écrire sur ces sujets, m'efforçant constamment de rester à la pointe de mon domaine. Laissez mes connaissances et mon expertise être un atout pour votre entreprise.
FR 
EN 
AR 
DE 
ES 
IT 
NL 
PT 
RU