Vous êtes-vous déjà demandé comment calculer avec précision la surépaisseur de pliage pour vos projets de fabrication métallique ? Dans cet article de blog, nous allons explorer le monde fascinant des formules et des calculs de la surépaisseur de pliage. En tant qu'ingénieur mécanique expérimenté, je vous guiderai à travers les concepts clés et vous donnerai des conseils pratiques pour vous aider à maîtriser cet aspect crucial de la conception de tôles. Préparez-vous à plonger et à percer les secrets de la création de pliages précis et efficaces dans vos projets !
La surépaisseur de pliage est un concept essentiel dans le domaine de la fabrication de tôles, en particulier lors des opérations de pliage. Il s'agit de la longueur supplémentaire de matériau nécessaire pour accueillir le pliage de la tôle. Il est essentiel de comprendre et de calculer avec précision la surépaisseur de pliage pour s'assurer que les dimensions finales de la pièce pliée sont conformes aux spécifications de la conception.
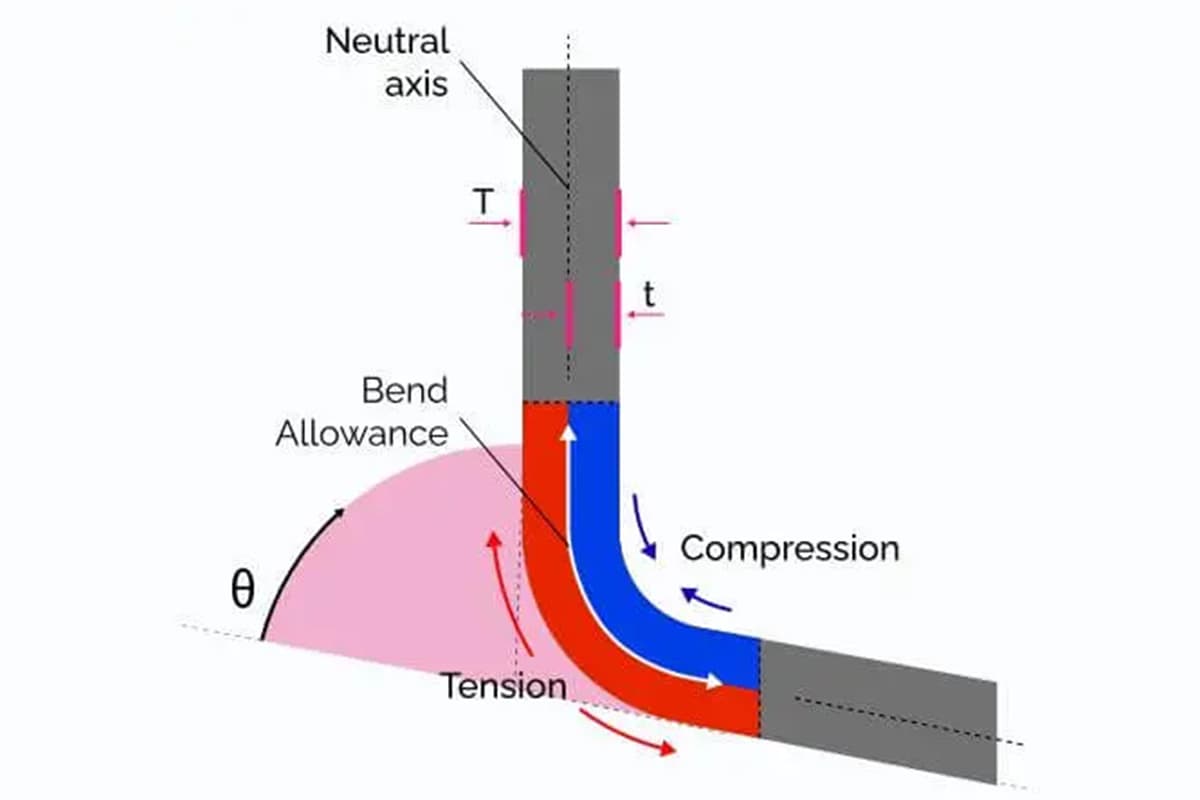
Le calcul précis de la surépaisseur de pliage est essentiel dans le processus de fabrication. Lorsqu'une tôle plate est pliée, le matériau situé à l'extérieur du pli s'étire, tandis que le matériau situé à l'intérieur se comprime. Si cette déformation n'est pas prise en compte, le produit final ne correspondra pas à la conception prévue, ce qui entraînera des imprécisions et des défaillances potentielles. La surépaisseur de pliage aide les fabricants à ajuster les dimensions du modèle plat, garantissant ainsi que la pièce pliée répond à des exigences précises.
Plusieurs paramètres critiques influencent le calcul de la tolérance de pliage :
Le concept de indemnité de pliage est la suivante : lorsqu'une feuille de métal est pliée, elle a trois dimensions - deux dimensions extérieures (L1 et L2) et une dimension d'épaisseur (T).
Il est important de noter que la somme de L1 et L2 est supérieure à la longueur dépliée (L), et que la différence entre les deux est connue sous le nom de marge de flexion (K).
Par conséquent, la longueur dépliée d'un coude peut être calculée comme L = L1 + L2 - K.
Lecture connexe :
Comment la formule de indemnité de pliage créé ? Et comment calculer indemnité de pliage?
La surépaisseur de pliage dépend du rayon intérieur formé. L'ouverture de la matrice en V inférieur détermine le rayon intérieur (R.I.) d'une pièce formée. Le rayon intérieur pour l'acier doux est de 5/32 x l'ouverture inférieure de la matrice en V (W) lorsque le rayon du poinçon est inférieur à 5/32 x W.
Si I.R.< Epaisseur du matériau (t)
Si I.R.> 2 x épaisseur du matériau (t)
Où A= (180 - Angle inclus dans le pli)
Si le rayon intérieur est égal à t ou 2t, ou compris entre t et 2t, la surépaisseur de pliage est calculée en interpolant les valeurs de surépaisseur de pliage des deux formules mentionnées ci-dessus.
En outre, pour calculer cette indemnité de flexion, vous pouvez également utiliser la formule suivante :
Cette formule prend en compte les différentes géométries et propriétés des pièces à former.
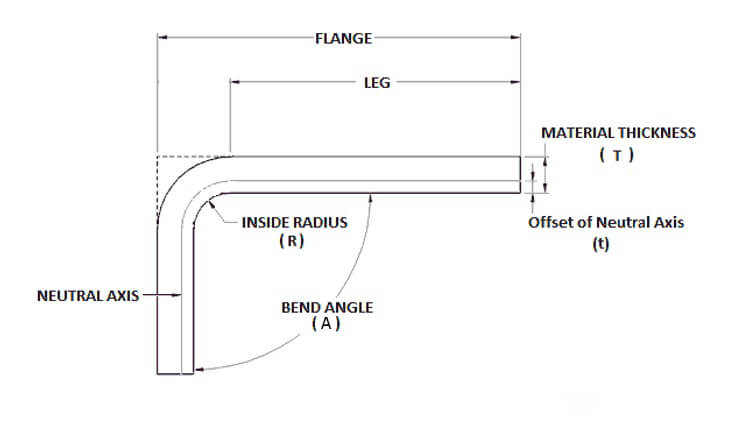
L'épaisseur du matériau (T), l'angle de flexion (A), l'épaisseur intérieure (A) et l'angle de flexion (B) sont des facteurs déterminants. rayon de courbure (R), et le facteur K du matériau à plier sont les facteurs les plus critiques dans ce calcul.
Comme le montre la formule ci-dessus, le calcul de la marge de flexion est un processus simple.
Vous pouvez déterminer la marge de flexion en remplaçant les valeurs susmentionnées dans la formule.
Lorsque l'angle de flexion est de 90°, la formule de la marge de flexion peut être simplifiée comme suit :
Note : Le facteur K pour la plupart des matériaux et épaisseurs standard se situe généralement entre 0 et 0,5.
Vous pouvez calculer avec précision la valeur du facteur K en procédant comme suit Calculateur du facteur K:
La formule de la surépaisseur de pliage (BA) est essentielle pour calculer la longueur de matériau nécessaire à la formation d'un pli. Cette formule générale est largement applicable à différents matériaux et méthodes de pliage :
Où ?
Le facteur K est crucial car il indique la position de l'axe neutre, qui ne change pas de longueur pendant le pliage. Le facteur K se situe généralement entre 0,3 et 0,5 et varie en fonction du type de matériau, de l'épaisseur, du rayon et de la méthode de pliage.
Les différents matériaux ont des propriétés uniques qui nécessitent des ajustements dans les calculs de la tolérance de pliage. Ces ajustements garantissent la précision, en particulier pour les coudes à 90° :
Pour les matériaux plus tendres comme le laiton ou le cuivre, la marge de pliage est calculée comme suit :
BA = (0,55 × T) + (1,57 × R
Cet ajustement tient compte de la ductilité du matériau et de sa moindre résistance à la déformation.
Pour le cuivre ou le laiton semi-dur, l'acier doux et l'aluminium, la tolérance de pliage est de :
BA = (0,64 x T) + (1,57 × R)
Ces matériaux ont une dureté modérée et nécessitent une surépaisseur légèrement supérieure à celle des matériaux plus tendres.
Pour les matériaux plus durs tels que le bronze, le cuivre dur, l'acier laminé à froid et l'acier à ressort, la formule est la suivante :
BA = (0,71 x T) + (1,57 × R)
Ces matériaux sont plus résistants à la flexion, ce qui nécessite une allocation plus élevée.
Pour déterminer la longueur totale à plat de la pièce de tôle, la surépaisseur de pliage est ajoutée aux longueurs des parties plates :
Longueur plate = Longueur de la jambe 1 + BA + Longueur de la jambe 2
Cette approche garantit que les dimensions finales de la pièce sont exactes après le pliage.
Considérons un pli à 90° dans une feuille d'aluminium d'une épaisseur de 2 mm et d'un rayon de courbure intérieur de 5 mm. En utilisant la formule spécifique au matériau pour le cuivre semi-dur, le laiton, l'acier doux et l'aluminium :
BA = (0,64 × 2) + (1,57 × 5)
BA = 1,28 + 7,85=9,13
Si la pièce comporte deux sections plates de 50 mm chacune, la longueur totale de la section plate est la suivante :
Longueur du plat = 50 + 9,13 + 50 = 109,13 mm
En plus de la marge de pliage, la déduction de pliage (BD) et le retrait extérieur (OSSB) sont importants pour obtenir des mesures précises :
Déduction pour courbure (DC) = OSSB - BA
Où ?
Ces formulations et considérations sont essentielles pour calculer avec précision les surépaisseurs de pliage et garantir que les pièces de tôle sont fabriquées avec les dimensions et l'ajustement corrects.
La surépaisseur de pliage est un facteur essentiel dans le processus de pliage des tôles, en particulier pour les matériaux tels que l'aluminium. Elle tient compte de l'étirement du matériau qui se produit pendant le pliage, ce qui garantit la précision des dimensions finales. Nous examinerons ici la formule spécifique utilisée pour les tôles d'aluminium et son application.
La surépaisseur de pliage d'une plaque d'aluminium peut être calculée à l'aide de la formule suivante :
𝐿=𝐿1+𝐿2-1.6𝑇
Où ?
La valeur de 1,6𝑇 est dérivée de manière empirique, ce qui signifie qu'elle a été établie à partir d'expériences pratiques et de l'expérience de la production. Ce facteur tient compte du comportement du matériau pendant la flexion, ce qui garantit la précision des dimensions finales.
Il est essentiel de noter que cette formule est spécifiquement applicable sous certaines conditions :
Pour déterminer la taille de la plaque d'aluminium, procédez comme suit :
Ce calcul vous donnera la longueur du modèle plat nécessaire avant le pliage, ce qui garantit que la pièce pliée finale a les bonnes dimensions.
Le calculateur de surépaisseur de pliage ci-dessous simplifie le processus de calcul de la surépaisseur de pliage, qui est essentiel pour une fabrication précise de la tôle. La surépaisseur de pliage est la longueur de l'axe neutre entre les lignes de pliage, ce qui permet de déterminer la taille correcte de l'ébauche pour une pièce pliée.
L'angle de pliage, noté θ, est un paramètre crucial dans la formule de la surépaisseur de pliage. Il représente l'angle de pliage de la tôle. L'angle de pliage est généralement mesuré en degrés, mais peut être converti en radians à l'aide de la formule :
Le rayon intérieur, représenté par r, est le rayon de la courbe intérieure du pli. Ce rayon influence directement la quantité d'étirement et de compression qui se produit à l'intérieur du matériau pendant le pliage. Un rayon intérieur plus petit entraîne une déformation plus importante, qui doit être prise en compte dans le calcul de la tolérance au pliage.
L'épaisseur du matériau, désignée par T, est l'épaisseur de la tôle à plier. Les matériaux plus épais subissent des étirements et des compressions plus prononcés, ce qui affecte la tolérance de pliage globale. Une mesure précise de l'épaisseur du matériau est essentielle pour un calcul précis de la surépaisseur de pliage.
Le facteur K est une valeur sans dimension qui représente la position de l'axe neutre par rapport à l'épaisseur du matériau. L'axe neutre est la ligne théorique à l'intérieur du matériau dont la longueur reste inchangée pendant la flexion. Le facteur K varie en fonction des propriétés du matériau et des méthodes de pliage, et se situe généralement entre 0,3 et 0,5 pour la plupart des matériaux. La formule pour la position de l'axe neutre est la suivante
Position de l'axe neutre = K × T
L'axe neutre est la ligne imaginaire à l'intérieur du matériau dont la longueur reste inchangée pendant le pliage. Il est essentiel de comprendre sa position pour calculer la surépaisseur de pliage correcte.
La surépaisseur de pliage, représentée par BA, est la longueur de l'axe neutre nécessaire pour former un pli. Elle est calculée à l'aide de la formule suivante
Cette formule utilise l'angle de courbure, le rayon intérieur, l'épaisseur du matériau et le facteur K pour garantir des calculs précis de la marge de courbure.
Le tableau des tolérances de pliage est une ressource essentielle pour les professionnels travaillant dans la fabrication de tôles. Il fournit une liste complète des paramètres clés tels que l'épaisseur du matériau, le rayon de courbure, l'angle de courbure, la surépaisseur de courbure et les valeurs de déduction de courbure pour les matériaux courants. Ces informations sont essentielles pour calculer avec précision la longueur de développement d'une pièce de tôle après pliage.
Pour en savoir plus :
| TV | Angle | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Taille la plus courte |
| V4 | 90 | 0.9 | 1.4 | 2.8 | ||||||||||
| V4 | 120 | 0.7 | ||||||||||||
| V4 | 150 | 0.2 | ||||||||||||
| V6 | 90 | 1.5 | 1.7 | 2.15 | 4.5 | |||||||||
| V6 | 120 | 0.7 | 0.86 | 1 | ||||||||||
| V6 | 150 | 0.2 | 0.3 | 0.4 | ||||||||||
| V7 | 90 | 1.6 | 1.8 | 2.1 | 2.4 | 5 | ||||||||
| V7 | 120 | 0.8 | 0.9 | 1 | ||||||||||
| V7 | 150 | 0.3 | 0.3 | 0.3 | ||||||||||
| V8 | 90 | 1.6 | 1.9 | 2.2 | 2.5 | 5.5 | ||||||||
| V8 | 30 | 0.3 | 0.34 | 0.4 | 0.5 | |||||||||
| V8 | 45 | 0.6 | 0.7 | 0.8 | 1 | |||||||||
| V8 | 60 | 1 | 1.1 | 1.3 | 1.5 | |||||||||
| V8 | 120 | 0.8 | 0.9 | 1.1 | 1.3 | |||||||||
| V8 | 150 | 0.3 | 0.3 | 0.2 | 0.5 | |||||||||
| V10 | 90 | 2.7 | 3.2 | 7 | ||||||||||
| V10 | 120 | 1.3 | 1.6 | |||||||||||
| V10 | 150 | 0.5 | 0.5 | |||||||||||
| V12 | 90 | 2.8 | 3.65 | 4.5 | 8.5 | |||||||||
| V12 | 30 | 0.5 | 0.6 | 0.7 | ||||||||||
| V12 | 45 | 1 | 1.3 | 1.5 | ||||||||||
| V12 | 60 | 1.7 | 2 | 2.4 | ||||||||||
| V12 | 120 | 1.4 | 1.7 | 2 | ||||||||||
| V12 | 150 | 0.5 | 0.6 | 0.7 | ||||||||||
| V14 | 90 | 4.3 | 10 | |||||||||||
| V14 | 120 | 2.1 | ||||||||||||
| V14 | 150 | 0.7 | ||||||||||||
| V16 | 90 | 4.5 | 5 | 11 | ||||||||||
| V16 | 120 | 2.2 | ||||||||||||
| V16 | 150 | 0.8 | ||||||||||||
| V18 | 90 | 4.6 | 13 | |||||||||||
| V18 | 120 | 2.3 | ||||||||||||
| V18 | 150 | 0.8 | ||||||||||||
| V20 | 90 | 4.8 | 5.1 | 6.6 | 14 | |||||||||
| V20 | 120 | 2.3 | 3.3 | |||||||||||
| V20 | 150 | 0.8 | 1.1 | |||||||||||
| V25 | 90 | 5.7 | 6.4 | 7 | 17.5 | |||||||||
| V25 | 120 | 2.8 | 3.1 | 3.4 | ||||||||||
| V25 | 150 | 1 | 1 | 1.2 | ||||||||||
| V32 | 90 | 7.5 | 8.2 | 22 | ||||||||||
| V32 | 120 | 4 | ||||||||||||
| V32 | 150 | 1.4 | ||||||||||||
| V40 | 90 | 8.7 | 9.4 | 28 | ||||||||||
| V40 | 120 | 4.3 | 4.6 | |||||||||||
| V40 | 150 | 1.5 | 1.6 |
| TV | Angle | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Taille la plus courte |
| V4 | 1.4 | 2.8 | ||||||||||||
| V6 | 1.6 | 4.5 | ||||||||||||
| V7 | 1.6 | 1.8 | 5 | |||||||||||
| V8 | 1.8 | 2.4 | 3.1 | 5.5 | ||||||||||
| V10 | 2.4 | 3.2 | 7 | |||||||||||
| V12 | 2.4 | 3.2 | 8.5 | |||||||||||
| V14 | 3.2 | 10 | ||||||||||||
| V16 | 3.2 | 4 | 4.8 | 11 | ||||||||||
| V18 | 4.8 | 13 | ||||||||||||
| V20 | 4.8 | 14 | ||||||||||||
| V25 | 4.8 | 5.4 | 6 | 17.5 | ||||||||||
| V32 | 6.3 | 6.9 | 22 |
| Angle | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Taille la plus courte |
| 90 | 3.6 | 5.2 | 6.8 | 8.4 | 28 | ||||||||
| 120 | |||||||||||||
| 150 |
| MATÉRIAU | SPCC | SUS | Al （LY12） | SECC | ||||
|---|---|---|---|---|---|---|---|---|
| T | ΔT | ΔK | ΔT | ΔK | ΔT | ΔK | ΔT | ΔK |
| T=0.6 | 1.25 | 1.26 | ||||||
| T=0.8 | 0.18 | 1.42 | 0.15 | 1.45 | 0.09 | 1.51 | ||
| T=1.0 | 0.25 | 1.75 | 0.20 | 1.80 | 0.30 | 1.70 | 0.38 | 1.62 |
| T=1.2 | 0.45 | 1.95 | 0.25 | 2.15 | 0.50 | 1.90 | 0.43 | 1.97 |
| T=1.4 | 0.64 | 2.16 | ||||||
| T=1.5 | 0.64 | 2.36 | 0.50 | 2.50 | 0.70 | 2.30 | ||
| T=1.6 | 0.69 | 2.51 | ||||||
| T=1.8 | 0.65 | 3.00 | ||||||
| T=1.9 | 0.60 | 3.20 | ||||||
| T=2.0 | 0.65 | 3.35 | 0.50 | 3.50 | 0.97 | 3.03 | 0.81 | 3.19 |
| T=2.5 | 0.80 | 4.20 | 0.85 | 4.15 | 1.38 | 3.62 | ||
| T=3.0 | 1.00 | 5.00 | 5.20 | 1.40 | 4.60 | |||
| T=3.2 | 1.29 | 5.11 | ||||||
| T=4.0 | 1.20 | 6.80 | 1.00 | 7.00 | ||||
| T=5.0 | 2.20 | 7.80 | 2.20 | 7.80 | ||||
| T=6.0 | 2.20 | 9.80 | ||||||
Remarque :
Un tableau de surépaisseur de pliage bien tenu est un outil essentiel dans l'industrie de la fabrication de tôles. Il garantit la précision et l'efficacité du processus de pliage, ce qui permet d'obtenir des produits finis plus précis et de meilleure qualité. En comprenant et en utilisant les valeurs fournies dans le tableau, les ingénieurs et les fabricants peuvent obtenir des résultats optimaux dans leurs projets.
Dans la fabrication de tôles, la précision et l'exactitude sont essentielles pour créer des pièces de haute qualité. L'un des facteurs clés qui jouent un rôle important dans ce processus est le facteur K. Comprendre le facteur K et son application dans le calcul de la tolérance au pliage est essentiel pour que les fabricants produisent des pièces qui répondent à des spécifications exactes et fonctionnent de manière fiable dans diverses industries.
Le facteur K est une valeur sans dimension qui représente le rapport entre la distance de l'axe neutre et l'épaisseur du matériau. Il est essentiel pour calculer avec précision la surépaisseur de pliage, qui détermine la quantité de matériau nécessaire pour obtenir un pliage souhaité. L'axe neutre est une ligne imaginaire à l'intérieur du matériau dont la longueur ne change pas pendant le pliage. En comprenant le facteur K, les fabricants peuvent prédire comment le matériau se comportera lorsqu'il sera plié, ce qui garantit des processus de fabrication précis et efficaces.
Le facteur K est calculé à l'aide de la formule suivante :
Où ?
L'utilisation du facteur K dans la formule de surépaisseur de pliage permet de prévoir l'allongement et la compression du matériau pendant le pliage. La formule de la surépaisseur de pliage est la suivante :
Pour illustrer cela, prenons un exemple simple. Supposons une pièce de tôle d'une épaisseur (T) de 2 mm, pliée à un angle de 90 degrés (θ), avec un rayon intérieur (r) de 5 mm et un facteur K (K) de 0,4.
1. Convertir l'angle de courbure en radians :
2. Appliquer les valeurs à la formule de la marge de flexion :
Ce calcul montre qu'il faut environ 9,11 mm de matériau le long de l'axe neutre pour obtenir la courbure souhaitée, ce qui démontre l'importance d'un facteur K précis.
Le facteur K a un impact direct sur la précision des calculs de la surépaisseur de pliage. Un facteur K précis garantit que les dimensions finales de la pièce pliée correspondent aux spécifications de la conception, ce qui réduit le gaspillage de matériaux et la nécessité d'effectuer des retouches. Cette précision est vitale pour les industries où les dimensions exactes sont cruciales pour l'assemblage et la fonctionnalité des composants.
Les différents matériaux ont des propriétés mécaniques uniques, qui se traduisent par des valeurs variables du facteur K. Les matériaux plus tendres, comme l'aluminium, ont généralement un facteur K plus faible. Les matériaux plus souples comme l'aluminium ont généralement un facteur K plus faible, tandis que les matériaux plus durs comme l'acier inoxydable ont un facteur K plus élevé. La compréhension de ces variations permet aux fabricants de sélectionner les valeurs de facteur K appropriées pour les différents matériaux, ce qui garantit des calculs précis et des processus de fabrication efficaces.
Vous trouverez ci-dessous les réponses à certaines questions fréquemment posées :
La formule de surépaisseur de pliage est utilisée pour calculer la longueur de l'axe neutre d'un pliage de tôle, ce qui est essentiel pour déterminer la longueur correcte du modèle plat avant que le métal ne soit plié. Ce calcul garantit que les dimensions finales de la pièce pliée correspondent aux spécifications de la conception.
La formule prend en compte plusieurs paramètres clés :
La formule générale de la marge de flexion (BA) est la suivante :
Cette formule permet de calculer la longueur exacte de matériau nécessaire pour former un pli, en veillant à ce que le matériau ne s'étire pas excessivement et ne se comprime pas trop. Cette marge de pliage calculée est ensuite ajoutée aux longueurs des pattes de la pièce afin de développer un modèle plat précis, ce qui est essentiel pour produire des pièces aux dimensions précises.
La formule de la surépaisseur de pliage est également liée à la déduction de pliage, qui est la longueur à soustraire de la longueur totale de la tôle pour obtenir un motif plat correct. La déduction de pliage est calculée à l'aide de la surépaisseur de pliage et du retrait extérieur, ce qui garantit que les dimensions finales de la pièce sont exactes après le pliage.
Par exemple, si vous pliez une tôle d'acier inoxydable de 2 mm d'épaisseur à un angle de 90° avec un rayon de courbure intérieur de 3 mm et un facteur K de 0,44, la surépaisseur de pliage peut être calculée comme suit :
Cette surépaisseur de pliage est ensuite utilisée pour s'assurer que le modèle plat est correctement développé, ce qui permet d'obtenir une pièce conforme aux spécifications de conception. En résumé, la formule de surépaisseur de pliage est essentielle à la précision de la fabrication de la tôle, car elle garantit que les pièces finales sont produites aux bonnes dimensions.
Pour calculer la surépaisseur de pliage dans la tôle, il faut déterminer plusieurs paramètres clés : l'épaisseur du matériau (T), l'angle de pliage (θ), le rayon intérieur (r) et le facteur K (K). La surépaisseur de pliage (BA) est calculée à l'aide de la formule suivante :
Voici la marche à suivre, étape par étape :
En utilisant cette formule, pour les mêmes paramètres :
En suivant ces étapes et en utilisant la formule appropriée, vous pouvez calculer avec précision la surépaisseur de pliage pour vos pièces de tôle, garantissant ainsi une fabrication précise.
Le facteur K est important dans la formule de la surépaisseur de pliage pour plusieurs raisons, chacune soulignant son importance dans la fabrication de tôles de précision. Tout d'abord, il représente le rapport entre l'axe neutre et l'épaisseur du matériau. Pendant le pliage, l'axe neutre se déplace de son emplacement d'origine à 50% de l'épaisseur du matériau vers la surface intérieure du pli. Ce déplacement est critique car il détermine l'ampleur de l'allongement qui se produit dans le matériau. Le facteur K aide à calculer ce nouvel emplacement, ce qui est essentiel pour des calculs de pliage précis.
Deuxièmement, le facteur K est fondamental pour le calcul de la surépaisseur de pliage, qui est la longueur de la fibre neutre du début à la fin de l'arc généré par le pliage. Ce calcul est nécessaire pour déterminer la taille plate de la tôle requise pour obtenir la forme de pliage souhaitée. La surépaisseur de pliage est directement influencée par le facteur K, qui tient compte de l'allongement du matériau pendant le processus de pliage.
En outre, l'utilisation du facteur K permet de calculer avec précision les déductions de pliage, les retraits extérieurs et la disposition plane globale de la pièce. Cette précision est essentielle car elle garantit que les dimensions finales de la pièce pliée correspondent aux spécifications de la conception, en évitant les erreurs qui pourraient résulter de l'utilisation de valeurs génériques ou inexactes du facteur K.
Le facteur K varie en fonction de plusieurs paramètres, notamment le type de matériau, l'épaisseur, la méthode de formage, l'outillage et l'angle de pliage. Cette variabilité signifie que le facteur K doit être adapté aux conditions spécifiques du processus de pliage. En tenant compte de ces facteurs, le facteur K aide à personnaliser la formule de compensation du cintrage pour obtenir des résultats plus précis.
Enfin, une valeur correcte du facteur K est essentielle pour éviter les erreurs dans les dimensions finales de la feuille pliée. Des valeurs incorrectes du facteur K peuvent entraîner des imprécisions dans les surépaisseurs de pliage, ce qui se traduit par des pièces qui ne répondent pas aux spécifications requises. Il est donc essentiel de déterminer et d'utiliser avec précision le facteur K pour produire des composants de haute qualité.
En résumé, le facteur K est important car il permet de calculer avec précision les surépaisseurs de pliage, de tenir compte du déplacement de l'axe neutre et de prendre en considération les paramètres spécifiques du matériau et du processus, autant d'éléments essentiels pour obtenir des résultats précis et fiables en matière de pliage de tôles.
La formule de la surépaisseur de pliage dans le pliage des tôles comprend généralement plusieurs variables clés :
La marge de pliage (BA) peut être calculée à l'aide de la formule suivante :
ou
où (0,017453) est (π/180) et (0,0078) est (π /180) x K) - facteur.
Ces variables sont essentielles pour déterminer avec précision la surépaisseur de pliage, ce qui est primordial pour une fabrication précise de la tôle.
Oui, la formule de la surépaisseur de pliage peut varier considérablement en fonction du type de matériau, ainsi que d'autres facteurs tels que l'épaisseur du matériau, l'angle de pliage et le processus de pliage spécifique.
Le facteur K, élément essentiel de la formule de surépaisseur de pliage, représente le déplacement de l'axe neutre théorique pendant le pliage et varie en fonction du matériau. Par exemple, l'acier doux laminé à froid utilise généralement un facteur K d'environ 0,446, alors que d'autres matériaux comme l'acier inoxydable et l'aluminium ont des facteurs K différents en raison de leurs propriétés et comportements de flexion uniques.
La formule de la surépaisseur de pliage tient également compte de l'épaisseur du matériau et de l'angle de pliage, qui peuvent varier d'un matériau à l'autre. Une forme générale de la formule de la surépaisseur de pliage est la suivante :
où :
Les différents matériaux ont des propriétés distinctes, telles que l'élasticité, la résistance à la traction et le sens du grain, qui influencent leur comportement en matière de flexion. Par exemple, l'aluminium se plie plus facilement que l'acier, ce qui nécessite des ajustements dans le calcul de la tolérance de pliage. En outre, le pliage d'un métal dans le sens du grain peut nécessiter une force plus importante et une surépaisseur de pliage différente par rapport à un pliage dans le sens du grain.
La tendance du matériau à revenir en arrière après la flexion, connue sous le nom de retour élastique, doit également être prise en compte. Il s'agit de surplier légèrement le matériau pour tenir compte de la reprise élastique, influencée par le type de matériau et ses propriétés.
En résumé, la formule de surépaisseur de pliage doit être adaptée au matériau spécifique utilisé, en tenant compte de ses propriétés uniques, de son épaisseur et du processus de pliage impliqué.
En tant que fondateur de MachineMFG, j'ai consacré plus d'une décennie de ma carrière à l'industrie métallurgique. Ma vaste expérience m'a permis de devenir un expert dans les domaines de la fabrication de tôles, de l'usinage, de l'ingénierie mécanique et des machines-outils pour les métaux. Je suis constamment en train de réfléchir, de lire et d'écrire sur ces sujets, m'efforçant constamment de rester à la pointe de mon domaine. Laissez mes connaissances et mon expertise être un atout pour votre entreprise.
FR 
EN 
AR 
DE 
ES 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO