Comment les ingénieurs assurent-ils la résistance et la durabilité des poutres sous diverses charges ? Cet article examine les principes de la contrainte de cisaillement par flexion et les conditions nécessaires pour maintenir la résistance des poutres. Il traite de la distribution des contraintes dans différentes sections de poutres - rectangulaires, circulaires, en forme de I et annulaires à parois minces - tout en suggérant des moyens d'améliorer les performances des poutres grâce à une meilleure conception et à une meilleure utilisation des matériaux. Apprenez comment les contraintes de cisaillement et de flexion interagissent et découvrez des conseils pratiques pour optimiser la construction et l'application des poutres.
La section transversale d'une poutre soumise à une force transversale est soumise à la fois à un moment de flexion et à une force de cisaillement, ce qui se traduit par une contrainte normale et une contrainte de cisaillement sur la section transversale. La contrainte de cisaillement en flexion de plusieurs sections de poutres courantes sera examinée ci-après.
Un petit segment d'une longueur de dx est coupé de la poutre soumise à une force de flexion transversale. La poutre n'est pas chargée et les forces de cisaillement sur les deux côtés du segment sont égales mais dans des directions opposées. Le moment de flexion à la section droite est plus important que celui à la section gauche, ce qui entraîne des contraintes normales différentes sur les deux sections.
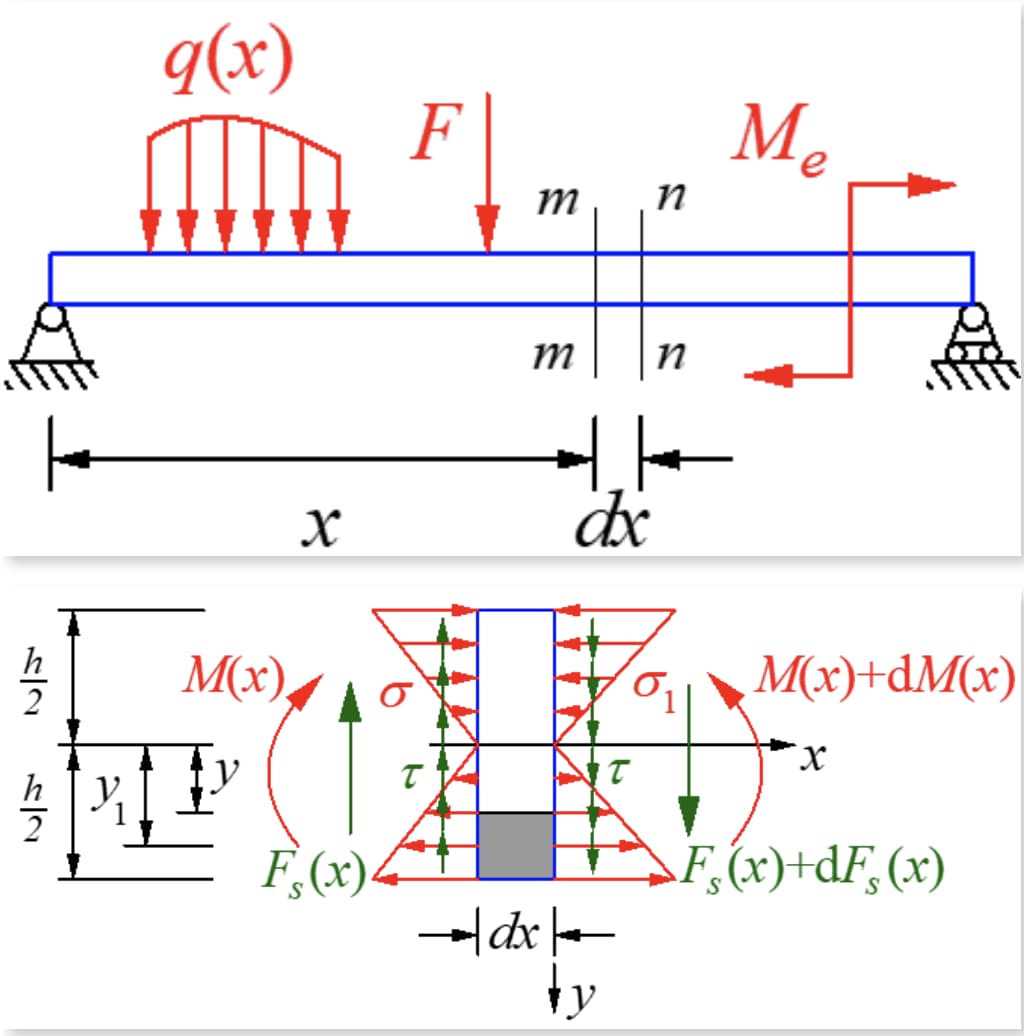
Pour une section rectangulaire étroite, la contrainte de cisaillement est tangente à la limite des deux côtés de la poutre en raison de l'absence de contrainte de cisaillement sur le côté. Cela signifie que, comme la poutre est pliée symétriquement et parallèle à la limite, la contrainte de cisaillement sur l'axe y de l'axe de symétrie doit être dans la direction y et change peu le long de la direction de la largeur.
Par conséquent, les hypothèses suivantes sont formulées concernant la loi de distribution de la contrainte de cisaillement sur la section transversale :
Lorsque le rapport hauteur/largeur de la section est supérieur à 2, la solution basée sur l'hypothèse ci-dessus est suffisamment précise par rapport à la solution exacte de la théorie élastique.
Selon le théorème de réciprocité des contraintes de cisaillement, il devrait y avoir une contrainte de cisaillement égale à la taille de la section transversale sur la section longitudinale perpendiculaire à la section transversale. Coupez un micro segment le long du plan longitudinal avec l'axe neutre du moment opposé à y, et prenez le micro élément sur le côté inférieur du plan longitudinal. Les forces sont indiquées dans la figure ci-dessous.
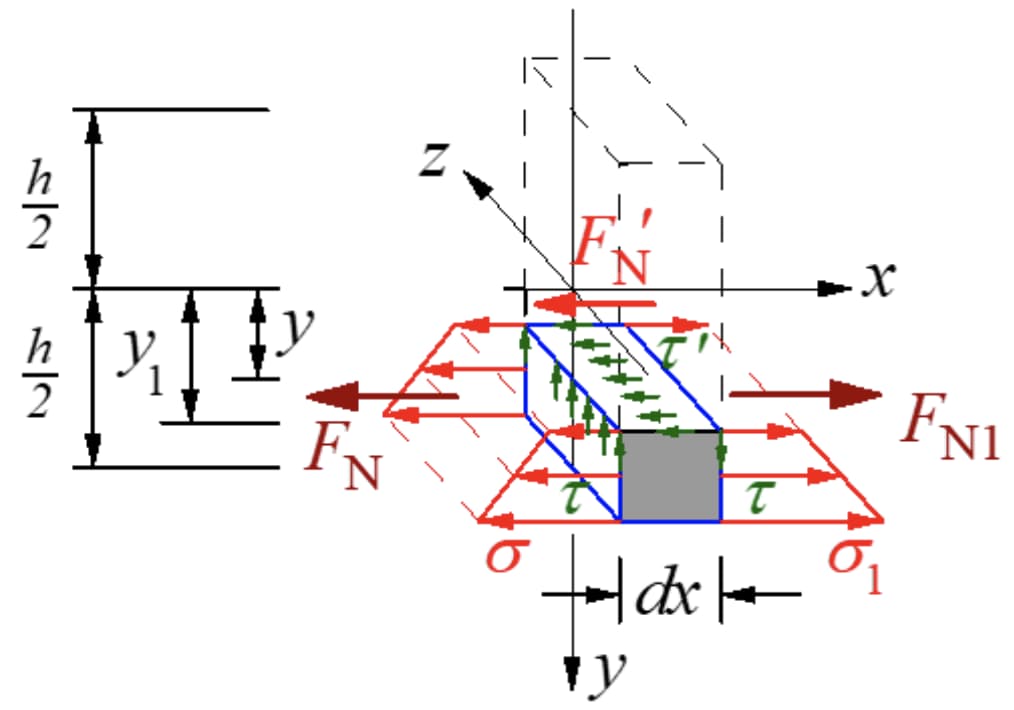
La force résultante de la contrainte normale sur la section gauche est :
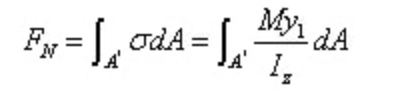
La force résultante de la contrainte normale sur la section droite est：
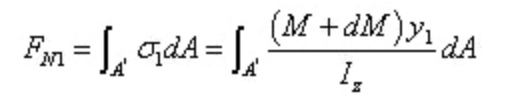
Il est clair que les deux résultantes sont de tailles différentes. Une force dans la direction axiale doit exister sur la section longitudinale pour maintenir l'équilibre du micro segment. Cette force est le résultat d'une contrainte de cisaillement, ce qui confirme la présence d'une contrainte de cisaillement sur la section longitudinale.
Comme dx est faible, la contrainte de cisaillement sur le plan longitudinal est uniformément répartie：
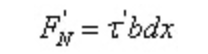
Selon les conditions d'équilibre：
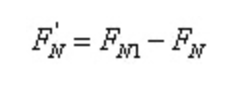
C'est-à-dire,
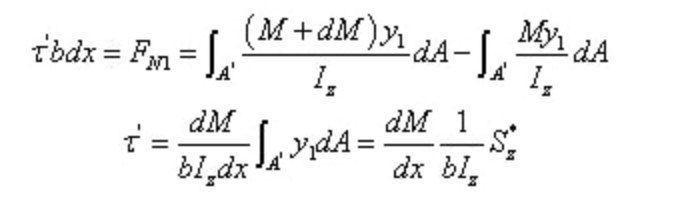
Entre autres,
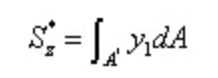
D'après le théorème de réciprocité de la contrainte de cisaillement et la relation différentielle entre la force de cisaillement et le moment de flexion :
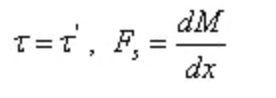
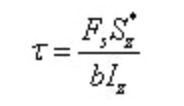
Dont :
Entre autres,
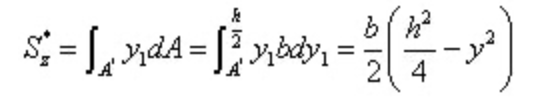
Substituer à la formule de calcul de la contrainte de cisaillement
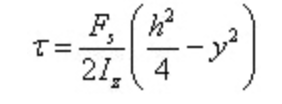
La contrainte de cisaillement est répartie en parabole le long de la hauteur de la section.
Lorsque y=0, l'effort de cisaillement est maximal sur la section au niveau de l'axe neutre
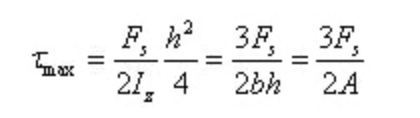
La déformation angulaire est
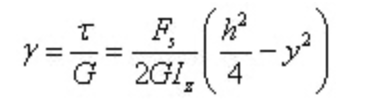
On constate que la déformation angulaire est également répartie en parabole le long de la hauteur de la section.
À ce stade, la forme de déformation de la section transversale lors de la flexion de la force transversale est illustrée dans la figure ci-dessous, ce qui prouve que la déformation de la flexion de la force transversale ne satisfait pas à l'hypothèse plane.
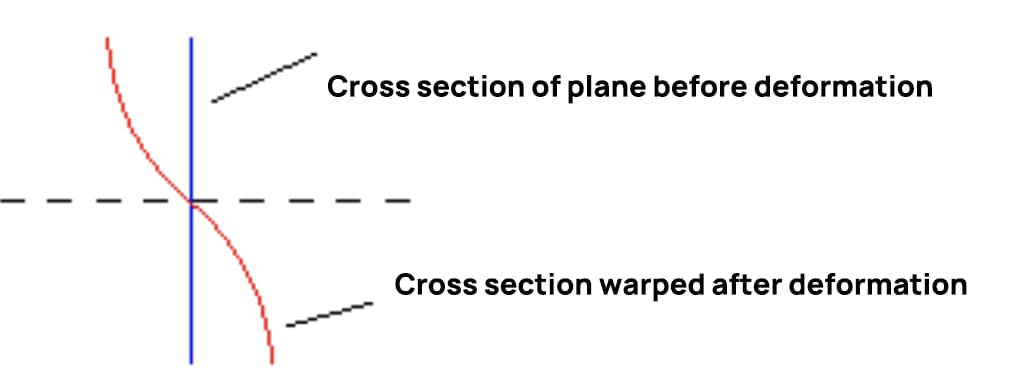
Lorsque la force de cisaillement reste constante, la contrainte de cisaillement sur les sections transversales consécutives est égale et le degré de gauchissement est également égal. La longueur des fibres longitudinales ne change pas en raison du gauchissement de la section, de sorte qu'il n'en résulte pas de contrainte normale supplémentaire. Si la force de cisaillement change avec la position de la section, le degré de déformation sur deux sections consécutives sera différent, ce qui entraînera une contrainte normale supplémentaire sur la section.
Pour les sections symétriques d'autres formes, la solution approximative de la contrainte de cisaillement peut être dérivée en utilisant la méthode ci-dessus.
Pour une section rectangulaire, dans la formule de calcul des contraintes, la largeur de la section (b) est constante, et le moment statique de la moitié de la surface de la section transversale d'un côté de l'axe neutre par rapport à l'axe neutre est le plus important. Par conséquent, la contrainte de cisaillement en chaque point de l'axe neutre est la plus importante.
Pour les sections symétriques d'autres formes, la contrainte de cisaillement maximale sur la section transversale est généralement située en divers points de l'axe neutre, à l'exception des sections dont la largeur à l'axe neutre est considérablement accrue (telles que les sections transversales) ou de certaines sections de largeur variable (telles que les sections de triangles isocèles).
Par conséquent, pour les poutres en forme de I, les poutres annulaires et les poutres à section circulaire, la contrainte de cisaillement maximale en chaque point de l'axe neutre sera principalement examinée ci-dessous.
La contrainte de cisaillement en chaque point du bord d'une section circulaire est tangente à la circonférence, selon le théorème réciproque de la contrainte de cisaillement. En chaque point de l'axe de symétrie, la contrainte de cisaillement doit être dans la direction y. On peut supposer que la distribution de la contrainte de cisaillement converge en un point de l'axe de symétrie pour chaque point de la largeur y à partir de l'axe neutre, et que les composantes de la contrainte de cisaillement le long de la direction Y en chaque point de la largeur sont égales.
La contrainte de cisaillement maximale de la section circulaire est toujours sur l'axe neutre, et sa direction est parallèle à la force extérieure, avec la même valeur en chaque point de l'axe neutre.
La contrainte de cisaillement maximale est
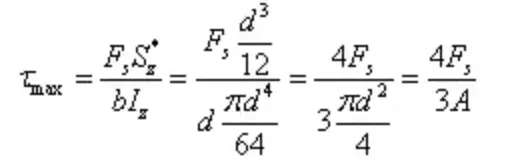
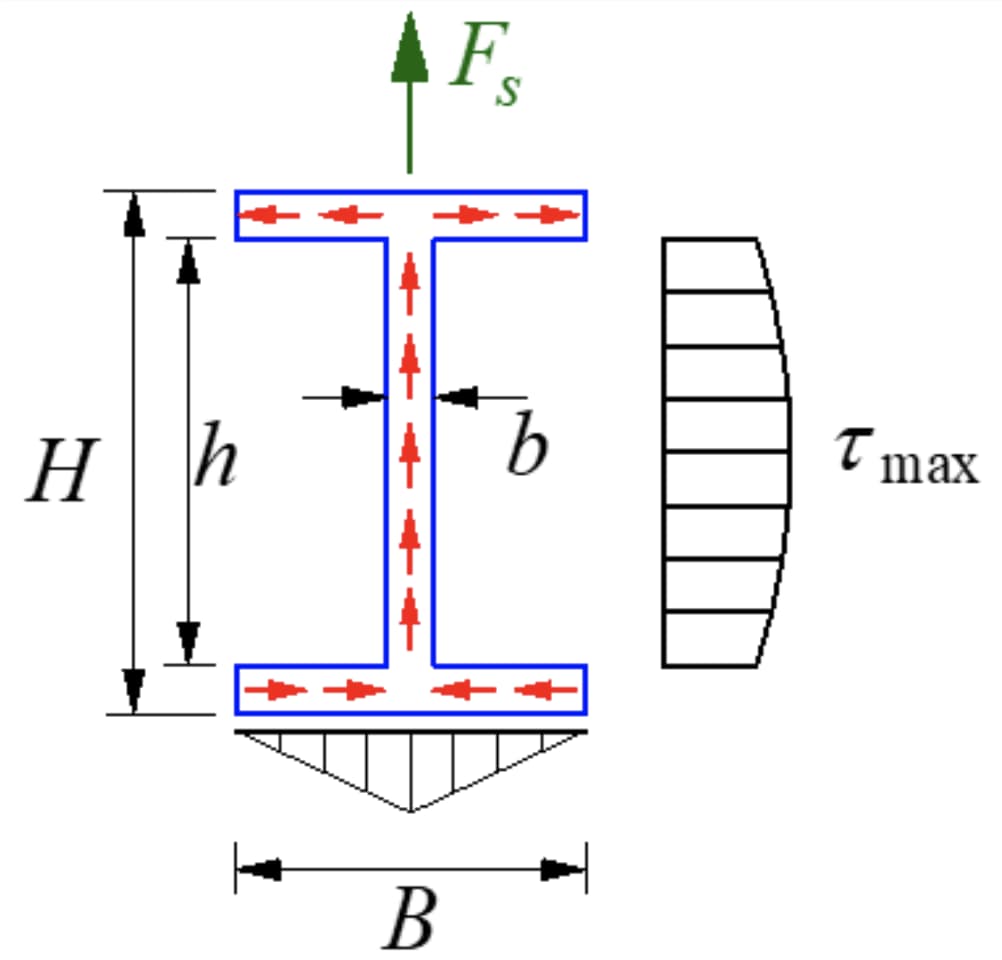
La section en forme de I est une section ouverte à parois minces dont la distribution des contraintes est illustrée par la figure. L'ampleur de la contrainte de cisaillement le long de l'épaisseur de la paroi est égale, connue sous le nom de flux de contrainte de cisaillement, s'écoulant dans la direction du cisaillement.
La composante de la contrainte de cisaillement parallèle à l'axe y sur la bride est secondaire et négligeable, l'accent étant mis sur la composante parallèle au côté long de la bride. La contrainte de cisaillement sur l'âme a une distribution parabolique, dont la taille est indiquée sur la figure.
La contrainte de cisaillement maximale se situe au niveau de l'axe neutre.
En cas de Acier en forme de Ila contrainte de cisaillement maximale :
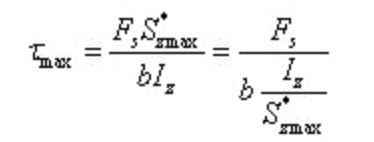
Où b est l'épaisseur de la bande et Iz/s*zmax peut être obtenu en se référant au tableau des profils en acier.
S'il s'agit d'une section en forme de I composée de trois rectangles longs et étroits, les contraintes de cisaillement maximales et minimales sur l'âme peuvent être obtenues comme suit :
Les deux formules ci-dessus montrent que la largeur de l'âme est beaucoup plus petite que la largeur de la bride, de sorte que la contrainte de cisaillement maximale sur l'âme n'est pas très différente de la contrainte de cisaillement minimale.
On peut donc considérer que la contrainte de cisaillement sur l'âme est à peu près uniformément répartie.
La contrainte de cisaillement résultante sur l'âme représente 95-97% de la force de cisaillement totale, et la force de cisaillement sur la section transversale est principalement supportée par l'âme.
Étant donné que l'âme supporte la quasi-totalité de la force de cisaillement sur la section et que la contrainte de cisaillement sur l'âme est presque uniformément répartie, la contrainte de cisaillement maximale peut être calculée approximativement en divisant la force de cisaillement par la surface de la section transversale du pôle ventral :
Dans le même temps, l'ensemble de la zone de Poutre en I La bride est la plus éloignée de l'axe neutre, et la contrainte normale en chaque point est relativement importante, de sorte que la bride supporte la majeure partie du moment de flexion sur la section.
L'épaisseur de la section annulaire à paroi mince est d, le rayon moyen de l'anneau est r, et l'épaisseur est bien inférieure au rayon moyen, de sorte que l'on peut supposer que :
La contrainte de cisaillement sur la section transversale est égale le long de l'épaisseur de la paroi ;
La direction de la contrainte de cisaillement est tangente à la ligne centrale de la section, et la direction de l'écoulement de la contrainte de cisaillement est le long de la direction de cisaillement.
La contrainte de cisaillement maximale est située sur l'axe neutre :
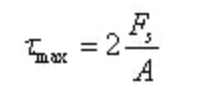
Où A est la surface de la section annulaire.
Condition de résistance à la contrainte normale de flexion :
Pour les sections neutres axisymétriques, la contrainte normale maximale de traction et la contrainte normale maximale de compression sont égales.
Les matériaux plastiques sont couramment utilisés et leurs conditions de résistance :
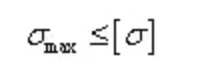
En ce qui concerne la section à axe neutre asymétrique, la contrainte normale maximale de traction et la contrainte normale maximale de compression ne sont pas égales.
Les matériaux fragiles sont couramment utilisés, ainsi que leurs conditions de résistance :
La condition de résistance de la contrainte de cisaillement par flexion est :
La contrainte normale de flexion est le principal facteur de contrôle de la poutre.
Par conséquent, la condition de résistance de la contrainte normale de flexion est souvent la base principale de la conception des poutres.
Pour améliorer la capacité portante de la poutre, deux aspects doivent être pris en compte :
D'une part, la contrainte de la poutre doit être raisonnablement arrangée pour réduire le moment de flexion maximal ;
D'autre part, une forme de section raisonnable est adoptée pour améliorer le coefficient de flexion de la section et exploiter pleinement les propriétés du matériau.
Améliorer les conditions de contrainte de la poutre et essayer de réduire le moment de flexion maximal dans la poutre.
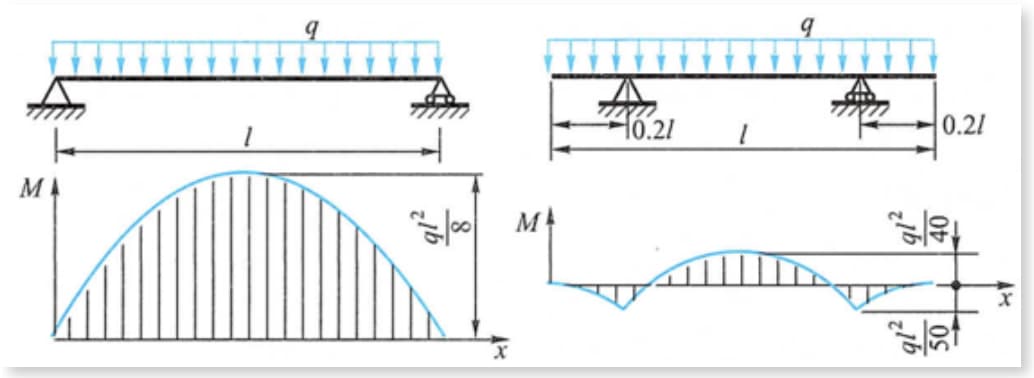
Comme le montre la figure, le moment de flexion maximal de la poutre sous une charge uniforme est fortement réduit lorsque le support est déplacé vers l'intérieur à une certaine distance des positions des deux extrémités de la poutre.
Par exemple, la poutre et le conteneur cylindrique de la grue portique, dont le point d'appui se déplace légèrement vers le milieu, peuvent réduire le moment de flexion maximal.
Plus le coefficient de flexion est élevé, plus la contrainte est faible et plus la capacité portante de la poutre est élevée.
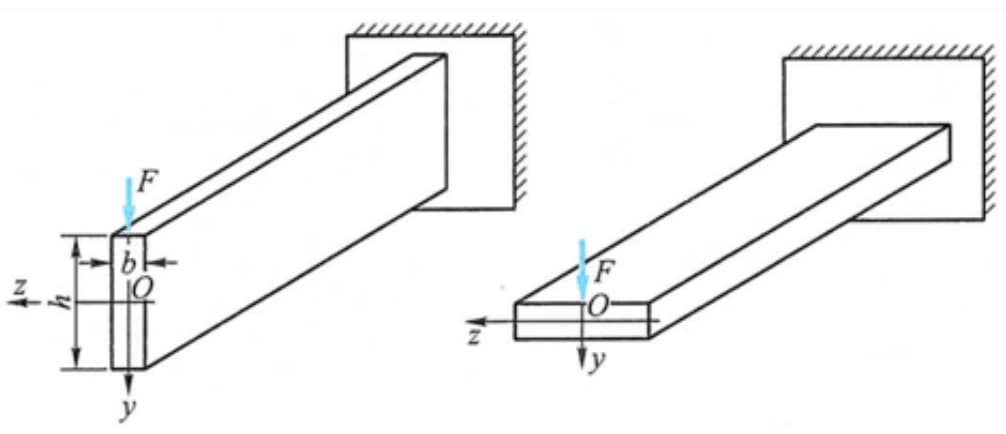
Par exemple, lorsque la poutre est chargée dans la direction verticale, le coefficient de flexion de la section est plus important lorsque la section est placée verticalement, il est donc plus raisonnable de la placer verticalement qu'horizontalement.
Tout en améliorant le coefficient de flexion de la section, nous espérons également utiliser moins de matériaux pour réaliser une meilleure économie.
Par conséquent, le rapport entre le coefficient de flexion et la surface de la section est généralement utilisé pour mesurer la rationalité de la conception de la section.
À section égale, la section rectangulaire (hauteur supérieure à la largeur) est plus raisonnable que la section circulaire, tandis que la section en forme de I ou la section en caisson est plus raisonnable que la section rectangulaire.
Par conséquent, pour utiliser pleinement les matériaux, il convient de les placer le plus loin possible de l'axe neutre.
Lors de l'examen de la forme raisonnable de la section, la propriétés mécaniques du matériau doit également être prise en compte.
Les matériaux ayant la même résistance à la traction et à la compression (comme l'acier à faible teneur en carbone) devraient adopter des sections neutres axisymétriques, comme les sections circulaires, rectangulaires, en forme de I, en caisson, etc.
De cette manière, la contrainte de traction maximale et la contrainte de compression maximale sur les bords supérieur et inférieur de la section peuvent être égales.
Pour les matériaux dont les résistances à la traction et à la compression sont inégales (comme la fonte, le ciment, etc.), il convient d'adopter la forme de section dont l'axe neutre est incliné du côté de la résistance à la traction.
Les poutres examinées ci-dessus sont toutes de section égale et le coefficient de flexion de la section est constant, mais en général, le moment de flexion de chaque section de la poutre change en fonction de la position de la section.
La conception de la section d'une poutre droite égale doit être effectuée en fonction du moment de flexion maximal, et sa contrainte maximale est proche de la contrainte admissible.
Le moment de flexion sur les autres sections est faible, la contrainte est donc faible et le matériau n'est pas pleinement utilisé.
Afin d'économiser des matériaux et de réduire le poids propre, la taille de la section peut être modifiée de manière à ce que le coefficient de section de flexion change avec le moment de flexion.
Une section plus grande est utilisée lorsque le moment de flexion est plus important, tandis qu'une section plus petite est utilisée lorsque le moment de flexion est plus faible.
Ce type de poutre dont la section change le long de l'axe est appelé poutre à section variable.
Si la contrainte normale maximale sur chaque section transversale d'une poutre à section variable est égale à la contrainte admissible, on parle de poutre à résistance égale.
En tant que fondateur de MachineMFG, j'ai consacré plus d'une décennie de ma carrière à l'industrie métallurgique. Ma vaste expérience m'a permis de devenir un expert dans les domaines de la fabrication de tôles, de l'usinage, de l'ingénierie mécanique et des machines-outils pour les métaux. Je suis constamment en train de réfléchir, de lire et d'écrire sur ces sujets, m'efforçant constamment de rester à la pointe de mon domaine. Laissez mes connaissances et mon expertise être un atout pour votre entreprise.
FR 
EN 
AR 
DE 
ES 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO