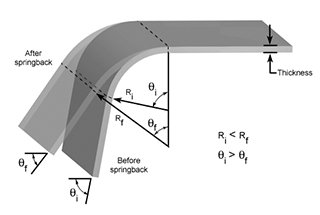
Vous êtes-vous déjà demandé pourquoi certaines pièces métalliques se ressoudent après avoir été pliées ? Dans cet article, nous allons explorer le monde fascinant des matrices de cintrage et la manière de prédire avec précision le retour élastique. Vous apprendrez des conseils pratiques et des formules pour obtenir des résultats précis dans vos projets de travail des métaux.
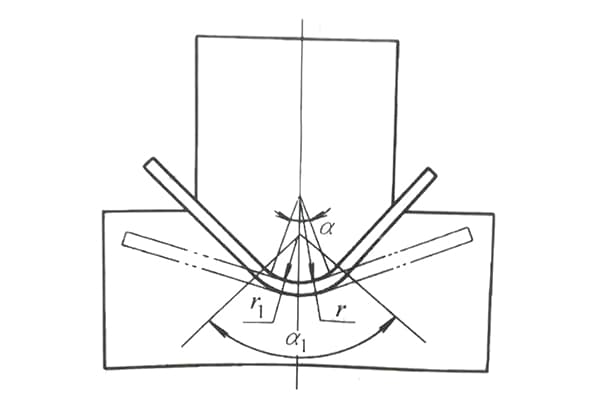
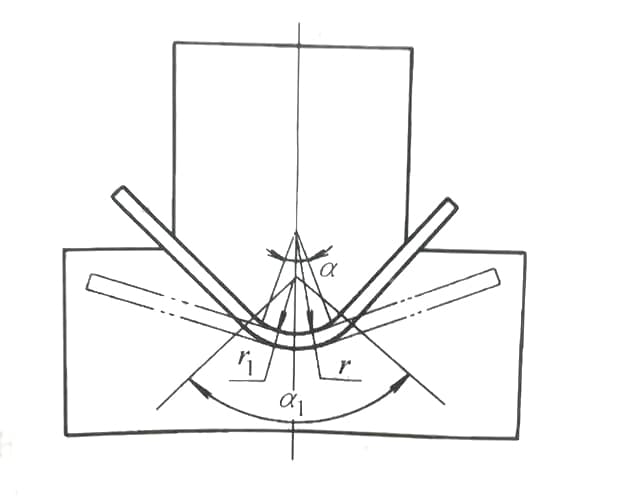
Lors de la conception d'une matrice de pliage avec un arc interne, la précision et le comportement des matériaux sont des facteurs critiques souvent négligés dans les approches conventionnelles. De nombreux concepteurs négligent totalement le retour élastique en utilisant le même rayon (R) que le produit fini ou appliquent un facteur de réduction rudimentaire à la valeur R sans tenir compte de la complexité des propriétés et des géométries des matériaux.
Par exemple, une pratique courante pour un produit dont la valeur R d'origine est de 1 mm consiste à réduire le rayon du moule convexe d'un facteur de 0,8 pour les matériaux plus durs ou de 0,9 pour les matériaux plus tendres. Cette approche simpliste, bien que parfois efficace pour des applications de base, manque de nuance pour des spécifications plus exigeantes.
Les limites de cette méthode sont particulièrement évidentes lorsqu'il s'agit de matériaux minces et de grands rayons. Prenons l'exemple d'un produit d'une épaisseur de 0,5 mm et d'un rayon interne de 200 mm. Dans ce cas, il est difficile de prédire avec précision le retour élastique en raison de l'interaction complexe entre les propriétés du matériau, le rapport épaisseur/rayon et l'angle de flexion.
Pour remédier à ces limitations et améliorer la précision de la conception des matrices, une approche plus sophistiquée est nécessaire. La section suivante présente une formule universelle de retour élastique qui tient compte de divers paramètres matériels et géométriques, ce qui permet des calculs plus précis basés sur des données numériques. Cette méthode constitue une base solide pour la conception de matrices dans une large gamme d'applications et de matériaux.
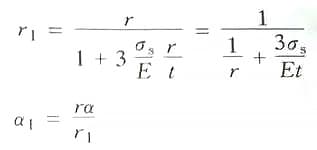
Dans la formule :
En supposant que 3σs/E=A comme coefficient de simplification, dont les valeurs sont indiquées dans le tableau 2-27. La formule de calcul du rayon de l'angle de la matrice convexe pendant la flexion des barres de section circulaire est la suivante :

La valeur de A est indiquée dans le tableau ci-dessous.
| Science des matériaux | État | A | Science des matériaux | État | A |
| 1035(L4) 8A06(L6) | recuit | 0.0012 | QBe2 | doux | 0.0064 |
| Dureté à froid | 0.0041 | dur | 0.0265 | ||
| 2A11(LY11) | doux | 0.0064 | QA15 | dur | 0.0047 |
| dur | 0.0175 | 08, 10, Q215 | 0.0032 | ||
| 2A12(LY12) | doux | 0.007 | 20, Q235 | 0.005 | |
| dur | 0.026 | 30, 35, Q255 | 0.0068 | ||
| T1, T2, T3 | doux | 0.0019 | 50 | 0.015 | |
| dur | 0.0088 | T8 | recuit | 0.0076 | |
| H62 | doux | 0.0033 | dureté à froid | ||
| mi-dur | 0.008 | ICr18N9Ti | recuit | 0.0044 | |
| dur | 0.015 | dureté à froid | 0.018 | ||
| H68 | doux | 0.0026 | 65Mn | recuit | 0.0076 |
| dur | 0.0148 | dureté à froid | 0.015 | ||
| QSn6.5-0.1 | dur | 0.015 | 60Si2MnA | recuit | 0.125 |
Si le matériel nécessaire n'est pas disponible ci-dessus, vous pouvez également vous référer au tableau ci-dessous pour trouver le matériel nécessaire. module d'élasticité et la limite d'élasticité du matériau, puis les substituer dans la formule ci-dessus pour le calcul.
| Nom du matériau | Qualité des matériaux | Statut des matériaux | La force ultime | Taux d'élongation(%) | Limite d'élasticité/MPa | Module d'élasticitéE/MPa | |
| résistant au cisaillement/MPa | traction/MPa | ||||||
| Acier de construction au carbone | 30 | Normalisé | 440-580 | 550-730 | 14 | 308 | 22000 |
| 55 | 550 | ≥670 | 14 | 390 | – | ||
| 60 | 550 | ≥700 | 13 | 410 | 208000 | ||
| 65 | 600 | ≥730 | 12 | 420 | – | ||
| 70 | 600 | ≥760 | 11 | 430 | 210000 | ||
| Acier de construction au carbone | T7~T12 T7A-T12A | Recuit | 600 | 750 | 10 | – | – |
| T8A | Trempé à froid | 600-950 | 750-1200 | – | – | – | |
| Acier au carbone de haute qualité | 10Mn2 | Recuit | 320-460 | 400-580 | 22 | 230 | 211000 |
| 65M | 600 | 750 | 18 | 400 | 211000 | ||
| Acier de construction allié | 25CrMnSiA 25CrMnSi | Recuit à basse température | 400-560 | 500-700 | 18 | 950 | – |
| 30CrMnSiA 30CrMnSi | 440-600 | 550-750 | 16 | 1450850 | – | ||
| Acier à ressort de haute qualité | 60Si2Mn 60Si2MnA 65Si2WA | Recuit à basse température | 720 | 900 | 10 | 1200 | 200000 |
| Trempé à froid | 640-960 | 800-1200 | 10 | 14001600 | – | ||
| Acier inoxydable | 1Cr13 | Recuit | 320-380 | 400-170 | 21 | 420 | 210000 |
| 2Cr13 | 320-400 | 400~500 | 20 | 450 | 210000 | ||
| 3Cr13 | 400-480 | 500~600 | 18 | 480 | 210000 | ||
| 4Cr13 | 400-480 | 500-500 | 15 | 500 | 210000 | ||
| 1Cr18Ni9 2Cr18Ni9 | Traitement thermique | 460~520 | 580-610 | 35 | 200 | 200000 | |
| Trempé à froid | 800-880 | 100-1100 | 38 | 220 | 200000 | ||
| 1Cr18Ni9Ti | Traitement thermique adouci | 430~550 | 54-700 | 40 | 240 | 200000 | |
Il est préférable d'établir une base de données des matériaux couramment utilisés et d'obtenir les paramètres physiques manquants auprès des fournisseurs. Si les paramètres du module d'élasticité et du limite d'élasticité sont corrects, le pliage et le rebond des bornes de ressort générales, des pièces d'aspect et des profilés sont plus précis.