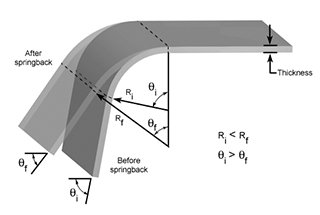
Vous êtes-vous déjà demandé comment calculer avec précision la force de flexion nécessaire à la fabrication de tôles ? Dans cet article de blog, nous allons explorer les subtilités du calcul de la force de flexion, en nous appuyant sur l'expertise d'ingénieurs mécaniciens chevronnés. Découvrez les facteurs clés qui influencent la force de flexion et apprenez à appliquer des formules éprouvées pour optimiser vos processus de formage des métaux. Préparez-vous à élever vos connaissances sur le pliage de la tôle à de nouveaux sommets !
Actuellement, les formules de calcul de la force de flexion qui sont largement utilisées ont été adoptées à partir de sources étrangères sans aucune information sur leur origine ou leur champ d'application.
Cet article présente une analyse systématique du processus de dérivation de la formule de calcul de la force de flexion, ainsi que des paramètres requis.
En outre, une nouvelle approche pour le calcul de la force de flexion est introduite afin d'élargir son champ d'application.
Le calcul de la force de pliage de la tôle est essentiel pour obtenir des processus de pliage précis et efficaces. La compréhension de ces calculs permet de sélectionner les outils appropriés et de garantir la qualité des pliages. Ce chapitre présente une vue d'ensemble des concepts clés, des outils et des conseils pratiques pour le calcul de la force de pliage dans le travail de la tôle.
Les calculs de la force de pliage sont essentiels dans le travail de la tôle pour s'assurer que la bonne quantité de force est appliquée pendant le processus de pliage. Cela permet d'éviter le gaspillage de matériau, d'endommager l'outil et de garantir la qualité de pliage souhaitée. Des calculs précis permettent de sélectionner la presse plieuse et l'outillage adéquats, ce qui se traduit par une production efficace et des économies.
La force de flexion ( F ) nécessaire pour plier une tôle peut être calculée à l'aide de la formule suivante :
où :
Le rayon interne ( R ) du coude est souvent approximé sur la base de l'ouverture de la matrice ( V ) :
L'ouverture de la filière ( V ) est choisie en fonction de l'épaisseur de la feuille ( S ) :
La longueur minimale de la bride garantit que le matériau ne tombe pas pendant le processus de pliage et est calculée en fonction de l'ouverture de la matrice et de l'angle de pliage.
Ces dernières années, la machine de presse plieuse s'est largement répandu dans diverses industries et a élargi ses capacités de traitement.
Malgré sa popularité, le calcul de la force de flexion n'a pas fait l'objet d'une discussion systématique.
Actuellement, il existe environ deux types de formules de calcul de la force de flexion recommandées par les manuels de produits des différents fabricants. fabricants de presses plieuses.
Dans la formule :
La formule recommandée par le fabricant pour calculer la force de flexion est basée sur une formule mentionnée précédemment.
Ces deux formules ont été extraites de diverses brochures de produits, mais rien ne prouve qu'elles soient exactes.
Calculatrice associée : Calculateur de tonnage pour les presses plieuses
La figure 1 est une représentation schématique de la processus de pliage d'une feuille.
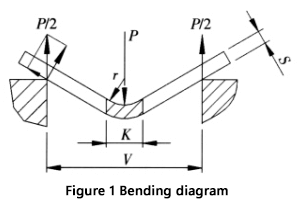
Le calcul de la force de flexion et ses paramètres sont expliqués comme suit :
La largeur recommandée de l'ouverture inférieure de la filière (V) pour le pliage libre est de 8 à 10 fois l'épaisseur de la tôle (S), avec un rapport largeur/épaisseur de V/S = 9.
Les fabricants de presses plieuses indiquent les valeurs de la largeur de la matrice (V) et du rayon intérieur (r) de la pièce pliée dans leur tableau des paramètres de la force de flexion. Le rapport rayon/largeur est généralement r = (0,16 à 0,17) V et, dans le cas présent, la valeur de 0,16 est utilisée.
Au cours du processus de pliage, le matériau dans la zone de déformation subit une déformation plastique importante qui le fait plier autour de l'axe central.
Dans certains cas, de petites fissures peuvent apparaître sur la surface extérieure de la zone incurvée.
La contrainte dans la zone de déformation, sauf à proximité de la couche centrale, est proche de la résistance à la traction du matériau, la partie supérieure de la couche neutre étant comprimée et la partie inférieure étant en tension.
La figure 2 illustre la coupe transversale et le diagramme de contrainte correspondant dans la zone de déformation.
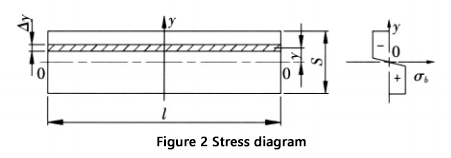
Le moment de flexion à la section de la zone de déformation est :
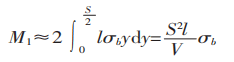
Le moment de flexion produit par la force de flexion dans la zone de déformation est représenté dans la figure 1.
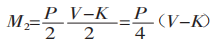
De M1 = M2nous obtenons :
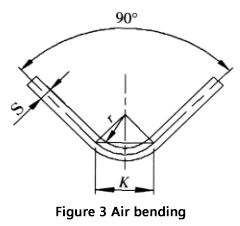
Lors du pliage d'une tôle à l'aide d'un moule universel sur une cintreuse, comme le montre la figure 3, la plupart des tôles sont pliées à 90°. Dans ce cas, K est :
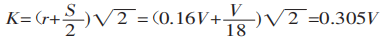
En substituant K à l'équation (1), nous obtenons :
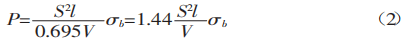
La résistance à la traction des matériaux ordinaires, σb, est de 450 N/mm². Cette valeur peut être utilisée dans la formule (2) pour calculer le résultat.
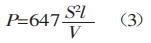
La formule de calcul de la force de flexion obtenue ici est en accord avec les informations fournies dans les brochures étrangères.
Les variables de la formule sont les suivantes
Comme le montre le processus de dérivation, lorsque l'on utilise les formules (2) ou (3) pour calculer la force de flexion, il est important de s'assurer que deux conditions supplémentaires sont remplies : le rapport entre la largeur et l'épaisseur (V/S) doit être égal à 9, et le rapport entre le rayon et la largeur doit être égal à 0,16.
Si ces conditions ne sont pas remplies, des erreurs significatives peuvent en résulter.
Le calcul de la force de flexion peut être compliqué lorsqu'il n'est pas possible de respecter les deux exigences supplémentaires (rapport largeur/épaisseur V/S = 9 et rapport rayon/largeur = 0,16) en raison de limitations liées à la conception ou au processus.
Dans de telles situations, il est conseillé de suivre les étapes suivantes :
Ces étapes permettent d'obtenir un résultat plus précis et plus fiable qu'avec la formule couramment utilisée. Un exemple illustrant ce processus est présenté à la figure 4.
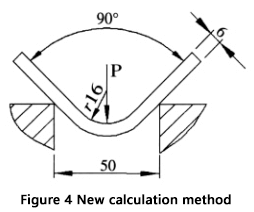
Étant donné : L'épaisseur de la tôle (S) = 6 mm, la longueur de la tôle (l) = 4 m, le rayon de courbure (r) = 16 mm, la largeur de l'ouverture de la matrice inférieure (V) = 50 mm et la résistance à la traction du matériau (σb) = 450 N/mm².
Question : Comment calculer la force de flexion nécessaire pour un cintrage pneumatique ?
Voici la marche à suivre :
Il faut d'abord calculer le rapport entre la largeur et l'épaisseur et le rapport entre le rayon et la largeur :
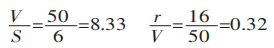
Calculez ensuite la largeur projetée de la zone de déformation :
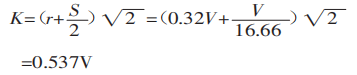
Enfin, utilisez la formule (1) pour calculer la force de flexion :
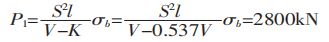
Si la formule habituellement recommandée est utilisée pour calculer la force de flexion :
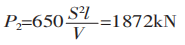
On peut déduire de P1/P2 = 1,5 que la différence entre P1 et P2 est de 1,5 fois.
La raison de cet écart est que, dans cet exemple, le rayon de courbure est relativement grand, ce qui entraîne une augmentation de la surface déformée et nécessite donc une force de courbure plus importante.
Le rapport entre le rayon et la largeur dans cet exemple est de 0,32, ce qui dépasse les critères mentionnés précédemment.
L'utilisation de la formule standard pour calculer la force de flexion n'est pas adaptée à ce scénario. Les avantages de l'utilisation de la nouvelle méthode de calcul peuvent être observés dans cet exemple.
En outre, un calculateur en ligne est disponible pour calculer la force de flexion à l'aide de la nouvelle méthode.
Tableau de résistance à la traction
| Matériau | Résistance à la traction | ||
|---|---|---|---|
| Américain | Européen | Chine | N/mm² |
| Aluminium 6061 | Alu50 | LD30 | 290 |
| Aluminium 5052 | Alu35 | LF2 | 303 |
| 1010 Acier doux | DC01 | 10/10F | 366 |
| A 536 -80 G 60-40-18 | GGG-40 | QT400-18 | 400 |
| A 351 G CF 8 | G-X 6CrNi 18 9 | Q235 | 450 |
| A 572 G50 | S 355 MC | Q345 | 550 |
| Inox 304 | Inox V2A | 0Cr18Ni9 | 586 |
| Inox 316 | Inox V4A | 0Cr17Ni12Mo2 | 600 |
| 4140 Faible alliage | 42 CrMo 4 | 42CrMo | 1000 |
Les formules de calcul des paramètres du monnayage sont différentes de celles du cintrage de l'air.
1. Largeur de la veine de la filière :
V = tôle l'épaisseur × 5
2. Le rayon interne est déterminé par la pointe du poinçon, qui doit être choisie conformément à la formule suivante :
Rayon = épaisseur de la tôle × 0.43.
3. Force requise pour le monnayage：
F(kn/m)=Épaisseur2×1,65×Résistance à la traction (N/mm2)×4,5/Largeur de l'embase
4. La formule de calcul du bord interne minimal reste la même :
Bord interne minimum = Die vee × 0.67
Certains outils nécessitent une force particulière pour céder la tôle et gérer le retour élastique afin d'obtenir le profil requis.
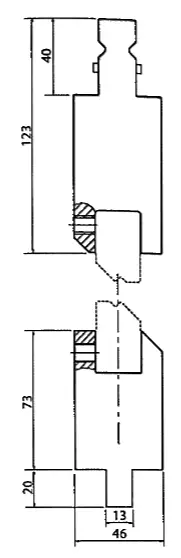
À titre d'exemple, nous considérerons les outils de jogging, qui réalisent deux courbes à la fois avec une courte distance entre la courbe et le contre-courbe.
Ces outils permettent de réaliser deux courbes à la fois, dos d'âne doit être entièrement annulé par le monnayage.
L'équation permettant de calculer la force nécessaire est la suivante :
Les outils de calage sont généralement constitués d'un support dans lequel les outils de calage, choisis en fonction du calage et de l'angle requis, sont fixés à l'aide de vis sans tête.
Il est important de demander des conseils techniques au fabricant avant d'acheter, car ces systèmes ne peuvent plier que des tôles minces, d'une épaisseur maximale de 2 mm, mais l'épaisseur maximale dépend du type d'insert et peut être inférieure à 2 mm.
Vous trouverez ci-dessous les réponses à certaines questions fréquemment posées :
La résistance à la traction joue un rôle crucial dans la détermination de la force de pliage requise pour la tôle. La résistance à la traction est la contrainte maximale qu'un matériau peut supporter lorsqu'il est étiré avant de se rompre. Lorsque la tôle est pliée, elle subit des contraintes de traction et de compression. La surface extérieure du pli est soumise à une contrainte de traction, tandis que la surface intérieure subit une contrainte de compression.
La force de flexion requise est directement influencée par la résistance à la traction du matériau, car une résistance à la traction plus élevée signifie que le matériau peut supporter une contrainte plus importante sans se rompre. Cela signifie que pour les matériaux ayant une résistance à la traction plus élevée, une force plus importante est nécessaire pour obtenir le même degré de flexion par rapport aux matériaux ayant une résistance à la traction plus faible.
Pour calculer la force de flexion, on considère la contrainte de flexion, qui est liée à la résistance à la traction. La formule de la contrainte de flexion
implique le moment de flexion (M), la distance entre l'axe neutre et la fibre la plus extérieure (c), et le moment d'inertie de la section transversale (I). Le moment de flexion est influencé par la force appliquée et la longueur du bras de levier. Il est essentiel de veiller à ce que la contrainte de flexion n'excède pas la résistance à la traction du matériau afin d'éviter toute défaillance pendant la flexion.
En résumé, une résistance à la traction plus élevée nécessite une force de flexion plus importante pour plier une tôle sans la faire céder, ce qui souligne l'importance de prendre en compte les propriétés des matériaux dans les calculs de la force de flexion.
Lors du calcul de la force de flexion de la tôle, plusieurs facteurs clés doivent être pris en compte pour garantir des résultats précis et fiables. Les principaux facteurs qui influencent les calculs de la force de flexion sont les suivants :
Les propriétés des matériaux jouent un rôle crucial, en particulier la résistance à la traction et la limite d'élasticité. La résistance à la traction est la contrainte maximale qu'un matériau peut supporter avant de céder. Par exemple, la résistance à la traction de l'aluminium est de 200 à 300 N/mm², celle de l'acier doux (Q235) de 370 à 500 N/mm² et celle de l'acier inoxydable d'environ 650 à 700 N/mm². La limite d'élasticité détermine la contrainte à laquelle le matériau commence à se déformer plastiquement, une limite d'élasticité plus élevée nécessitant une force de flexion plus importante.
L'épaisseur du matériau a un impact significatif sur la force de flexion, car les matériaux plus épais résistent davantage à la déformation, ce qui nécessite une force plus importante. Les formules de calcul incluent généralement l'épaisseur du matériau comme variable clé.
Le rayon et l'angle de cintrage sont également importants. Le rayon de courbure intérieur, ou le rayon de la courbure, influence la force nécessaire, les rayons plus petits nécessitant une force plus importante en raison d'une concentration de contraintes plus élevée. L'angle de pliage influe sur la force nécessaire, la plupart des calculs étant basés sur un pliage à 90 degrés, mais nécessitant des ajustements pour des angles différents.
La configuration de l'outillage et de la matrice, en particulier l'ouverture du canal inférieur de la matrice, affecte la force de cintrage. La largeur du canal inférieur de la matrice dans la machine de cintrage est liée à l'épaisseur du matériau, et le cintrage de précision peut nécessiter une ouverture en V plus étroite pour les matériaux plus minces.
Le facteur K et la position de l'axe neutre influencent également le processus de pliage. Le facteur K, bien qu'il soit plus directement lié au calcul des tolérances et des déductions de flexion, affecte le comportement global de la flexion et la force requise en déterminant l'endroit où le matériau n'est ni comprimé ni étiré.
Enfin, le calcul de la force de flexion implique généralement une formule qui incorpore la résistance à la traction du matériau, son épaisseur et la longueur du pli. Par exemple, une formule simplifiée pour l'acier à faible teneur en carbone est la suivante :
où ( t ) est l'épaisseur en mm et ( l ) la longueur en mètres, le résultat étant exprimé en tonnes.
En tenant compte de ces facteurs, vous pouvez calculer avec précision la force de pliage requise pour les opérations de pliage de tôles, en veillant à ce que la presse plieuse soit réglée correctement pour obtenir le pliage souhaité sans provoquer de défaillance du matériau ou de déformation excessive.
Pour déterminer les réglages appropriés d'une presse plieuse, vous devez tenir compte de plusieurs facteurs clés afin de garantir un pliage précis et efficace de la tôle. Tout d'abord, identifiez le type et l'épaisseur du matériau, car ils influencent considérablement la force de pliage requise. Les différents métaux, tels que l'acier inoxydable et l'aluminium, ont une résistance et une élasticité variables, qui influent sur la force nécessaire au pliage.
Ensuite, calculez le tonnage requis en utilisant la formule ( P=650S²L/V ), où ( P ) est la force de pliage, ( S ) l'épaisseur de la plaque de métal et ( V ) l'ouverture de la matrice inférieure. Tenez compte de la longueur et de l'angle de pliage, car les angles plus aigus nécessitent un tonnage plus élevé. Veillez à ce que le matériau soit correctement soutenu et aligné afin d'éviter les déformations et les imprécisions.
Les différentes méthodes de pliage, telles que le pliage à l'air, le pliage au fond et le pliage à la pièce, requièrent des tonnages différents, le pliage à l'air étant la méthode de base et le pliage à la pièce nécessitant environ huit fois le tonnage du pliage à l'air. Vérifiez que le tonnage ne dépasse pas la limite centrale de tonnage de la presse plieuse afin d'éviter toute surcharge et tout dommage potentiel.
Sélectionner l'outillage approprié en fonction du matériau et des exigences de pliage, en veillant à ce que l'outillage soit correctement aligné et installé. Étalonner la machine en l'inspectant et en la nettoyant, en réglant la butée arrière et en étalonnant la position et l'angle du coulisseau. Programmer la presse plieuse en fonction du tonnage et des paramètres de pliage calculés, et effectuer un essai sur un matériau de rebut pour affiner les réglages et garantir les résultats souhaités.
En suivant ces étapes, vous pouvez déterminer avec précision les réglages appropriés pour votre presse plieuse, ce qui vous permettra de réaliser des opérations de pliage de tôle précises et efficaces.
Les formules et les étapes fournies pour le calcul de la force de flexion conviennent non seulement à la flexion angulaire d'une tôle, mais aussi à la flexion en arc de cercle (qui, techniquement, devrait être appelée flexion angulaire avec un grand rayon de courbure).
Il est essentiel de garder à l'esprit que la formation d'un arc de cercle nécessite une conception unique du moule.
Lors de la projection de la zone de déformation, le calcul doit être basé sur les paramètres du processus établis au cours du processus, qui ne peuvent pas être déterminés par une formule unique.
Dans une usine de tours en fer, nous avons plié avec succès un cylindre d'une épaisseur de 12 mm, d'un diamètre de 800 mm et d'une longueur de 16 m à l'aide d'une presse de 28 000 kN. machine à freiner et un moule circulaire.
La méthode décrite dans cet article a été utilisée pour déterminer la force de flexion et a donné des résultats satisfaisants lors de la conception d'un moule pour une forme d'arc.
Pour en savoir plus :
En tant que fondateur de MachineMFG, j'ai consacré plus d'une décennie de ma carrière à l'industrie métallurgique. Ma vaste expérience m'a permis de devenir un expert dans les domaines de la fabrication de tôles, de l'usinage, de l'ingénierie mécanique et des machines-outils pour les métaux. Je suis constamment en train de réfléchir, de lire et d'écrire sur ces sujets, m'efforçant constamment de rester à la pointe de mon domaine. Laissez mes connaissances et mon expertise être un atout pour votre entreprise.
FR 
EN 
AR 
DE 
ES 
ID 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO 
TR