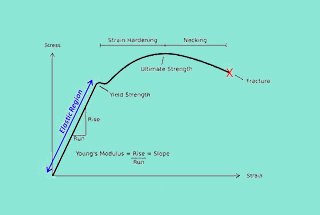
Vous êtes-vous déjà demandé comment de minuscules filets pouvaient supporter d'immenses charges ? Cet article dévoile les secrets des sections transversales des filets métriques et leur rôle dans l'ingénierie mécanique. Apprenez comment ces mesures influencent la solidité et l'efficacité de vos projets. Plongez dans cet article pour améliorer votre compréhension et stimuler vos prouesses d'ingénieur !
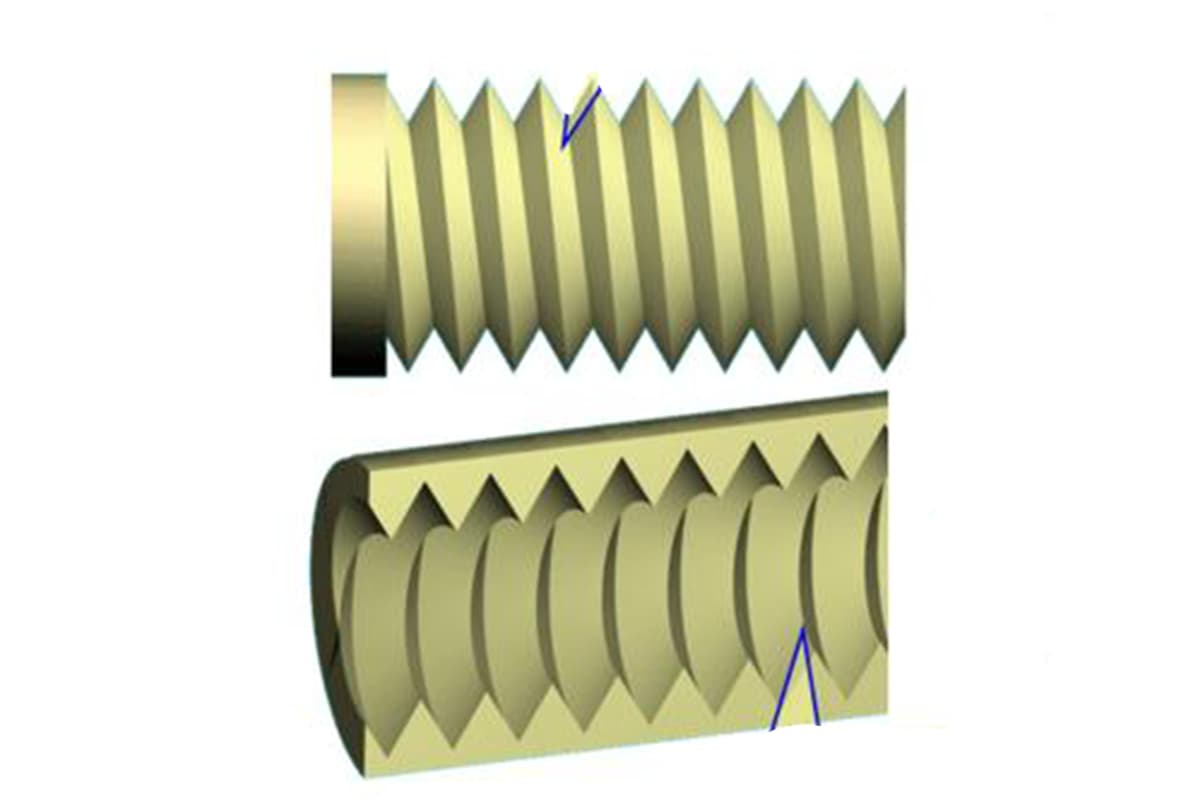
La section transversale d'un boulon est un paramètre fondamental de l'ingénierie et de la conception, car elle influence directement les propriétés mécaniques et les performances du boulon. Cette surface est essentielle pour comprendre les capacités de charge et garantir la sécurité et la fiabilité des assemblages boulonnés dans diverses applications.
La section nominale est calculée sur la base du diamètre nominal du boulon, en supposant qu'il s'agit d'une section solide, non filetée. Cette surface est souvent utilisée pour les calculs de conception initiaux.
où ( d ) est le diamètre nominal du boulon.
La zone de contrainte de traction est la section transversale effective de la partie filetée du boulon qui résiste aux charges de traction. Elle tient compte de la matière enlevée par le filetage, ce qui donne une mesure plus précise de la résistance du boulon.
Pour les filetages métriques :
Pour les filetages en pouces :
où ( d ) est le diamètre nominal et ( n ) le nombre de filets par unité de longueur.
La surface de la racine est basée sur le diamètre mineur des filets, souvent utilisé dans les applications critiques de sécurité pour une approche de conception conservatrice.
Pour les filetages métriques :
Pour les filetages en pouces :
où ( P ) est le pas de vis.
La section transversale d'un boulon est essentielle :
La section transversale d'un filet métrique est un paramètre essentiel en ingénierie mécanique, en particulier dans la conception et l'analyse des fixations. Elle détermine la capacité de charge du filet. La surface de la section transversale, souvent appelée "surface de contrainte", est la surface effective qui supporte la charge.
Vous trouverez ci-dessous un tableau reprenant les spécifications des filetages et la surface de section correspondante pour les filetages métriques standard. Les unités de diamètre sont exprimées en millimètres (mm) et les unités de section sont exprimées en millimètres carrés (mm²).
Source de la norme : GB/T16823.1-1997 Surface transversale sous contrainte et surface d'appui des fixations filetées
| Spécification du fil | Pitch (mm) | Surface transversale (mm2） |
| M1.4 | 0.3 | 0.98 |
| M1.7 | 0.35 | 1.48 |
| M2.0 | 0.4 | 2.07 |
| M2.3 | 0.4 | 2.91 |
| M2.5 | 0.45 | 3.39 |
| M3.0 | 0.5 | 5.03 |
| M3.5 | 0.6 | 6.78 |
| M4.0 | 0.7 | 8.78 |
| M4.5 | 0.75 | 11.32 |
| M5.0 | 0.8 | 14.18 |
| M6.0 | 1 | 20.12 |
| M7.0 | 1 | 28.86 |
| M8.0 | 1.25 | 36.61 |
| M9.0 | 1.25 | 48.12 |
| M10 | 1.5 | 57.99 |
| M11 | 1.5 | 72.27 |
| M12 | 1.75 | 84.27 |
| M14 | 2 | 115.44 |
| M16 | 2 | 156.67 |
| M18 | 2.5 | 192.47 |
| M20 | 2.5 | 244.79 |
| M22 | 2.5 | 303.40 |
| M24 | 3 | 352.50 |
| M27 | 3 | 459.41 |
| M30 | 3.5 | 560.59 |
| M33 | 3.5 | 693.55 |
| M36 | 4 | 816.72 |
| M39 | 4 | 975.75 |
Ce tableau constitue une référence rapide pour les ingénieurs et les concepteurs travaillant avec des filetages métriques, facilitant une conception et une analyse précises et efficaces des composants filetés.
Il est essentiel de comprendre la section transversale d'un boulon pour déterminer sa résistance et ses performances dans diverses applications techniques. Ce chapitre explore les différents types de boulons, l'importance de la surface nominale, de la contrainte de traction et de la surface de la racine, et fournit des exemples pratiques de calculs.
Il existe différents types de boulons, chacun convenant à des applications spécifiques. Les types les plus courants sont les suivants :
Le choix du type de boulon a une incidence sur le calcul de la section transversale, en particulier lorsque l'on tient compte de la contrainte de traction et des zones d'enracinement.
La surface de la section transversale d'un boulon est un facteur essentiel pour déterminer sa capacité de charge. Cette surface influence la capacité du boulon à résister aux forces de traction, de cisaillement et de compression. Des calculs précis permettent de s'assurer que le boulon peut supporter les charges prévues sans défaillance.
La section nominale suppose que le boulon est un cylindre solide sans filetage. Elle fournit une mesure de référence du diamètre du boulon. La formule pour calculer cette surface est la suivante :
où :
La zone de contrainte de traction tient compte de la matière enlevée par le filetage et est cruciale pour comprendre la résistance du boulon sous des charges de traction. Les formules de calcul de la zone de contrainte de traction sont les suivantes :
Pour les boulons de la série pouce :
Pour les boulons de la série métrique :
où :
La surface de la racine est une mesure conservatrice basée sur le diamètre mineur des filets, souvent utilisée dans les applications critiques pour la sécurité. Les formules sont les suivantes :
Pour les boulons de la série pouce :
Pour les boulons de la série métrique :
Pour un boulon d'un diamètre nominal de 0,5 pouce :
Pour un boulon de 0,5 pouce de diamètre avec 13 filets par pouce :
Pour un boulon de 12 mm de diamètre avec un pas de 1,75 mm :
Dans les applications techniques, le choix de la section transversale appropriée dépend des exigences spécifiques et des marges de sécurité. Alors que la surface nominale est utile pour les estimations initiales, la surface de contrainte de traction et la surface de racine fournissent des mesures plus précises pour les calculs de support de charge. La précision des calculs est essentielle pour la résistance et la fiabilité du boulon dans diverses applications, de la construction à la fabrication de machines.
En ingénierie et en conception, la section transversale d'un boulon est cruciale pour déterminer la performance et la sécurité des assemblages boulonnés. Cette section explore la manière dont ce paramètre est utilisé dans des scénarios réels.
Les boulons sont souvent soumis à des contraintes de cisaillement, en particulier dans les assemblages structurels tels que les joints de recouvrement où les éléments se chevauchent. La contrainte de cisaillement ((\tau)) subie par un boulon est calculée en utilisant :
où ( V ) est la force de cisaillement agissant sur le boulon et ( A_s ) la surface de la section transversale. Dans les configurations à double cisaillement, où la charge est répartie sur deux plans de cisaillement, la surface de la section transversale est prise en compte deux fois. Par exemple, si un boulon d'une section de 50 mm² est soumis à une force de cisaillement de 1000 N, la contrainte de cisaillement est la suivante :
Des calculs précis des contraintes de cisaillement permettent de s'assurer que le boulon peut supporter les charges appliquées sans se rompre.
La contrainte de traction est un autre facteur critique dans les assemblages boulonnés. La contrainte de traction ((\sigma)) est calculée en utilisant :
où ( F ) est la force de traction et ( A_t ) la surface de traction du boulon, généralement la section transversale de la partie filetée. Par exemple, si un boulon d'une surface de traction de 78,5 mm² (correspondant à un boulon M10 d'un diamètre nominal de 10 mm) est soumis à une force de traction de 2000 N, la contrainte de traction sera :
Des calculs appropriés de la contrainte de traction permettent de sélectionner des boulons capables de résister aux charges de traction prévues, ce qui évite les défaillances.
La contrainte d'appui est cruciale pour éviter les dommages locaux aux matériaux fixés par le boulon. La contrainte d'appui (Σ) est donnée par :
où ( F ) est la force, ( d_{nom} ) le diamètre nominal du boulon et ( t ) l'épaisseur du matériau. Par exemple, si un boulon d'un diamètre nominal de 12 mm fixe une plaque d'une épaisseur de 10 mm sous une force de 1 500 N, la contrainte d'appui sera :
Ce calcul permet de s'assurer que la contrainte d'appui reste inférieure à la résistance à l'appui du matériau.
Pour choisir le bon boulon, il faut tenir compte de la section transversale nécessaire pour supporter les charges prévues. Différents types de boulons et de matériaux sont utilisés en fonction des applications spécifiques. Par exemple, les boulons en acier à haute résistance peuvent être choisis pour les charpentes, tandis que les boulons en acier inoxydable sont préférés pour leur résistance à la corrosion dans les environnements marins. La section transversale permet de déterminer la capacité du boulon à résister aux contraintes.
Dans les conceptions comportant plusieurs boulons, la force totale est répartie entre eux. La force par boulon est calculée en divisant la force de l'assemblage par le nombre de boulons. Par exemple, si un assemblage requiert une force totale de 10 000 N et utilise quatre boulons, chaque boulon supportera 2 500 N. La section transversale de chaque boulon est ensuite utilisée pour déterminer la contrainte sur chaque boulon, assurant ainsi une répartition uniforme de la charge.
La précharge est la tension initiale appliquée à un boulon pendant l'installation, qui influence la rigidité de l'articulation et la répartition de la charge. La précharge garantit que les éléments de l'assemblage restent serrés et sous compression. La rigidité de l'assemblage dépend de la rigidité relative du boulon et des pièces serrées. Des boulons correctement préchargés améliorent la stabilité et la fiabilité de l'assemblage.
La conception d'assemblages boulonnés implique le respect de normes industrielles telles que l'Eurocode 3 (EN1993) et l'AISC 360-10. Ces normes fournissent des critères d'évaluation de la résistance des boulons, en incorporant des calculs impliquant la surface de la section transversale. Les facteurs de sécurité et les propriétés des matériaux sont pris en compte pour s'assurer que la connexion peut supporter les charges appliquées de manière efficace et sûre.
En résumé, la section transversale d'un boulon fait partie intégrante de diverses applications d'ingénierie et de conception. La détermination et l'application précises de ce paramètre garantissent l'intégrité structurelle et les performances des assemblages boulonnés dans différentes conditions de charge.
En tant que fondateur de MachineMFG, j'ai consacré plus d'une décennie de ma carrière à l'industrie métallurgique. Ma vaste expérience m'a permis de devenir un expert dans les domaines de la fabrication de tôles, de l'usinage, de l'ingénierie mécanique et des machines-outils pour les métaux. Je suis constamment en train de réfléchir, de lire et d'écrire sur ces sujets, m'efforçant constamment de rester à la pointe de mon domaine. Laissez mes connaissances et mon expertise être un atout pour votre entreprise.
FR 
EN 
AR 
DE 
ES 
ID 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO 
TR