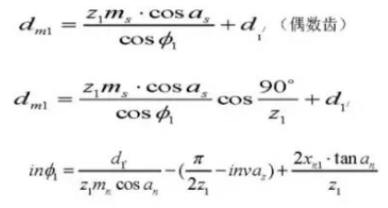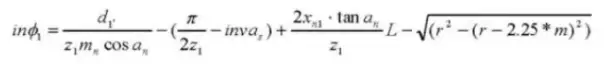Vous êtes-vous déjà interrogé sur le monde fascinant des engrenages ? Dans cet article de blog, nous allons explorer l'histoire, les types et la terminologie de ces composants mécaniques essentiels. Rejoignez-nous pour plonger dans les méandres des engrenages, guidés par l'expertise d'un ingénieur mécanicien chevronné. Découvrez l'évolution des engrenages au fil des siècles et leur rôle crucial dans les machines modernes.
Un engrenage est un composant mécanique denté de précision conçu pour s'engrener avec d'autres engrenages ou composants dentés. Il s'agit d'un élément fondamental des systèmes de transmission de puissance, qui convertit la vitesse de rotation et le couple entre les arbres. Les engrenages se caractérisent par leur forme circulaire avec des dents régulièrement espacées le long de la périphérie, suivant généralement un profil en développante pour un engrènement optimal.
L'application des engrenages dans la transmission mécanique et dans le domaine plus large de l'ingénierie mécanique est exceptionnellement diversifiée et cruciale. Ils font partie intégrante d'un large éventail de machines et d'appareils, depuis les simples outils manuels jusqu'aux équipements industriels complexes et aux véhicules à hautes performances. Les engrenages permettent un contrôle précis de la vitesse, de la direction et de la force dans les systèmes mécaniques, ce qui les rend indispensables dans les groupes motopropulseurs, les réducteurs, les différentiels et d'innombrables autres assemblages mécaniques.
La polyvalence des engrenages provient de leur capacité à être fabriqués dans différentes tailles, matériaux et configurations, y compris les engrenages droits, hélicoïdaux, coniques et à vis sans fin, chacun étant adapté à des applications spécifiques et à des exigences de performance. À mesure que la technologie progresse, la conception et la fabrication des engrenages continuent d'évoluer, intégrant de nouveaux matériaux, des techniques de production et des méthodes d'optimisation pour améliorer l'efficacité, la durabilité et la réduction du bruit dans les systèmes mécaniques.
Dès 350 avant J.-C., le célèbre philosophe grec Aristote a parlé des engrenages dans sa littérature.
Vers 250 avant J.-C., le mathématicien Archimède a également décrit dans sa littérature l'utilisation d'une turbine et d'un engrenage à vis sans fin dans un palan.
Des engrenages datant de plusieurs siècles avant Jésus-Christ sont encore conservés dans l'horloge à eau de Ktesibios, en Irak.

L'histoire des engrenages en Chine remonte à l'Antiquité et est longue et variée. Selon les archives historiques, les engrenages étaient déjà utilisés dans la Chine ancienne entre 400 et 200 avant Jésus-Christ.
Les engrenages en bronze mis au jour dans la province de Shanxi sont les plus anciens découverts à ce jour dans le monde. Les voitures guidées qui reflétaient les réalisations de la science et de la technologie anciennes étaient des dispositifs mécaniques qui tournaient autour de mécanismes d'engrenage.
Au cours de la Renaissance italienne, dans la seconde moitié du XVe siècle, le célèbre génie polyvalent Léonard de Vinci a non seulement laissé une empreinte indélébile sur les aspects culturels et artistiques, mais a également apporté des contributions significatives à l'histoire de la technologie des engrenages.
Après plus de 500 ans, les engrenages d'aujourd'hui conservent encore les esquisses des prototypes de l'époque.
(1) Engrenage droit
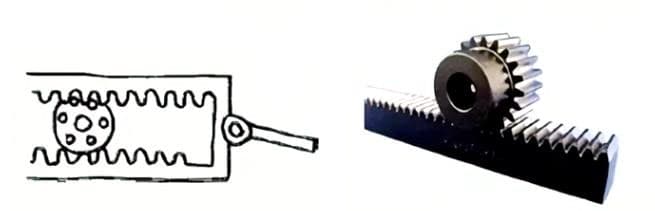
(2) Crémaillère et pignon
(3) Engrenage hélicoïdal à axes croisés

(4) Engrenage conique
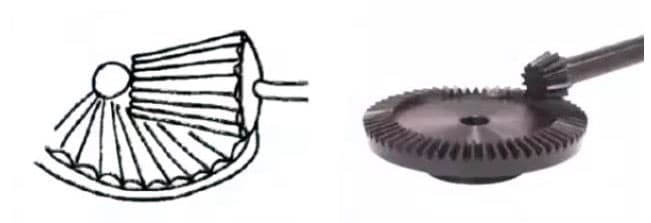
(5) Engrenage conique hypoïde à rapport de transmission élevé
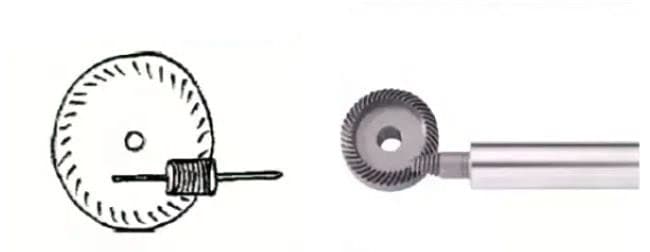
(6) Engrenage à vis sans fin
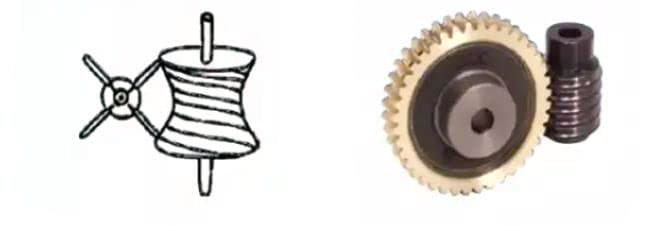
Ce n'est qu'à la fin du XVIIe siècle que l'on a commencé à étudier la forme des dents de la roue, qui permettait de transmettre le mouvement avec précision. Après la révolution industrielle en Europe au XVIIIe siècle, l'application de la transmission par engrenage s'est de plus en plus répandue.
L'engrenage cycloïdal a d'abord été développé, suivi par l'engrenage à développante. Au début du 20e siècle, l'engrenage à développante s'est imposé dans ses applications. Plus tard, des engrenages tels que l'engrenage hélicoïdal, l'engrenage à arc, l'engrenage conique et l'engrenage oblique ont été développés.
Aujourd'hui, la technologie moderne des engrenages a fait de grands progrès. Les modules d'engrenage vont de 0,004 à 100 millimètres, le diamètre de l'engrenage peut aller de 1 millimètre à 150 mètres. Les transmission de puissance La capacité de la machine peut atteindre 100 000 kilowatts et la vitesse de rotation peut atteindre 100 000 tours par minute. La vitesse circonférentielle la plus élevée peut atteindre 300 mètres par seconde.
Au niveau international, les dispositifs de transmission de puissance par engrenage évoluent vers la miniaturisation, la vitesse élevée et la normalisation. Parmi les tendances en matière de conception d'engrenages, on peut citer l'application d'engrenages spéciaux, le développement de dispositifs d'engrenages planétaires et la recherche et le développement de systèmes d'engrenages à faible vibration et à faible bruit.
Il existe différents types d'engrenages et la méthode de classification la plus courante est basée sur l'axe de l'engrenage.
En général, les engrenages sont classés en trois types : à axe parallèle, à axe croisé et à axe oblique.
Engrenages à axe parallèle : y compris les engrenages droits, les engrenages hélicoïdaux, les engrenages intérieurs, les crémaillères et les crémaillères hélicoïdales.
Iengrenages à axe croisé : y compris les engrenages coniques droits, les engrenages coniques en spirale, les engrenages coniques à zéro degré, etc.
Engrenages à axe oblique : y compris les engrenages hélicoïdaux à axes croisés, les engrenages à vis sans fin, les engrenages coniques hypoïdes, etc.
| Type de transmission par engrenage | Type d'engin | Efficacité de la transmission (%) | Représentation graphique en 3D |
Axe parallèle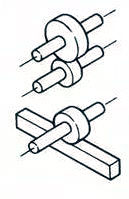 | Engrenages droits | 98.0-99.5 | 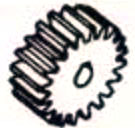 |
| Engrenages hélicoïdaux |  | ||
| Crémaillères,Crémaillères hélicoïdales |  | ||
| Engrenages internes | 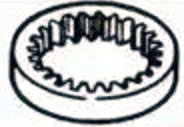 | ||
Axe d'intersection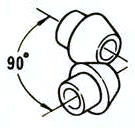 | Engrenages à onglet | 98.0-99.0 |  |
| Engrenages coniques droits |  | ||
| Engrenages coniques en spirale |  | ||
Axe oblique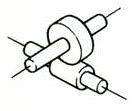 | Engrenages à vis | 70.0-95.0 |  |
| Vers | 30.0-90.0 |  | |
| Roues à vis sans fin | 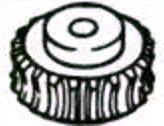 |
Le rendement indiqué dans le tableau ci-dessus est le rendement de la transmission, qui ne comprend pas les pertes dues aux roulements et à la lubrification par agitation. L'engrènement des paires d'engrenages à axe parallèle et à axe croisé se fait essentiellement par roulement, et le glissement relatif est très faible, de sorte que le rendement est élevé.
L'engrènement des paires d'engrenages à axe décalé, telles que les engrenages hélicoïdaux et les engrenages à vis sans fin, a un impact significatif sur le frottement car ils transmettent la puissance par glissement relatif, ce qui entraîne une réduction de l'efficacité de la transmission par rapport à d'autres engrenages.
Le rendement des engrenages fait référence à l'efficacité de transmission des engrenages dans leur état de montage normal.
En cas d'installation incorrecte, en particulier lorsque la distance de l'assemblage de l'engrenage conique est incorrecte et provoque une erreur à l'intersection du même biseau, son efficacité diminuera de manière significative.
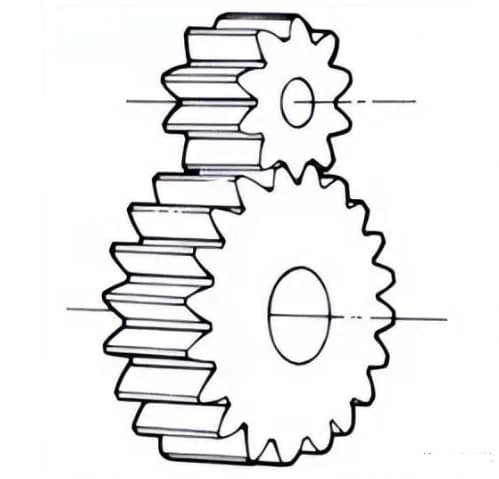
1. Engrenages droits
Engrenages cylindriques dont les lignes de dents et les lignes axiales sont parallèles. Ils sont largement utilisés dans la transmission de puissance parce qu'ils sont faciles à travailler.
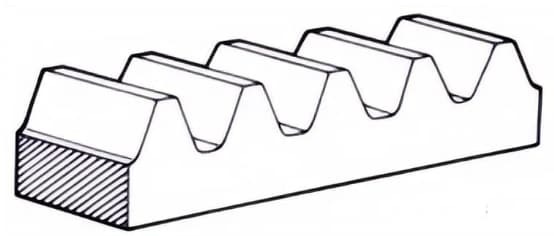
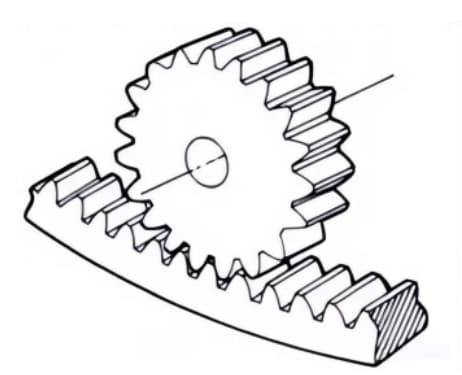
2. Support
Engrenage à denture droite qui s'engrène avec des engrenages droits. Il peut être considéré comme un cas particulier où le diamètre primitif de l'engrenage droit devient infiniment grand.
3. Engrenages internes
Engrenages dont les dents sont usinées à l'intérieur d'une bague et qui s'engrènent avec les engrenages droits. Ils sont principalement utilisés dans des applications telles que les mécanismes de transmission à engrenages planétaires et les accouplements d'engrenages.
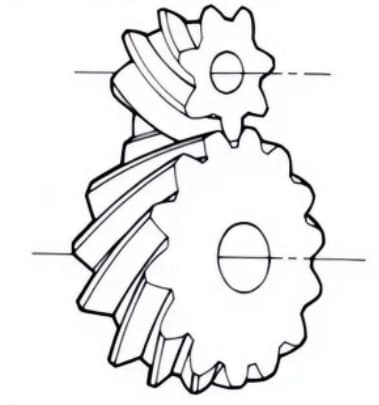
4. Engrenages hélicoïdaux
Engrenages cylindriques dont les lignes de dents sont en forme d'hélice. Ils sont largement utilisés en raison de leur grande résistance et de leur fonctionnement en douceur, par rapport aux engrenages droits. Ils génèrent une poussée axiale pendant la transmission.
5. Crémaillère hélicoïdale
Engrenage à crémaillère qui s'engrène avec des engrenages hélicoïdaux. C'est l'équivalent du cas où le diamètre primitif de l'engrenage hélicoïdal devient infiniment grand.
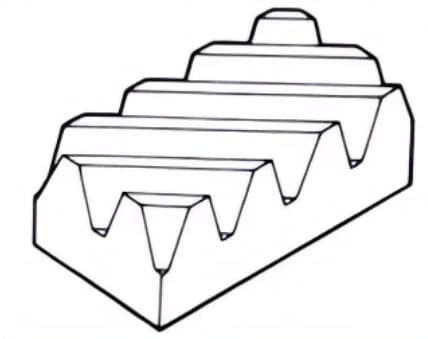
6. Engrenages à chevrons
Engrenages constitués de deux roues hélicoïdales dont les angles d'hélice sont opposés. Ils ont l'avantage de ne pas générer de poussée axiale.
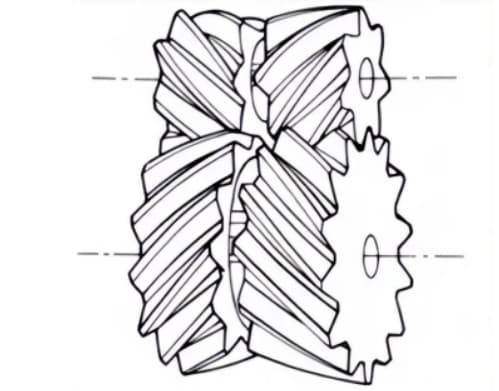
1. Engrenages coniques droits
Engrenages coniques dont les lignes de dents sont parallèles à la génératrice du cône. Ils sont relativement faciles à fabriquer par rapport à d'autres types d'engrenages coniques.
C'est pourquoi ils sont largement utilisés dans les applications d'engrenages coniques pour la transmission de puissance.
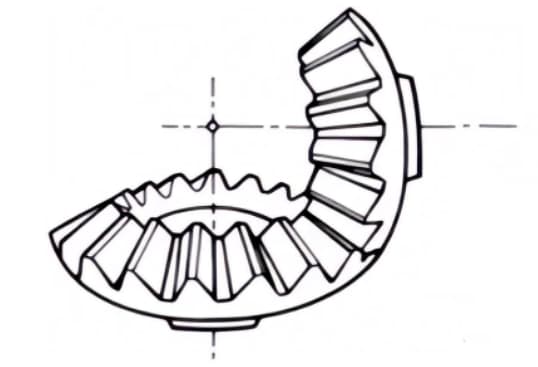
2. Engrenages coniques à spirale
Engrenages coniques dont les lignes de dents sont incurvées et qui présentent un angle d'hélice. Bien qu'ils soient plus difficiles à fabriquer que les engrenages coniques droits, ils sont largement utilisés comme engrenages à haute résistance et à faible bruit.
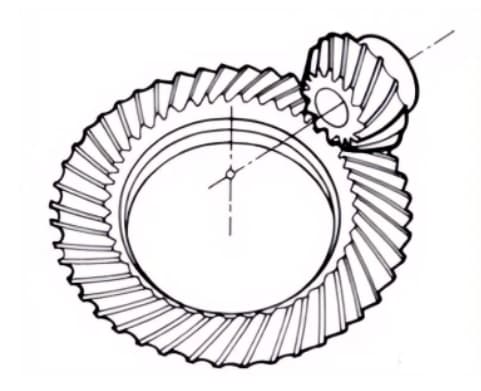
3. Engrenages coniques à zéro
Engrenages coniques courbes avec un angle d'hélice de zéro degré. Ils présentent les caractéristiques des engrenages coniques droits et hélicoïdaux, la surface de la dent étant soumise à la même situation de force que les engrenages coniques droits.
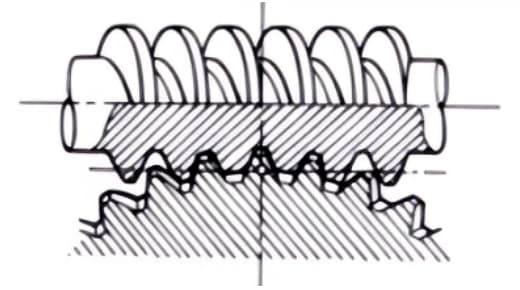
1. Paire d'engrenages à vis sans fin
Le terme "paire d'engrenages à vis sans fin" désigne la combinaison d'une vis sans fin et d'une roue à vis sans fin qui s'engrène avec elle. La principale caractéristique de la paire d'engrenages à vis sans fin est qu'elle permet d'obtenir un grand rapport de transmission avec une seule paire et qu'elle fonctionne silencieusement. Cependant, leur faible efficacité est un inconvénient.
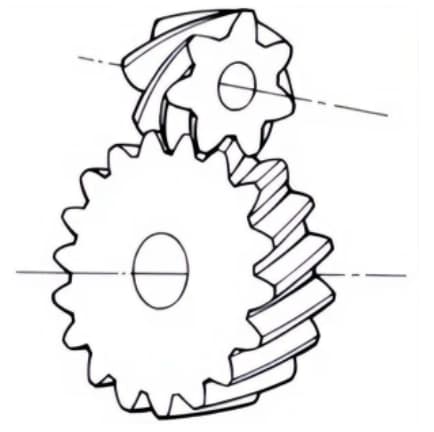
2. Paire d'engrenages hélicoïdaux et d'engrenages à vis sans fin
Terme utilisé lorsque des paires d'engrenages cylindriques à vis sans fin sont utilisées pour la transmission entre des axes décalés. Ils peuvent être utilisés dans le cas de paires d'engrenages hélicoïdaux ou entre des paires d'engrenages hélicoïdaux et des paires d'engrenages droits. Bien qu'ils fonctionnent en douceur, ils ne conviennent que pour des charges légères.
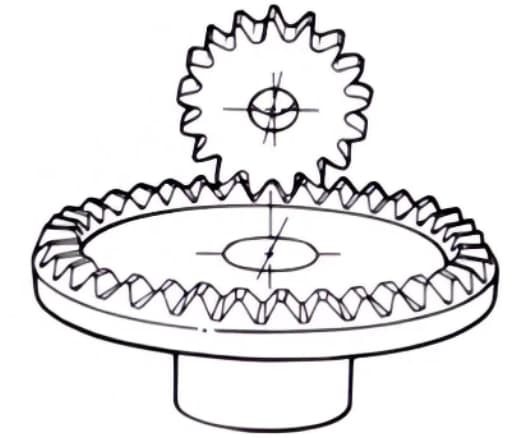
1. Engrenages de face
Engrenages en forme de disque qui peuvent s'engrener avec des engrenages droits ou des engrenages hélicoïdaux. Ils sont utilisés pour la transmission entre axes orthogonaux et axes décalés.
2. Paire d'engrenages à vis sans fin en sablier
Le terme "paire d'engrenages à vis sans fin en sablier" désigne la combinaison d'une vis sans fin en sablier et d'une roue à vis sans fin qui s'engrène avec elle. Bien qu'elles soient plus difficiles à fabriquer que les paires d'engrenages à vis sans fin cylindriques, elles peuvent transmettre de lourdes charges.
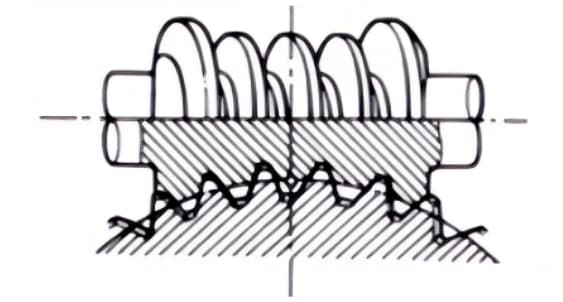
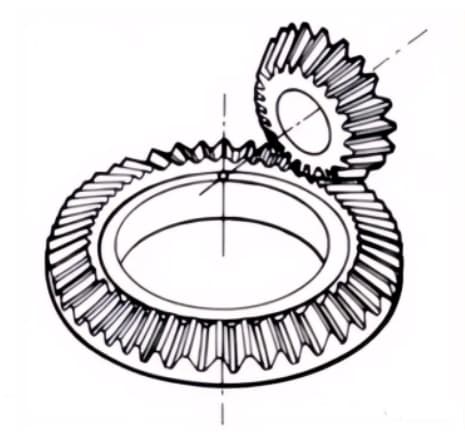
3. Engrenages hypoïdes
Engrenages coniques utilisés pour la transmission entre des axes décalés. Le plus grand et le plus petit des engrenages sont usinés de manière excentrique, comme dans le cas des engrenages coniques hélicoïdaux. Le principe d'engrènement est très complexe.
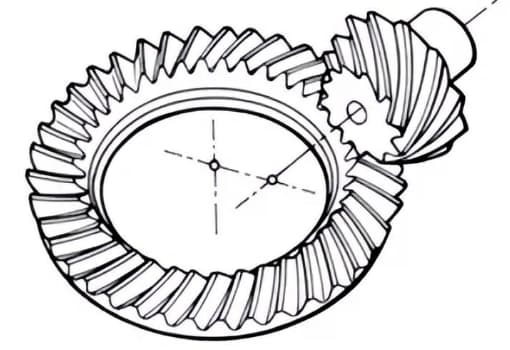
Les engrenages ont une terminologie et des méthodes de présentation qui leur sont propres. Afin d'améliorer la compréhension des engrenages, voici quelques termes de base couramment utilisés.
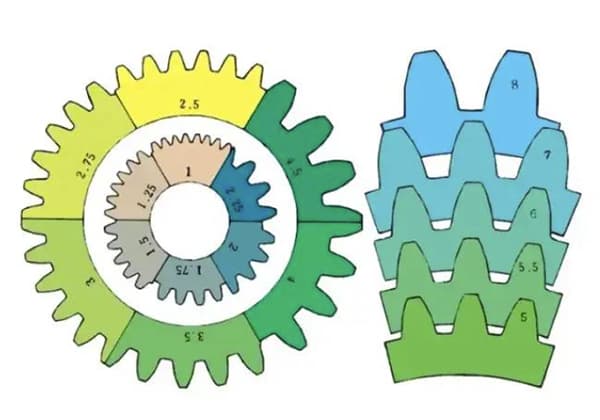
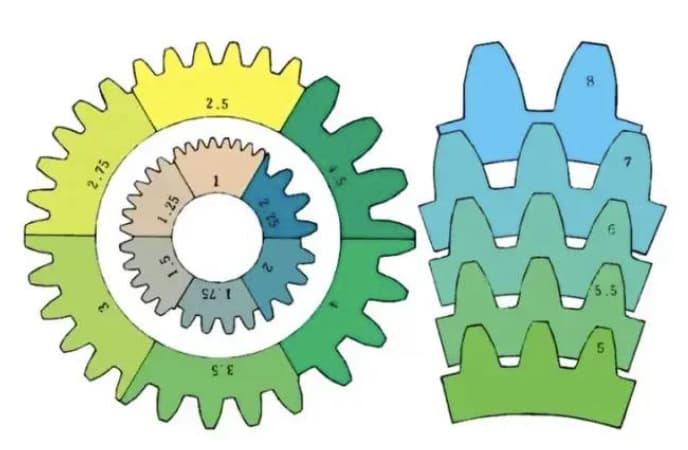
m1, m3, m8... sont respectivement appelés module 1, module 3, module 8. Le module est universellement utilisé dans le monde entier pour indiquer la taille de l'engrenage, en utilisant le symbole m (module) et des chiffres (millimètres) pour représenter la taille des dents.
Plus le nombre est élevé, plus l'engrenage est important.
Dans les pays qui utilisent les unités impériales, comme les États-Unis, la taille des dents est indiquée par le symbole DP (diametral pitch) et des chiffres (le nombre de dents pour un engrenage ayant un diamètre de pas de 1 pouce).
Par exemple : DP24, DP8, etc. Il existe également une comparaison et une méthode spéciale pour indiquer la taille des dents à l'aide du symbole CP (pas circulaire) et de chiffres (millimètres), tels que CP5, CP10.
Le pas (p) peut être obtenu en multipliant le module par pi. Le pas est la longueur entre les dents adjacentes.
La formule est la suivante : p= pi x m
Comparaison de la taille des dents pour différents modules :
L'angle de pression est un paramètre qui détermine la forme de la denture. Il se réfère à l'inclinaison de la surface de la denture et est généralement fixé à 20 degrés (α).
Auparavant, les engrenages avec un angle de pression de 14,5 degrés étaient courants.
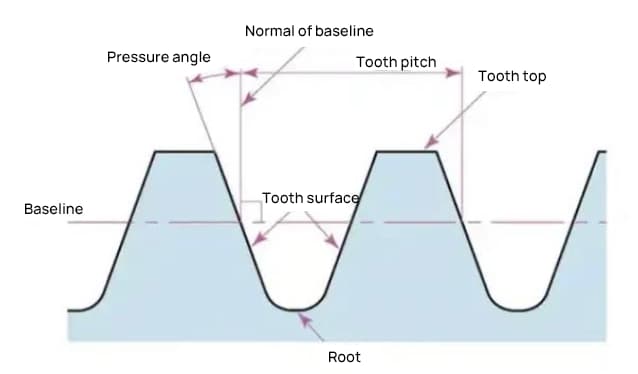
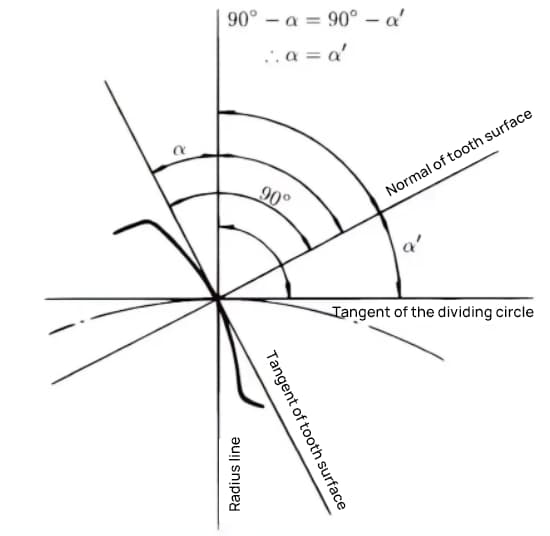
L'angle de pression est l'angle formé entre le rayon et la tangente de la forme de la dent en un point spécifique de la surface de la dent (généralement le nœud). Comme le montre l'image, α est l'angle de pression. α' est également un angle de pression puisque α' = α.
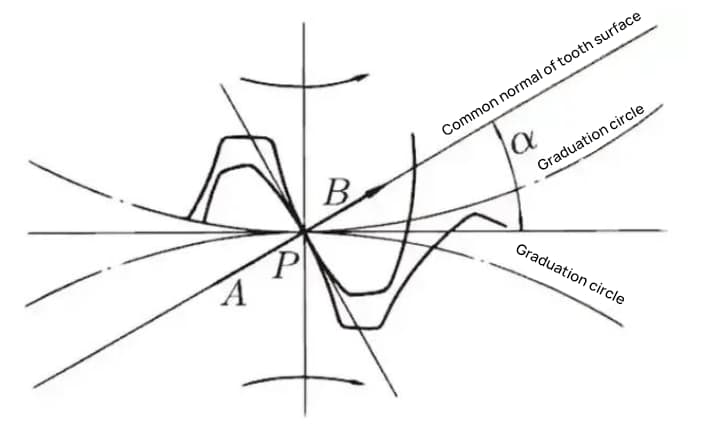
Lorsque l'état d'engrènement de l'engrenage A et de l'engrenage B est vu depuis le nœud, l'engrenage A pousse l'engrenage B depuis le nœud. À ce moment, la force motrice agit sur la normale commune de l'engrenage A et de l'engrenage B. En d'autres termes, la normale commune est la direction de la force et la direction de la pression, α étant l'angle de pression.
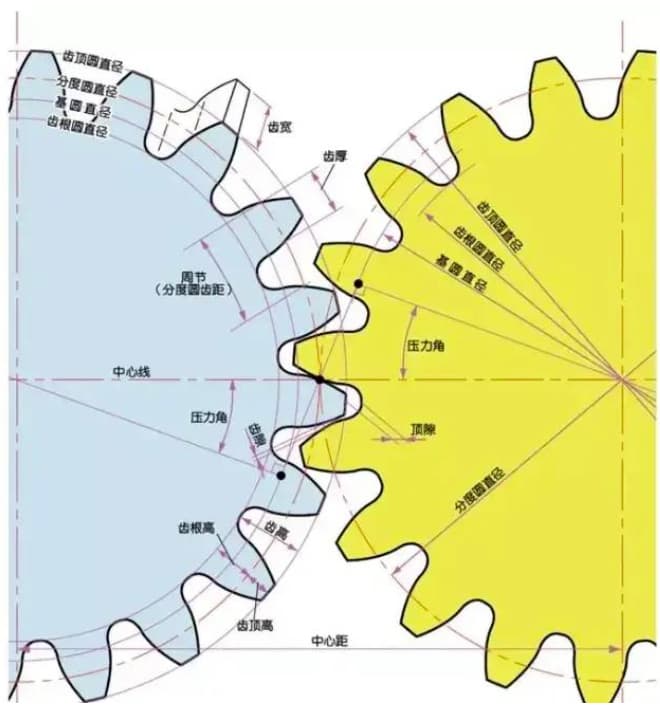
Le module (m), l'angle de pression (α) et le nombre de dents (z) sont les trois paramètres de base d'un engrenage. Sur cette base, chaque partie de l'engrenage est calculée en termes de taille.
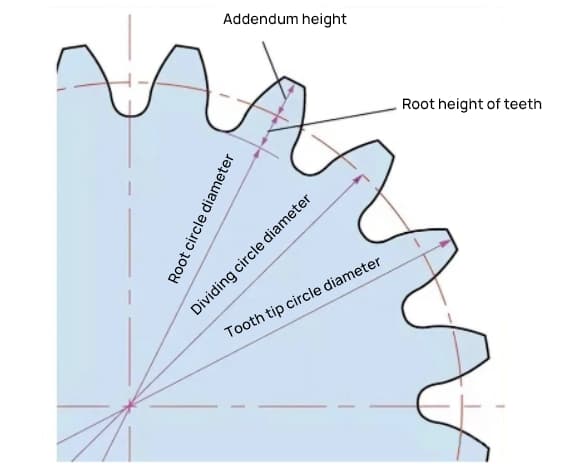
La hauteur d'une dent d'engrenage est déterminée par le module (m).
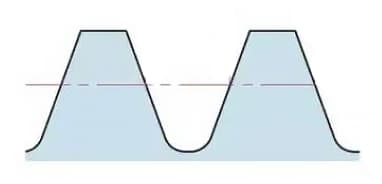
La hauteur totale de la dent est h=2,25m (= hauteur addendum + hauteur dedendum).
La hauteur de l'addendum (ha) est la hauteur entre l'extrémité de la dent de l'engrenage et le cercle primitif. ha=1m.
La hauteur du dédendum (hf) est la hauteur entre le pied de la dent de l'engrenage et le cercle primitif. hf=1,25m.
La référence pour l'épaisseur de la dent d'engrenage (s) est la moitié du pas. s=πm/2.
Le paramètre qui détermine la taille d'un engrenage est le diamètre du cercle primitif (d). Sur la base du cercle primitif, le pas, l'épaisseur, la hauteur, la hauteur additionnelle et la hauteur dédimensionnelle de l'engrenage peuvent être déterminés.
Le diamètre du cercle primitif est d=zm.
Le diamètre du cercle de l'addendum est da=d+2m.
Le diamètre du cercle de dédommagement est df=d-2,5m.
Le cercle primitif n'est pas visible directement sur l'engrenage réel car il s'agit d'un cercle supposé utilisé pour déterminer la taille de l'engrenage.
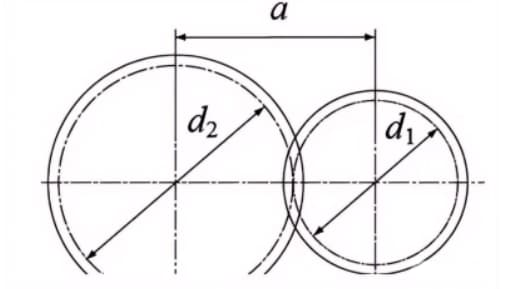
Lorsque les cercles primitifs d'une paire d'engrenages s'engrènent tangentiellement, les distance centrale est la moitié de la somme des diamètres du cercle primitif.
Entraxe a=(d1+d2)/2
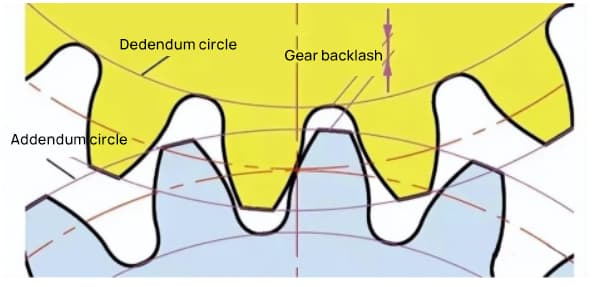
Le jeu est un facteur important pour obtenir un engrènement régulier des engrenages lors de l'engagement. Il s'agit de l'espace entre les surfaces des dents lorsqu'une paire d'engrenages est en prise.
Il existe également un jeu dans le sens de la hauteur des dents de l'engrenage. Ce jeu est appelé jeu axial ou jeu (c). Le jeu (c) est la différence entre le diamètre du cercle de pied d'un engrenage et le diamètre du cercle de tête de l'engrenage correspondant.
Dégagement c=1,25m-1m=0,25m
Un engrenage dont les dents sont torsadées en spirale après un engrenage droit est appelé engrenage hélicoïdal. La plupart des calculs géométriques effectués pour un engrenage droit sont applicables à un engrenage hélicoïdal. Il existe deux types d'engrenages hélicoïdaux en fonction de leurs surfaces de référence :
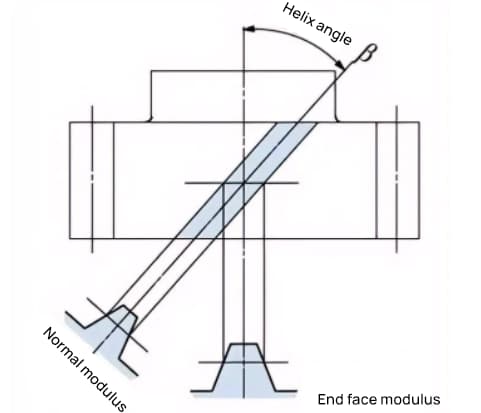
Pour les engrenages hélicoïdaux, tels que les engrenages à denture hélicoïdale et cycloïdale, dont les dents ont une forme hélicoïdale, la direction de l'hélice et l'engrènement sont fixes.
La direction de l'hélice se réfère à l'axe de l'engrenage qui pointe vers le haut et vers le bas, la direction des dents est en haut à droite (droite) et en haut à gauche (gauche) lorsque l'on regarde de l'avant. L'engrènement de différents types d'engrenages est illustré ci-dessous.

Si des dents à espacement égal sont seulement réparties sur la périphérie extérieure de la roue de frottement, munies de saillies, puis engrenées et mises en rotation les unes avec les autres, les problèmes suivants peuvent se poser :
Lorsque la transmission doit être à la fois silencieuse et souple, on utilise des courbes en développante.
Une courbe en développante est une courbe obtenue en enroulant un fil avec un crayon sur la périphérie extérieure d'un cylindre et en relâchant progressivement le fil à l'état tendu.
La courbe tracée par le crayon est la développante, et la périphérie extérieure du cylindre est appelée cercle de base.
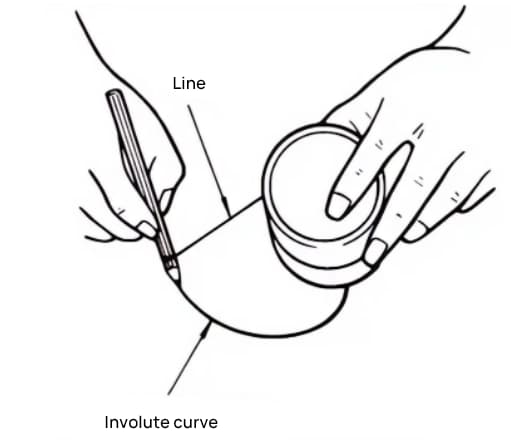
Divisez le cylindre en 8 parties égales et attachez-y 8 crayons pour tracer 8 courbes en développante. Enroulez ensuite les fils dans le sens inverse et tracez 8 autres courbes en utilisant la même méthode. Il s'agit d'un engrenage à 8 dents dont le profil de la denture est en développante de cercle.
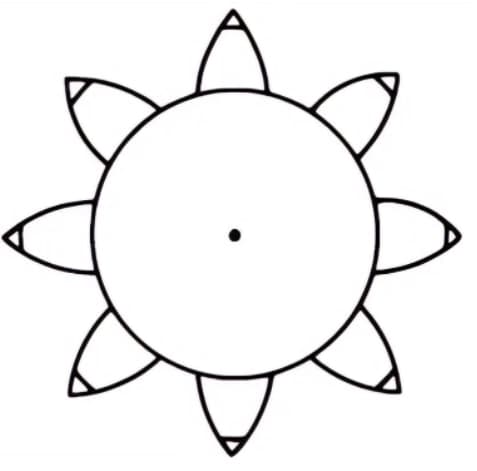
Les avantages des engrenages en développante comprennent leur capacité à transmettre un rapport de vitesse constant, un fonctionnement en douceur grâce à leur schéma de contact qui change progressivement, et une faible sensibilité aux variations de l'entraxe.
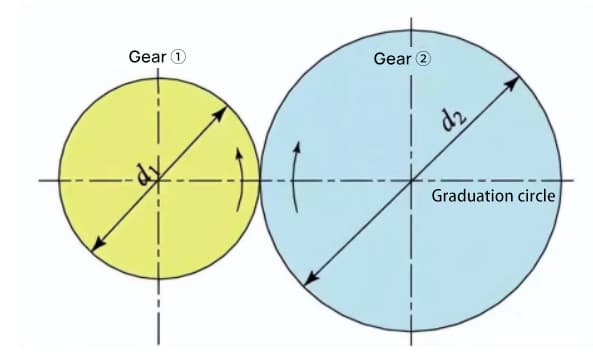
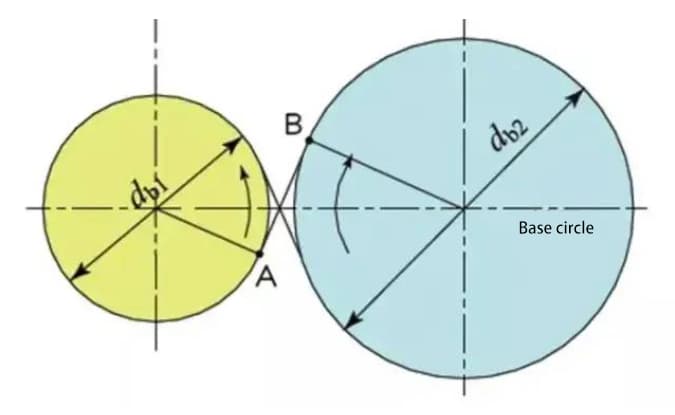
Le cercle de base est le cercle fondamental qui forme le profil de la denture en développante. Le cercle primitif est le cercle de référence qui détermine la taille de l'engrenage. Le cercle de base et le cercle primitif sont des dimensions géométriques importantes des engrenages.
Le profil de la dent en développante est une courbe formée à l'extérieur du cercle de base, et l'angle de pression sur le cercle de base est nul.
Lorsque deux engrenages à développante standard sont engrenés, leurs cercles primitifs sont tangents l'un à l'autre à l'entraxe standard. L'aspect de l'engrènement des deux engrenages ressemble à la transmission de deux roues de frottement de diamètres d1 et d2, respectivement.
Cependant, l'engrènement des engrenages à développante dépend en fait du cercle de base plutôt que du cercle primitif.
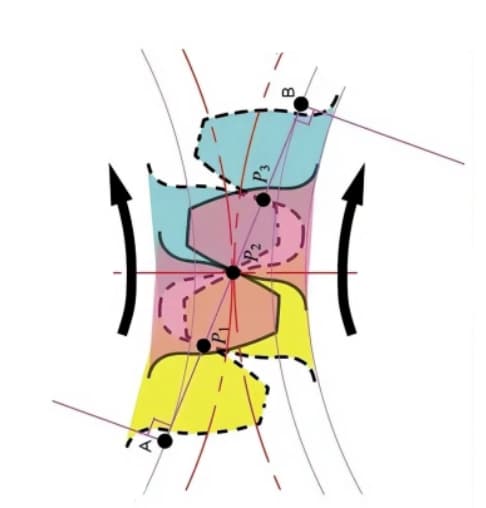
Les points de contact entre les dents d'engrènement de deux engrenages se déplacent le long de la ligne d'action dans l'ordre P1, P2 et P3.
Faites attention à la dent jaune de l'engrenage d'entraînement. Après le début de l'engrènement de cette dent, l'engrenage se trouve dans un état d'engrènement à deux dents (P1, P3) pendant un certain temps. L'engrènement se poursuit et, lorsque le point de contact se déplace vers le point P2 du cercle primitif, il ne reste plus qu'une seule dent en prise.
L'engrènement se poursuit et, lorsque le point de contact se déplace vers le point P3, la dent d'engrenage suivante commence à s'engrener au point P1, formant à nouveau un état d'engrènement à deux dents. De cette manière, l'engrènement à deux dents et l'engrènement à une seule dent des engrenages interagissent et transmettent de manière répétée le mouvement de rotation.
La ligne tangente commune entre les cercles de base, A-B, est appelée ligne d'action. Les points de contact des paires d'engrenages sont tous situés sur cette ligne d'action.
Pour illustrer le propos, on peut dire qu'il s'agit d'une courroie qui passe à la périphérie de deux cercles de base et qui transmet l'énergie par un mouvement de rotation.
Le profil des dents des engrenages que nous utilisons habituellement est généralement une développante standard, mais il existe également des situations dans lesquelles les dents de l'engrenage doivent être déplacées, par exemple pour ajuster l'entraxe ou empêcher le dépassement du plus petit engrenage.
La courbe de la forme de la dent en développante varie en fonction du nombre de dents. Plus il y a de dents, plus la courbe de la forme de la dent tend vers une ligne droite.
Lorsque le nombre de dents augmente, la forme de la racine de la dent devient plus épaisse et la résistance de la roue dentée augmente.
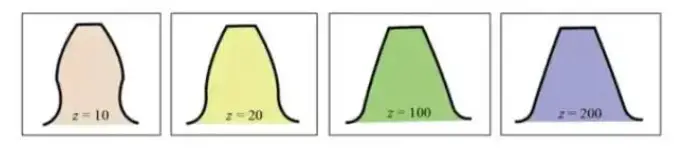
Le graphique ci-dessus montre que pour un engrenage de 10 dents, une partie du profil de la dent en développante à la racine de la dent est enlevée, ce qui entraîne un dépouillement.
Cependant, en adoptant un déplacement positif pour l'engrenage avec z=10, en augmentant le diamètre du cercle d'addendum et en augmentant l'épaisseur des dents de l'engrenage, il est possible d'obtenir la même résistance que celle d'un engrenage avec 200 dents.
Le diagramme suivant montre le schéma d'un engrenage à 10 dents avec déplacement positif. Lors du taillage d'un engrenage, la quantité de mouvement de l'outil le long de la direction radiale est appelée quantité de déplacement radial (appelée quantité de déplacement) xm(mm).
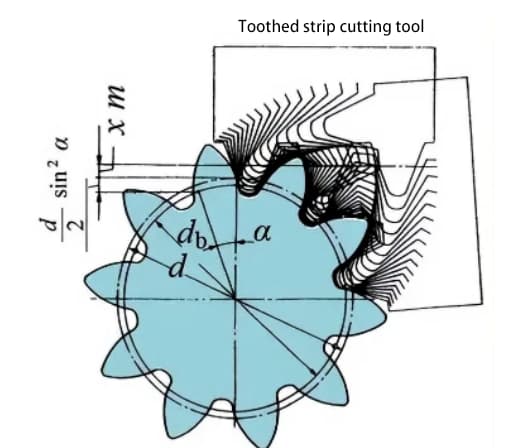
Grâce au déplacement positif du profil de la dent, l'épaisseur de la dent de l'engrenage augmente et le diamètre extérieur (diamètre du cercle d'addition) augmente également.
L'adoption d'un déplacement positif permet d'éviter le sous-coupage des engrenages. Le déplacement des engrenages peut également servir d'autres objectifs, tels que la modification de l'entraxe. Le déplacement positif peut augmenter l'entraxe, tandis que le déplacement négatif peut le réduire.
Qu'il s'agisse d'un engrenage à déplacement positif ou négatif, la quantité de déplacement est limitée.
Le déplacement peut être positif ou négatif. Bien que la hauteur de la denture soit la même, l'épaisseur de la denture est différente. Un engrenage dont l'épaisseur de la dent est plus importante est un engrenage à déplacement positif, tandis qu'un engrenage dont l'épaisseur de la dent est réduite est un engrenage à déplacement négatif.
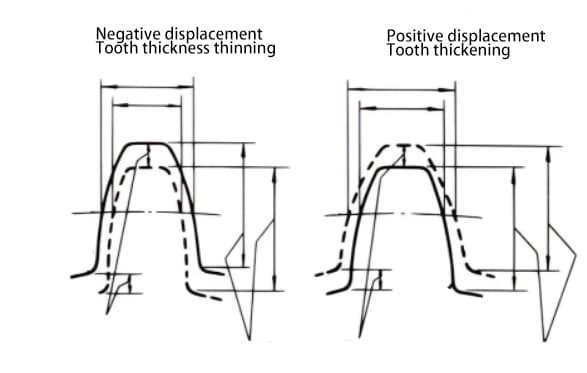
Lorsqu'il n'est pas possible de modifier l'entraxe entre deux engrenages, un déplacement positif peut être appliqué à l'engrenage le plus petit (pour éviter le sous-coupage) et un déplacement négatif à l'engrenage le plus grand, afin d'obtenir le même entraxe. Dans ce cas, la valeur absolue du déplacement est égale.
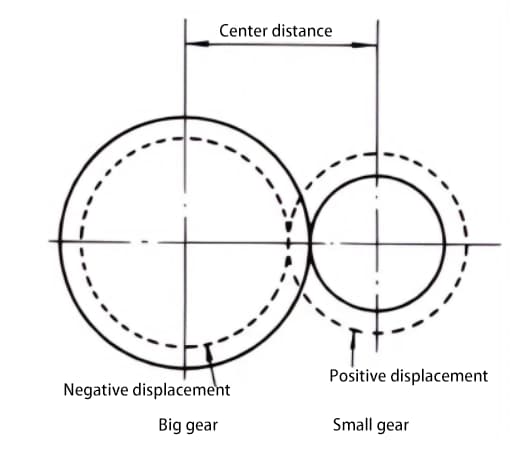
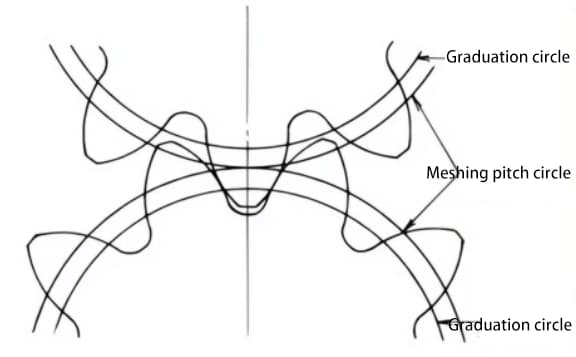
Les engrenages standard s'engrènent lorsque leurs cercles primitifs sont tangents l'un à l'autre. L'engrènement des engrenages déplacés, comme le montre la figure, est tangent l'un à l'autre sur le cercle d'engrènement.
L'angle de pression sur le cercle d'engrènement est appelé angle d'engrènement. L'angle d'engrènement est différent de l'angle de pression sur le cercle primitif (angle de pression sur le cercle primitif) et constitue un facteur important dans la conception des engrenages déplacés.
Le déplacement de l'engrenage permet d'éviter les contre-dépouilles causées par un petit nombre de dents lors de l'usinage. L'entraxe souhaité peut être obtenu par déplacement.
Dans une paire d'engrenages présentant une grande différence dans le nombre de dents, un déplacement positif peut être appliqué à l'engrenage le plus petit, qui s'use facilement, pour augmenter l'épaisseur des dents, tandis qu'un déplacement négatif peut être appliqué à l'engrenage le plus grand pour réduire l'épaisseur des dents, afin de rendre l'espérance de vie des deux engrenages plus comparable.
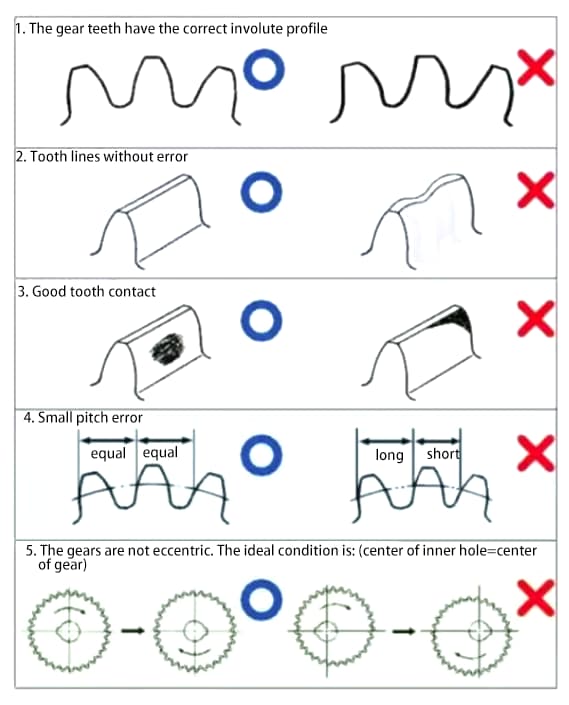
Les engrenages sont des composants mécaniques qui transmettent la puissance et la rotation. Les principales exigences en matière de performance des engrenages sont les suivantes :
Afin de répondre aux exigences susmentionnées, l'amélioration de la précision des engrenages deviendra une tâche nécessaire.
La précision des engrenages peut être divisée en trois catégories :
a) Précision du profil de la dent en développante - précision du profil de la dent
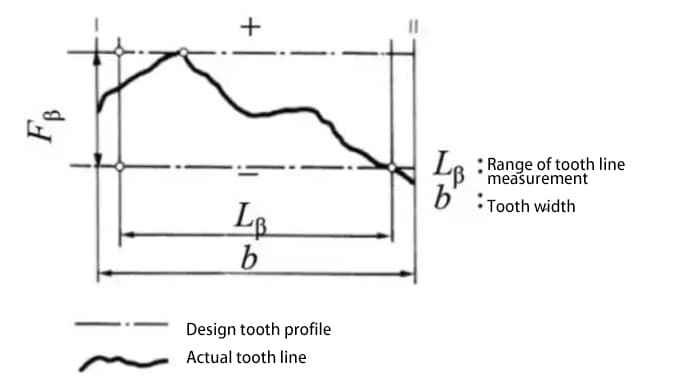
b) Précision de la ligne de flanc de la dent sur la surface de la dent - précision de la ligne de la dent
c) Précision de la position des dents et des fentes.
L'erreur de profil de la dent correspond à l'erreur entre le profil réel de la dent de l'engrenage et le profil théorique de la dent.
De nombreux facteurs influent sur l'erreur de profil de la dent, tels que l'outil et les vibrations de la machine-outil pendant le processus de coupe.
L'erreur de profil de la denture affecte les performances d'engrènement et le bruit de l'engrenage. Il est donc nécessaire de contrôler l'erreur de profil de la dent dans la plage autorisée.
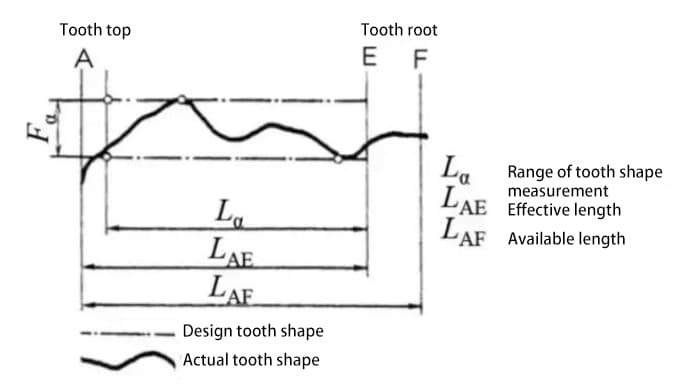
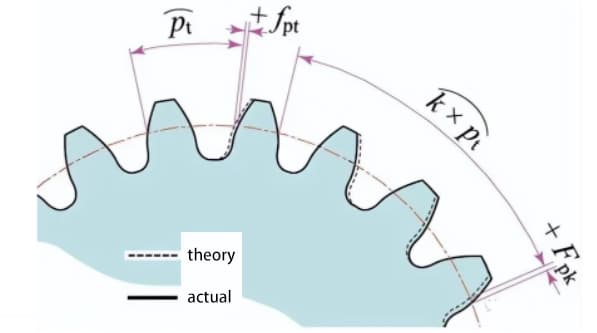
Mesurer la valeur du pas sur la circonférence de mesure centrée sur l'arbre de transmission.
L'écart de pas d'une seule dent (fpt) est la différence entre le pas réel et le pas théorique.
La déviation cumulative totale du pas (Fp) est utilisée pour évaluer la déviation de l'ensemble du pas de l'engrenage. La valeur de l'amplitude totale de la courbe de déviation cumulative du pas représente la déviation totale du pas.
Placez une sonde (sphérique ou cylindrique) successivement dans la gorge de la denture et mesurez la différence entre les distances radiales maximale et minimale entre la sonde et l'axe de l'engrenage. L'excentricité de l'arbre de l'engrenage est l'un des facteurs contribuant au battement radial.
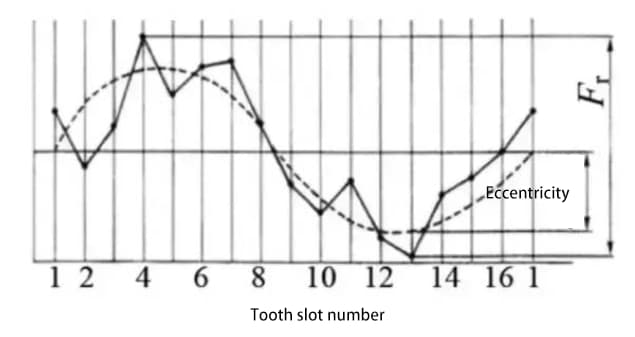
Jusqu'à présent, les méthodes que nous avons décrites pour évaluer la précision des engrenages, telles que la forme des dents, le pas et la précision des flancs de dents, sont toutes des méthodes d'évaluation de la précision d'un engrenage individuel.
En revanche, il existe une autre méthode qui permet d'évaluer la précision de l'engrenage en effectuant un test d'engrènement à deux dents sur l'engrenage en combinaison avec un engrenage de mesure. Les deux surfaces de l'engrenage testé s'engrènent avec l'engrenage de mesure et tournent pendant un cycle complet. La variation de l'entraxe est enregistrée.
La figure ci-dessous montre les résultats du test pour un engrenage de 30 dents. Il y a un total de 30 lignes d'onde pour l'écart composite radial d'une seule dent.
La valeur de l'écart composite radial est approximativement la somme de l'écart de battement radial et de l'écart composite radial d'une seule dent.
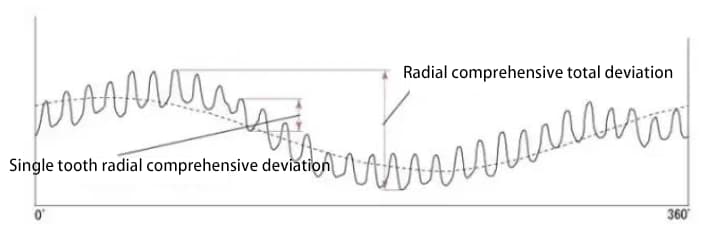
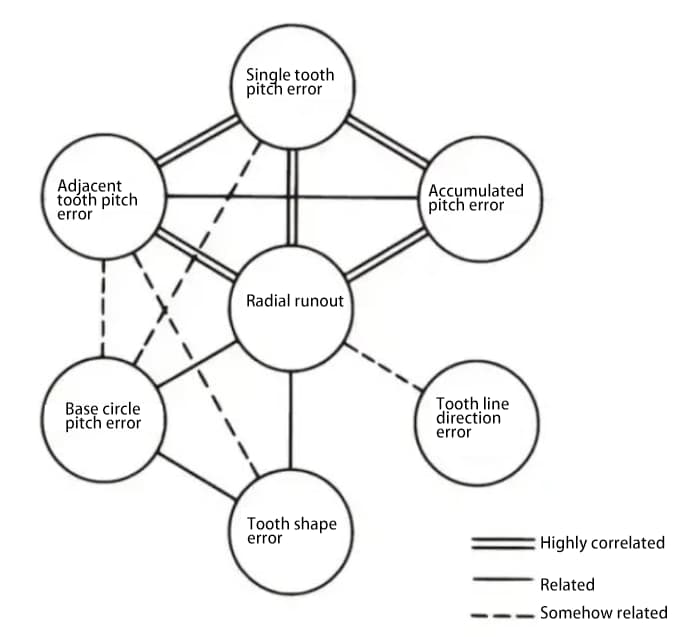
Les différentes parties de la précision de l'engrenage sont liées les unes aux autres. D'une manière générale, le battement radial est fortement corrélé avec d'autres erreurs, et il existe également une forte corrélation entre les différentes erreurs de pas.
Angle de spirale sur une section cylindrique normale :
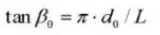
Angle de spirale sur un cylindre de base :
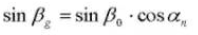
Épaisseur de la dent Angle de centrage :
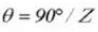
Diamètre de la broche :
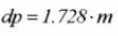
Facteur de correction de l'entraxe :
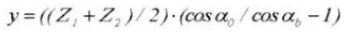
Calcul des engrenages droits standard (pignon ①, roue dentée ②)
1. Nombre de dents sur l'engrenage Standard
2. Engrenage involu standard Engrenage à denture droite
3. Module m
4. Angle de pression
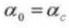
5. Nombre de dents
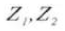
6. Profondeur effective de la dent
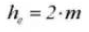
7. Toute la profondeur de la dent
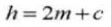
8. Dégagement du pignon
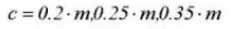
9. Diamètre du cercle primitif de référence
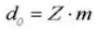
10. Diamètre extérieur
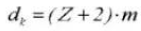
11. Diamètre de la racine
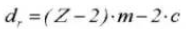
12. Diamètre du cercle de base
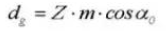
13. Pas circulaire
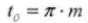
14. Pas diamétral normal
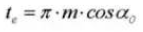
15. Épaisseur de la dent circulaire
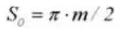
16. Épaisseur de la dent chordale
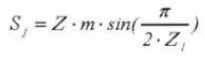
17. Hauteur des dents de la jauge d'huile à engrenages
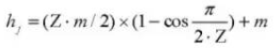
18. Nombre de dents en travers
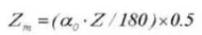
19. Épaisseur de la dent en travers
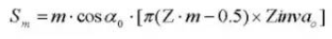
20. Diamètre de la goupille
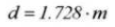
21. Dimension de mesure cylindrique
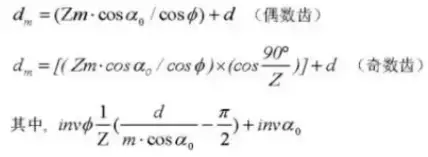
Formule de calcul des engrenages droits déplacés (pignon ①, engrenage ②) :
1. Profil transversal de la denture de l'engrenage
2. Profil de la dent de l'outil Rapport de contact
3. Module m
4. Angle de pression
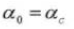
5. Nombre de dents Z
6. Profondeur effective de la dent
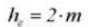
7. Toute la profondeur de la dent
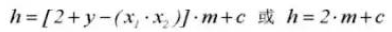
8. Jeu de l'engrenage C
9. Rapport de contact transversal X
10. Distance au centre
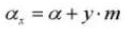
11. Diamètre du cercle primitif de référence
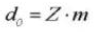
12. Angle de pression de fonctionnement
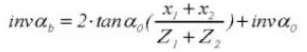
13. Diamètre du cercle primitif
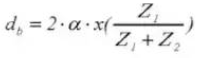
14. Diamètre extérieur
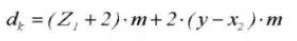
15. Diamètres des addenda
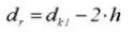
16. Diamètre du pas
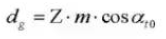
17. Pas circulaire
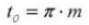
18. Pas diamétral normal
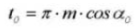
19. Épaisseur de la dent circulaire
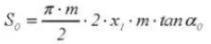
20. Épaisseur de la dent chordale
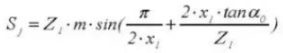
21. Hauteur des dents du pied à coulisse de l'engrenage
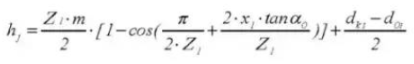
22. Nombre de dents en travers
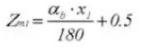
23. Épaisseur de la dent en travers
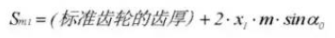
24. Diamètre de l'embout
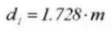
25. Dimension de mesure transversale

Formule de calcul des engrenages hélicoïdaux standard (système normal) (pignon ①, engrenage ②)
1. Profil des dents de l'engrenage Standard
2. Section de référence du système normal de profil dentaire
3. Profil de denture de l'outil Engrenage hélicoïdal
4. Module
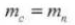
5. Angle de pression
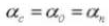
6. Nombre de dents
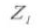
7. Direction de l'hélice
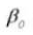
8. Profondeur effective de la dent
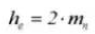
9. Toute la profondeur de la dent
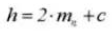
10. Angle de pression frontale
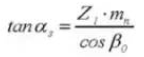
11. Distance au centre
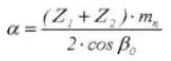
12. Diamètre du cercle primitif de référence
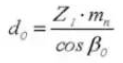
13. Diamètre extérieur
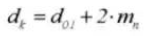
14. Diamètre de la racine
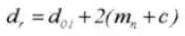
15. Diamètre du pas
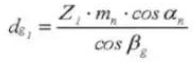
16. Angle de l'hélice sur le cercle de base
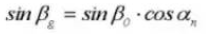
17. Emplacement
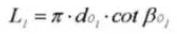
18. Pas circulaire (système normal)
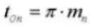
19. Pas diamétral normal (système normal)
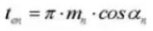
20. Épaisseur de la dent circulaire (système normal)
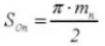
21. Nombre équivalent de dents sur un engrenage droit standard
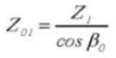
22. Épaisseur de la dent chordale
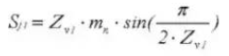
23. Profondeur de dent du pied à coulisse de l'engrenage
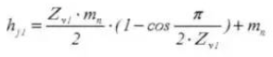
24. Nombre de dents en travers
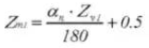
25. Épaisseur de la dent en travers
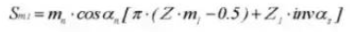
26. Diamètre de l'embout
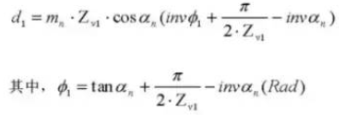
27. Dimension de mesure cylindrique

28. Jeu de l'engrenage f
Formule de calcul des engrenages hélicoïdaux déplacés (système normal) (pignon ①, engrenage ②) :
1. Profil de dent de l'engrenage déplacé
2. Section de référence du système normal de profil dentaire
3. Profil de denture de l'outil Engrenage hélicoïdal
4. Module (système normal)
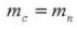
5. Angle de pression (système normal)
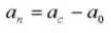
6. Nombre de dents
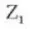
7. Direction de l'hélice
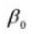
8. Profondeur effective de la dent
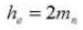
9. Toute la profondeur de la dent
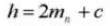
10. Rapport de contact transversal
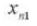
11. Distance au centre
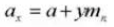
12. Module normal
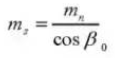
13. Angle de pression avant (système normal)
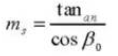
14. Nombre équivalent de dents sur un engrenage droit standard
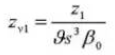
15. Angle de pression normal du système
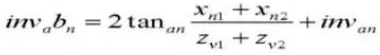
16. Diamètre du cercle primitif de référence
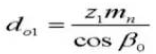
17. Diamètre extérieur
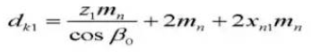
18. Diamètre primitif des dents en contact
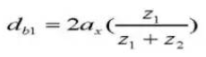
19. Diamètre du pas
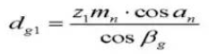
20. Angle de l'hélice sur le cylindre de base
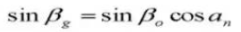
21. Épaisseur de la dent circulaire
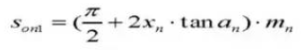
22. Épaisseur de la dent chordale
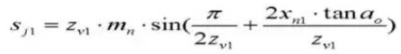
23. Hauteur des dents du pied à coulisse de l'engrenage.
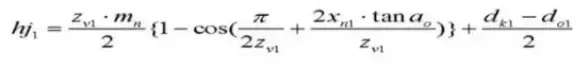
24. Nombre de dents en travers
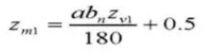
25. Épaisseur de la dent en travers

26. Diamètre de la goupille.
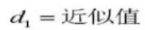
27. Dimension de mesure cylindrique