Vous êtes-vous déjà demandé comment les concepteurs de tôles assurent la précision de leurs dessins ? Dans cet article de blog, nous allons plonger dans le monde fascinant de la conception de tôles et explorer deux concepts essentiels : la surépaisseur de pliage et la déduction de pliage. Nous présenterons également le facteur K et son rôle dans les calculs. Rejoignez-nous pour décortiquer ces sujets et obtenir des informations précieuses de la part d'experts de l'industrie.
Dans le domaine de la conception des tôles, des termes tels que surépaisseur de pliage, déduction de pliage et facteur K sont des concepts cruciaux qui ont un impact significatif sur la précision et l'efficacité des processus de fabrication. Ces paramètres jouent un rôle essentiel dans la détermination des dimensions finales des pièces de tôle pliées et dans la précision de la fabrication. Approfondissons ces concepts et explorons leurs méthodes de calcul.
Les ingénieurs et les fabricants impliqués dans la fabrication de tôles utilisent des algorithmes sophistiqués pour calculer avec précision les dimensions du modèle plat des pièces, garantissant ainsi des géométries finales précises après les opérations de pliage et de formage.
La "méthode du pincement" traditionnelle reste une approche empirique largement utilisée, qui intègre des facteurs tels que les propriétés des matériaux, le rayon de courbure, l'angle de courbure, les configurations d'outillage et les vitesses de formage. Cette méthode, bien qu'efficace, dépend fortement de l'expérience de l'opérateur et peut être sujette à des incohérences.
Avec l'avènement d'outils informatiques avancés, la conception assistée par ordinateur (CAO) et l'analyse par éléments finis (AEF) ont révolutionné la précision et l'efficacité de la conception des tôles. Ces technologies permettent de simuler avec précision le comportement des matériaux au cours des processus de formage, en tenant compte de phénomènes complexes tels que le retour élastique, les contraintes résiduelles et l'écrouissage.
Les systèmes de CAO modernes utilisent des algorithmes avancés de compensation des courbures qui intègrent des modèles théoriques et des données empiriques. Ces algorithmes utilisent généralement l'une des deux approches principales :
Les principales plateformes de CAO, telles que SolidWorks, Autodesk Inventor et Siemens NX, proposent des modules de conception de tôles robustes avec des tables de pliage et des bibliothèques de matériaux personnalisables. Ces systèmes permettent l'intégration de données de pliage spécifiques à l'atelier, ce qui garantit l'alignement entre les conceptions numériques et les processus de fabrication réels.
En outre, des technologies émergentes telles que l'apprentissage automatique et l'intelligence artificielle sont appliquées pour optimiser les calculs de pliage, en exploitant de vastes ensembles de données de production historiques pour affiner les prédictions et s'adapter à des combinaisons uniques de matériaux et d'outillage.
Améliorer la compréhension des lecteurs des concepts de base dans les domaines suivants conception de tôles Les points suivants seront résumés et expliqués :
Pour mieux comprendre indemnité de pliageLa figure 1 illustre le pliage d'une pièce en tôle. La figure 2 montre la pièce dans son état déplié.
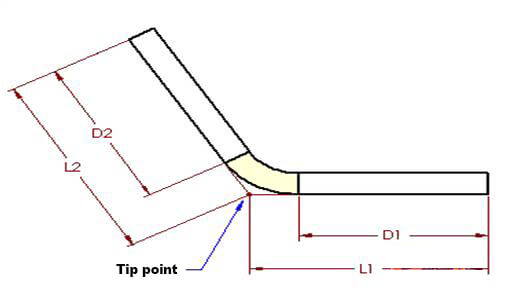
Figure 1
Figure 2
L'algorithme de surépaisseur de pliage décrit la longueur dépliée (LT) d'une pièce de tôle comme la somme des longueurs de chaque segment après aplatissement de la pièce, plus la longueur de la zone de pliage aplatie.
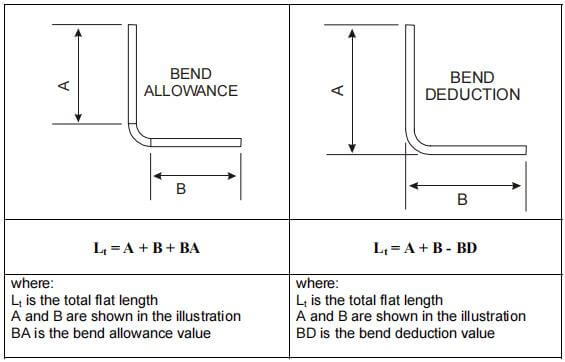
Les indemnité de pliage (BA) représente la longueur de la zone de pliage aplatie. La longueur totale de la pièce peut donc être exprimée par l'équation (1) :
LT = D1 + D2 + BA (1)
La zone de pliage (représentée en jaune clair sur l'illustration) est la zone qui subit théoriquement une déformation pendant le processus de pliage.
Pour déterminer la géométrie de la pièce dépliée, procédez comme suit :
La détermination de la longueur de la zone de flexion aplatie, représentée par BA dans la figure, est un peu plus difficile.
La valeur du BA varie en fonction de facteurs tels que le type et l'épaisseur du matériau, rayon de courbure et l'angle, ainsi que le processus de pliage, le type de machine et la vitesse de la machine.
La valeur de BA peut être obtenue à partir de diverses sources, notamment les fournisseurs de matériaux de tôlerie, les données expérimentales, l'expérience et les manuels d'ingénierie.
Dans SolidWorks, il est possible de saisir directement les valeurs de BA ou d'utiliser le facteur K (qui sera abordé ultérieurement) pour calculer les valeurs.
Les table de pliage est le moyen le plus précis de spécifier différentes tolérances de flexion pour différentes situations avec différentes épaisseurs, différents rayons et différents angles.
La création de la table de pliage initiale peut prendre un certain temps, mais une fois qu'elle est formée, certaines parties peuvent être réutilisées à l'avenir.
Des informations identiques ou différentes peuvent être saisies pour chaque coude de la pièce.
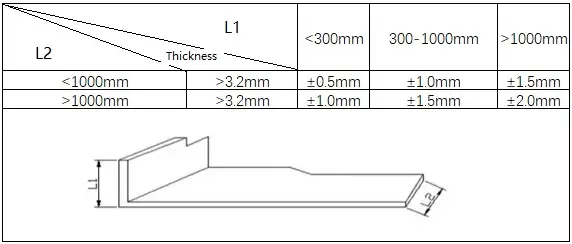
1) Normes pour le cintrage commun
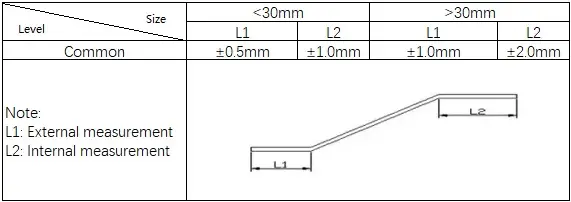
2) Normes pour le pliage en Z
3) Normes pour le cintrage en V
4) Normes pour les Cintrage en U
Lecture connexe : Calculateur de force de pliage en V et en U
La déduction pour cintrage est un terme utilisé pour décrire l'importance du recul dans le processus de cintrage. pliage de tôles. Il s'agit d'un autre algorithme simple pour décrire le processus.
Les figures 1 et 2 s'appliquent également à ce concept. Selon la méthode de la déduction de la flexion, la longueur aplatie (LT) de la pièce est égale à la somme des longueurs des deux sections planes s'étendant jusqu'au "point de pointe" (l'intersection hypothétique des deux sections planes), moins la déduction de la flexion (BD).
Ainsi, la longueur totale de la pièce peut être exprimée comme indiqué dans l'équation (2) :
LT = L1 + L2 - BD (2)
La valeur de la BD peut être déterminée ou obtenue à partir de diverses sources telles que la feuille matériau métallique les fournisseurs, les données expérimentales, l'expérience, les manuels d'ingénierie contenant des équations ou des tableaux, etc.
Figure 3
Il est important que les utilisateurs qui connaissent la méthode de déduction de la flexion comprennent la relation avec la méthode de tolérance de la flexion, qui est couramment adoptée dans SolidWorks.
La relation entre les deux valeurs peut être facilement déduite en utilisant les deux géométries de pliage et de dépliage des pièces.
En comparant les équations (1) et (2), nous avons :
LT = D1 + D2 + BA (1) LT = L1 + L2 - BD (2)
C'est pourquoi,
D1 + D2 + BA = L1 + L2 - BD (3)
Dans la figure 3, l'angle A représente la angle de flexionqui décrit l'angle parcouru par la pièce pendant le pliage, ainsi que l'angle de l'arc formé par la zone de pliage, qui est représentée en deux moitiés.
En utilisant les dimensions et les principes des triangles droits, nous pouvons dériver les équations suivantes :
D1 = L1 - (R + T)TAN(A/2) (4) D2 = L2 - (R + T)TAN(A/2) (5)
En substituant les équations (4) et (5) à l'équation (3), nous pouvons obtenir la relation entre BA et BD :
BA = 2(R + T)TAN(A/2) - BD (6)
Lorsque l'angle de flexion est de 90 degrés, cette équation se simplifie :
BA = 2(R + T) - BD (7)
Ces équations (6) et (7) fournissent une méthode pratique pour passer d'un algorithme à l'autre, en utilisant uniquement l'épaisseur du matériau, l'angle/rayon de flexion, etc. comme paramètres.
Pour les utilisateurs de SolidWorks, ces équations fournissent une méthode directe pour convertir la déduction de pliage en tolérance de pliage.
La valeur de la tolérance de pliage peut être utilisée pour l'ensemble de la pièce ou pour chaque pli individuel, ou elle peut être incluse dans un tableau de données de pliage.
Le facteur K est une valeur autonome qui explique le pliage et le dépliage de la tôle dans divers scénarios géométriques.
Il s'agit également d'une valeur autonome utilisée pour calculer la tolérance de flexion (BA) dans diverses conditions telles que différentes épaisseurs de matériaux, angles de flexion et rayons.
Les figures 4 et 5 sont fournies pour aider à clarifier la définition approfondie du facteur K.
Figure 4
Figure 5
Nous pouvons confirmer qu'il existe un axe neutre dans l'épaisseur de la pièce de tôle. La tôle matériau métallique dans cet axe neutre, la zone de flexion n'est ni étirée ni comprimée, ce qui signifie que c'est la seule zone qui ne se déforme pas pendant la flexion.
Les figures 4 et 5 montrent la limite entre les régions roses et bleues.
Pendant le pliage, la région rose se comprime et la région bleue s'étend. Si la couche de tôle neutre n'est pas déformée, la longueur de son arc dans la zone de pliage reste la même, que la pièce soit pliée ou aplatie.
Par conséquent, la surépaisseur de flexion (BA) doit être égale à la longueur de l'arc de la couche neutre dans la zone de flexion de la pièce de tôle, qui est représentée en vert dans la figure 4.
La position de la couche neutre de la tôle dépend des propriétés d'un matériau spécifique, telles que la ductilité.
On suppose que la distance entre la couche de tôle neutre et la surface est "t", ou la profondeur de la surface de la pièce de tôle dans le matériau dans le sens de l'épaisseur.
Par conséquent, le rayon de l'arc de la couche neutre peut être exprimé comme (R + t). En utilisant cette expression et l'angle de flexion, la longueur de l'arc de la couche neutre (BA) peut être calculée.
BA = Pi(R+T)A/180
Afin de simplifier la définition de la couche neutre de la tôle et de la rendre applicable à tous les matériaux, le concept de facteur K a été introduit.
La définition du facteur K est la suivante : il s'agit du rapport entre l'épaisseur de la couche neutre de la tôle et l'épaisseur totale du matériau de la pièce de tôle. En d'autres termes, le facteur K est défini comme suit :
K = t/T
Par conséquent, la valeur de K sera toujours comprise entre 0 et 1. Si le facteur K est de 0,25, cela signifie que la couche neutre est située à 25% de l'épaisseur totale du matériau de la tôle.
De même, s'il est de 0,5, cela signifie que la couche neutre est située à 50% de toute l'épaisseur, et ainsi de suite.
En combinant les équations mentionnées ci-dessus, on obtient l'équation suivante (8) :
BA = Pi(R+K*T)A/180 (8)
Par conséquent, la valeur de K sera toujours comprise entre 0 et 1.
Si le facteur K est de 0,25, cela signifie que la couche neutre est située à 25% de l'épaisseur de la tôle de la pièce.
De même, si elle est de 0,5, cela signifie que la couche neutre est située à 50% de l'épaisseur totale, et ainsi de suite.
L'origine du facteur K remonte à des sources traditionnelles telles que les fournisseurs de matériaux de tôlerie, les données d'essai, l'expérience, les manuels, etc.
Cependant, dans certains cas, la valeur fournie peut ne pas être exprimée sous la forme d'un facteur K clair, mais il est toujours possible de trouver la relation entre eux.
Par exemple, si un manuel ou une documentation décrit l'axe neutre comme étant "positionné à 0,445x l'épaisseur du matériau par rapport à la surface de la tôle", cela peut être interprété comme un facteur K de 0,445, ce qui signifie k = 0,445.
Lorsque cette valeur de K est substituée à l'équation (8), on obtient la formule suivante.
BA = A (0,01745R + 0,00778T)
Si l'on modifie l'équation (8) par une autre méthode, que l'on calcule la constante de l'équation (8) et que l'on conserve toutes les variables, on obtient ce qui suit :
BA = A (0,01745 R + 0,01745 K*T)
En comparant les deux équations, il est facile de déterminer que 0,01745 * k = 0,00778, et donc que k peut être calculé comme étant 0,445.
On a découvert que le système SolidWorks fournit également un algorithme de surépaisseur de flexion pour des matériaux spécifiques lorsque l'angle de flexion est de 90 degrés. La formule de calcul pour chaque matériau est la suivante :
En fait, en simplifiant l'équation (7) et en fixant l'angle de flexion à 90 degrés, la constante peut être calculée et l'équation peut être transformée comme suit :
BA = (1,57 * K * T) + (1,57 *R)
Par conséquent, en comparant la formule de calcul ci-dessus, la valeur de K pour les matériaux en laiton doux ou en cuivre doux peut être obtenue comme 1,57xk = 0,55, ou K = 0,35.
En utilisant la même méthode, il est facile de calculer les valeurs du facteur K pour les différents types de matériaux énumérés ci-dessus.
Comme nous l'avons vu précédemment, la valeur du facteur K peut être obtenue à partir de plusieurs sources, telles que les fournisseurs de matériaux, les données d'essai, l'expérience et les manuels.
Pour établir un modèle de tôle précis à l'aide de la méthode du facteur K, il est essentiel de trouver la source appropriée de facteur K qui répond à vos exigences d'ingénierie. Cela permettra de s'assurer que les résultats de la pièce physique sont aussi précis que souhaité.
Dans certaines situations, il peut être impossible d'obtenir des résultats précis en utilisant une seule valeur de facteur K, en particulier lorsqu'il est nécessaire de tenir compte d'un large éventail de scénarios de flexion.
Dans ce cas, il est conseillé d'utiliser directement la valeur de la surépaisseur de flexion (BA) pour une seule flexion de la pièce entière, ou d'utiliser un tableau de flexion pour décrire les différentes valeurs de BA, de déduction de flexion (BD) ou de facteur K correspondant à différentes valeurs de A, R et T sur l'ensemble de la gamme.
En outre, des équations peuvent être utilisées pour générer des données telles que l'exemple de tableau de flexion fourni par SolidWorks. Si nécessaire, les cellules du tableau de flexion peuvent également être modifiées sur la base de données expérimentales ou empiriques.
Le répertoire d'installation de SolidWorks comprend des tables de surépaisseur de pliage, des tables de déduction de pliage et des tables de facteur K, qui peuvent être modifiées et personnalisées selon les besoins.
Ce billet présente une vue d'ensemble des méthodes de calcul courantes et de leurs principes sous-jacents utilisés dans la conception et la fabrication de pièces en tôle.
Il couvre le calcul des tolérances de flexion, des déductions de flexion et des facteurs K, et explique les différences entre ces méthodes et leurs interrelations.
Il constitue une référence utile pour les ingénieurs et les professionnels techniques du secteur.
Remarque :
En tant que fondateur de MachineMFG, j'ai consacré plus d'une décennie de ma carrière à l'industrie métallurgique. Ma vaste expérience m'a permis de devenir un expert dans les domaines de la fabrication de tôles, de l'usinage, de l'ingénierie mécanique et des machines-outils pour les métaux. Je suis constamment en train de réfléchir, de lire et d'écrire sur ces sujets, m'efforçant constamment de rester à la pointe de mon domaine. Laissez mes connaissances et mon expertise être un atout pour votre entreprise.
FR 
EN 
AR 
DE 
ES 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO