Fréquence naturelle et fréquence de résonance : La différence expliquée

Dans l'analyse quotidienne, nous confondons souvent la fréquence naturelle et la fréquence de résonance et pensons qu'il s'agit de la même chose.

En fait, ce n'est pas rigoureux.

La fréquence naturelle est la performance des caractéristiques naturelles de la structure, tandis que la fréquence de résonance est la performance de la réponse de la structure sous l'effet des forces extérieures.

Vibration libre d'un système de ressorts à un seul degré de liberté

Un système à un seul degré de liberté est un système dont la position peut être entièrement déterminée par une seule coordonnée généralisée à un moment donné. En termes plus simples, la force agissant sur un corps ne s'exerce que dans une seule direction. Le mouvement de la poupée dans la figure ci-dessous peut être représenté comme un système ressort-masse.

Un modèle simplifié du système de masse-ressort peut être représenté dans la figure suivante.

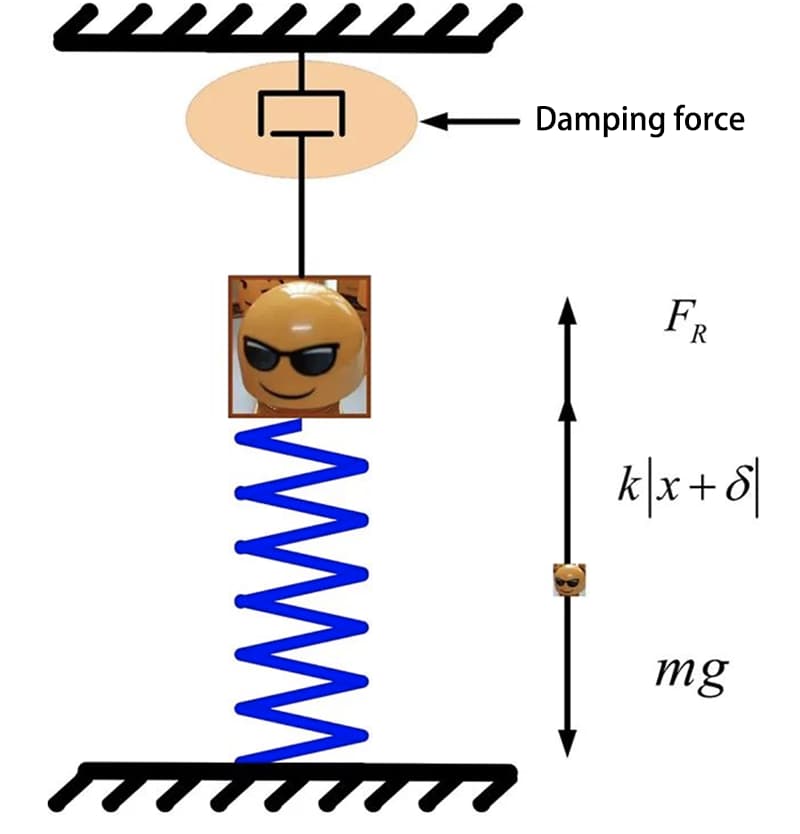
La position d'équilibre statique du bloc de ramassage est considérée comme l'origine des coordonnées, et elle est considérée comme positive lorsqu'elle se déplace verticalement vers le bas le long de la direction de la déformation du ressort. La distance entre le bloc et la position d'équilibre peut être représentée par x, et l'équation différentielle du mouvement du bloc peut être exprimée comme suit :

Où m est la masse du bloc, k est la rigidité du ressort, c est le coefficient de viscosité, 2n=c/m est le coefficient d'atténuation de l'amortissement, et lorsque le coefficient d'amortissement est nul, il correspond à un système vibratoire non amorti.

Fréquence naturelle Pn :

La fréquence naturelle ne dépend que de la masse et de la rigidité et n'est pas affectée par des facteurs tels que l'amortissement. Liaisons structurelles aux limites, propriétés des matériauxLa forme et d'autres facteurs peuvent avoir un impact sur la fréquence naturelle, mais ces influences se reflètent dans la rigidité et la masse et ne sont pas les facteurs déterminants ultimes.

Vibration forcée d'un système de ressorts sous excitation harmonique

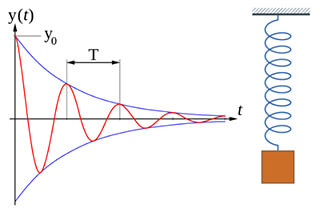
La vibration libre est la vibration du système sans excitation externe, et la trajectoire du mouvement est liée à l'état initial et aux caractéristiques naturelles.

La vibration forcée fait référence à la vibration générée par le système sous l'effet d'une excitation externe.

L'excitation externe est généralement une fonction périodique ou apériodique du temps, l'excitation harmonique simple étant la plus simple.

Soit la force d'excitation harmonique simple :

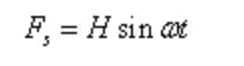
Où H est l'amplitude de la force d'excitation, ω est la fréquence angulaire de la force d'excitation.

Lorsque le bloc s'écarte de la position d'équilibre d'une distance x, l'équation différentielle du mouvement du bloc est la suivante

Où h=H/m, l'équation ci-dessus est l'équation différentielle de la vibration forcée d'un seul degré de liberté avec amortissement visqueux, qui est une équation différentielle ordinaire linéaire non homogène à coefficient constant du deuxième ordre.

L'équation ci-dessus est tout à fait cohérente avec l'expression de la réponse de la tension de la charge capacitive que nous avons apprise dans la théorie des circuits, qui est une équation différentielle ordinaire linéaire non homogène à coefficient constant du deuxième ordre.

L'amortissement du circuit dépend de la résistance, car celle-ci ne fait que consommer de l'énergie et ne la stocke pas.

Sous excitation harmonique simple, la solution totale de l'équation différentielle du mouvement d'un système amorti est définie comme suit :

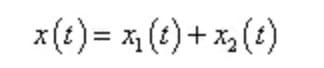
Où x1 (t) est une solution homogène, qui est une vibration libre atténuée ;

En raison de l'existence d'un amortissement, la partie amortie de la vibration disparaît après un certain temps.

Sa solution est la même que celle de la vibration libre, elle ne sera donc pas répétée ici.

Nous nous intéressons ici à la solution spéciale x₂ (t) générée par la vibration forcée, qui peut être exprimée comme suit :

Parmi eux,

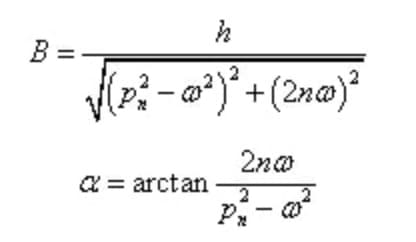
L'amplitude et le retard de phase de la vibration forcée en régime permanent sont indépendants des conditions initiales, mais dépendent uniquement des caractéristiques du système et de l'excitation.

Régler le rapport de fréquence, le rapport d'amortissement et le coefficient d'amplification de l'amplitude comme suit :

La formule ci-dessus peut être réécrite comme suit :

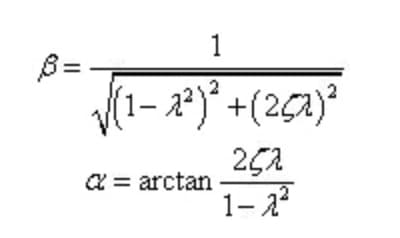
Sur cette base, nous pouvons connaître la réponse du système en cas de vibration forcée.

Pour une meilleure compréhension, la relation entre les différents rapports d'amortissement, les rapports de fréquence et les coefficients d'amplification de l'amplitude peut être illustrée. La fréquence est divisée en trois régions : basse fréquence, moyenne fréquence et haute fréquence. Comme le montre la figure, dans les zones de basse et de haute fréquence, l'amortissement a un impact minimal sur le coefficient d'amplification de l'amplitude. Ainsi, le système amorti peut être simplifié comme un système non amorti pour faciliter les calculs.

Fréquence naturelle et fréquence de résonance

La fréquence propre est une caractéristique inhérente aux propriétés structurelles d'un système, déterminée uniquement par sa masse et sa rigidité, indépendamment de facteurs externes tels que l'amortissement. Dans un système à n degrés de liberté, il existe n fréquences naturelles distinctes, tandis que les systèmes continus possèdent un nombre infini de fréquences naturelles.

La résonance se produit lorsqu'une fréquence d'excitation externe correspond étroitement ou coïncide avec la fréquence naturelle d'un système, ce qui fait vibrer la structure avec une amplitude considérablement accrue. Ce phénomène est représenté par le cercle bleu dans la figure ci-contre. La fréquence de résonance, bien que souvent proche de la fréquence naturelle dans les systèmes légèrement amortis, peut s'en écarter dans les structures fortement amorties, étant généralement inférieure à la fréquence naturelle.

Lors de la conception du système, il est essentiel d'éviter non seulement la fréquence de crête de résonance spécifique, mais aussi la bande de résonance environnante, qui correspond à la région de fréquence intermédiaire de la figure. Cette précaution est nécessaire car la réponse du système reste considérablement amplifiée dans cette bande. Les ingénieurs doivent s'assurer que ni le fonctionnement normal du système ni les excitations externes provenant d'équipements voisins ne se situent dans cette plage critique.

La résonance peut avoir de profondes implications, à la fois bénéfiques et néfastes. Parmi les effets négatifs, on peut citer l'effondrement de poutres de levage, la résonance au sol dans les hélicoptères, l'endommagement des machines et les défaillances structurelles induites par les infrasons. À l'inverse, la résonance est délibérément utilisée dans les instruments de musique pour produire les sons et les harmoniques souhaités.

Pour atténuer les risques liés à la résonance, les concepteurs ont recours à diverses stratégies :

1. Réglage de la fréquence : Ajustement de la fréquence naturelle du système pour éviter les gammes de fréquences opérationnelles.
2. Amélioration de l'amortissement : Incorporation de matériaux ou de mécanismes pour dissiper l'énergie vibratoire.
3. Renforcement structurel : Augmentation de la rigidité pour modifier les fréquences naturelles et réduire les amplitudes.
4. Isolation vibratoire : Mise en œuvre de systèmes visant à minimiser la transmission des excitations externes.
5. Contrôle actif : Utilisation de capteurs et d'actionneurs pour contrer les vibrations résonantes en temps réel.

La compréhension et la gestion de la résonance sont essentielles dans des domaines allant du génie civil et de l'aérospatiale à la fabrication de précision et à la conception d'instruments de musique. Les outils analytiques avancés, tels que l'analyse par éléments finis et l'analyse modale expérimentale, jouent un rôle crucial dans la prédiction et la caractérisation du comportement résonant des systèmes complexes.