Vous êtes-vous déjà demandé pourquoi certains matériaux se plient facilement alors que d'autres restent rigides ? Ce blog plonge dans le monde fascinant du module d'élasticité et de la rigidité, en dévoilant leurs rôles cruciaux dans l'ingénierie. À la fin, vous comprendrez comment ces propriétés influencent la résistance et la flexibilité des matériaux de tous les jours.
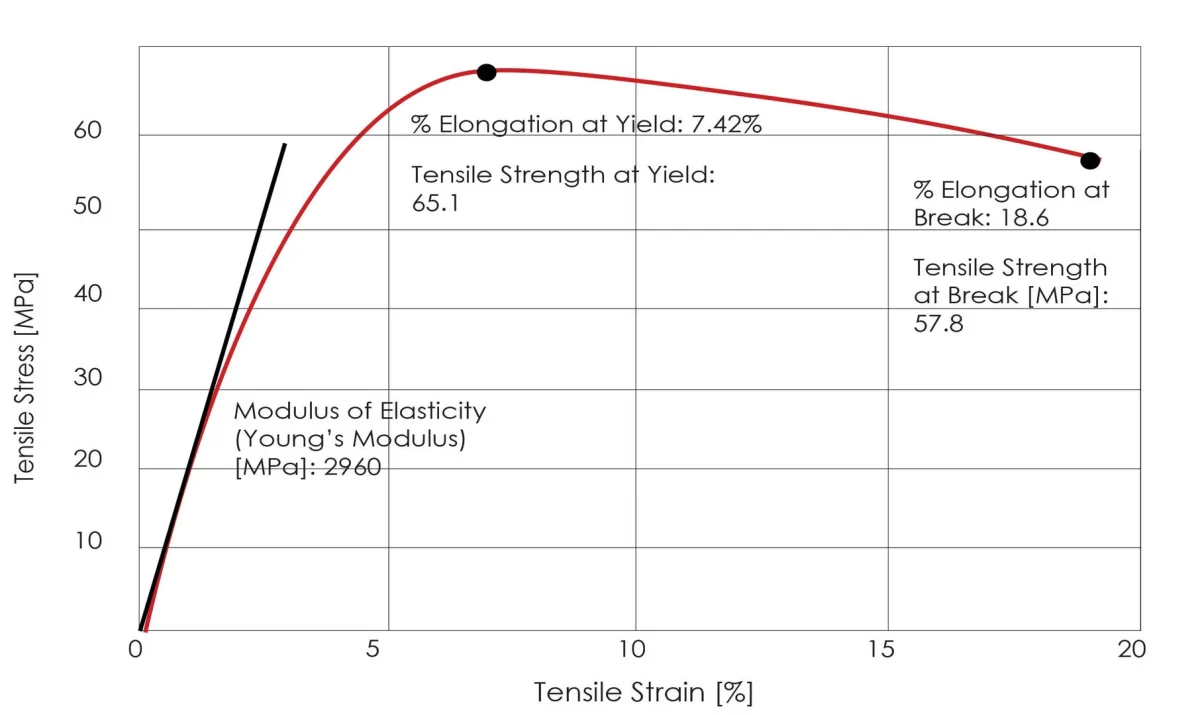
Module d'élasticité : Le rapport entre la contrainte normale et la déformation normale correspondante au stade de la déformation élastique d'un matériau.
Au stade de la déformation élastique, la contrainte et la déformation d'un matériau sont proportionnelles, conformément à la loi de Hooke, et le coefficient de proportionnalité est appelé module d'élasticité.
Le terme "module d'élasticité" est une description générale de l'élasticité d'un matériau. Il englobe plusieurs modules spécifiques, notamment le module de Young, le module de cisaillement et le module de masse, entre autres.
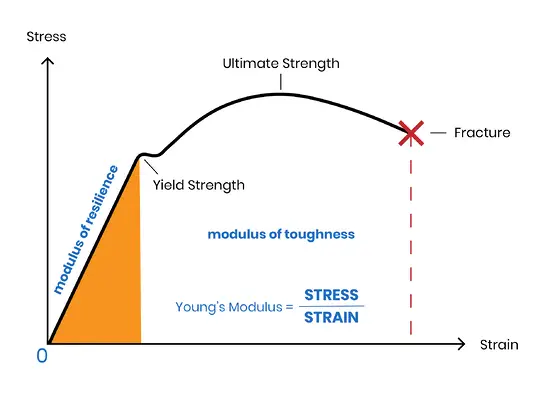
Par conséquent, les termes "module d'élasticité" et "module d'inertie" sont des termes inclusifs.
Lorsqu'une force extérieure (appelée "contrainte") est appliquée à un élastomère, celui-ci change de forme (appelée "déformation"). Le module d'élasticité est défini comme le rapport entre la contrainte et la déformation.
Par exemple :
Déformation linéaire :
Lorsqu'une force de traction F est appliquée à une tige mince, la contrainte linéaire est calculée comme la force de traction divisée par la section transversale S de la tige.
La déformation linéaire est calculée comme l'allongement de la tige (dL) divisé par sa longueur d'origine (L).
La contrainte linéaire divisée par la déformation linéaire est égale au module de Young, E = (F / S) / (dL / L).
Déformation par cisaillement :
Lorsqu'une force latérale (généralement une force de frottement) f est appliquée à un élastomère, celui-ci passe d'une forme carrée à une forme de losange.
Cet angle de déformation est appelé "déformation de cisaillement" et la force correspondante divisée par la zone de contrainte est appelée "contrainte de cisaillement".
La contrainte de cisaillement divisée par la déformation de cisaillement est égale au module de cisaillement, G = (f / S) / a.
Souche de volume :
Lorsqu'une pression globale P est appliquée à l'élastomère, on parle de "contrainte de volume".
La réduction du volume de l'élastomère (-dV) divisée par son volume d'origine (V) est appelée "déformation volumique".
La contrainte volumique divisée par la déformation volumique est égale au module de masse, K = P / (-dV / V).
En général, lorsqu'il n'y a pas de confusion, le module d'élasticité des matériaux métalliques se réfère au module de Young, également connu sous le nom de module d'élasticité positif.
Unité : E (module d'élasticité) est mesuré en GPa.
Le module d'élasticité est un paramètre de performance crucial pour les matériaux d'ingénierie.
D'un point de vue macro, elle mesure la capacité d'un objet à résister à une déformation élastique, tandis que d'un point de vue micro, elle reflète la force de liaison entre les atomes, les ions ou les molécules.
Les facteurs qui affectent la force de liaison peuvent également avoir un impact sur le module d'élasticité d'un matériau, tels que le mode de liaison, la structure cristalline, la composition chimique, la microstructure, la température, etc.
Le module d'Young de matériaux métalliques peut varier de plus de 5% en raison des différentes compositions d'alliage, des états de traitement thermique et des déformations plastiques à froid.
Toutefois, d'une manière générale, le module d'élasticité des matériaux métalliques est un indice de propriétés mécaniques insensible à la structure.
L'alliage, le traitement thermique (structure des fibres) et la déformation plastique à froid ont un effet limité sur le module d'élasticité, et les facteurs externes tels que la température et le taux de charge ont un impact négligeable sur celui-ci.
Par conséquent, dans les applications générales d'ingénierie, le module d'élasticité est considéré comme une constante.
Unité : GPa (gigapascals) pour le module d'élasticité.
Le module d'élasticité est une mesure de la résistance d'un matériau à la déformation élastique.
Plus sa valeur est élevée, plus la contrainte nécessaire pour produire une certaine déformation élastique est importante, ce qui signifie que le matériau est plus rigide et subit moins de déformation élastique sous une contrainte donnée.
Le module d'élasticité, représenté par E, est une mesure de la quantité de contrainte nécessaire pour qu'un matériau subisse une déformation élastique unitaire sous l'effet d'une force extérieure.
Elle représente la capacité du matériau à résister à la déformation élastique et peut être comparée à la rigidité de l'acier. un printemps.
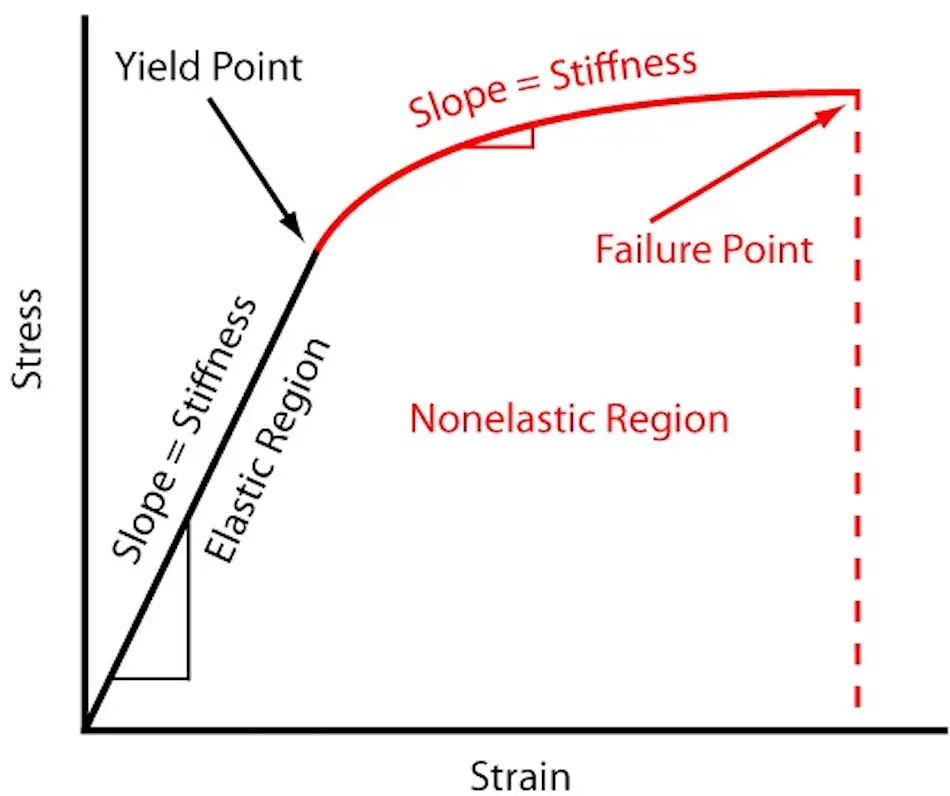
La "rigidité" désigne la capacité d'une structure ou d'un composant à résister à une déformation élastique. Elle est déterminée par la force ou le moment nécessaire pour produire une unité de déformation.
La rigidité en rotation est représentée par "k" et peut être calculée comme "k = M / θ", où "M" est le couple appliqué et "θ" l'angle de rotation.
Les autres raideurs sont les suivantes
La méthode de calcul de la rigidité peut être divisée en deux approches : la théorie des petits déplacements et la théorie des grands déplacements.
La théorie des grands déplacements prend en compte la déformation de la structure après la contrainte et forme l'équation d'équilibre en conséquence, fournissant des résultats précis mais avec un processus de calcul plus complexe.
En revanche, la théorie des petits déplacements suppose que la structure n'est pas déformée de manière significative, de sorte que la force interne peut être obtenue à partir de la charge externe, puis utilisée pour calculer la déformation.
Cette approche est largement utilisée dans la plupart des applications de conception mécanique, car elle est beaucoup plus simple à résoudre.
Par exemple, dans le calcul de la déformation d'une poutre en flexion, la théorie des petits déplacements est souvent utilisée car la déformation réelle est très faible.
Cette théorie consiste à ignorer la dérivée première de la déviation dans la formule de courbure et à utiliser la dérivée seconde de la déviation pour approximer la courbure de l'axe de la poutre, ce qui permet de simplifier le processus de résolution en linéarisant l'équation différentielle.
Lorsque plusieurs charges agissent simultanément, la déformation en flexion causée par chaque charge peut être calculée séparément, puis combinée.
La résistance à la déformation sous une charge statique est appelée rigidité statique, tandis que la résistance à la déformation sous une charge dynamique est appelée rigidité dynamique, c'est-à-dire la quantité de force dynamique requise pour une unité d'amplitude.
Lorsque la force d'interférence varie lentement (c'est-à-dire que la fréquence de la force d'interférence est bien inférieure à la fréquence de la fréquence naturelle de la structure), la rigidité dynamique est essentiellement égale à la rigidité statique.
Toutefois, si la force d'interférence change rapidement (c'est-à-dire si la fréquence de la force d'interférence est beaucoup plus élevée que la fréquence naturelle de la structure), la déformation de la structure sera relativement faible et, par conséquent, la rigidité dynamique sera relativement importante.
Si la fréquence de la force d'interférence est proche de la fréquence naturelle de la structure, une résonance se produit et la rigidité dynamique est à son minimum, ce qui rend la structure la plus facile à déformer, sa déformation dynamique pouvant atteindre plusieurs fois, voire plus de dix fois, la déformation de la charge statique.
Une déformation excessive des composants peut avoir un impact sur leur fonctionnement.
Par exemple, une déformation excessive d'un arbre d'engrenage peut affecter l'engrenage, et une déformation excessive d'une machine-outil peut réduire la précision de l'usinage.
Les facteurs affectant la rigidité comprennent le module d'élasticité des matériaux et la forme de la structure. La modification de la forme de la structure peut avoir un impact significatif sur la rigidité.
Le calcul de la rigidité est le fondement de la théorie des vibrations et de l'analyse de la stabilité structurelle. Lorsque la masse reste constante, une rigidité élevée se traduit par une fréquence naturelle élevée.
La distribution des contraintes dans une structure statiquement indéterminée est liée au rapport de rigidité de chaque partie.
En mécanique des fractures le facteur d'intensité des contraintes d'un élément fissuré peut être déterminé sur la base de sa flexibilité.
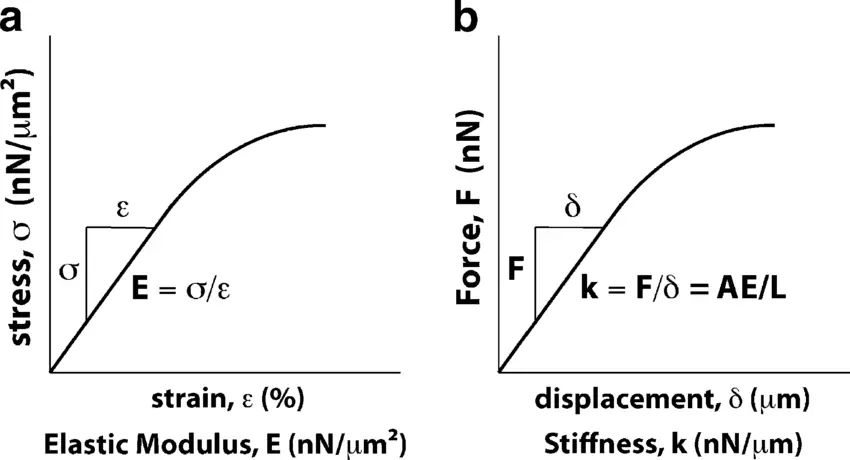
La rigidité et le module d'élasticité sont des concepts fondamentaux de la science des matériaux, chacun décrivant des aspects différents de la résistance d'un matériau à la déformation. Bien qu'ils soient liés, ils jouent des rôles distincts dans l'analyse et l'application des matériaux.
Le module d'élasticité, également connu sous le nom de module de Young, est une mesure spécifique de la capacité inhérente d'un matériau à résister à la déformation sous l'effet d'une contrainte. Il quantifie la relation entre la contrainte (force par unité de surface) et la déformation (déformation proportionnelle) dans la région élastique linéaire de la courbe contrainte-déformation du matériau. Le module d'élasticité est une propriété du matériau et est indépendant de la forme ou de la taille du matériau. Il est exprimé en unités de pression, telles que les Pascals (Pa).
La rigidité, quant à elle, est un terme plus large qui fait référence à la résistance d'une structure à la déformation élastique sous l'effet d'une charge appliquée. Il ne s'agit pas uniquement d'une propriété matérielle, mais elle dépend également de la géométrie et des conditions aux limites de la structure. La rigidité est généralement exprimée comme la force nécessaire pour obtenir un déplacement unitaire (par exemple, Newtons par mètre, N/m).
La rigidité d'un élément structurel peut être dérivée du module d'élasticité du matériau et de la géométrie de l'élément. Par exemple, la rigidité en flexion (EI) d'une poutre est le produit du module d'élasticité (E) et du moment d'inertie (I) de la section transversale de la poutre. De même, la rigidité en torsion (GI) est le produit du module de cisaillement (G) et du moment d'inertie polaire (I).
La rigidité est cruciale dans la conception technique, en particulier pour les composants qui doivent conserver leur forme sous charge, tels que les broches, les rails de guidage et les vis d'entraînement. Elle est également essentielle pour les structures nécessitant un contrôle strict de la déformation, telles que les ailes d'avion et les assemblages de haute précision.
La résistance est la capacité d'un matériau à résister à la déformation permanente et à la rupture sous l'effet de forces extérieures. Elle englobe différents types de résistance, notamment la limite d'élasticité, la résistance à la traction, la résistance à la compression et la résistance à la flexion. Ces propriétés sont essentielles pour déterminer la capacité de charge et la durabilité des pièces mécaniques.
Il est essentiel de comprendre la distinction entre la rigidité et le module d'élasticité pour concevoir et analyser les composants et les structures mécaniques. Alors que le module d'élasticité fournit une mesure de la résistance intrinsèque d'un matériau à la déformation, la rigidité tient compte à la fois des propriétés des matériaux et des facteurs géométriques pour décrire la résistance globale d'une structure à la déformation. Ces deux concepts font partie intégrante de la performance et de la fiabilité des conceptions techniques.
En tant que fondateur de MachineMFG, j'ai consacré plus d'une décennie de ma carrière à l'industrie métallurgique. Ma vaste expérience m'a permis de devenir un expert dans les domaines de la fabrication de tôles, de l'usinage, de l'ingénierie mécanique et des machines-outils pour les métaux. Je suis constamment en train de réfléchir, de lire et d'écrire sur ces sujets, m'efforçant constamment de rester à la pointe de mon domaine. Laissez mes connaissances et mon expertise être un atout pour votre entreprise.
FR 
EN 
AR 
DE 
ES 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO