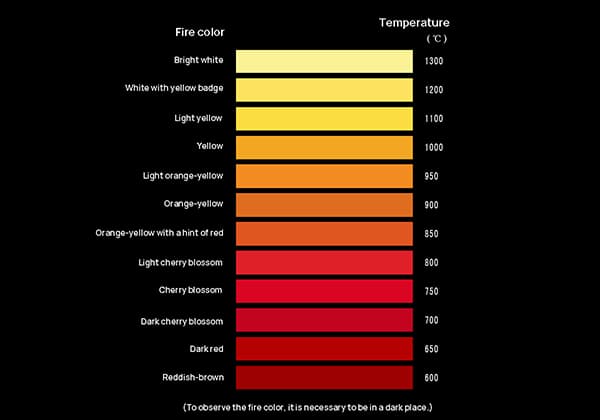
Dans cet article, nous explorons des méthodes d'essai non destructives innovantes qui révèlent la qualité et la résistance réelles des structures en acier. Découvrez comment les scientifiques utilisent des tests de dureté et des formules empiriques pour garantir la sécurité et la fiabilité des projets d'ingénierie. Plongez dans cet article pour découvrir la science fascinante qui se cache derrière ces techniques !
L'évaluation précise de la qualité des structures en acier en service nécessite de déterminer la qualité et la résistance de l'acier. C'est la base d'essais et d'évaluations fiables.
La méthode conventionnelle pour déterminer la résistance de l'acier consiste à prélever des échantillons de la structure pour les soumettre à des essais de traction, mais cette approche peut endommager la structure d'origine et peut ne pas être réalisable pour certaines structures.
Il est donc essentiel d'utiliser des méthodes d'essai non destructives pour calculer la qualité et la résistance de l'acier.
Des chercheurs nationaux et internationaux ont étudié des méthodes d'essai non destructives pour déterminer la résistance de l'acier dans les sites d'ingénierie. Ils se sont principalement concentrés sur la composition chimique et la dureté, et ont développé quelques formules empiriques.
Lecture connexe : Dureté des métaux : Le guide définitif (avec tableau de dureté)
Ces formules empiriques peuvent être classées en deux catégories :
Le premier type consiste à calculer la résistance à la traction sur la base de la composition chimique, comme spécifié dans la formule du document GB/T 50621-2010 Technical Standard for On-site Testing of Steel Structures (Norme technique pour les essais sur site des structures en acier). Cependant, la résistance des matériaux en acier est affectée par la composition chimique et le processus de fabrication (comme le moulage, le forgeage, le laminage et le traitement thermique), de sorte que se baser uniquement sur la composition chimique pour calculer la résistance de l'acier peut entraîner une déviation significative.
Le second type consiste à calculer la résistance à la traction sur la base de la dureté. Des recherches ont montré qu'il existe une corrélation positive entre la dureté et la résistance à la traction de l'acier. La résistance à la traction la résistance des matériaux peut être estimée à partir des résultats des essais de dureté, ce qui est une méthode largement utilisée dans la pratique de l'ingénierie.
À l'heure actuelle, les principales normes nationales pouvant être utilisées à cette fin sont les suivantes : GB/T 33362-2016 Conversion of Hardness Values of Matériaux métalliques et GB/T 1172-1999 Conversion of Hardness and Strength of Ferrous Metals. GB/T 33362-2016 est équivalent à ISO 18265:2013 Conversion des valeurs de dureté des matériaux métalliques. La norme table de conversion de la dureté pour l'acier non allié, l'acier faiblement allié et l'acier moulé dans le tableau A.1 de cette norme a été obtenue par des essais comparatifs avec des duromètres vérifiés et étalonnés dans différents laboratoires par l'Association allemande des ingénieurs métallurgistes. La norme GB/T 1172-1999 a été obtenue grâce à des essais et des recherches approfondis effectués par des institutions telles que l'Académie chinoise de métrologie. Le tableau 2 de la norme fournit principalement la relation de conversion applicable à l'acier à faible teneur en carbone.
Cependant, aucune de ces normes ne fournit de données fiables avec une signification statistique pour l'incertitude des valeurs de conversion, et la plage de déviation des résultats de conversion est inconnue. Les chercheurs ont étudié la corrélation entre la dureté et la résistance de l'acier utilisé dans la construction de structures en acier par le biais d'une analyse de régression et l'ont comparée aux normes nationales, ce qui sert de vérification et de complément aux normes GB/T 33362-2016 et GB/T 1172-1999. Ils ont également discuté de la méthode de détection adaptée aux sites de projets de structures en acier, en intégrant les instruments de détection portables existants.
Les objets de recherche de cette étude sont les plaques d'acier Q235 et Q345 couramment utilisées dans l'ingénierie des structures en acier.
Lecture associée: Acier Q235 vs Q345
Afin de garantir la représentativité des échantillons, 162 plaques d'acier ont été collectées auprès de 86 fabricants de structures métalliques de la province de Jiangsu, dont 82 plaques d'acier Q235 et 80 plaques d'acier Q345. Les spécifications d'épaisseur des plaques d'acier étaient de 6, 8, 10, 12, 14, 18, 20 et 30 mm.
Les plaques d'acier ont été transformées en bandes de 20 mm x 400 mm et les essais de traction ont été réalisés à l'aide d'une machine d'essai de traction servo électro-hydraulique contrôlée par micro-ordinateur, conformément aux exigences de la norme GB/T 228.1-2010.
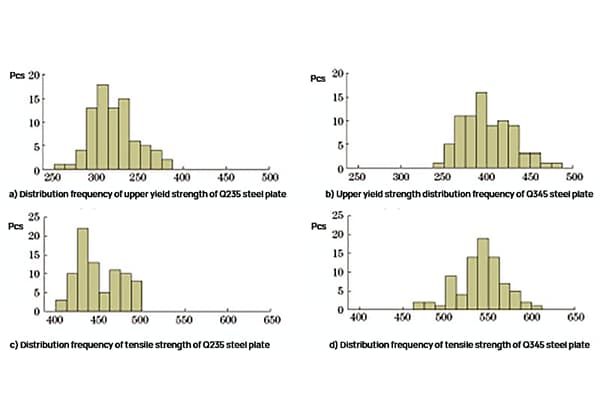
Les résultats des tests de la partie supérieure limite d'élasticité et la résistance à la traction des plaques d'acier Q235 et Q345 ont fait l'objet d'une analyse statistique, et la fréquence de distribution est représentée dans la figure 1.
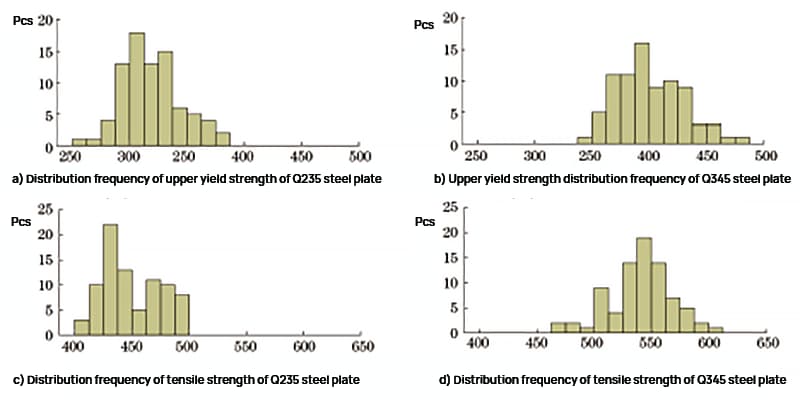
Fig. 1 Fréquence de distribution de la résistance du Q235 Tôle d'acier et plaque d'acier Q345
Comme le montre la figure 1, la limite supérieure d'élasticité de la tôle d'acier Q235 est comprise entre 261 et 382 MPa, et la résistance à la traction est comprise entre 404 et 497 MPa. La limite d'élasticité supérieure de la plaque d'acier Q345 est comprise entre 345 et 477 MPa, et la résistance à la traction entre 473 et 607 MPa.
La distribution des fréquences d'intensité est à peu près normale et les résultats des tests sont conformes aux données des inspections quotidiennes, ce qui indique que les échantillons sont très représentatifs.
Les échantillons ont été prélevés et traités conformément aux exigences de la norme et ont subi des essais de dureté Rockwell, Vickers, Brinell et de traction.
Pour effectuer l'analyse de régression des résultats des tests de dureté et de résistance, la méthode des moindres carrés a été utilisée et le logiciel SPSS a été employé.
2.1.1 Résultats des essais de dureté Rockwell et analyse
La surface de l'échantillon a été poncée à l'aide d'une meuleuse pour s'assurer qu'elle était plane et lisse. L'échelle B a été sélectionnée et l'instrument a été étalonné à l'aide d'un bloc de dureté standard. L'essai de dureté Rockwell a été réalisé conformément aux exigences de la norme GB/T 230.1-2018 Metallic Materials Rockwell Hardness Test Part 1 : Test Method (essai de dureté Rockwell pour les matériaux métalliques, partie 1 : méthode d'essai). Trois points ont été mesurés pour chaque échantillon et la valeur moyenne a été retenue.
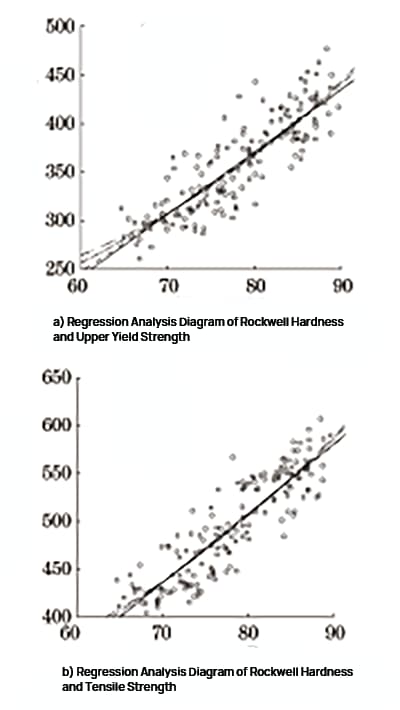
Fig. 2 Analyse de régression de la dureté Rockwell et de la résistance
Le logiciel SPSS a été utilisé pour effectuer des analyses de régression linéaire, de régression quadratique, de régression de puissance et de régression exponentielle sur la dureté Rockwell, la limite d'élasticité supérieure et la résistance à la traction. Le diagramme de l'analyse de régression est illustré à la figure 2, et les résultats de l'analyse de régression sont présentés dans les tableaux 1 et 2.
Tableau 1 Données du modèle de régression de la dureté Rockwell et de la limite supérieure d'élasticité
| Équation | Résumé du modèle | Paramètres du modèle | ||||
| R2 | F | Signification P | constant | b1 | b2 | |
| Exposant linéaire quadratique | 0.736 | 446.897 | 0.000 | -143.077 | 6.426 | 0.081 |
| 0.741 | 227.290 | 0.000 | 341.852 | -6.141 | ||
| 0.740 | 456.461 | 0.000 | 0.828 | 1.392 | ||
| 0.744 | 464.965 | 0.000 | 86.806 | 0.018 | ||
Tableau 2 Données du modèle de régression de la dureté Rockwell et de la résistance à la traction
| Équation | Résumé du modèle | Paramètres du modèle | ||||
| R2 | F | Signification P | constant | b1 | b2 | |
| Exposant linéaire quadratique | 0.780 | 565.900 | 0.000 | -71.394 | 7.241 | 0.074 |
| 0.783 | 286.412 | 0.000 | 372.980 | -4.274 | ||
| 0.778 | 560.887 | 0.000 | 3.477 | 1.137 | ||
| 0.782 | 574.207 | 0.000 | 155.315 | 0.015 | ||
Comme l'indiquent les tableaux 1 et 2, la dureté Rockwell présente une forte corrélation avec la résistance, et la corrélation avec la résistance à la traction est plus forte que celle avec la limite d'élasticité supérieure.
Sur les quatre modèles de régression entre la dureté Rockwell et la résistance, tous ont une signification P inférieure à 0,05 et une qualité d'ajustement R2.
Étant donné que la relation de conversion entre la dureté Rockwell et la résistance à la traction de l'acier à faible teneur en carbone spécifiée dans la norme est similaire au modèle polynomial, il est recommandé d'utiliser le modèle quadratique pour la conversion.
La formule après ajustement est la suivante :
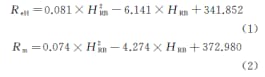
Où : ReH est la limite d'élasticité supérieure ; Rm est la résistance à la traction ; HRB est la dureté Rockwell.
2.1.2 Analyse de l'écart relatif des résultats de conversion
Sur la base du modèle de régression quadratique ajusté, les écarts relatifs entre les valeurs converties de la limite d'élasticité supérieure et de la résistance à la traction et les résultats de l'essai de traction ont été calculés et analysés statistiquement. La taille de l'échantillon était de 162 et les résultats sont présentés dans le tableau 3.
Les écarts relatifs suivent une distribution normale et la distribution des fréquences est présentée dans la figure 3.
Tableau 3 Tableau statistique de l'écart relatif entre la dureté Rockwell et la résistance
| Éléments statistiques | Valeur minimale | Maximum | Écart moyen | Référence standard |
| Écart relatif de la valeur de conversion de la limite d'élasticité supérieure | -16.56 | +16.61 | ±5.46 | 6.84 |
| Écart relatif de la résistance à la traction convertie | -13.31 | +11.16 | ±4.12 | 5.03 |
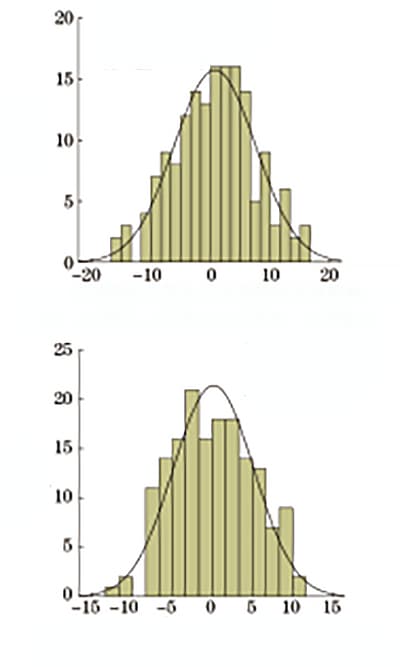
Fig. 3 Écart relatif entre la dureté Rockwell et la résistance
2.1.3 Comparaison avec la valeur de conversion de la norme nationale
La figure 4 présente une comparaison de la valeur de conversion de la résistance à la traction spécifiée dans la norme, de la valeur de conversion de la formule de régression quadratique ajustée et du diagramme de dispersion de la relation correspondante entre la dureté Rockwell et la résistance à la traction, le tout sur le même graphique.
Fig. 4 Tableau de comparaison de la résistance à la traction convertie par la dureté Rockwell
Comme le montre la figure 4, la tendance générale des trois courbes est cohérente. La valeur de conversion de la résistance à la traction indiquée dans la norme GB/T 1172-1999 est similaire à celle de l'auteur, avec un écart moyen de 2,7% et un écart maximal de 5,7% dans la plage de 370 à 630 MPa.
Toutefois, la valeur de conversion de la résistance à la traction indiquée dans la norme GB/T 33362-2016 est inférieure pour l'acier Q235 (dont la résistance à la traction est comprise entre 370 et 500 MPa) et supérieure pour l'acier Q345 (dont la résistance à la traction est comprise entre 470 et 630 MPa).
2.2.1 Processus d'essai de dureté Vickers et analyse des résultats
La surface de l'échantillon a été polie à l'aide d'une meuleuse et l'instrument a été calibré avec un bloc de dureté standard. L'essai de dureté Vickers a été réalisé conformément aux exigences de la norme GB/T 4340.1-2009 Metallic Materials Vickers Hardness Test Part 1 : Test Method (essai de dureté Vickers des matériaux métalliques, partie 1 : méthode d'essai). Trois points ont été mesurés pour chaque échantillon et la valeur moyenne a été retenue.
Le logiciel SPSS a été utilisé pour effectuer des analyses de régression linéaire, de régression quadratique, de régression de puissance et de régression exponentielle sur la dureté Vickers, la limite d'élasticité supérieure et la résistance à la traction. Le diagramme de l'analyse de régression est illustré à la figure 5, et les résultats de l'analyse de régression sont présentés dans les tableaux 4 et 5.
Tableau 4 Données du modèle de régression de la dureté Vickers et de la limite supérieure d'élasticité
| Équation | Résumé du modèle | Paramètres du modèle | ||||
| R2 | F | Signification P | constant | b1 | b2 | |
| Exposant linéaire quadratique | 0.727 | 426.980 | 0.000 | -9.332 | 2.530 | 0.002 |
| 0.728 | 212.272 | 0.000 | 27.358 | 2.020 | ||
| 0.731 | 433.768 | 0.000 | 2.215 | 1.021 | ||
| 0.731 | 435.083 | 0.000 | 126.740 | 0.007 | ||
Fig. 5 Analyse de régression de la dureté Vickers et de la résistance
Tableau 5 Données du modèle de régression de la dureté Vickers et de la résistance à la traction
| Équation | Résumé du modèle | Paramètres du modèle | ||||
| R2 | F | Signification P | Constant | b1 | b2 | |
| Exposant linéaire quadratique | 0.753 | 486.507 | 0.000 | 84.099 | 2.818 | 0.002 |
| 0.753 | 241.944 | 0.000 | 133.182 | 2.136 | ||
| 0.748 | 475.262 | 0.000 | 8.189 | 0.823 | ||
| 0.751 | 483.330 | 0.000 | 213.597 | 0.006 | ||
Comme l'indiquent les tableaux 4 et 5, la dureté Vickers présente une forte corrélation avec la résistance, et la corrélation avec la résistance à la traction est plus forte que celle avec la limite d'élasticité supérieure.
Sur les quatre modèles de régression entre la dureté Vickers et la résistance, tous ont une signification P inférieure à 0,05 et une qualité d'ajustement R2.
Étant donné que la relation de conversion entre la dureté Vickers et la résistance à la traction de l'acier à faible teneur en carbone spécifiée dans la norme est proche d'une relation linéaire, il est recommandé d'utiliser la relation linéaire pour la conversion.
La formule après ajustement est la suivante :
Où : HV est la dureté Vickers.
2.2.2 Analyse de l'écart relatif des résultats de la conversion
Sur la base du modèle de régression linéaire ajusté, les écarts relatifs entre les valeurs converties de la limite d'élasticité supérieure et de la résistance à la traction et les résultats de l'essai de traction ont été calculés et analysés statistiquement. La taille de l'échantillon était de 162 et les résultats sont présentés dans le tableau 6.
Les écarts relatifs suivent une distribution normale et la distribution des fréquences est présentée dans la figure 6.
Tableau 6 Tableau statistique de l'écart relatif entre la dureté Vickers et la résistance
| Éléments statistiques | Valeur minimale | Maximum | Écart moyen | Référence standard |
| Écart relatif de la valeur de conversion de la limite d'élasticité supérieure | -19.30 | +17.55 | ±5.75 | 7.09 |
| Écart relatif de la résistance à la traction convertie | -12.32 | +15.83 | ±4.88 | 5.44 |
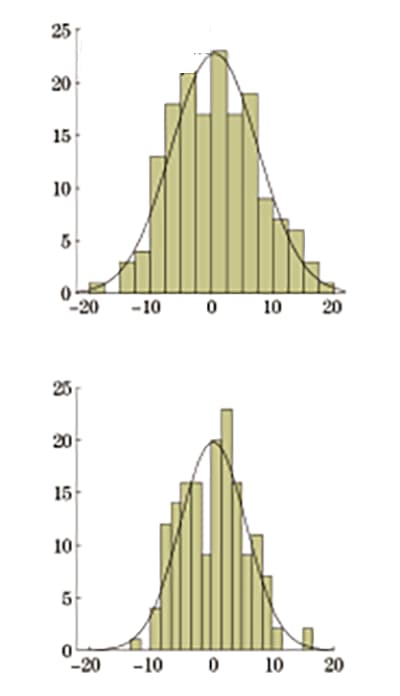
Fig. 6 Écart relatif de la dureté Vickers convertie en résistance
2.2.3 Comparaison avec la valeur de conversion de la norme nationale
La figure 7 compare la valeur de conversion de la résistance à la traction spécifiée dans la norme, la valeur de conversion de la formule de régression linéaire obtenue par l'auteur et le diagramme de dispersion de la relation correspondante entre la dureté Vickers et la résistance à la traction, le tout sur le même graphique.
Fig. 7 Tableau de comparaison de la résistance à la traction convertie en dureté Vickers
Comme le montre la figure 7, la tendance générale des trois courbes est cohérente. La valeur de conversion de la résistance à la traction spécifiée dans la norme GB/T 1172-1999 est très proche de la valeur de conversion obtenue par l'auteur. Dans la plage de 370 à 630 MPa, la différence entre les deux augmente légèrement avec l'augmentation de la valeur de dureté, avec un écart moyen de 1,2% et un écart maximal de 3,3%. Toutefois, la valeur de conversion de la résistance à la traction indiquée dans la norme GB/T 33362-2016 est généralement inférieure.
2.3.1 Dureté Brinell le processus d'essai et l'analyse des résultats
La surface de l'échantillon a été polie à l'aide d'une meuleuse afin d'assurer une bonne stabilité de l'échantillon. rugosité de la surface pas plus de 1,6 μm. L'instrument a été étalonné avec un bloc de dureté standard, et l'essai de dureté Brinell a été réalisé conformément aux exigences de la norme GB/T 231.1-2018 Metallic Materials Brinell Hardness Test Part 1 : Test Method (essai de dureté Brinell des matériaux métalliques, partie 1 : méthode d'essai). A carbure cémenté Un pénétrateur de 10 mm de diamètre a été utilisé et la force d'essai était de 29,42 kN. Trois points ont été mesurés pour chaque échantillon et la valeur moyenne a été retenue.
Le logiciel SPSS a été utilisé pour effectuer des analyses de régression linéaire, de régression quadratique, de régression de puissance et de régression exponentielle sur la dureté Brinell, la limite d'élasticité supérieure et la résistance à la traction. Le diagramme de l'analyse de régression est représenté à la figure 8, et les résultats de l'analyse de régression sont présentés aux tableaux 7 et 8.
Fig. 8 Analyse de régression de la dureté Brinell et de la résistance
Tableau 7 Données du modèle de régression de la dureté Brinell et de la limite supérieure d'élasticité
| Équation | Résumé du modèle | Paramètres du modèle | ||||
| R2 | F | Signification P | constant | b1 | b2 | |
| Exposant linéaire quadratique | 0.756 | 495.403 | 0.000 | -59.965 | 2.846 | -0.001 |
| 0.758 | 246.186 | 0.000 | -86.188 | 3.205 | ||
| 0.757 | 497.365 | 0.000 | 1.048 | 1.168 | ||
| 0.756 | 494.881 | 0.000 | 110.318 | 0.008 | ||
Tableau 8 Données du modèle de régression de la dureté Brinell et de la résistance à la traction
| Équation | Résumé du modèle | Paramètres du modèle | ||||
| R2 | F | Signification P | constant | b1 | b2 | |
| Exposant linéaire quadratique | 0.887 | 1253.313 | 0.000 | -2.613 | 3.377 | -0.001 |
| 0.888 | 631.852 | 0.000 | -225.666 | 6.424 | ||
| 0.889 | 1286.205 | 0.000 | 3.204 | 1.009 | ||
| 0.886 | 1238.834 | 0.000 | 179.073 | 0.007 | ||
Comme l'indiquent les tableaux 7 et 8, la dureté Brinell présente une forte corrélation avec la résistance, et la corrélation avec la résistance à la traction est plus forte que celle avec la limite d'élasticité supérieure.
Sur les quatre modèles de régression entre la dureté Brinell et la résistance, tous ont une signification P inférieure à 0,05 et une qualité d'ajustement R2.
Étant donné que la relation de conversion entre acier au carbone Dureté Brinell et la résistance à la traction spécifiée dans la norme est proche d'une relation linéaire, il est recommandé d'utiliser une relation linéaire pour la conversion.
La formule ajustée est la suivante :
Où : HBW est la dureté Brinell.
2.3.2 Analyse de l'écart relatif des résultats de conversion
Selon le modèle de régression linéaire ajusté, les écarts relatifs entre les valeurs converties de la limite d'élasticité supérieure et de la résistance à la traction et les résultats de l'essai de traction sont calculés respectivement, et les écarts relatifs sont analysés statistiquement.
Les statistiques sont au nombre de 162 et les résultats sont présentés dans le tableau 9.
Les écarts relatifs sont fondamentalement normaux et la distribution des fréquences est illustrée à la figure 9.
Tableau 9 Tableau statistique de l'écart relatif entre la dureté Brinell et la résistance
| Éléments statistiques | Valeur minimale | Maximum | Écart moyen | Référence standard |
| Écart relatif de la valeur de conversion de la limite d'élasticité supérieure | -16.78 | +18.67 | ±5.38 | 6.75 |
| Écart relatif de la résistance à la traction convertie | -9.25 | +8.55 | ±2.89 | 3.59 |
Fig. 9 Écart relatif de la dureté Brinell convertie en résistance
2.3.3 Comparaison avec la valeur de conversion de la norme nationale
Dans la norme GB/T 1172-1999, le rapport entre la force d'essai et le diamètre de la bille du pénétrateur pour l'essai de dureté Brinell est de 10.
Le test de l'auteur est réalisé conformément à la norme GB/T 231.1-2018. Conformément aux dispositions de la norme, le rapport entre la force d'essai et le diamètre de la bille du pénétrateur est de 30.
Par conséquent, elle n'est plus comparée à la norme GB/T 1172-1999 en ce qui concerne la valeur de conversion de la norme nationale.
La valeur de conversion standard de la résistance à la traction indiquée dans la norme GB/T 33362-2016, la valeur de conversion de la formule de régression linéaire ajustée par l'auteur et le diagramme de dispersion de la relation correspondante entre la dureté Brinell et la résistance à la traction sont comparés sur le même graphique, comme le montre la figure 10.
Fig. 10 Tableau de comparaison de la résistance à la traction convertie en dureté Brinell
La figure 10 montre que la valeur de conversion de la résistance à la traction indiquée dans la norme GB/T 33362-2016 coïncide presque avec la courbe de régression de la résistance à la traction ajustée par l'auteur, avec un écart moyen de 0,4% et un écart maximal de 1,2% dans la plage 370-630MPa.
Ces dernières années, le développement rapide de divers appareils d'essai de dureté portables a grandement facilité les essais sur site.
À l'heure actuelle, de nombreux types d'appareils d'essai de dureté Rockwell et Brinell portables peuvent être achetés sur le marché.
L'équipement est portable, simple à utiliser, rapide à mesurer, et la précision de détection répond également aux exigences des normes nationales, ce qui convient à la détection technique sur site.
Il existe également divers équipements de traitement portables pour les échantillons traitement de surfacequi peut répondre aux exigences des tests.
Il est donc possible d'utiliser la dureté Rockwell et la dureté Brinell pour calculer la résistance de l'acier lors de l'inspection sur le terrain des structures en acier.
| Dureté | Résistance à la traction σb/MPa | ||||||||||||||||
| Rockwell | Surface Rockwell | Vickers | Brinell | Acier au carbone | Acier au chrome | Acier au chrome-baryum | Acier au chrome-nickel | Acier au chrome molybdène | Acier au chrome-nickel-molybdène | Acier au chrome-manganèse-silicium | Acier à très haute résistance | Acier inoxydable | Aucun type d'acier spécifique n'est spécifié | ||||
| HRC | HRA | HR15N | HR30N | HR45N | HV | HB30D2 | d10、2d5、4d2.5 /mm | ||||||||||
| 17 | – | 67.3 | 37.9 | 15.6 | 211 | 211 | 4.15 | 73.6 | 706 | 705 | 772 | 726 | – | 757 | – | 703 | 724 |
| 18 | – | 67.8 | 38.9 | 16.8 | 216 | 216 | 4.11 | 753 | 723 | 719 | 779 | 737 | – | 769 | – | 719 | 737 |
| 19 | – | 68.3 | 39.8 | 18 | 221 | 220 | 4.07 | 771 | 739 | 735 | 788 | 749 | – | 782 | – | 737 | 752 |
| 20 | – | 68.8 | 40.7 | 19.2 | 226 | 225 | 4.03 | 790 | 757 | 751 | 797 | 761 | – | 796 | – | 754 | 767 |
| 21 | – | 69.3 | 41.7 | 20.4 | 231 | 227 | 4 | 809 | 775 | 767 | 807 | 775 | – | 810 | – | 773 | 782 |
| 22 | – | 69.8 | 42.6 | 21.5 | 237 | 234 | 3.95 | 829 | 794 | 785 | 819 | 789 | – | 825 | – | 792 | 799 |
| 23 | – | 70.3 | 43.6 | 22.7 | 243 | 240 | 3.91 | 849 | 814 | 803 | 831 | 805 | – | 840 | – | 812 | 816 |
| 24 | – | 70.8 | 44.5 | 23.9 | 249 | 245 | 3.87 | 870 | 834 | 823 | 845 | 821 | – | 856 | – | 832 | 835 |
| 25 | – | 71.4 | 45.5 | 25.1 | 255 | 251 | 3.83 | 892 | 855 | 843 | 860 | 838 | – | 874 | – | 853 | 854 |
| 26 | – | 71.9 | 46.4 | 26.3 | 261 | 257 | 3.78 | 914 | 876 | 864 | 876 | 857 | 876 | 892 | – | 875 | 874 |
| 27 | – | 72.4 | 47.3 | 27.5 | 268 | 263 | 3.74 | 937 | 898 | 886 | 893 | 877 | 897 | 910 | – | 897 | 895 |
| 28 | – | 73 | 48.3 | 28.7 | 274 | 269 | 3.7 | 961 | 920 | 909 | 912 | 897 | 918 | 930 | – | 919 | 917 |
| 29 | – | 73.5 | 49.2 | 29.9 | 281 | 276 | 3.65 | 984 | 943 | 933 | 932 | 919 | 941 | 951 | – | 942 | 940 |
| 30 | – | 74.1 | 50.2 | 31.1 | 289 | 283 | 3.61 | 1009 | 967 | 959 | 953 | 943 | 966 | 973 | – | 966 | 904 |
| 31 | – | 74.7 | 51.1 | 32.3 | 296 | 291 | 3.56 | 1034 | 991 | 985 | 976 | 967 | 991 | 996 | – | 990 | 989 |
| 32 | – | 75.2 | 52 | 33.5 | 304 | 298 | 3.52 | 1060 | 1016 | 1013 | 1001 | 993 | 1018 | 1020 | – | 1015 | 1015 |
| 33 | – | 75.8 | 53 | 34.7 | 312 | 306 | 3.48 | 1086 | 1042 | 1042 | 1027 | 1020 | 1047 | 1046 | – | 1041 | 1042 |
| 34 | – | 76.4 | 53.9 | 25.9 | 320 | 314 | 3.43 | 1113 | 1068 | 1072 | 1054 | 1049 | 1077 | 1073 | – | 1067 | 1070 |
| 35 | – | 77 | 54.8 | 37 | 329 | 323 | 3.39 | 1141 | 1095 | 1104 | 1084 | 1079 | 1108 | 1101 | – | 1095 | 1100 |
| 36 | – | 77.5 | 55.8 | 38.2 | 338 | 332 | 3.34 | 1170 | 1124 | 1136 | 1115 | 1111 | 1141 | 1130 | – | 1126 | 1131 |
| 37 | – | 78.1 | 56.7 | 39.4 | 347 | 341 | 3.3 | 1200 | 1153 | 1171 | 1148 | 1144 | 1176 | 1161 | – | 1153 | 1163 |
| 38 | – | 78.7 | 57.6 | 40.6 | 357 | 350 | 3.26 | 1231 | 1184 | 1206 | 1132 | 1179 | 1212 | 1194 | – | 1184 | 1197 |
| 39 | 70 | 79.3 | 58.6 | 41.8 | 367 | 360 | 3.21 | 1263 | 1216 | 1243 | 1219 | 1216 | 1250 | 1228 | 1218 | 1216 | 1232 |
| 40 | 70.5 | 79.9 | 59.5 | 43 | 377 | 370 | 3.17 | 1296 | 1249 | 1282 | 1257 | 1254 | 1290 | 1264 | 1267 | 1250 | 1268 |
| 41 | 71.1 | 80.5 | 60.4 | 44.2 | 388 | 380 | 3.13 | 1331 | 1284 | 1322 | 1298 | 1294 | 1331 | 1302 | 1315 | 1286 | 1307 |
| 42 | 71.6 | 81.1 | 61.3 | 45.4 | 399 | 391 | 3.09 | 1367 | 1322 | 1364 | 1340 | 1336 | 1375 | 1342 | 1362 | 1325 | 1347 |
| 43 | 72.1 | 81.7 | 62.3 | 46.5 | 411 | 401 | 3.05 | 1405 | 1361 | 1407 | 1385 | 1379 | 1420 | 1384 | 1409 | 1366 | 1389 |
| 44 | 72.6 | 82.3 | 63.2 | 47.7 | 423 | 413 | 3.01 | 1445 | 1403 | 1452 | 1431 | 1425 | 1467 | 1427 | 1455 | 1410 | 1434 |
| 45 | 73.2 | 82.9 | 64.1 | 48.9 | 436 | 424 | 2.97 | 1488 | 1448 | 1498 | 1480 | 1472 | 1516 | 1474 | 1502 | 1457 | 1480 |
| 46 | 73.7 | 83.5 | 65 | 50.1 | 449 | 436 | 2.93 | 1533 | 1497 | 1547 | 1531 | 1522 | 1567 | 1522 | 1550 | 1508 | 1529 |
| 47 | 74.2 | 84 | 65.9 | 51.2 | 462 | 449 | 2.89 | 1581 | 1549 | 1597 | 1584 | 1573 | 1620 | 1573 | 1600 | 1563 | 1581 |
| 48 | 74.7 | 84.6 | 66.8 | 52.4 | 478 | 401 | 2.85 | 1631 | 1605 | 1649 | 1640 | 1626 | 1676 | 1627 | 1652 | 1623 | 1635 |
| 49 | 75.3 | 85.2 | 67.7 | 53.6 | 493 | 474 | 2.81 | 1686 | 1666 | 1702 | 1698 | 1682 | 1733 | 1683 | 1707 | 1688 | 1692 |
| 50 | 75.8 | 85.7 | 68.6 | 54.7 | 509 | 488 | 2.77 | 1744 | 1731 | 1758 | 1758 | 1739 | 1793 | 1742 | 1765 | 1759 | 1753 |
| 51 | 76.3 | 86.3 | 69.5 | 55.9 | 525 | 501 | 2.73 | – | 1803 | 1816 | 1821 | 1799 | 1854 | 1804 | 1827 | – | 1817 |
| 52 | 76.9 | 86.8 | 70.4 | 57.1 | 543 | – | – | – | 1881 | 1875 | 1887 | 1861 | 1918 | 1870 | 1894 | – | 1885 |
| 53 | 77.4 | 87.4 | 71.3 | 58.2 | 561 | – | – | – | – | 1937 | 1955 | 1925 | 1985 | 1938 | 1967 | – | 1957 |
| 54 | 77.9 | 87.9 | 72.2 | 59.4 | 579 | – | – | – | – | 2000 | 2025 | – | – | 2010 | 2045 | – | 2034 |
| 55 | 78.5 | 88.4 | 73.1 | 60.5 | 599 | – | – | – | – | 2066 | 2098 | – | – | 2086 | 2131 | – | 2115 |
| 56 | 79 | 88.9 | 73.9 | 61.7 | 620 | – | – | – | – | – | – | – | – | – | 2224 | – | 2201 |
| 57 | 79.5 | 89.4 | 74.8 | 62.8 | 642 | – | – | – | – | – | – | – | – | – | 2324 | – | 2293 |
| 58 | 80.1 | 89.8 | 75.6 | 63.9 | 664 | – | – | – | – | – | – | – | – | – | 2437 | – | 2391 |
| 59 | 80.6 | 90.2 | 76.5 | 65.1 | 688 | – | – | – | – | – | – | – | – | – | 2558 | – | 2496 |
| 60 | 81.2 | 90.6 | 77.3 | 66.2 | 713 | – | – | – | – | – | – | – | – | – | 2691 | – | 2607 |
| 61 | 81.7 | 91 | 78.1 | 67.3 | 739 | – | – | – | – | – | – | – | – | – | – | – | – |
| 62 | 82.2 | 91.4 | 79 | 68.4 | 766 | – | – | – | – | – | – | – | – | – | – | – | – |
| 63 | 82.8 | 91.7 | 79.8 | 69.5 | 795 | – | – | – | – | – | – | – | – | – | – | – | – |
| 64 | 83.3 | 91.9 | 80.6 | 70.6 | 825 | – | – | – | – | – | – | – | – | – | – | – | – |
| 65 | 83.9 | 92.2 | 81.3 | 71.7 | 856 | – | – | – | – | – | – | – | – | – | – | – | – |
| 66 | 84.4 | – | – | – | 889 | – | – | – | – | – | – | – | – | – | – | – | – |
| 67 | 85 | – | – | – | 923 | – | – | – | – | – | – | – | – | – | – | – | – |
| 68 | 85.5 | – | – | – | 959 | – | – | – | – | – | – | – | – | – | – | – | – |
| 69 | 86.1 | – | – | – | 997 | – | – | – | – | – | – | – | – | – | – | – | – |
| 70 | 86.6 | – | – | – | 1037 | – | – | – | – | – | – | – | – | – | – | – | – |
(1) La dureté Rockwell, la dureté Vickers et la dureté Brinell présentent une bonne corrélation avec la résistance. Sur la base des essais de matériaux, la formule de conversion de la dureté Rockwell, de la dureté Vickers et de la dureté Brinell avec la résistance est obtenue, et l'écart relatif de conversion se situe dans la fourchette admissible du projet.
L'écart relatif entre la dureté Brinell et la résistance à la traction est manifestement plus faible que celui de la dureté Rockwell et de la dureté Vickers.
(2) La résistance à la traction convertie de la dureté Rockwell indiquée dans le document GB/T 33362-2016 est faible pour l'acier Q235 et élevée pour l'acier Q345.
La résistance à la traction convertie en dureté Vickers est légèrement inférieure.
La résistance à la traction convertie en dureté Brinell est cohérente avec les résultats des essais.
Les valeurs de résistance à la traction converties par la dureté Rockwell et la dureté Vickers indiquées dans le document GB/T 1172-1999 sont proches des résultats des essais.
(3) Combinée aux instruments d'essai de dureté portables existants et à l'équipement de traitement des échantillons, l'utilisation de la dureté Rockwell et de la dureté Brinell pour calculer la résistance de l'acier est opérationnelle dans les projets pratiques et peut être appliquée à la pratique de l'ingénierie.
En tant que fondateur de MachineMFG, j'ai consacré plus d'une décennie de ma carrière à l'industrie métallurgique. Ma vaste expérience m'a permis de devenir un expert dans les domaines de la fabrication de tôles, de l'usinage, de l'ingénierie mécanique et des machines-outils pour les métaux. Je suis constamment en train de réfléchir, de lire et d'écrire sur ces sujets, m'efforçant constamment de rester à la pointe de mon domaine. Laissez mes connaissances et mon expertise être un atout pour votre entreprise.
FR 
EN 
AR 
DE 
ES 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO