Vous êtes-vous déjà demandé comment fonctionnent les minuscules rivets qui maintiennent ensemble des structures massives ? Dans cet article, nous dévoilerons le monde fascinant des assemblages par rivets, en explorant leurs types, les calculs de résistance et les applications réelles. À la fin, vous comprendrez le rôle crucial que jouent ces petits composants dans les merveilles de l'ingénierie. Restez à l'écoute pour découvrir comment les rivets maintiennent notre monde solidement attaché !
Les rivets sont une méthode fondamentale pour assembler deux ou plusieurs pièces de matériau, en particulier de métal, et sont largement utilisés dans diverses applications d'ingénierie et de construction. Les rivets, qui sont des attaches mécaniques permanentes, sont constitués d'une tige cylindrique lisse munie d'une tête à une extrémité. Le processus d'installation consiste à insérer le rivet dans un trou pré-percé, puis à déformer la queue pour créer une deuxième tête, ce qui permet de fixer les matériaux ensemble.
Historiquement, les assemblages rivetés ont joué un rôle essentiel dans la construction de structures importantes. La Tour Eiffel à Paris et le Golden Gate Bridge à San Francisco en sont des exemples notables. Ces structures illustrent la durabilité et la solidité des assemblages rivetés, qui ont résisté à l'épreuve du temps et continuent de fonctionner de manière fiable.
La disposition des rivets en chaîne, en zig-zag ou en quinconce influe sur les performances du joint.
Les rivets peuvent être fabriqués à partir de différents matériaux, notamment l'aluminium, l'acier, le laiton et le cuivre. Le choix du matériau dépend d'exigences spécifiques telles que la solidité, la résistance à la corrosion et la ductilité.
Les assemblages rivetés sont privilégiés dans les scénarios où l'assemblage doit résister à des charges dynamiques et où il est nécessaire d'assembler des matériaux dissemblables. Ils sont également choisis en raison de leur importance historique et de leur fiabilité éprouvée dans les structures critiques.
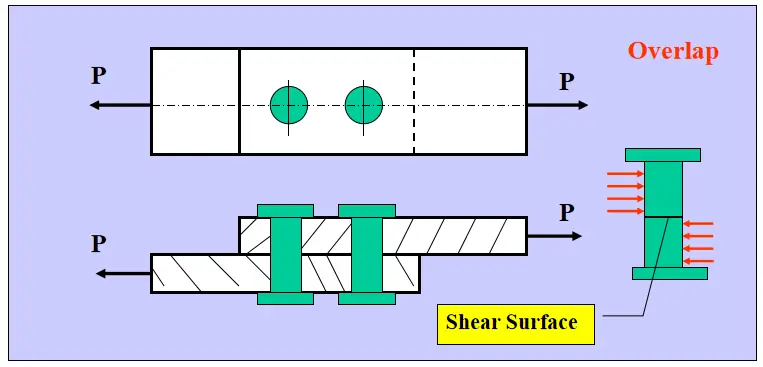
Joint bout à bout à couvercle unique
Joint bout à bout à double couverture
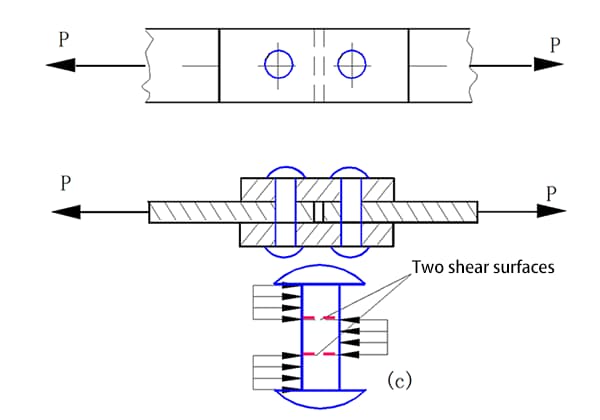
Portée latérale du groupe de rivets
Dans le cas d'un assemblage riveté (comme le montre la figure ci-dessus), pour simplifier les calculs, on suppose que :
La formule pour calculer la force agissant sur chaque rivet est la suivante :
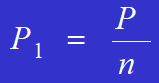
Exemple :
Un joint utilisant quatre rivets est utilisé pour relier deux plaques d'acier. Le matériau des plaques d'acier et des rivets est le même. Le diamètre des rivets est de d=16mm, la taille de la plaque d'acier est de d=16mm. tôle d'acier est b=100mm, t=10mm, P=90KN, la contrainte admissible des rivets est [τ]=120MPa, la limite d'élasticité admissible est [σjy]=120MPa, et la contrainte de traction admissible de la plaque d'acier est de [σ]=160MPa. Calculez et vérifiez la résistance de l'assemblage riveté.
(1) Résistance au cisaillement des rivets :
La force agissant sur chaque rivet est P/4.
La force de cisaillement agissant sur chaque rivet est donnée par :
(2) Résistance à l'écrasement des rivets :
La force agissant sur chaque rivet en raison de l'écrasement est :
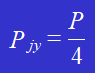
La zone du rivet qui est écrasée est :
(3) Résistance à la traction de la tôle d'acier
Question de réflexion :
Surface de cisaillement de la cheville A.
Surface d'extrusion de la cheville Ajy.
Question complémentaire :
Percez un trou de la forme indiquée dans la figure sur un 5mm d'épaisseur plaque d'acier. Si la limite de résistance au cisaillement du matériau de la plaque d'acier est 𝜏𝑏 = 300MPa, calculez la force de poinçonnage F requise pour le poinçonneuse.
Solution : L'aire de la surface de cisaillement est
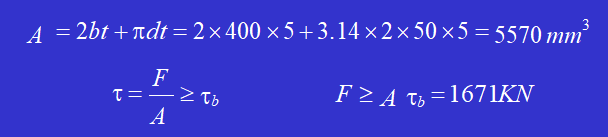
Question complémentaire :
La force de perforation maximale d'un poinçonneuse est P = 400KN, la contrainte de compression admissible [𝜎] du matériau du poinçon est de 440MPa, et la limite de résistance au cisaillement de la plaque d'acier est 𝜏𝑏 = 360MPa. Déterminez le diamètre minimal d que le poinçon peut perforer et l'épaisseur maximale 𝜹 de la plaque d'acier qui peut être perforée.
Solution : Le poinçon subit une déformation de compression axiale.
En fonction de la condition de rupture en cisaillement de la plaque d'acier :
Exemple :
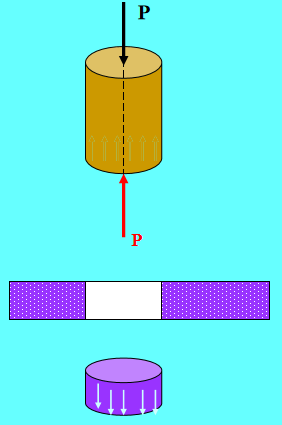
En utilisant deux rails en acier à riveter dans une poutre composite, la situation de connexion est illustrée dans les figures a et b.
La section transversale de chaque rail en acier A est de 8000 mm, et le moment d'inertie de la section transversale de chaque rail en acier par rapport à son propre centroïde est I = 1600 × 10 mm. L'espacement des rivets s est de 150 mm, le diamètre est d = 20 mm et la contrainte de cisaillement admissible [τ] est de 95MPa. Si la force de cisaillement interne Q de la poutre est de 50kN, vérifiez la résistance au cisaillement des rivets. Le frottement entre les rails supérieurs et inférieurs en acier n'est pas pris en compte.
Solution : Lorsque les deux rails en acier supérieur et inférieur se plient dans leur ensemble, la section transversale du rail en acier supérieur est soumise à un effort de compression et la section transversale du rail en acier inférieur est soumise à un effort de traction.
En raison des différents moments de flexion sur les sections transversales adjacentes, la contrainte normale aux points correspondants est différente, et il y a donc une tendance au déplacement longitudinal le long de la surface de contact entre les rails d'acier supérieurs et inférieurs, ce qui entraîne des forces de cisaillement sur les rivets.
L'effort de cisaillement supporté par chaque rangée de rivets est égal à la différence d'effort de compression (traction) sur deux sections transversales d'un rail en acier à une distance longitudinale de S.
En supposant que les rails en acier transmettent des contraintes de cisaillement partout sur la surface de contact, la largeur de la surface de contact est b.
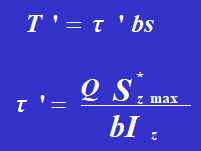
Szmax représente le moment statique de la section transversale d'un rail en acier par rapport à l'axe neutre.
Iz est le moment d'inertie de l'ensemble de la section transversale par rapport à l'axe neutre.
La contrainte de cisaillement du rivet est :
La contrainte de cisaillement du rivet satisfait aux critères de résistance.
Assemblage de rivets soumis à des charges de torsion (voir figure).
Le point 0 est le centroïde de la section transversale de l'assemblage de rivets.
En supposant que toute ligne droite sur la plaque d'acier (telle que OA ou OB) reste droite après la rotation, la déformation moyenne en cisaillement de chaque rivet est proportionnelle à la distance entre le centre de la section transversale du rivet et le point O.
Si le diamètre de chaque rivet est identique, la force exercée sur chaque rivet est proportionnelle à la distance entre le centre de la section du rivet et le centre de la section O de l'assemblage du rivet, la direction étant perpendiculaire à la ligne reliant le point et le centre O.
Pi représente la force agissant sur chaque rivet, et ai représente la distance entre le centre de la section transversale du rivet donné et le centroïde de la section transversale de l'assemblage de rivets, noté O.
L'assemblage de rivets soumis à des charges latérales excentriques (voir figure a).
En simplifiant la charge excentrique P agissant sur l'assemblage de rivets au point centroïde O, on obtient une force P passant par le point O et un moment m = Pe qui tourne autour du point O.
Si le diamètre de chaque rivet d'un même assemblage de rivets est identique, on peut calculer la force P1′ causée par la force latérale P et la force P1" causée par le moment m. La force agissant sur chaque rivet est la somme vectorielle de P1′ et P1". Après avoir déterminé la force P1 sur chaque rivet, la résistance au cisaillement et à la compression du rivet soumis à la force maximale peut être vérifiée séparément.
Exemple :
Une équerre reliée par un seul rivet est soumise à une force concentrée P, comme le montre la figure a. On sait que la force extérieure P est de 12 kN. Le diamètre du rivet est de 20 mm et chaque rivet est soumis à un cisaillement simple. Calculez la contrainte de cisaillement maximale sur la section transversale du rivet sous la force maximale.
Solution :
L'assemblage de rivets est symétrique par rapport à l'axe x, et le centre de rotation se trouve au point O, qui est le point d'intersection de la ligne reliant le rivet 2 et le rivet 5 avec l'axe x.
1. En simplifiant la force P au point O, on obtient :
P = 12 kN.
m=12 0,12=1,44KN.m
2. Sous l'action de la force P passant par le centre de rotation, et compte tenu du fait que chaque rivet a le même diamètre et le même matériau, la force exercée sur chaque rivet est égale.
3. Sous l'action du moment m, la force que supporte chaque rivet est proportionnelle à la distance du rivet au centre de rotation.
Selon l'équation d'équilibre :
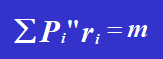
En résolvant l'équation, on obtient
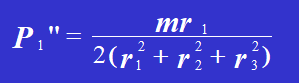
C'est pourquoi,
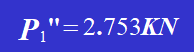
4. Dessinez le diagramme des forces de chaque rivet et combinez les vecteurs Pi' et Pi" pour obtenir la force de cisaillement totale agissant sur chaque rivet, y compris sa magnitude et sa direction. On peut conclure que le rivet 1 et le rivet 6 supportent la force maximale, la valeur de la force maximale étant :
La contrainte de cisaillement sur la section transversale du rivet est :
Vous trouverez ci-dessous les réponses à certaines questions fréquemment posées :
Dans la construction, différents types de rivets sont utilisés pour leurs propriétés et applications uniques. Les rivets pleins, également connus sous le nom de rivets ronds, sont le type le plus courant et le plus ancien ; ils se composent d'une tige solide et d'une tête. Ils sont installés en déformant la queue à l'aide d'un marteau ou d'un outil de sertissage et sont largement utilisés en raison de leur grande résistance et de leur fiabilité. Les rivets en acier de construction sont similaires aux rivets pleins, mais ils sont conçus pour des applications soumises à des contraintes élevées dans la construction commerciale, comme les ponts et les immeubles de grande hauteur.
Les rivets aveugles, ou rivets pop, sont des rivets tubulaires munis d'un mandrin en leur centre, installés à l'aide d'une riveteuse. Ils sont idéaux pour les applications où l'accès à la face arrière du joint est limité. Les rivets à enfoncer, semblables aux rivets aveugles, ne nécessitent pas d'outil spécial pour l'installation et sont enfoncés à l'aide d'un marteau. Ils conviennent aux applications où les trous ne pénètrent pas l'ensemble du panneau ou du bloc.
Les rivets affleurants, ou rivets à tête fraisée, ont des têtes et des trous fraisés, ce qui leur permet d'affleurer la surface, de réduire la traînée aérodynamique et d'obtenir une finition de surface lisse. Les rivets fendus, ou rivets bifurqués, présentent des extrémités pointues qui se fendent dans des directions opposées lorsqu'elles sont enfoncées dans un matériau, ce qui est idéal pour assembler des matériaux souples tels que le bois, le plastique et le cuir. Les rivets tubulaires sont creux, avec une tête à une extrémité et une queue à l'autre. Ils nécessitent moins de force pour être installés et sont utilisés dans les applications où les matériaux à fixer sont souples.
Les rivets sont fabriqués à partir de différents matériaux, notamment l'acier inoxydable, l'acier, l'aluminium, le laiton et le cuivre, chacun étant choisi en fonction des exigences spécifiques du projet. Ces matériaux offrent des caractéristiques différentes en termes de solidité, de résistance à la corrosion et de poids, ce qui rend les rivets polyvalents pour toute une série d'applications dans le domaine de la construction.
Lorsque l'on compare les assemblages rivetés aux assemblages soudés, plusieurs différences et considérations essentielles apparaissent. Les assemblages soudés offrent généralement une résistance et une capacité de charge plus élevées que les assemblages rivetés. Un joint soudé sain peut atteindre 100% de la résistance du matériau de base, alors que les joints rivetés ont une résistance plus faible en raison de la réduction de la section transversale causée par les trous percés pour les rivets.
En termes de conception et d'installation, le soudage est souvent plus simple et plus rapide car il ne nécessite pas de trous pré-percés ou de pièces supplémentaires comme les rivets. Le rivetage, en revanche, implique le perçage, la fixation et l'aplatissement des rivets, ce qui prend plus de temps et nécessite plus de main-d'œuvre.
Les performances en matière de vibrations et de fatigue diffèrent entre les deux méthodes. Les assemblages rivetés résistent mieux aux charges cycliques et aux vibrations car la déformation et l'expansion des rivets renforcent l'assemblage au fil du temps. Les joints soudés, bien que solides, peuvent être plus susceptibles de se dégrader sous l'effet de cycles de charge répétés.
En ce qui concerne les matériaux et leur compatibilité, le rivetage est plus polyvalent pour assembler des matériaux dissemblables, car il ne nécessite pas de tenir compte des points de fusion. Le soudage, en revanche, nécessite des matériaux dont les points de fusion et les propriétés thermiques sont compatibles.
D'un point de vue esthétique, les joints soudés peuvent offrir une finition de surface plus lisse après le post-traitement, ce qui est souvent plus agréable que les têtes de rivets visibles des joints rivetés.
En ce qui concerne l'entretien et le démontage, les assemblages rivetés sont plus faciles à démonter et à réparer car les rivets peuvent être percés et remplacés. Les joints soudés sont plus permanents et doivent être coupés et ressoudés pour être démontés, ce qui prend plus de temps et est plus coûteux.
En termes de poids et d'intégrité structurelle, les structures soudées sont généralement plus légères car elles ne nécessitent pas de matériaux supplémentaires tels que des rivets et des sangles. Les structures rivetées peuvent être plus lourdes en raison de ces composants supplémentaires.
Le coût et l'efficacité jouent également un rôle dans le choix entre les deux méthodes. Le rivetage a tendance à être plus coûteux dans l'ensemble, malgré le faible coût des rivets individuels, en raison de l'accumulation des coûts des matériaux, de l'exploitation et de la main-d'œuvre. Le soudage, en particulier avec des procédés automatisés, peut être plus rentable et plus rapide.
En résumé, le choix entre le rivetage et le soudage dépend des exigences spécifiques de l'application, y compris les besoins de résistance, la compatibilité des matériaux, les considérations esthétiques et les exigences de maintenance. Le soudage offre une plus grande résistance, une conception plus simple et une production plus rapide, mais il peut introduire une distorsion thermique et est moins flexible pour le démontage. Le rivetage offre une meilleure résistance aux vibrations, un démontage plus facile et la possibilité d'assembler des matériaux différents, mais il est généralement plus faible et demande plus de travail.
Les assemblages rivetés sont largement utilisés dans l'ingénierie moderne en raison de leur durabilité, de leur fiabilité et des avantages spécifiques qu'ils présentent par rapport à d'autres méthodes d'assemblage. Dans l'industrie aérospatiale, les joints rivetés sont essentiels pour relier des composants tels que les panneaux de fuselage et les ailes, où leurs caractéristiques de légèreté et de haute résistance sont essentielles pour maintenir l'intégrité structurelle tout en minimisant le poids. Dans la construction navale, les joints rivetés sont indispensables pour assembler les coques et d'autres pièces clés des navires. Ils offrent une résistance à la pression de l'eau et à la corrosion, ce qui est essentiel pour garantir l'intégrité de l'étanchéité et la sécurité dans les eaux agitées.
Dans les secteurs de la construction et de l'infrastructure, les joints rivetés sont utilisés dans des structures telles que les ponts, les tours et les bâtiments. Ces joints sont appréciés pour leur capacité à répartir uniformément les charges et à assurer la stabilité des grandes structures, ce qui les rend idéaux pour les applications qui nécessitent un support robuste, comme les poutres et les poutrelles des ponts. Pour les appareils à pression et les chaudières, les joints rivetés sont préférés lorsque les procédés thermiques tels que le soudage ne sont pas pratiques ou lorsque les joints doivent résister aux fluctuations de température et aux vibrations.
Les industries de l'automobile et des transports publics bénéficient également des joints rivetés, notamment dans la fabrication des carrosseries d'autobus et de trolleybus. Ces joints assurent des connexions solides et fiables, capables de résister aux contraintes et aux vibrations associées à ces véhicules. En outre, on trouve des joints rivetés dans des produits de consommation tels que les ustensiles de cuisine et les couteaux de poche, où leur solidité, leur légèreté et leur résistance à la corrosion sont avantageuses.
Globalement, les assemblages rivetés sont privilégiés dans les environnements soumis à des vibrations ou à des charges dynamiques en raison de leur résistance au desserrage dans le temps. Ils conviennent également aux industries soumises à des fluctuations de température, car leur installation ne nécessite pas de chaleur et ils sont résistants à la dilatation thermique. En outre, les assemblages rivetés sont plus faciles à inspecter et à démonter que les assemblages soudés, ce qui endommage moins les pièces concernées. Ces caractéristiques font des joints rivetés une méthode privilégiée dans diverses industries critiques et de haute performance.
Les assemblages rivetés présentent plusieurs avantages et inconvénients, ce qui les rend adaptés à des applications spécifiques tout en posant des problèmes dans d'autres cas.
Les assemblages rivetés présentent l'avantage d'être rentables, car les rivets sont peu coûteux et ne nécessitent pas d'électricité ou de matériaux spéciaux, ce qui permet d'économiser sur les coûts des matériaux et de l'énergie. Le rivetage augmente également le rendement de la production, car il nécessite généralement moins d'équipement et de préparation que le soudage, ce qui réduit le temps et les ressources nécessaires. Le processus génère un minimum de déchets, ce qui améliore l'efficacité. Les assemblages rivetés offrent une grande souplesse de conception et sont plus faciles à inspecter et à entretenir ; les rivets usés peuvent être rapidement remplacés avec un minimum d'équipement. Ils sont polyvalents, capables d'assembler des métaux ferreux et non ferreux, ainsi que des matériaux non métalliques tels que le bois, le plastique et les feuilles d'amiante. Le rivetage est respectueux de l'environnement et de l'utilisateur, car il ne produit ni fumées ni gaz, ce qui le rend plus sûr pour les travailleurs. En outre, les joints rivetés offrent une grande résistance au cisaillement et une bonne résistance à la fatigue, ce qui convient aux applications soumises à des vibrations et à des forces d'impact.
Cependant, les connexions rivetées présentent également des inconvénients. Ils nécessitent une main-d'œuvre plus importante, impliquant plusieurs étapes telles que le perçage des trous et l'installation des rivets, ce qui peut augmenter les coûts de main-d'œuvre. Les rivets ajoutent du poids à la structure, ce qui peut être important dans les grandes structures et peut affecter l'efficacité de la structure. Les trous nécessaires à la pose des rivets peuvent affaiblir les plaques métalliques, entraînant une concentration des contraintes autour des trous, ce qui peut nécessiter une épaisseur supplémentaire ou un chevauchement des plaques pour maintenir l'intégrité de la structure. D'un point de vue esthétique, les assemblages rivetés sont plus visibles et peuvent dépasser de la structure, ce qui réduit l'attrait visuel par rapport aux assemblages soudés. Le rivetage peut être bruyant pendant l'installation et peut être sujet à la corrosion s'il n'est pas correctement scellé, ce qui augmente les coûts d'entretien au fil du temps. Les joints rivetés peuvent ne pas être étanches à moins d'utiliser des rivets chauds ou des produits d'étanchéité, ce qui peut être un inconvénient dans certaines applications. Enfin, si les rivets peuvent être remplacés, le processus peut être encombrant et bruyant, et le remplacement des rivets pendant la maintenance peut s'avérer plus difficile que d'autres méthodes de fixation comme les boulons.
En résumé, les assemblages rivetés sont rentables et flexibles, mais ils s'accompagnent d'une main-d'œuvre plus importante, d'un poids structurel plus élevé, de problèmes de concentration de contraintes et de limitations esthétiques. Le choix entre le rivetage et d'autres méthodes d'assemblage dépend des exigences spécifiques du projet.
L'entretien et la réparation efficaces des assemblages rivetés impliquent plusieurs étapes cruciales pour garantir l'intégrité et la longévité de la structure. Une inspection régulière est essentielle ; vérifiez que les joints rivetés ne présentent pas de signes d'usure, de corrosion ou de fatigue. Nettoyez périodiquement les assemblages pour éliminer les débris, la saleté ou les substances corrosives qui pourraient compromettre l'assemblage. Pour le nettoyage des pistolets à rivets pneumatiques utilisés pour la maintenance, il faut veiller à nettoyer, lubrifier et inspecter soigneusement les tuyaux d'air et les raccords afin d'éviter tout dysfonctionnement.
En ce qui concerne les réparations, commencez par identifier les défauts tels que la taille incorrecte des rivets ou la mauvaise préparation des trous. Si les rivets doivent être remplacés, il faut les retirer avec précaution en perçant la tête et en utilisant un chasse-goupille pour casser la tige sans endommager le matériau environnant. Remplacez toujours les rivets par des rivets de la bonne taille et du bon type, en veillant à utiliser les bonnes techniques de pose pour éviter les problèmes tels que les têtes inclinées ou les fissures.
Des techniques spécialisées telles que le bobinage, le frenching et le soudage en anneau peuvent être utilisées pour des réparations plus importantes, en particulier pour les rivets anciens ou très endommagés. Il est également essentiel de remédier à toute corrosion potentielle en scellant correctement les joints, en particulier lorsque des métaux différents sont en jeu, afin d'éviter la corrosion galvanique.
Veillez à ce que les assemblages rivetés ne soient pas soumis à une fatigue et à des vibrations excessives, qui peuvent entraîner des défaillances. Éviter toute compression excessive lors de l'installation afin d'empêcher la formation de vides ou le durcissement du métal. Après les réparations, procédez à des essais et à des inspections approfondis pour confirmer l'intégrité structurelle et l'étanchéité des joints. Remédiez rapidement aux fuites éventuelles en procédant à un calfeutrage supplémentaire ou en ajustant les rivets.
En suivant ces conseils d'entretien et de réparation, vous pourrez maintenir la solidité, la fiabilité et la sécurité de vos assemblages rivetés au fil du temps.
En tant que fondateur de MachineMFG, j'ai consacré plus d'une décennie de ma carrière à l'industrie métallurgique. Ma vaste expérience m'a permis de devenir un expert dans les domaines de la fabrication de tôles, de l'usinage, de l'ingénierie mécanique et des machines-outils pour les métaux. Je suis constamment en train de réfléchir, de lire et d'écrire sur ces sujets, m'efforçant constamment de rester à la pointe de mon domaine. Laissez mes connaissances et mon expertise être un atout pour votre entreprise.
FR 
EN 
AR 
DE 
ES 
ID 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO 
TR