Vous êtes-vous déjà demandé ce qu'est un cercle parfait ? Dans le monde de l'ingénierie mécanique, la circularité est un concept crucial qui affecte les performances et la longévité des composants rotatifs. Cet article se penche sur les subtilités de la circularité, en explorant sa définition, les méthodes de mesure et les facteurs qui l'influencent. Que vous soyez un ingénieur chevronné ou un apprenant curieux, la compréhension de la circularité est essentielle à la conception et à l'entretien des machines de haute précision.
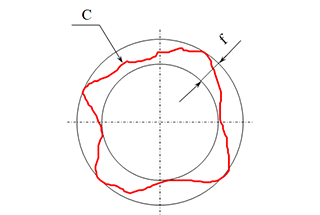
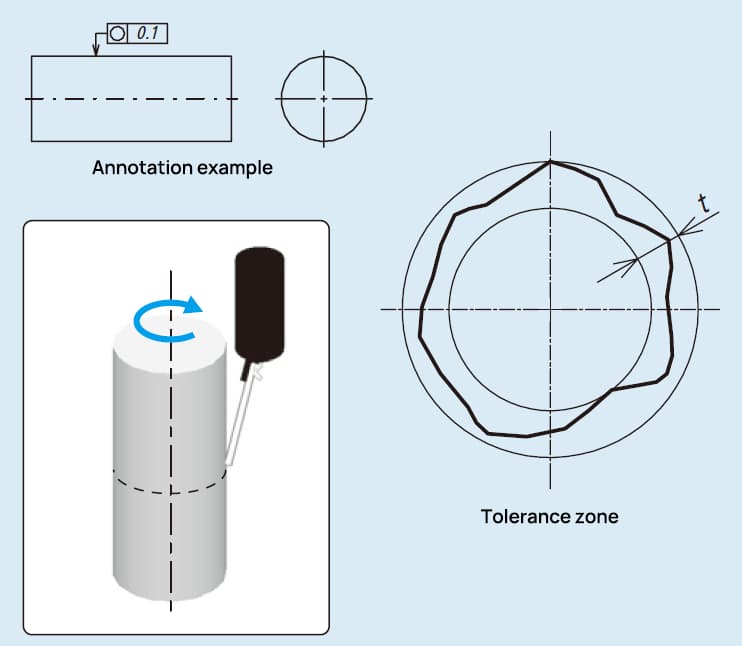
Dans la norme industrielle japonaise (JIS) B0621-1984, qui porte sur la définition et l'expression des écarts de forme et de position, la rondeur est définie comme "l'écart par rapport au cercle géométrique d'un corps circulaire". Cette norme fournit une méthode précise pour représenter la circularité, ce qui est crucial pour garantir la qualité et la fonctionnalité des composants circulaires dans l'ingénierie mécanique.
La représentation de la rondeur dans la norme JIS B0621-1984 est la suivante :
Pour les composants rotatifs, il est essentiel d'évaluer leur véritable forme circulaire afin de garantir leur bon fonctionnement et leur longévité. La préoccupation immédiate est de déterminer la tolérance de circularité, qui est l'écart admissible par rapport à un cercle parfait. Cette évaluation commence par :
La tolérance de circularité est une spécification de dimensionnement et de tolérancement géométrique (GD&T) qui définit l'écart admissible par rapport à un cercle parfait dans un plan de coupe transversale d'une pièce cylindrique ou sphérique. Elle garantit que la circonférence mesurée d'une pièce se situe à l'intérieur d'une zone de tolérance spécifiée, qui est la zone comprise entre deux cercles concentriques de même section avec une différence de rayon t. Cette zone de tolérance garantit que la pièce conserve une forme circulaire cohérente dans les limites définies.
Imaginez une coupe transversale d'une pièce cylindrique. La zone de tolérance de circularité est représentée par la zone comprise entre deux cercles concentriques. La différence de rayon t entre ces cercles représente l'écart admissible par rapport à la forme circulaire idéale. Tout point de la circonférence réelle de la pièce doit se situer à l'intérieur de cette zone pour satisfaire à l'exigence de tolérance de circularité.
Plusieurs facteurs peuvent entraîner des écarts de circularité et de cylindricité qui affectent la précision et la fonctionnalité des pièces usinées. Voici les causes les plus courantes :
Il existe plusieurs méthodes d'évaluation de la circularité, chacune ayant ses propres caractéristiques et avantages. La méthode à utiliser est généralement choisie en fonction des exigences spécifiques de la pièce à usiner.
Par exemple :
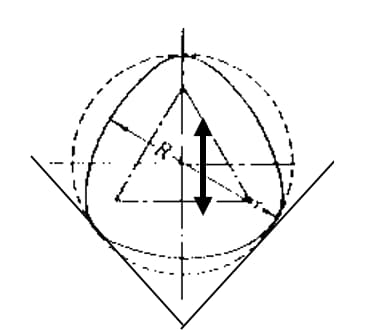
Méthode du diamètre
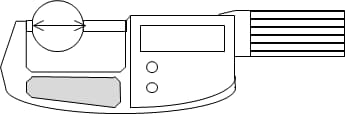
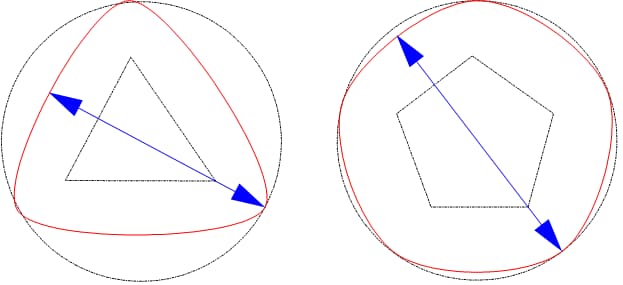
La circularité peut être mesurée directement à l'aide d'outils tels que les micromètres. Cette méthode est simple et facile à mettre en œuvre. Toutefois, lors de l'évaluation de cercles triangulaires et pentagonaux de même diamètre, il est facile de les mesurer comme étant circulaires alors qu'ils ne le sont pas, ce qui conduit à des résultats erronés.
Méthode des trois points
La méthode des trois points permet d'obtenir des données sur la circularité par le biais de [bloc en V + micromètre / mètre + banc].
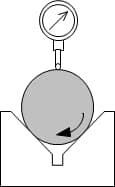
Toutefois, la méthode des trois points peut donner lieu à des mesures incorrectes en raison des différences de la ligne tangente au point d'appui sélectionné et des difficultés à déterminer le centre du point de référence. En outre, des erreurs peuvent se produire pendant la mesure en raison du mouvement de haut en bas avec la rotation de l'objet mesuré.
Par exemple :
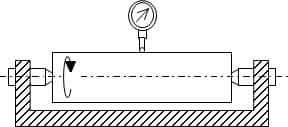
Méthode du rayon
La méthode du rayon évalue la rondeur en utilisant la différence entre le rayon maximal et minimal obtenu après avoir fait tourner la pièce pendant un cycle. Comme le montre la figure, les résultats des mesures peuvent également être facilement influencés par l'horizontalité de la pièce.
La zone de tolérance est comprise entre deux cercles concentriques sur la même section.
Méthode centrale
Par rapport à la méthode centrale, la méthode du rayon est surtout utilisée pour des mesures plus précises. Les données de détection de la circularité dépendent du cercle de référence. Différentes méthodes d'évaluation du cercle d'essai entraîneront différentes positions centrales du cercle de référence, ce qui affectera la position axiale de la caractéristique circulaire mesurée.
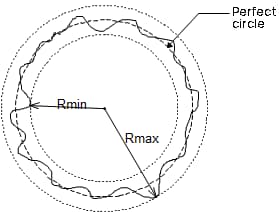
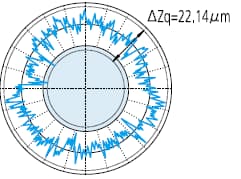
Pour déterminer la rondeur, le contour mesuré est ajusté à un cercle et la somme des carrés de la déviation des données du contour par rapport au cercle est minimisée. La valeur de la rondeur est alors définie comme la différence entre l'écart maximal (de la valeur maximale à la valeur minimale) du contour et du cercle.
ΔZｑ=Rmax-Rmin, symbole représentant la valeur de l'arrondi par le LSC
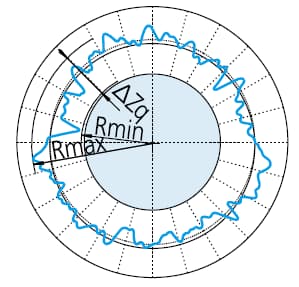
Pour minimiser la différence radiale, deux cercles concentriques sont placés autour du contour mesuré. La valeur de la rondeur est définie comme l'intervalle radial entre les deux cercles.
ΔZｚ=Rmax-Rmin , symbole représentant la valeur de l'arrondi par MZC
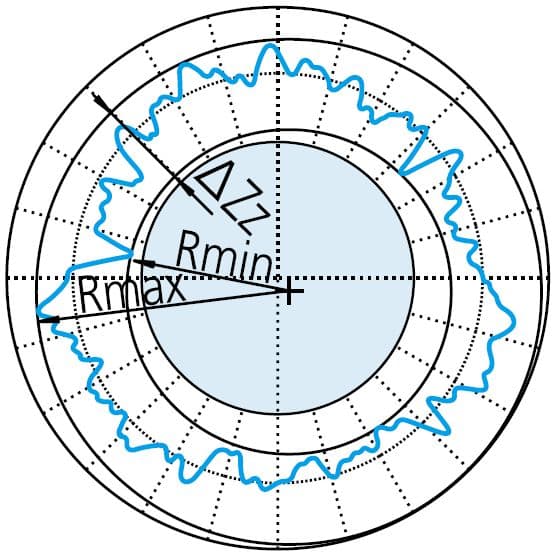
Tout d'abord, il faut créer le plus petit cercle qui entoure le profil mesuré. Ensuite, la valeur de circularité est définie comme l'écart maximal entre le contour et le cercle. Cette méthode est couramment utilisée pour évaluer les arbres, les tiges et autres objets similaires.
ΔZｃ=Rmax-Rmin , le symbole de la valeur de l'arrondi par le biais du MCC.
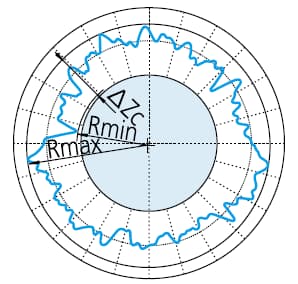
Créez le plus grand cercle pouvant contenir le profil mesuré. Ensuite, la valeur de circularité est définie comme l'écart maximal entre le contour et le cercle.
ΔZｉ=Rmax-Rmin , le symbole indiquant la valeur de l'arrondi par le biais du MIC.
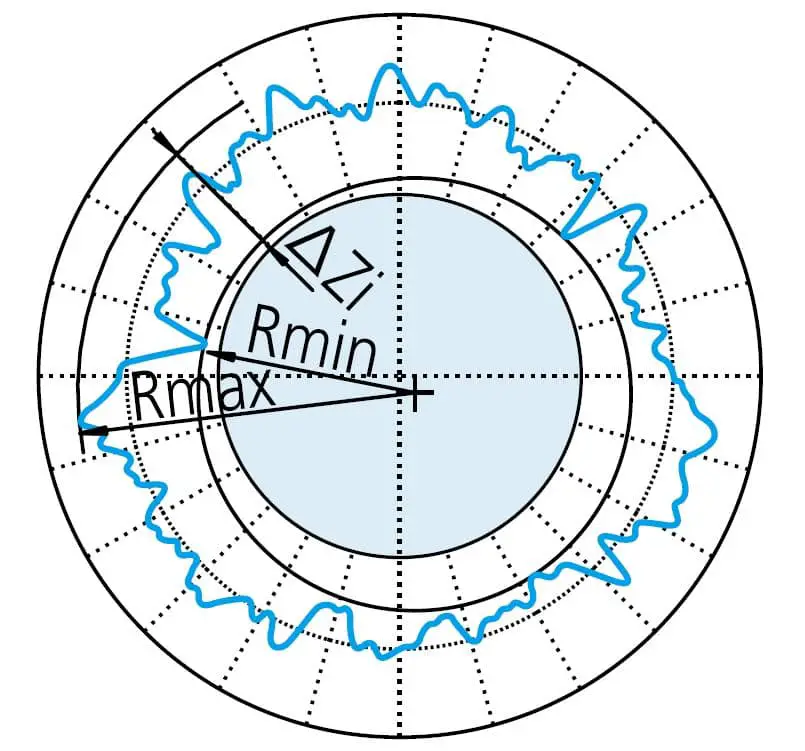
Lors de l'évaluation de la rondeur, le contour obtenu est généralement filtré afin de réduire ou d'éliminer l'influence des bruits inutiles.
Les méthodes de filtrage et les valeurs limites de filtrage définies (UPR : fluctuations par tour) peuvent varier en fonction des exigences de mesure spécifiques. La figure ci-dessous illustre les effets variables des réglages du filtre sur le contour mesuré.
Pas de filtre :
Filtre passe-bas :
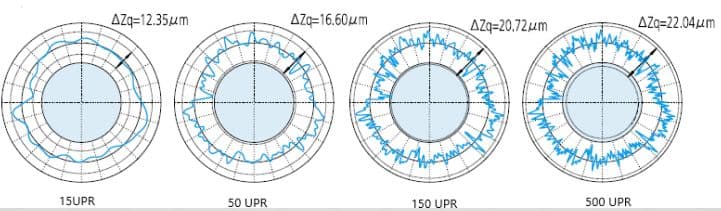
Filtre passe-bande :
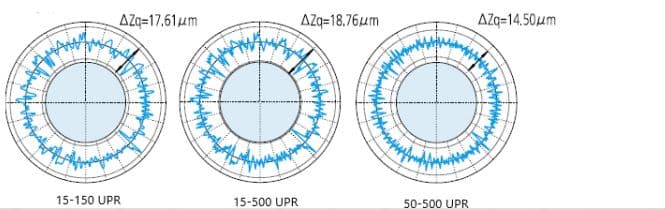
En tant qu'évaluateurs, que peuvent nous apprendre ces chiffres ?
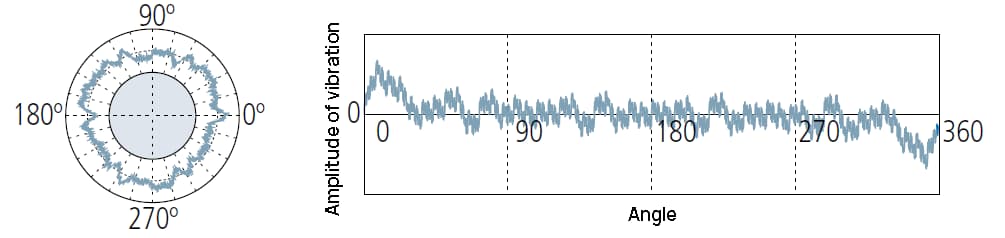
Figure : tableau des résultats des mesures
1 UPR : une seule onde est conservée après le filtrage :
1La composante UPR indique l'excentricité de la pièce par rapport à l'axe de rotation de l'instrument de mesure.
L'amplitude de la forme d'onde dépend du réglage de son niveau.
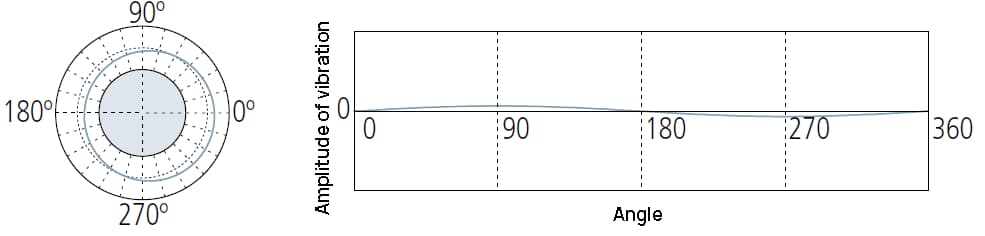
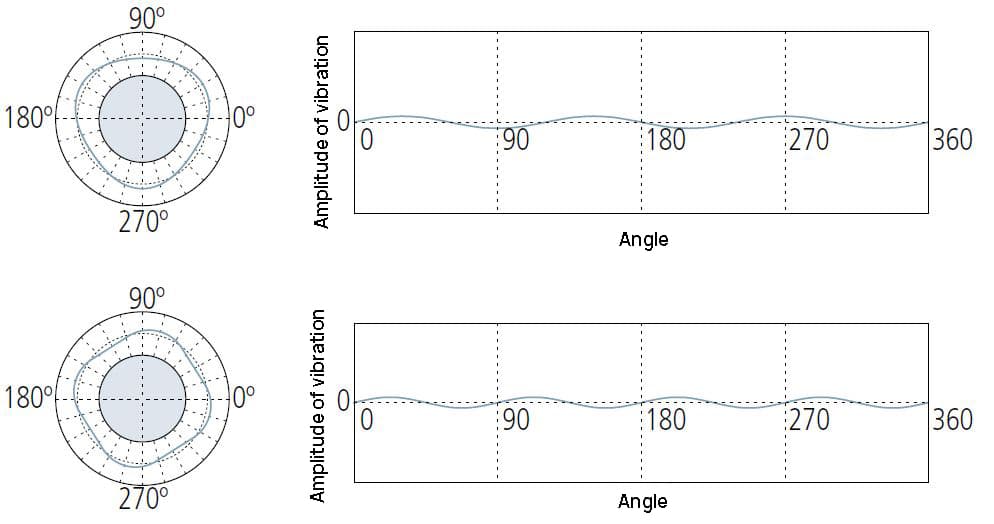
Les composants du 2UPR peuvent indiquer :
① Réglage insuffisant du niveau des instruments de mesure ;
② Battement circulaire causé par une mauvaise installation de la pièce sur la machine-outil qui lui donne sa forme ;
③ La forme de la pièce à usiner est ovale, par exemple dans le piston d'un moteur à combustion interne.
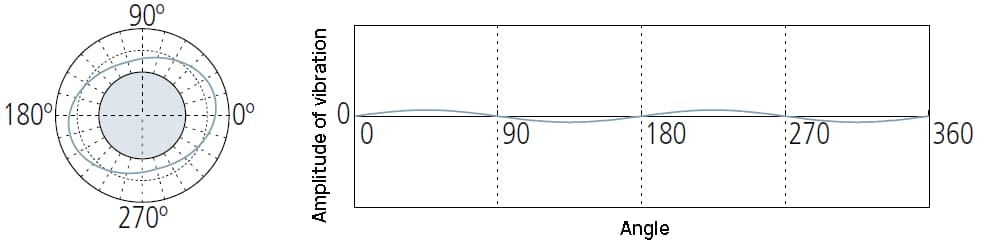
Peut indiquer :
① Déformation due à un serrage trop important de la pince de maintien de l'instrument de mesure.
② Déformation de relaxation causée par la libération de la contrainte lors du déchargement du mandrin fixe de la machine-outil d'usinage.
Il s'agit généralement de facteurs déséquilibrés dans la méthode de traitement ou le processus de production des pièces.
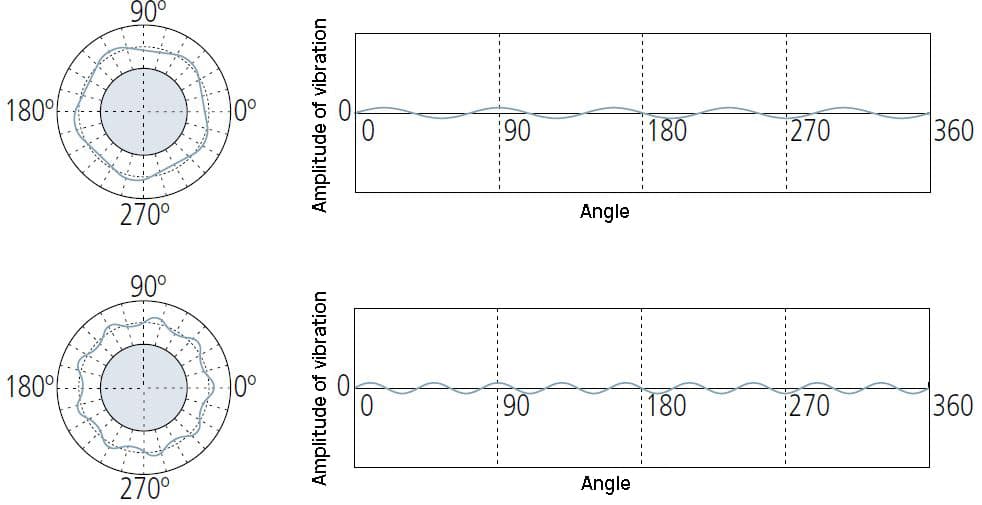
15 conditions UPR (ou plus) sont généralement dues à leurs propres causes, telles que le broutage de l'outil, les vibrations de la machine, l'effet de transfert du liquide de refroidissement, l'inhomogénéité du matériau, etc.
| Paramètres | Signification |
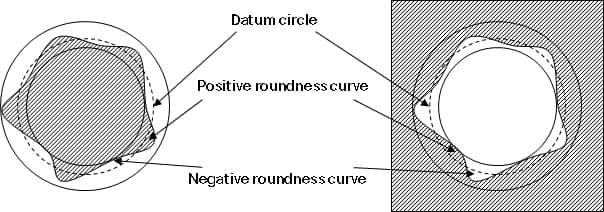
| RONt | La valeur mesurée de l'arrondi représente la différence entre la valeur maximale de la courbe d'arrondi positive et la valeur minimale de la courbe d'arrondi négative ou la somme des valeurs absolues. |
| RONp | La hauteur de crête mesurée de la courbe d'arrondi représente la valeur maximale de la courbe d'arrondi positive. |
| RONV | La valeur mesurée de l'arrondi représente la valeur absolue de la valeur minimale de la courbe négative de l'arrondi. |
| RONq | La mesure de l'arrondi à double racine carrée moyenne représente la double racine carrée moyenne de la courbe d'arrondi. |
Enfin, voyons quels sont les outils et instruments disponibles pour mesurer la rotondité.
Micromètre :
Instrument de mesure de la circularité :
Machine à mesurer tridimensionnelle :
L'espace étant limité, vous pouvez laisser un message et critiquer les sujets non traités.
Après avoir lu cet article, j'espère que vous avez acquis une meilleure compréhension de la notion de rondeur. Si vous avez d'autres questions, n'hésitez pas à laisser un commentaire ci-dessous.
En tant que fondateur de MachineMFG, j'ai consacré plus d'une décennie de ma carrière à l'industrie métallurgique. Ma vaste expérience m'a permis de devenir un expert dans les domaines de la fabrication de tôles, de l'usinage, de l'ingénierie mécanique et des machines-outils pour les métaux. Je suis constamment en train de réfléchir, de lire et d'écrire sur ces sujets, m'efforçant constamment de rester à la pointe de mon domaine. Laissez mes connaissances et mon expertise être un atout pour votre entreprise.
FR 
EN 
AR 
DE 
ES 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO