Comment mesurer la rectitude d'un rail de guidage pour garantir la précision des opérations de la machine ? Cet article examine deux méthodes courantes : la méthode de raccordement des deux extrémités et la méthode des conditions minimales. En comparant ces techniques, vous apprendrez comment chacune évalue les erreurs de rectitude et pourquoi le choix de la bonne méthode est crucial pour obtenir des mesures précises. Plongez dans cet article pour comprendre les avantages et les inconvénients de chaque approche, et découvrez quelle méthode répond le mieux à vos besoins pour obtenir une rectitude optimale dans vos projets d'ingénierie.
Dans la pratique, il existe deux méthodes couramment utilisées pour évaluer l'erreur de rectitude des rails de guidage : la méthode de raccordement des deux extrémités et la méthode des conditions minimales.
La méthode de connexion à deux points d'extrémité relie la courbe d'erreur d'un bout à l'autre, puis trace deux lignes parallèles à la ligne d'extrémité aux points les plus élevés et les plus bas de la courbe, et mesure les valeurs le long de l'axe vertical entre les deux lignes parallèles.
Après traitement des données, la valeur obtenue correspond à l'erreur de rectitude du rail de guidage.
La méthode des conditions minimales relie les points "haut, haut" (ou "bas, bas") de la courbe d'erreur et trace une ligne parallèle qui passe par le point bas (haut).
La valeur mesurée entre les deux lignes parallèles le long de l'axe vertical est l'erreur de rectitude du rail de guidage après traitement des données.
La méthode de la condition minimale est une évaluation d'arbitrage.
La méthode de connexion à deux points d'extrémité n'est pas une évaluation d'arbitrage, mais elle est couramment utilisée dans la production en raison de sa simplicité et de sa commodité d'évaluation, bien qu'elle puisse parfois produire des erreurs importantes.
Cet article traite de la valeur limite de l'erreur générée entre ces deux méthodes d'évaluation.
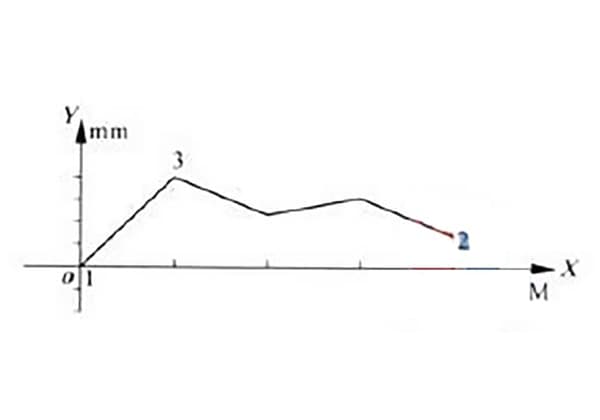
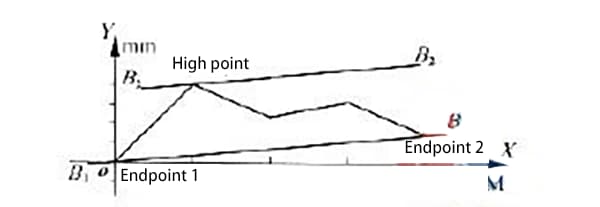
En mesurant l'erreur de rectitude d'un certain modèle de guide hydraulique à glissière, la courbe d'erreur de rectitude a été obtenue comme le montre la figure 1.
Comme le montre la figure, la courbe d'erreur se trouve du même côté que les deux extrémités de la ligne.
Ci-dessous, la valeur de l'erreur de rectitude du rail de guidage sera évaluée à l'aide de la méthode des conditions minimales et de la méthode de connexion à deux extrémités.
(1) Évaluation de l'erreur de rectitude à l'aide de la méthode des conditions minimales
Selon la méthode des conditions minimales, les points les plus bas 1 et 2 de la courbe de la figure 1 (le point bas 1 coïncidant avec l'origine) sont reliés par la ligne a1a1, comme le montre la figure 2.
La droite parallèle a2a2 passe par le point le plus élevé 3 par rapport à la droite a1a1.
La valeur mesurée le long de l'axe y dans la région délimitée par les deux lignes parallèles a1a1 et a2a2, après traitement des données, représente l'erreur de rectitude du rail de guidage δ obtenue par la méthode des conditions minimales.
(2) Évaluation de l'erreur de rectitude à l'aide de la méthode de connexion à deux extrémités
Selon la méthode de connexion à deux extrémités, les extrémités de la courbe de la figure 1 sont également les points d'extrémité 1 et 2 de la courbe, comme le montre la figure 3.
Les points extrêmes 1 et 2 sont reliés par la ligne b1b1, puis une ligne parallèle b2b2 est tracée à travers le point le plus élevé.
La valeur mesurée le long de l'axe y dans la région délimitée par les deux lignes parallèles b1b1 et b2b2, après traitement des données, représente l'erreur de rectitude du rail de guidage δ obtenue à partir de la méthode de connexion à deux extrémités.
(3) Détermination de la limite d'erreur générée par les deux méthodes d'évaluation
Comme les deux méthodes d'évaluation sont utilisées pour déterminer l'erreur de rectitude du même rail de guidage, le "point bas 1", le "point bas 2" et le "point haut 3" de la figure 2 correspondent respectivement au "point final 1", au "point final 2" et au "point haut 3" de la figure 3. La ligne a1a1 coïncide donc avec la ligne b1b1, et la ligne a2a2 coïncide avec la ligne b2b2.
Par conséquent, la valeur de l'erreur générée par les deux méthodes d'évaluation est nulle.
Sur la base de l'analyse ci-dessus, lorsque la courbe d'erreur est du même côté que les deux extrémités de la ligne, la limite d'erreur générée par les deux méthodes d'évaluation est nulle, ce qui signifie que les résultats d'évaluation obtenus par les deux méthodes sont identiques.
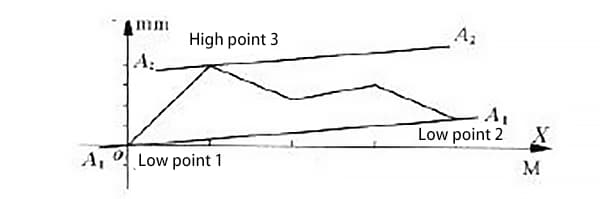
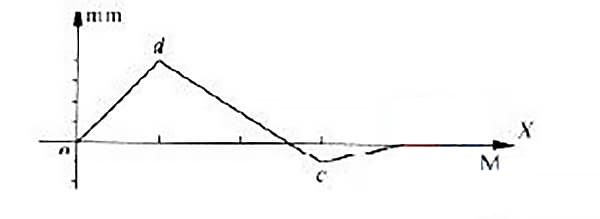
Dans la courbe d'erreur de rectitude mesurée d'un rail de guidage, certaines courbes d'erreur se trouvent des deux côtés de la ligne reliant les extrémités, comme le montre la figure 4.
La courbe d'erreur de ce rail de guidage a une ligne reliant ses extrémités et coïncidant avec l'axe x. L'erreur de rectitude du rail de guidage sera évaluée à l'aide de la méthode des conditions minimales et de la méthode de connexion à deux extrémités.
Comme le montre la figure 4, les points o et c sont les deux points bas et les deux extrémités de la courbe, tandis que le point d est le point le plus élevé.
Selon la méthode des conditions minimales, les points o et c sont reliés par la ligne a1a1, comme le montre la figure 5. La ligne a2a2 est tracée parallèlement à la ligne a1a1 et passe par le point le plus élevé d.
La valeur mesurée le long de l'axe y dans la région délimitée par les deux lignes parallèles a1a1 et a2a2, après traitement des données, représente l'erreur de rectitude du rail de guidage δ obtenue par la méthode des conditions minimales.
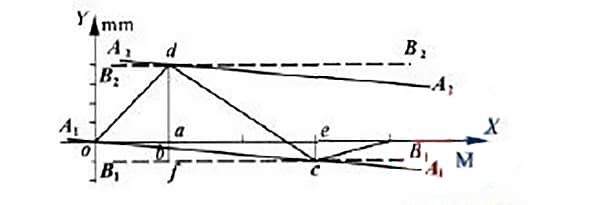
Selon la méthode du raccordement en deux points, tracer deux droites parallèles à l'axe des abscisses passant respectivement par les points C et D.
Ces lignes sont représentées par les lignes pointillées b1b1 et b2b2 dans la figure 5. Dans la région délimitée par ces deux lignes parallèles, la valeur mesurée le long de l'axe y, après traitement des données, représente la valeur de l'erreur de rectitude du rail de guidage entre les deux points d'extrémité.
Pour déterminer la méthode de l'écart minimal et la valeur de l'écart aux deux points extrêmes, tracer une ligne parallèle à l'axe des y passant par le point D, coupant l'axe au point A, coupant la ligne a1a1 au point H et coupant la ligne b1b1 au point F.
De même, tracez une ligne parallèle à l'axe des ordonnées passant par le point C et coupant l'axe au point E.
(1) Détermination de l'erreur de rectitude par la méthode des conditions minimales
Selon la méthode des conditions minimales, la valeur de l'erreur de rectitude δ du rail de guidage est dérivée de la valeur mesurée le long de l'axe y après le traitement des données, ce qui représente la méthode de l'écart minimal.
Comme le montre la figure 5 :
Et puisque BD = BA + AD,
∆OAB et ∆OEC sont donc deux triangles semblables,
En réarrangeant l'équation (3), nous obtenons :
En substituant l'équation (4) à l'équation (2) et en réarrangeant, nous obtenons :
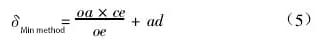
(2) Détermination de l'erreur de rectitude à l'aide de la méthode de connexion à deux points
Selon la méthode de raccordement en deux points, la valeur mesurée le long de l'axe y après traitement des données représente la valeur de l'erreur de rectitude δ du rail de guidage entre les deux points d'extrémité.
Comme le montre la figure 5 :
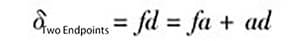
Et puisque fa = ce,
(3) Calcul des valeurs d'erreur générées par deux méthodes d'évaluation
Équation (6) moins équation (5), c'est-à-dire,
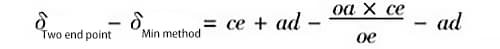
En réarrangeant, on obtient
(4) Calcul de l'erreur maximale générée par deux méthodes d'évaluation
Dans la figure 5, notons ad = δ1, ce = δ2, oa = p ; notons que la longueur du rail de guidage mesuré est l, alors oe = l - p, et.. :
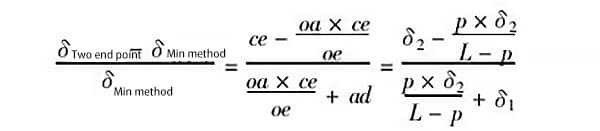
Par exemple, lorsque p = 0,5m (c'est-à-dire que le pas est de 0,5m), δ1 = 1,0δ, δ2 = 0,25δ, et que la longueur du rail de guidage mesuré est l - 2m, le rapport d'erreur généré par les deux méthodes d'évaluation est le suivant :
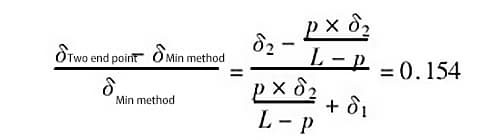
Le ratio de l'erreur générée par les deux méthodes d'évaluation est de 0,154, ce qui signifie que l'erreur générée par la méthode de connexion en deux points est supérieure de 15,4% à celle générée par la méthode des conditions minimales.
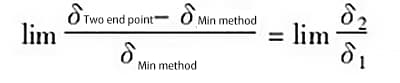
Dans l'équation ci-dessus, lorsque 
c'est-à-dire que les points les plus élevés et les plus bas de la courbe d'erreur sont infiniment éloignés l'un de l'autre, alors
, ce qui nous permet d'obtenir :
Par exemple, lorsque δ1 = 1,0δ et δ2 = 0,25δ et que la distance entre les points les plus élevés et les plus bas de la courbe d'erreur est infiniment éloignée (c'est-à-dire L=0,25), le rapport d'erreur généré par les deux méthodes d'évaluation est le suivant 
ce qui signifie que l'erreur générée par la méthode de connexion à deux points est 25% plus importante que celle générée par la méthode des conditions minimales.
Lorsque δ1 = δ2, c'est-à-dire lorsque la distance entre les points les plus élevés et les plus bas de la courbe d'erreur est égale, comme le montre la figure 6, les valeurs d'erreur maximales générées par les deux méthodes d'évaluation sont les suivantes :
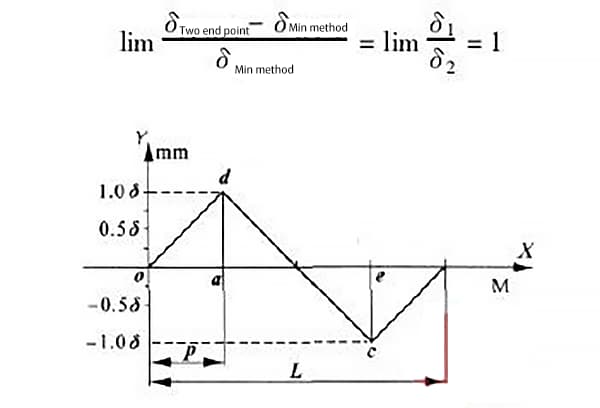
Il en ressort que lorsque les points les plus hauts et les plus bas du rail de guidage sont égaux et infiniment éloignés, l'erreur maximale générée par les deux méthodes d'évaluation est la plus importante et peut atteindre 100%.
Le tableau 1 présente le rapport des erreurs générées par les deux méthodes d'évaluation pour différentes longueurs du rail de guidage mesuré, lorsque les points de la courbe d'erreur sont répartis de part et d'autre de la ligne de connexion à deux points.
La distance entre le point le plus haut et le point le plus bas de la courbe d'erreur est égale lorsque le pas de mesure p = 0,5.
Tableau 1 Taux d'erreur des deux méthodes d'évaluation
| Taux d'erreur | Distance L (M) entre le point le plus haut et le point le plus bas du rail de guidage | ||||||
| 1 | 10 | 15 | 20 | 25 | 30 | 40 | ∞ |
 | 33.30% | 90% | 93.30% | 95% | 96% | 96.70% | 97.50% |
Si les points de la courbe d'erreur de rectitude se trouvent du même côté de la ligne de jonction à deux points, les erreurs générées par les deux méthodes d'évaluation sont nulles, c'est-à-dire que les résultats obtenus par les deux méthodes d'évaluation sont identiques.
Si les points de la courbe d'erreur de rectitude se trouvent de part et d'autre de la ligne de raccordement en deux points, et si les points les plus élevés et les plus bas de la courbe d'erreur sont égaux et infiniment éloignés, l'erreur maximale générée par les deux méthodes d'évaluation est la plus importante, et l'erreur générée par la méthode de raccordement en deux points peut être 100% plus élevée que celle générée par la méthode des conditions minimales.
Par conséquent, lors de l'évaluation de l'erreur de rectitude des rails de guidage des grandes machines-outils dans la production pratique, il est très important de choisir la méthode d'évaluation appropriée. Lorsque les points de la courbe d'erreur se trouvent de part et d'autre de la ligne de connexion à deux points, la méthode des conditions minimales doit être utilisée comme premier choix pour l'évaluation.
En tant que fondateur de MachineMFG, j'ai consacré plus d'une décennie de ma carrière à l'industrie métallurgique. Ma vaste expérience m'a permis de devenir un expert dans les domaines de la fabrication de tôles, de l'usinage, de l'ingénierie mécanique et des machines-outils pour les métaux. Je suis constamment en train de réfléchir, de lire et d'écrire sur ces sujets, m'efforçant constamment de rester à la pointe de mon domaine. Laissez mes connaissances et mon expertise être un atout pour votre entreprise.
FR 
EN 
AR 
DE 
ES 
ID 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO 
TR