Imaginez que vous vous trouviez sur un pont et que vous regardiez passer un poids lourd. Vous êtes-vous déjà demandé pourquoi le pont ne s'effondre pas sous le poids ? Cet article se penche sur les concepts de déformation et de contrainte, expliquant comment les matériaux se déforment sous l'effet d'une force et comment les ingénieurs calculent ces déformations pour garantir la sécurité. Vous apprendrez les relations fondamentales entre ces forces, comment elles sont mesurées et leurs implications pratiques dans les structures de tous les jours. Que vous soyez un ingénieur en herbe ou un simple curieux, ce guide vous éclairera sur les forces invisibles qui maintiennent notre monde intact.

Tout d'abord, la majorité des entreprises de contrôle de la sécurité mesurent la déformation de la structure testée. Une déformation trop importante peut provoquer des accidents.
Par exemple, les fissures dans les structures, l'enfoncement et le déplacement entre la structure et une référence fixe sont des déformations importantes visibles à l'œil nu, qui peuvent être mesurées en millimètres à l'aide de jauges telles que les jauges de fissures, les niveaux statiques et les jauges de déplacement.
Mais comment représenter la petite déformation causée par la compression à l'intérieur de la structure testée ou la flexion à l'extérieur de l'objet en forme de poutre ?
La réponse est la tension.

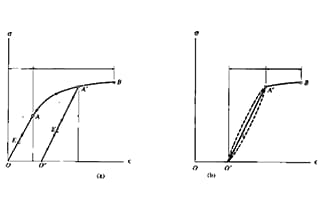
Supposons que la longueur d'une structure de longueur L subisse une déformation sous l'effet d'une contrainte et que sa longueur passe à L', alors sa variation de longueur ΔL = L' - L, et la déformation ε est le rapport entre la variation de longueur ΔL et la longueur originale L, la formule est la suivante :

Quelle est donc l'unité de contrainte ?
Comme le montre la formule, la déformation est un rapport et est sans dimension, c'est-à-dire qu'elle n'a pas d'unité.
Qu'est-ce que la microtension ?
Étant donné que ΔL est très petit, généralement de l'ordre du micron, la valeur de contrainte calculée est très petite, avec de nombreuses décimales, ce qui la rend peu pratique à afficher et à visualiser, de sorte que la notation scientifique 10-6 est introduite, appelée microcontrainte με, qui peut être comprise comme l'unité de microcontrainte est 10-6, et notre gamme de mesure de jauge de contrainte est de ±1500 microcontraintes, le positif indiquant l'étirement, et le négatif indiquant la compression.
La déformation est une petite déformation à l'intérieur de la structure testée. Pourquoi se déforme-t-elle ? Parce qu'elle est soumise à une force extérieure.
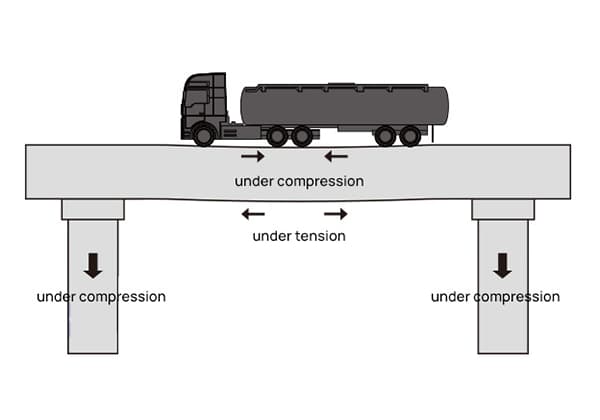
Si l'on prend l'exemple d'une pile de pont, si un camion entièrement chargé roule sur le pont, la pile supportera une pression supplémentaire et produira une compression et une déformation par compression, tandis que la pile produira une force interne pour contrebalancer la force externe et surmonter la déformation.
Cette force interne est une contrainte. La contrainte est définie comme la force par unité de surface, qui est en fait une pression, avec des unités de MPa.
Quelle est donc la relation entre la variable de déformation et la variation de la contrainte subie ? Voir la formule de calcul :

Dans la formule, σ représente la contrainte, E le module d'élasticité du matériau testé, également connu sous le nom de module de Young, qui est une quantité physique décrivant l'élasticité du matériau.
Elle peut être considérée comme la capacité du matériau à résister à la déformation (rigidité) et, d'un point de vue microéconomique, il s'agit de la force de liaison entre les atomes et les molécules.
Deux matériaux ayant la même déformation (la même valeur de contrainte), le matériau ayant une plus grande résistance à la déformation (un module d'élasticité plus élevé) supportera une contrainte plus importante.
Par exemple, pour un tofu et un bloc de fer de même taille, si leur hauteur est réduite de 1 mm, il suffit de presser doucement le premier à la main, tandis que le second doit être aidé par un outil.
Le module d'élasticité des matériaux d'ingénierie courants est indiqué dans des tableaux. Par exemple, le module d'élasticité du béton C30 est de 30000MPa (1N/mm).2 = 1MPa), et le module d'élasticité de l'acier au carbone est de 206GPa.
Le module d'élasticité Ec du béton en compression et en traction doit être adopté conformément au tableau 4.1.5.
Le module de déformation en cisaillement Gc du béton peut être adopté à 40% de la valeur du module élastique correspondant.
Le coefficient de Poisson Vc du béton peut être fixé à 0,2.
Tableau4.15 Module d'élasticité du béton (×104N/mm2).
| Classe de résistance du béton | C15 | C20 | C25 | C30 | C35 | C40 | C45 | C50 | C55 | C60 | C65 | C70 | C75 | C80 |
| Ec | 2.20 | 2.55 | 2.80 | 3.00 | 3.15 | 3.25 | 3.35 | 3.45 | 3.55 | 3.60 | 3.65 | 3.70 | 3.75 | 3.80 |
Remarque :
1. Lorsque des données d'essai fiables sont disponibles, le module d'élasticité peut être déterminé sur la base des données mesurées ;
2. Lorsqu'une grande quantité d'adjuvants minéraux est ajoutée au béton, le module d'élasticité peut être déterminé sur la base des données réelles mesurées en fonction de l'âge spécifié.
Tableau 1.1-13 Module d'élasticité et coefficient de Poisson de matériaux couramment utilisés
| Objet | Module d'élasticité E/GPa | Module de cisaillement G/GPa | Rapport de Poisson μ | Objet | Module d'élasticité E/GPa | Module de cisaillement G/GPa | Téflon |
| Fonte grise | 118~126 | 44.3 | 0.3 | Zinc laminé | 82 | 31.4 | 0.27 |
| Fonte nodulaire | 173 | 0.3 | Plomb | 16 | 6.8 | 0.42 | |
| Acier au carbone, acier au nickel-chrome | 206 | 79.4 | 0.3 | Verre | 55 | 1.96 | 0.25 |
| Acier allié | Verre organique | 2.35-29.42 | |||||
| Acier moulé | 202 | 0.3 | Caoutchouc | 0.0078 | 0.47 | ||
| Cuivre pur laminé | 108 | 39.2 | 0.31-0.34 | Bakélite | 1.96-2.94 | 0.69-2.06 | 0.35-0.38 |
| Cuivre pur étiré à froid | 127 | 48.0 | Sandwich plastique phénolique | 3.92-8.83 | |||
| Bronze phosphoreux étain laminé | 113 | 41.2 | 0.32-0.35 | Celluloïd | 1.71-1.89 | 0.69-0.98 | 0.4 |
| Laiton étiré à froid | 89-97 | 34.3-36.3 | 0.32-0.42 | Nylon 1010 | 1.07 | ||
| Bronze au manganèse laminé | 108 | 39.2 | 0.35 | Chlorure de polyvinyle non plastifié | 3.14-3.92 | 0.35-0.38 | |
| Aluminium laminé | 68 | 25.5-26.5 | 0.32-0.36 | téflon | 1.14-1.42 | ||
| Fil d'aluminium tréfilé | 69 | Polyéthylène basse pression | 0.54-0.75 | ||||
| Aluminium moulé bronze | 103 | 41.1 | 0.3 | Polyéthylène haute pression | 0.147-0.245 | ||
| Bronze étain coulé | 103 | 0.3 | béton | 13.73~39.2 | |||
| Alliage de duralumin | 70 | 26.5 | 0.3 | 4.9-15.69 | 0.1-0.18 |
En effet, lorsque les contraintes internes ne peuvent être mesurées directement, elles peuvent être calculées en mesurant la déformation et en la multipliant par le module d'élasticité du matériau.