Dans cet article, nous explorons les concepts fascinants de résistance et de rigidité dans l'ingénierie. Vous apprendrez comment ces principes assurent la sécurité et la durabilité des objets du quotidien, des ponts aux écrans de smartphones. Rejoignez-nous pour découvrir les secrets des merveilles de l'ingénierie !
Pour garantir les performances et la fiabilité optimales d'un système ou d'une structure mécanique, chaque composant doit remplir sa fonction de manière efficace et efficiente. L'objectif premier de la conception de la sécurité des composants techniques est de garantir que tous les éléments possèdent une résistance, une rigidité et une stabilité adéquates, assurant ainsi l'intégrité globale et la longévité du système.
La stabilité est un concept fondamental en ingénierie, qui fait référence à la capacité d'un composant à maintenir ou à retrouver son état d'équilibre initial lorsqu'il est soumis à des forces extérieures. Ce principe est essentiel dans divers scénarios, tels que :
Ces exemples illustrent l'importance de la stabilité pour prévenir les défaillances catastrophiques et garantir la sécurité de fonctionnement des systèmes et structures mécaniques.
Dans cette discussion, je me concentrerai sur l'élucidation de ma compréhension globale de deux principes d'ingénierie tout aussi cruciaux : la rigidité et la résistance. Ces concepts, ainsi que la stabilité, forment la triade des considérations fondamentales dans la conception de la sécurité des composants, chacun jouant un rôle vital dans la détermination de la performance globale, de la durabilité et de la sécurité des systèmes techniques.
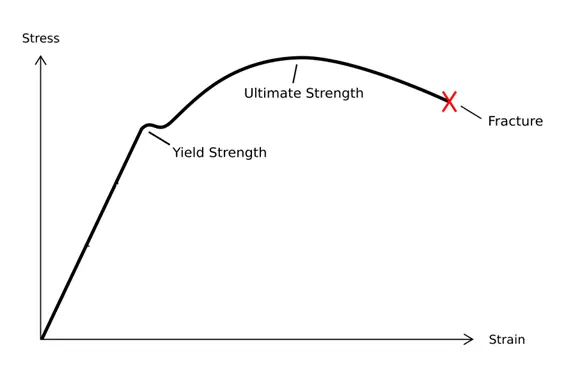
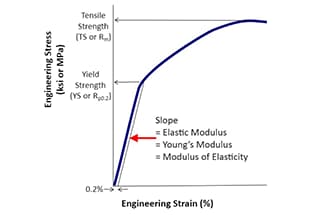
Définition : La résistance est la capacité des matériaux, des composants ou des structures à supporter des charges ou des forces appliquées sans défaillance, déformation excessive ou dommage. Il s'agit d'une propriété fondamentale de la science et de l'ingénierie des matériaux qui détermine la capacité d'un matériau à résister à une contrainte mécanique.
La force englobe différents aspects, notamment
Par exemple, dans le domaine de la fabrication métallique, il est essentiel de comprendre la résistance des matériaux pour concevoir des composants capables de supporter des charges opérationnelles. Une poutre en acier dans un bâtiment doit avoir une résistance suffisante pour supporter le poids de la structure et les charges supplémentaires sans se plier ou se rompre.
La force est influencée par divers facteurs, notamment
L'unité de mesure de la résistance est généralement exprimée en mégapascals (MPa) ou en livres par pouce carré (psi) en unités impériales. Par exemple, l'acier doux a une résistance à la traction d'environ 400-550 MPa, tandis que les aciers alliés à haute résistance peuvent dépasser 1000 MPa.
Dans les domaines de la fabrication et de l'ingénierie, les calculs et les essais de résistance sont essentiels pour.. :
Des techniques avancées telles que l'analyse par éléments finis (FEA) et les essais destructifs sont souvent utilisées pour évaluer et valider la résistance des matériaux et des composants dans des applications d'ingénierie complexes.
Fracture fragile : Mode de défaillance soudain et catastrophique caractérisé par une propagation rapide des fissures avec une déformation plastique minimale. Ce type de défaillance se produit sans avertissement et se traduit généralement par une surface de rupture propre et plane.
Par exemple :
Rendement plastique : Mode de défaillance dans lequel le matériau subit une déformation plastique importante, entraînant un changement de forme permanent et une perte d'intégrité structurelle. Ce type de défaillance est généralement plus progressif et observable que la rupture fragile.
Par exemple :
Il est important de noter que le mode de défaillance d'un matériau dépend de plusieurs facteurs, notamment les propriétés du matériau, les conditions de chargement, la température et les facteurs environnementaux. Certains matériaux peuvent présenter une transition entre un comportement ductile et un comportement fragile dans certaines conditions, telles que des températures basses ou des taux de déformation élevés.
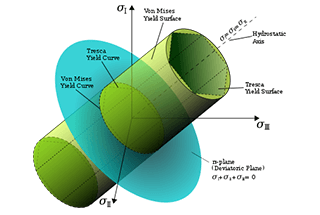
1. Théorie de la contrainte de traction maximale :
Lorsque la contrainte de traction maximale σ1 en un point de l'élément atteint la contrainte ultime σb dans des conditions de contrainte unidirectionnelle, le matériau subit une rupture fragile. Ainsi, les critères de rupture fragile des composants avec des points critiques dans des conditions de contraintes complexes sont : σ1 = σb.
Par conséquent, les conditions de résistance établies par le premier théorie de la résistance sont : σ1 ≤ σb.
2. Théorie de la déformation maximale en traction :
Lorsque la déformation de traction maximale ε1 atteint la valeur limite εu dans des conditions de contrainte unidirectionnelle, le matériau se rompt en raison d'une rupture fragile. Ceci peut être exprimé par ε1 = εu.
À partir de la loi de Hooke généralisée, nous pouvons calculer ε1 comme suit : ε1 = [σ1 - u(σ2 + σ3)] / E, donc σ1 - u(σ2 + σ3) = σb.
Les conditions de résistance établies par la deuxième théorie de la résistance sont : σ1 - u(σ2 + σ3) ≤ σb.
3. Théorie de la contrainte de cisaillement maximale :
Lorsque la contrainte de cisaillement maximale τMax atteint la contrainte de cisaillement ultime τ0 dans des conditions de contrainte unidirectionnelle, le matériau se rompt par cisaillement. Ceci peut être exprimé par τMax = τ0.
La formule de la contrainte de cisaillement sur une section inclinée pendant une tension axiale est τ0 = σs/2 (σs étant la contrainte normale sur la section transversale). La formule pour τMax est (σ1 - σ3)/2. Ainsi, la condition d'endommagement peut être réécrite comme σ1 - σ3 = σs.
La condition de résistance établie par la troisième théorie de la résistance est : σ1 - σ3 ≤ σs.
4. Théorie de l'énergie spécifique du changement de forme :
Lorsque le rapport de changement de forme en un point de l'élément atteint la valeur limite dans des conditions de contrainte unidirectionnelle, le matériau se rompt sous l'effet de la déformation.
La condition de résistance établie par la quatrième théorie de la résistance est la suivante :
√(σ1^2 + σ2^2 + σ3^2 - σ1σ2 - σ2σ3 - σ3σ1) < σs.
Définition : La rigidité désigne la capacité d'un matériau, d'un composant ou d'une structure à résister à une déformation ou à un déplacement élastique lorsqu'il est soumis à une force extérieure. Elle quantifie la mesure dans laquelle un système peut conserver sa forme et ses dimensions dans des limites admissibles sous l'effet de charges appliquées.
La rigidité est un paramètre fondamental en ingénierie qui caractérise la relation entre la force et la déformation dans un matériau ou une structure. Elle est définie comme le rapport entre la force appliquée et le déplacement résultant, indiquant la quantité de force nécessaire pour produire une unité de déformation. En termes mathématiques, la rigidité (k) s'exprime comme suit :
k = F / δ
Où ?
L'unité de rigidité est généralement la force par unité de longueur, telle que N/m (Newtons par mètre) dans le système SI ou lbf/in (livres-force par pouce) dans le système impérial.
En termes pratiques, la rigidité peut être conceptualisée en utilisant l'analogie d'un ressort. La constante du ressort, qui représente la rigidité d'un ressort, est définie comme le rapport entre la force de traction ou de compression appliquée et l'allongement ou la compression qui en résulte. Cette relation est décrite par la loi de Hooke pour les systèmes élastiques linéaires.
La compréhension et le contrôle de la rigidité sont essentiels dans diverses applications techniques, notamment :
Les ingénieurs doivent trouver un équilibre entre les exigences de rigidité et d'autres considérations de conception telles que la résistance, le poids, le coût et la fabricabilité afin de créer des solutions optimales pour des applications spécifiques.
Lorsque la charge appliquée est constante, on parle de rigidité statique.
Lorsque la charge alterne, on parle de rigidité dynamique.
La rigidité statique englobe la rigidité structurelle et la rigidité de contact.
La rigidité structurelle fait référence à la rigidité de l'élément lui-même et comprend la rigidité en flexion et la rigidité en torsion.
1. Rigidité en flexion : calculée selon la formule suivante :
K=P/δ
Où
2. La rigidité à la torsion est calculée selon la formule suivante :
Km=ML/θ
Où M - couple appliqué (n - m) ;
L - distance entre la position d'action du couple et l'extrémité fixe (m) ;
θ-- Angle de torsion (°)
L'explication ci-dessus de la résistance et de la rigidité montre que la résistance est axée sur la rupture sous l'effet d'une force extérieure et qu'elle est classée en deux catégories : la rupture plastique et la rupture fragile, qui est liée à la courbe contrainte-déformation lors d'un essai de traction. En revanche, la rigidité concerne la relation entre la déformation et la force.
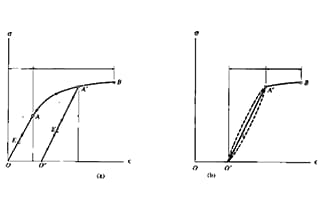
Comme le montre la fig.
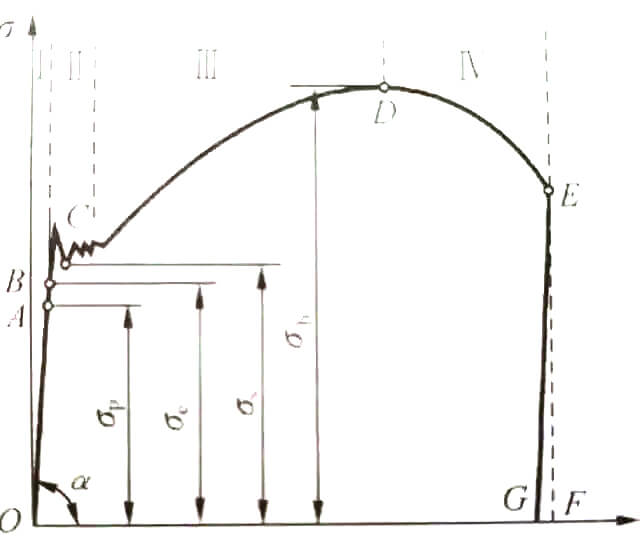
La courbe de la figure peut être divisée en quatre étapes :
1. Phase de déformation élastique ;
2. Stade de rendement ;
3. Phase de renforcement ;
4. Stade de collet local.
La rigidité est définie comme la résistance à la déformation élastique, qui se produit dans la phase initiale, et est régie par la loi de Hooke dans des conditions élastiques.
Calcul de la rigidité en flexion et de la rigidité en torsion sous charges statiques est similaire à la loi de Hooke, ce qui suggère que la rigidité n'est mesurée que pendant la phase de déformation élastique.
Au stade suivant, lorsque la déformation plastique se produit pendant l'essai de traction, la déformation résiduelle ne disparaît pas. Sur la courbe contrainte-déformation, bien que la contrainte reste pratiquement inchangée, la déformation augmente considérablement. À ce stade, la contrainte atteint la limite d'élasticité et le matériau entre dans la phase de rupture plastique. À mesure que la contrainte continue d'augmenter, la déformation augmente également jusqu'à ce qu'elle atteigne la limite de résistance.
Par conséquent, la mesure de la résistance intervient après que le matériau a subi une déformation élastique et avant qu'il n'atteigne la limite de résistance.
En conclusion, la rigidité et la résistance sont toutes deux évaluées pendant la phase de rupture des pièces, la rigidité étant mesurée par la contrainte et la résistance par la déformation.
En termes d'ordre dans le processus de déformation, la rigidité intervient au premier stade, tandis que la résistance intervient au dernier stade.
Par conséquent, lors de l'évaluation des conditions de défaillance des pièces, tant que les exigences de rigidité sont satisfaites, la pièce devrait être capable de résister à une contrainte suffisante pendant la phase de déformation élastique, qui à son tour devrait satisfaire aux exigences de résistance.
Cette relation se reflète dans diverses conceptions, telles que l'arbre d'un équipement mécanique. Généralement, la taille de l'arbre est déterminée en fonction des conditions de résistance, puis sa rigidité est vérifiée en fonction des conditions de rigidité.
Par conséquent, les exigences en matière de rigidité des arbres des machines de précision sont très élevées, et la conception de la taille de la section transversale est souvent contrôlée par les conditions de rigidité.
En tant que fondateur de MachineMFG, j'ai consacré plus d'une décennie de ma carrière à l'industrie métallurgique. Ma vaste expérience m'a permis de devenir un expert dans les domaines de la fabrication de tôles, de l'usinage, de l'ingénierie mécanique et des machines-outils pour les métaux. Je suis constamment en train de réfléchir, de lire et d'écrire sur ces sujets, m'efforçant constamment de rester à la pointe de mon domaine. Laissez mes connaissances et mon expertise être un atout pour votre entreprise.
FR 
EN 
AR 
DE 
ES 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO