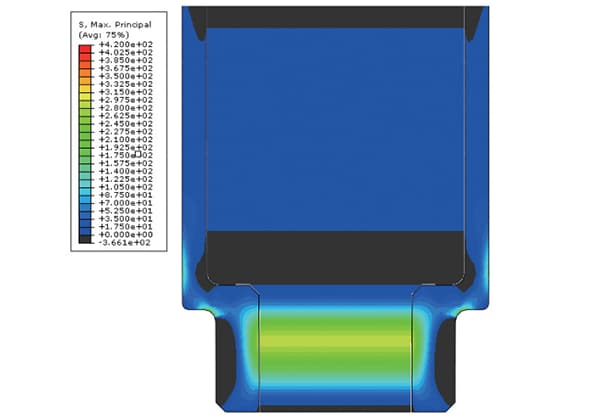
Imaginez que vous sachiez exactement quelle contrainte vos composants métalliques peuvent supporter sans avoir à les découper. La mesure des contraintes résiduelles par rayons X offre cette possibilité en utilisant des méthodes d'essai non destructives. Cet article explique comment les techniques de diffraction des rayons X mesurent avec précision les contraintes internes, améliorant ainsi la fiabilité et la longévité des produits. Découvrez comment différentes méthodes, telles que les techniques sin²ψ et cosα, fournissent des données précises sur les contraintes, garantissant ainsi la conformité de votre métallurgie aux normes les plus strictes. Plongez dans ces techniques de mesure avancées pour comprendre leurs principes, leurs applications et leurs avantages pour l'ingénierie industrielle.
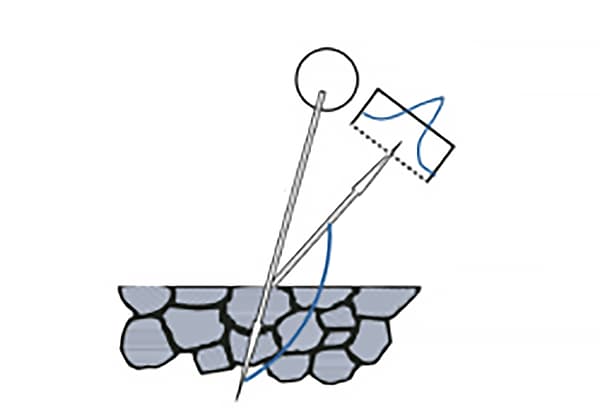
Les contraintes résiduelles sont un type de contrainte interne appelé ainsi dans le domaine de l'ingénierie. La distribution des contraintes résiduelles dans une pièce est souvent inégale, ce qui peut avoir un impact significatif sur sa résistance statique, sa résistance à la fatigue, sa stabilité de forme et sa résistance à la corrosion. Il est donc essentiel de mesurer les contraintes résiduelles.
Il existe deux méthodes principales pour mesurer contrainte résiduelleLes méthodes de contrôle sont les suivantes : le contrôle destructif et le contrôle non destructif. La méthode de contrôle destructif consiste à enlever une partie de la pièce et à calculer la valeur de l'échantillon. contrainte résiduelle sur la base de la déformation et du déplacement correspondants. Les méthodes d'essai destructif les plus courantes sont les suivantes forage et la méthode du noyau annulaire.
La méthode de contrôle non destructif consiste à établir une relation entre la contrainte résiduelle et une grandeur physique susceptible de provoquer un changement dans le matériau (comme l'espacement des plans cristallins, la vitesse de propagation des ondes ultrasoniques ou la perméabilité magnétique) afin de calculer la contrainte résiduelle. Les méthodes de contrôle non destructif comprennent la diffraction des rayons X, la diffraction des neutrons, les méthodes magnétiques et les méthodes ultrasoniques.
La diffraction des rayons X est la méthode la plus utilisée pour mesurer les contraintes résiduelles, en raison de la maturité de ses principes et de ses méthodes bien établies, ainsi que de la disponibilité d'équipements d'essai de plus en plus sophistiqués, y compris des instruments de laboratoire, des instruments portables pour les mesures sur le terrain et des appareils spécialisés pour des circonstances particulières.
La méthode de diffraction des rayons X pour mesurer les contraintes résiduelles a été proposée pour la première fois par le chercheur russe Akchenov en 1929 et a permis d'assimiler la déformation macroscopique à la déformation du réseau. En 1961, l'Allemand Macherauch a développé la méthode de mesure des contraintes résiduelles.2ψ basée sur l'idée d'Akchenov, faisant de la mesure des contraintes résiduelles par diffraction des rayons X une technologie fiable et largement utilisée.
Au cours des 60 dernières années, la diffraction des rayons X s'est développée en plusieurs méthodes de mesure différentes, dont la sin.2La méthode ψ et la méthode cosα sont les deux principales méthodes actuellement utilisées.
Pour maîtriser la technologie de la diffraction des rayons X pour mesurer les contraintes résiduelles, il est important de comprendre ses différentes méthodes.
(1) Les méthodes de mesure des contraintes résiduelles par diffraction des rayons X peuvent être classées en deux catégories principales : la méthode sin2ψ et la méthode cosα.
(2) Le péché2La méthode ψ peut également être classée, en fonction de la méthode de calcul des contraintes résiduelles, en méthode 2θ, méthode de la valeur d et méthode de la déformation.
(3) Sur la base de la relation géométrique entre ψ et 2θ, le sin2La méthode ψ peut être divisée en deux types : la méthode de co-inclinaison et la méthode de roulement.
(4) La méthode de mesure peut également être différenciée en fonction du mode de balayage du tube à rayons X et du contre-tube, en méthode ψ0 fixe et méthode ψ fixe.
(5) La méthode du rouleau comprend trois sous-catégories : la méthode du rouleau standard, la méthode du rouleau modifié et la méthode de fixation du rouleau ψ.
(6) La méthode de mesure ψ positive et négative est utilisée pour déterminer la contrainte de cisaillement τφ.
(7) La diffraction des rayons X est généralement utilisée pour mesurer la contrainte dans une direction spécifique en un point particulier, mais il existe également des méthodes pour mesurer la contrainte principale en un point.
(8) La méthode de l'oscillation peut être divisée en plusieurs sous-catégories : la méthode de l'oscillation ψ0, la méthode de l'oscillation ψ, la méthode de l'oscillation de l'anneau de Debye, la méthode de l'oscillation de l'angle φ et la méthode de la translation réciproque X/Y.
(9) En termes de géométrie de diffraction, il existe trois approches : la méthode de focalisation, la méthode de quasi-focalisation et la méthode des faisceaux parallèles.
La contrainte est déterminée par la déformation. Dans le cas des matériaux polycristallins, la contrainte résiduelle est estimée par le résultat statistique de la déformation du réseau dans la région concernée.
Ainsi, la contrainte résiduelle peut être déterminée en mesurant la déformation du réseau par la technique de diffraction des rayons X.
La contrainte résiduelle du matériau reflète la macro-déformation.
La macro-déformation est équivalente à la déformation du réseau.
La déformation du réseau représente la variation relative de l'espacement entre les plans cristallins, qui peut être calculée à l'aide d'un dispositif de diffraction basé sur la loi de Bragg.
Ce document résume la méthode de diffraction des rayons X pour mesurer les contraintes résiduelles.
Lorsqu'un polycristal est exposé à un faisceau de rayons X d'une longueur d'onde spécifique (λ), l'intensité maximale des rayons X réfléchis (c'est-à-dire le pic de diffraction) est observée à un angle de diffraction spécifique (2θ), comme l'illustre la figure 1. Ce phénomène est connu sous le nom de diffraction des rayons X.
La relation entre la longueur d'onde des rayons X (λ), l'espacement des plans cristallins (d) et l'angle de Bragg (θ) est décrite par l'équation suivante (1).

Dans l'analyse des contraintes résiduelles par diffraction des rayons X, le matériau cible approprié pour le tube à rayons X est sélectionné pour déterminer la longueur d'onde appropriée (λ). L'angle de diffraction (2θ) est ensuite mesuré à l'aide d'un appareil de diffraction. Sur la base de cette mesure, l'espacement entre les plans cristallins (d) du plan cristallin concerné peut être calculé.

Fig. 1 Géométrie de diffraction des rayons X
Selon la loi de réflexion de l'optique, la normale du plan cristallin impliqué dans la diffraction doit se situer sur la bissectrice entre le rayon entrant et le rayon réfléchi, comme l'illustre la figure 2.
L'angle entre la normale du plan du cristal de diffraction et la normale de la surface de l'échantillon est appelé angle d'azimut de la normale du plan du cristal de diffraction, qui est généralement représenté par ψ.

Fig. 2 Schéma de la diffraction des rayons X Plan cristallin Azimut ψ
La loi de Bragg permet de déterminer l'espacement (dψ) des plans cristallins dans une orientation donnée (ψ).
Si l'on connaît l'espacement (d0) des plans cristallins à l'état libre de contraintes, on peut calculer la déformation du réseau (εψ) dans l'orientation désignée.
S1, S2 et S3 sont les axes de la surface de l'échantillon et S1 est défini par le chercheur.
La figure 3 illustre le système de coordonnées utilisé pour mesurer les contraintes résiduelles par diffraction des rayons X.

Fig. 3 Système de coordonnées pour la mesure des contraintes par diffraction des rayons X
Selon la loi de Hooke généralisée, les déformations de ces plans cristallins sont influencées par le tenseur des contraintes au point O et sont étroitement liées au sinus et au cosinus de φ et ψ, au module d'Young du matériau et au coefficient de Poisson.
Il est donc possible de déterminer la contrainte tridimensionnelle au point O, y compris la contrainte (σφ).
L'expression de la déformation dans la direction OP peut être dérivée de la théorie de l'élasticité.
Pour la plupart des matériaux et des composants, la profondeur de pénétration des rayons X n'est que de quelques microns à quelques dizaines de microns, et il est donc communément admis que σ33=0.
Par conséquent, la déformation dans la direction OP est représentée par l'équation (2).


Le péché2La formule de la méthode ψ est dérivée de la loi de Bragg et de la théorie élastique.
Les objets considérés dans la théorie de l'élasticité sont supposés être des milieux homogènes, continus et isotropes.
Toutefois, cette hypothèse n'est valable que pour les matériaux polycristallins. matériaux métalliques si la granulométrie est fine et qu'il n'y a pas de texture.
La figure 4 montre la courbe de relation fonctionnelle de εn et le péché2ψ pour les matériaux isotropes, les matériaux avec gradient de contrainte ou gradient de composition, les matériaux avec contrainte de cisaillement et les matériaux anisotropes avec texture.

Comme le montre la figure 4c), si la contrainte de cisaillement τ13≠ 0, τ23≠0 et sin2ψ ont une bifurcation ± ψ, σφ et τφ peut être obtenue en utilisant les données de déformation mesurées ε﹢ψ et ε-ψ sur une série d'angles ± ψ, comme indiqué dans les formules (4) et (5).

Il est important de noter que le péché2ψ illustrée à la figure 4c) n'est pas susceptible de présenter une bifurcation ±ψ.
En effet, les rayons X utilisés pour la diffraction ont une profondeur de pénétration limitée dans le matériau testé, généralement de quelques microns à quelques dizaines de microns.
Par conséquent, les composantes de la contrainte perpendiculaires à la surface du matériau peuvent être considérées comme nulles.
Ce n'est que lorsque le plan de contrainte principale s'écarte de la surface de l'échantillon dans les conditions d'un usinage spécial (tel que le meulage puissant et à grande quantité de coupe) que τ13≠0 et τ23≠0 se produisent.
La bifurcation ±ψ n'est pas fréquente et la courbe d'ajustement n'a souvent pas l'attribut d'ellipse. Cela est dû en grande partie à l'erreur systématique dans le mécanisme ±ψ du goniomètre. Il n'est donc pas nécessaire d'insister outre mesure sur l'importance de l'ajustement à l'ellipse.
En conclusion, le processus pratique et réalisable de détermination des contraintes résiduelles par diffraction des rayons X consiste à sélectionner quelques angles ψ (ou plusieurs paires d'angles ±ψ) et à mesurer l'angle de diffraction correspondant (2θφψ), puis à le calculer.
Les chercheurs ont développé diverses méthodes pour organiser la relation géométrique spatiale entre le plan ψ et le plan 2θ, déterminer la courbe de diffraction et effectuer des calculs.
L'angle de diffraction 2θφψ est mesuré par le dispositif de diffraction des rayons X, et l'espacement correspondant entre les plans cristallins est calculé comme suit : dφψ selon la loi de Bragg, alors la déformation du réseau εφψ peut être exprimée par l'espacement entre les plans de cristal, comme le montre la formule (6).

La contrainte réelle est directement substituée dans les équations (3), (4) et (5) pour calculer la contrainte, qui est l'expression de la méthode de la contrainte réelle.
La méthode de la contrainte réelle est adoptée, et les valeurs exactes de d0 et θ0 ne sont pas nécessaires.
Dans la plupart des cas, la méthode de la contrainte réelle présente des avantages significatifs.
Des équations approximatives peuvent également être utilisées pour calculer la déformation, comme le montrent les équations (7) et (8).

La formule de calcul de la méthode 2θ est présentée dans l'équation (9).

Où K est la constante de contrainte, et sa formule de calcul est présentée dans l'équation (10).

Où : ν est le coefficient de Poisson du matériau.
Pour certains matériaux, θ0 varie considérablement en fonction de la composition chimique, et les résultats seront très différents si l'on utilise la constante de contrainte.
La méthode de la contrainte réelle a été incluse dans la norme de l'Union européenne EN 15305-2008 Essais non destructifs - Méthode d'essai pour l'analyse des contraintes résiduelles par diffraction des rayons X et GB/T 7704-2017 Essais non destructifs - Méthode de mesure des contraintes par rayons X.
L'appareil de mesure des contraintes domestiques XL-640 utilise la méthode de la contrainte réelle comme méthode de calcul des contraintes par défaut, et la méthode 2θ peut être sélectionnée pour le calcul.
La méthode coplanaire est une méthode de mesure dans laquelle le plan 2θ coïncide avec le plan ψ (plan de direction des contraintes), comme le montre la figure 5.

Fig. 5 Diagramme géométrique de la même méthode d'inclinaison
Avec la même méthode d'inclinaison, l'angle d'incidence des rayons X ψ0 est dominant, tandis que l'angle ψ peut être calculé, comme le montrent les équations (11) et (12).

Dans l'essai de contrainte de la pièce réelle, lorsque le point d'essai est situé dans une rainure similaire peu profonde, l'espace d'essai du goniomètre est limité, de sorte que la même méthode d'inclinaison est plus appropriée.
La méthode du rouleau est une méthode de mesure dans laquelle le plan 2θ et le plan ψ (plan de direction des contraintes) sont perpendiculaires l'un à l'autre, comme le montre la figure 6.

Fig. 6 Schéma géométrique de la méthode du rouleau
La principale caractéristique de la méthode de Roll (méthode χ) est son faible facteur d'absorption du pic de diffraction, qui contribue à améliorer la précision des mesures.
Les gammes 2θ et ψ peuvent être entièrement étendues si nécessaire. Pour certains matériaux, les rayons diffractifs dont les pics sont peu élevés (tels que les pics inférieurs à 145°) peuvent être utilisés pour la mesure des contraintes.
Cependant, le plan 2θ et le plan ψ de cette méthode sont perpendiculaires l'un à l'autre, ce qui nécessite un espace tridimensionnel et rend difficile son application à la mesure d'espaces étroits.
L'instrument de mesure du stress d'une société étrangère utilise une méthode de Roll modifiée avec des détecteurs doubles, comme le montre la figure 7. Sa disposition géométrique est décrite dans la figure.

Fig. 7 Diagramme géométrique de la méthode du rouleau modifié
Dès janvier 1977, Li Jiabao, de l'Institut des métaux de l'Académie chinoise des sciences, a proposé cette méthode d'essai et cette formule de calcul, comme le montrent les équations (13) et (14).
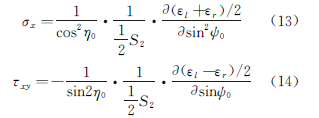
La méthode du rouleau peut être divisée en deux catégories : la méthode ψ0 fixe et la méthode ψ fixe.
La méthode ψ fixe est considérée comme supérieure à la méthode ψ0 fixe en raison de ses principes plus précis et de ses résultats efficaces dans la pratique.
En combinant ces deux méthodes, la méthode du rouleau fixe ψ, le facteur d'absorption peut être égal à 1.
Cela signifie que le pic de diffraction ne s'inclinera pas à l'arrière-plan, que la forme du pic restera symétrique et que la forme et l'intensité du pic resteront inchangées, même si l'angle ψ change, tant qu'il n'y a pas de texture.
Cette caractéristique améliore considérablement la précision des mesures, ce qui fait de la méthode du rouleau fixe ψ une technique de mesure idéale.
La méthode d'oscillation consiste à utiliser chaque angle ψ (ou angle ψ0) comme point central et à faire osciller le tube à rayons X et le détecteur vers la gauche et la droite selon un angle spécifique (±Δψ ou ±Δψ0).
Cette méthode augmente le nombre de grains qui participent à la diffraction, ce qui en fait une méthode efficace pour mesurer la contrainte dans les matériaux à gros grains.
D'autres méthodes d'oscillation, telles que la méthode de l'angle φ et la méthode de la translation X/Y, peuvent également être utilisées, et différentes méthodes d'oscillation peuvent même être combinées à des fins de test.
En 2012, la société japonaise PULSTEC a présenté un instrument de mesure du stress qui utilise pour la première fois la technologie des détecteurs bidimensionnels.
Cet instrument utilise un mode d'incidence unique et un détecteur bidimensionnel pour recueillir des informations sur la diffraction des rayons X, ce qui lui permet de collecter rapidement des données sur l'anneau de Debye au point d'essai.
Comme l'angle ψ formé par la normale à la face du cristal et la normale à la surface de l'échantillon ne se situe pas dans le même plan pour chaque point de l'anneau de Debye, le sin2La méthode ψ ne peut pas être utilisée pour calculer les contraintes. En revanche, la méthode de l'angle α, ou cosα, est utilisée (comme le montre la figure 8).
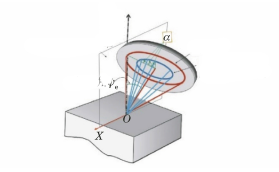
Fig. 8 Diagramme géométrique de la méthode cosα
Cette méthode d'essai est idéale pour mesurer les contraintes de surface dans les grandes structures en acier.
Cependant, elle présente des limites lorsqu'il s'agit de tester des matériaux à gros grains ou des matériaux texturés.
La méthode cosα est basée sur les principes de l'élasticité, comme le montrent les équations (15) et (16).

La figure 9 montre la plage maximale de l'angle ψ qui peut être acquise en utilisant un "détecteur complet à deux positions" (avec un angle d'incidence de 45°).
L'angle α se situe sur le plan de l'anneau de Debye, qui est l'angle central de chaque point de l'anneau de Debye.

Fig. 9 Emplacement des points de données de la méthode sin2ψ dans la courbe s
Les deux méthodes de mesure des contraintes résiduelles par diffraction des rayons X reposent sur le même principe mécanique.
Le tenseur de déformation peut être transformé en angle spatial, et l'angle α utilisé dans la méthode cosα peut être entièrement converti en angle ψ.
La méthode cosα est essentiellement une approximation de la méthode sin2Méthode ψ.
En règle générale, les tôles d'acier laminées à chaud sont considérées comme exemptes de texture. Cependant, certaines parties de la tôle d'acier peut présenter une texture due à différents facteurs.
Malgré cela, de nombreux utilisateurs choisissent encore d'utiliser la diffraction des rayons X pour mesurer les contraintes résiduelles dans de tels cas.
Par exemple, si l'on choisit une plaque d'acier laminée à chaud avec texture, les conditions d'essai et les résultats sont indiqués dans les tableaux 1 et 2. Le rapport d'essai pour la mesure de la contrainte résiduelle au point Z (0) par chaque instrument est présenté dans les figures 10 à 13.
Tableau 1 Paramètres d'essai pour la mesure de la contrainte résiduelle à chaud Acier laminé Plaque avec différents instruments de contrainte
| Type d'équipement | μ-X360S | PROTO LXRD | X-RAYBOT | XL-640 |
| méthode d'essai | cosα | péché2ψ | péché2ψ | péché2ψ |
| Tension/kV | 20 | 30 | 20 | 25 |
| Courant/mA | 1 | 25 | 1 | 6 |
| Point lumineux/mm | 1 | 1 | 1 | 1 |
| Gamme ψ/(°) | – | -35~35 | -40~40 | 0~45 |
| Méthode de calcul des déformations | – | Méthode de la valeur D | Méthode de contrainte | Méthode de contrainte |
| Méthode de détermination des pics | – | PersonneVII | Point médian | Méthode de corrélation croisée |
| Contrainte résiduelle/MPa | 78 | 213.6 | 144 | 113 |
Tableau 2 Contrainte résiduelle d'une tôle d'acier laminée à chaud mesurée par différents instruments de mesure de la contrainte
| Point de test | μ-X360S | PROTO LXRD | X-RAYBOT | XL-640 |
| Z(5) | 29,47 | 122 | 107 | 77 |
| Z(4) | 37,52 | 135 | 112 | 70 |
| Z(3) | 74,70 | 104 | 95 | 67 |
| Z(2) | 38,28 | 153 | 99 | 134 |
| Z(1) | 37,64 | 166 | 122 | 101 |
| Z(0) | 64,78 | 144 | 213 | 113 |
| Z(-1) | 72,71 | 138 | 97 | 139 |
| Z(-2) | 62,52 | 134 | 83 | 145 |
| Z(-3) | 75,70 | 120 | 93 | 153 |
| Z(-4) | 63,56 | 114 | 80 | 148 |
| Z(-5) | 79,27 | 94 | 93 | 152 |

Fig. 10. Anneau de Debye au point Z (0) mesuré avec un appareil de mesure de la contrainte de type μ-X360S.

Fig. 11 2θ-sin2Courbe ψ de Z (0) mesurée par l'appareil de mesure de la contrainte PROTO LXRD

Fig. 12 2θ-sin2Courbe ψ du point de mesure Z (0) avec l'appareil de mesure des contraintes X-RAYBOT

Fig. 13 ε-sin2Courbe ψ de Z (0) mesurée avec l'appareil de mesure de la contrainte XL-640
La contrainte résiduelle mesurée par la méthode c est plus faible que celle mesurée par la méthode s.
Pour le point d'essai Z (0), on utilise l'appareil de mesure de la contrainte. Selon le principe de l'espacement égal des sin2ψ, 8 angles ψ sont sélectionnés dans la plage de 0 °~45 °.
Les résultats sont présentés dans les Fig. 14-15. On constate que le sin2La courbe ψ du matériau présente un type de "choc" dû à la texture.
L'ordonnée du sin2La courbe ψ de la figure 13 est la déformation ε. Après avoir changé l'ordonnée en 2θ, effectuez un ajustement linéaire. Les résultats sont présentés à la figure 14.
La pente M de la ligne d'ajustement est de -0,355 et la contrainte résiduelle σ est de 113MPa.

Fig. 14 Résultats de l'ajustement de 2θ-sin2Courbe ψ mesurée par l'appareil de mesure de contrainte XL-640 au point Z (0)
La plage ψ sélectionnée par le mesureur de contrainte μ-X360S est équivalente aux deux premières valeurs 2θ du blindage, puis l'ajustement de la ligne droite est effectué. Les résultats sont présentés à la figure 15.

Fig. 15 Résultats de l'ajustement de 2θ-sin2Courbe ψ de Z (0) mesurée par l'instrument de mesure des contraintes de type μ-X360S
Utilisez l'appareil de mesure de la contrainte PROTO LXRD pour tester la plage ψ sélectionnée, protégez les trois dernières valeurs 2θ de la figure 14, puis effectuez un ajustement linéaire. Les résultats sont présentés à la figure 16.

Fig. 16 Résultats de l'ajustement de 2θ-sin2Courbe ψ mesurée par l'appareil de mesure de la contrainte PROTO LXRD au point Z (0)
La figure 12 montre que la valeur maximale du sin2La valeur ψ du point Z (0) est de 0,4 en utilisant l'appareil de mesure de la contrainte X-RAYBOT.
En fonction de la plage ψ sélectionnée, écranter les deux dernières valeurs 2θ de la figure 14, puis procéder à un ajustement linéaire. Les résultats sont présentés à la figure 17.

Fig. 17 Résultats de l'ajustement de 2θ-sin2Courbe ψ de Z (0) mesurée par le testeur de contraintes X-RAYBOT
En raison de la texture du matériau, son sin2La courbe ψ est oscillante.
La plage d'angle ψ sélectionnée est différente, ce qui entraîne des différences dans la pente et les valeurs de contrainte résiduelle obtenues à partir de la ligne d'ajustement.
Pour les matériaux dont la texture est inconnue et le grain grossier, il n'est pas conseillé de choisir une plage ψ étroite et un petit nombre de stations ψ pour la mesure des contraintes résiduelles, car cela peut entraîner des erreurs de mesure significatives.
L'ajustement linéaire peut ne pas être approprié pour les matériaux présentant une surface texturée.2les courbes ψ qui sont oscillantes.
Pendant le processus de mesure, l'ajustement linéaire est souvent utilisé pour atténuer les fluctuations causées par les vibrations et les erreurs de mesure.
Il n'est peut-être pas possible d'atteindre un angle ψ de 45°, car cela pourrait être influencé par la profondeur de pénétration. Un angle plus grand est plus susceptible de produire des résultats plus précis, à condition que la profondeur de pénétration puisse être ignorée.
Pour les matériaux à gros grains ou à texture grossière, la plage d'angles ψ doit être étendue autant que possible afin d'éliminer les effets de l'angle non linéaire ε-sin2ψ. Ceci peut être réalisé en mesurant les deux angles ±ψ.
La précision des droites ajustées peut être améliorée en utilisant la méthode des moindres carrés pour l'ajustement de la régression et en augmentant à la fois la plage ψ et le nombre de stations ψ. Cela permettra d'obtenir des valeurs de test plus fiables.
La précision de la mesure peut également être améliorée en augmentant la zone d'exposition aux rayons X ou en augmentant le nombre de grains de diffraction participant à la méthode de basculement.
(1) Le péché2La méthode ψ peut être utilisée pour déterminer la contrainte résiduelle avec une meilleure précision en augmentant la plage de ψ et en sélectionnant davantage de stations ψ. Toutefois, cette méthode présente des limites car elle implique une exposition unique, ce qui peut entraîner des erreurs de mesure importantes si la plage de ψ n'est pas suffisante.
(2) Dans les méthodes de mesure qui utilisent le sin2ψ, la méthode du rouleau est supérieure à la méthode de l'inclinaison. Il est recommandé d'utiliser la méthode du rouleau lorsque les conditions d'espace au point de mesure le permettent. Pour mesurer les contraintes résiduelles dans les rainures de certains composants, la méthode de co-inclinaison est couramment utilisée.
(3) La méthode de la déformation réelle est une méthode privilégiée pour le calcul des contraintes résiduelles.
(4) La méthode sin2ψ est considérée comme une méthode standard à cette fin. Pour obtenir les résultats les plus précis, l'angle ψ doit être fixé à l'aide de la méthode sin2La méthode de bissection de la valeur ψ et le plus grand nombre possible d'angles ψ doivent être mesurés.