Panduan Pakar untuk Menghitung Tegangan Geser Lentur dan Kekuatan Balok

Terdapat momen lentur dan gaya geser pada penampang balok yang dikenai gaya melintang, yang menghasilkan tegangan normal dan tegangan geser pada penampang. Tegangan geser lentur dari beberapa penampang balok yang umum akan dibahas selanjutnya.

Bagian persegi panjang

Segmen kecil dengan panjang dx dipotong dari balok di bawah tekukan gaya transversal. Balok tidak memiliki beban dan gaya geser pada kedua sisi segmen sama besar tetapi berlawanan arah. Momen lentur pada bagian kanan lebih besar dari pada bagian kiri, sehingga menghasilkan tegangan normal yang berbeda pada kedua bagian tersebut.

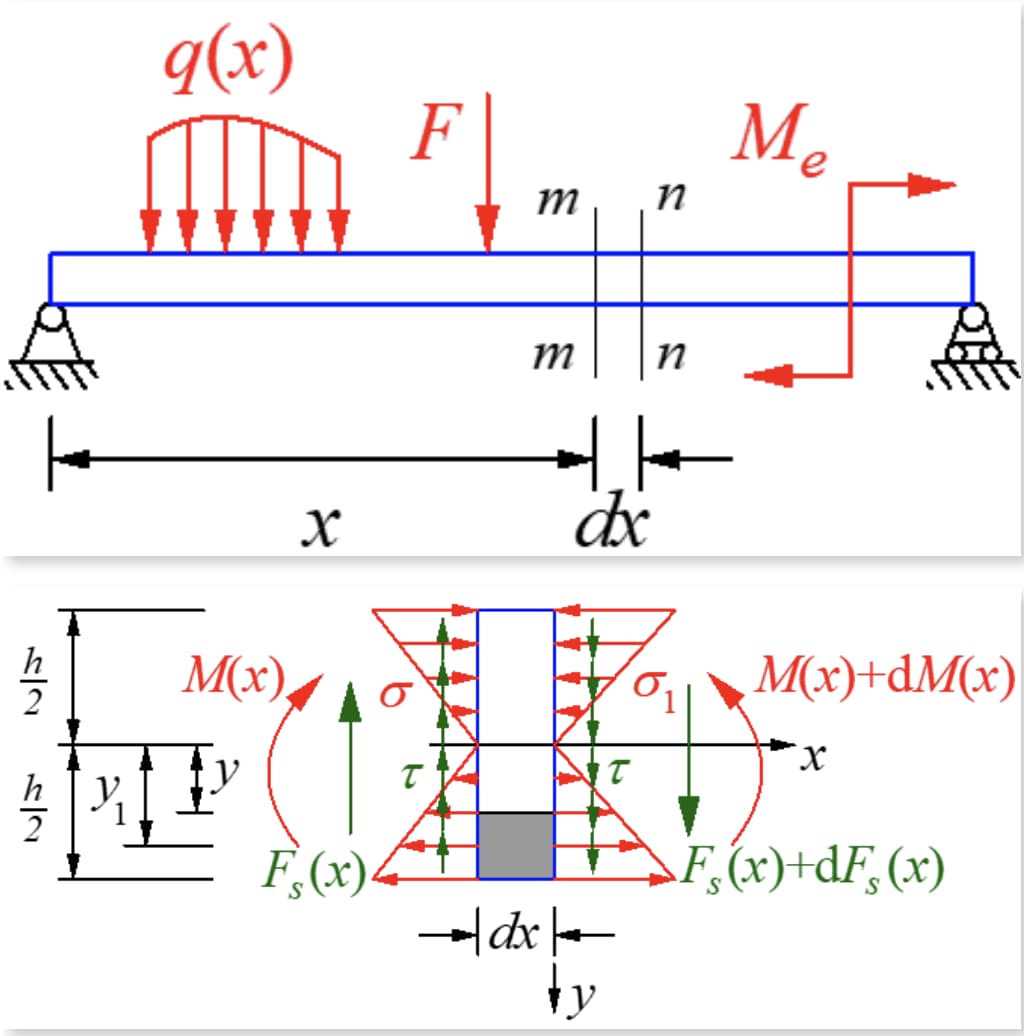
Untuk penampang persegi panjang yang sempit, tegangan geser bersinggungan dengan batas pada kedua sisi balok karena tidak adanya tegangan geser pada sisi tersebut. Ini berarti bahwa, karena balok ditekuk secara simetris dan sejajar dengan batas, tegangan geser pada sumbu y dari sumbu simetri harus berada pada arah y dan sedikit berubah di sepanjang arah lebar.

Oleh karena itu, asumsi berikut ini dibuat tentang hukum distribusi tegangan geser pada penampang:

• Arah tegangan geser pada setiap titik pada penampang sejajar dengan gaya geser;
• Tegangan geser didistribusikan secara merata di sepanjang lebar penampang, yaitu tegangan geser pada setiap titik pada garis horizontal yang sejajar dengan sumbu netral adalah sama.

Apabila rasio tinggi terhadap lebar penampang lebih besar dari 2, solusi berdasarkan asumsi di atas cukup akurat dibandingkan dengan solusi yang tepat dari teori elastis.

Menurut teorema timbal balik tegangan geser, harus ada tegangan geser yang sama dengan ukuran penampang melintang pada penampang memanjang yang tegak lurus dengan penampang melintang. Potong segmen mikro di sepanjang bidang longitudinal dengan sumbu netral momen menjauhi y, dan ambil elemen mikro di sisi bawah bidang longitudinal. Gaya-gaya seperti yang ditunjukkan pada gambar di bawah ini.

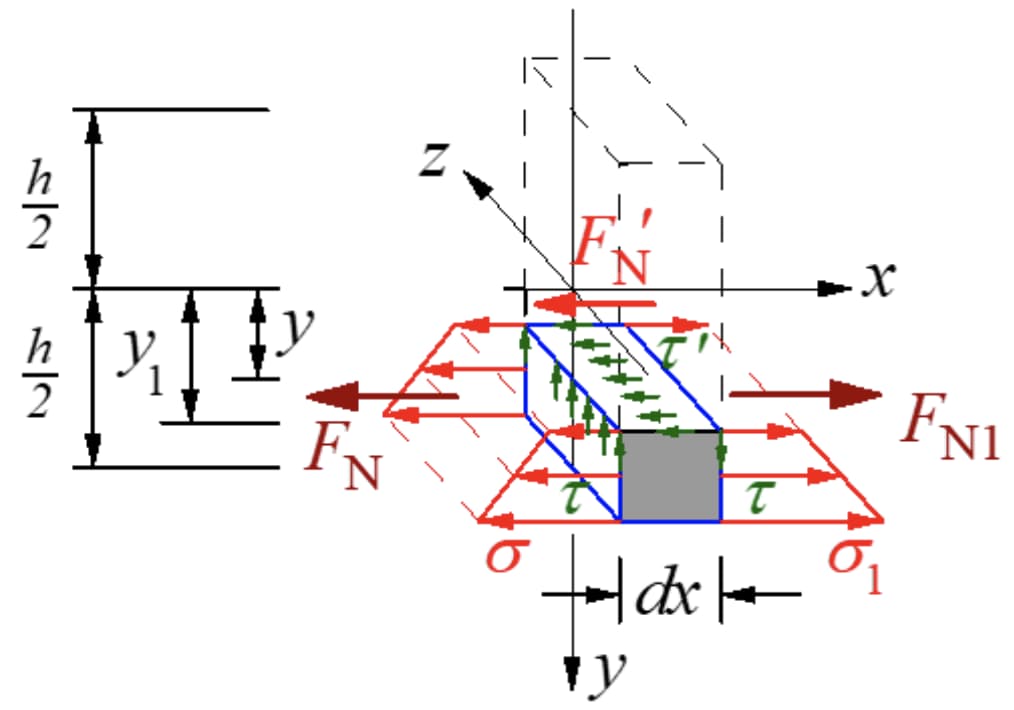
Gaya resultan dari tekanan normal pada bagian kiri adalah:

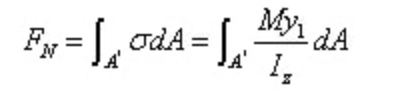
Gaya resultan dari tekanan normal pada bagian kanan adalah:: Gaya resultan dari tekanan normal pada bagian kanan adalah

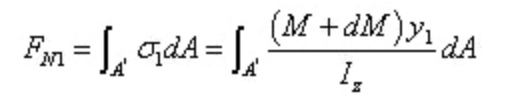
Jelaslah bahwa kedua resultan tersebut memiliki ukuran yang berbeda. Suatu gaya di sepanjang arah aksial harus ada pada penampang longitudinal untuk menjaga keseimbangan segmen mikro. Gaya ini adalah hasil dari tegangan geser, yang mengonfirmasikan adanya tegangan geser pada penampang memanjang.

Karena dx adalah jumlah yang kecil, biarkan tegangan geser pada bidang longitudinal terdistribusi secara merata::.

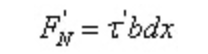
Menurut kondisi kesetimbangan: Menurut kondisi kesetimbangan

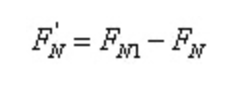
Ya,

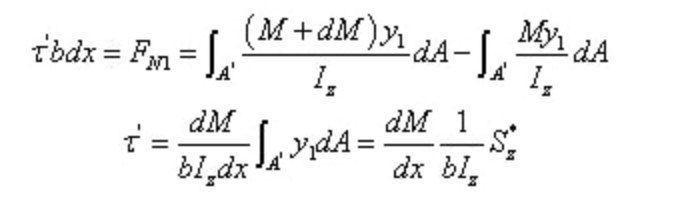
Di antara,

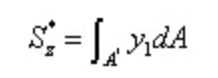
Dari teorema timbal balik tegangan geser dan hubungan diferensial antara gaya geser dan momen lentur:

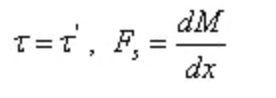
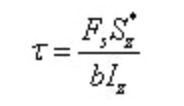
Yang mana:

• b adalah lebar garis horizontal dengan sumbu netral momen y pada bagian tersebut, yang konstan untuk bagian persegi panjang;
• I_z adalah momen inersia sumbu netral dari seluruh penampang melintang;
• S_z* adalah momen statis area di luar garis horizontal yang sumbu netralnya adalah y pada penampang melintang terhadap sumbu netral;
• F_S adalah gaya geser pada penampang melintang.

Di antara,

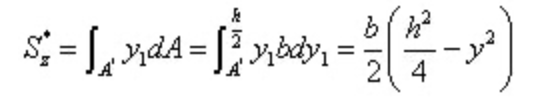
Gantikan ke dalam rumus perhitungan tegangan geser

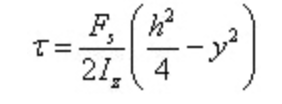
Tegangan geser berbentuk parabola yang terdistribusi di sepanjang tinggi penampang.

Ketika y = 0, terdapat tegangan geser maksimum pada penampang pada sumbu netral

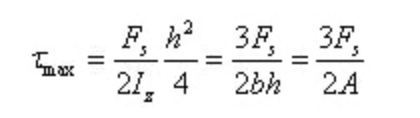
Regangan sudut adalah

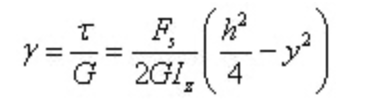
Dapat dilihat bahwa regangan sudut juga terdistribusi secara parabola di sepanjang tinggi penampang.

Pada saat ini, bentuk lengkungan penampang melintang ketika gaya silang menekuk ditunjukkan pada gambar di bawah ini, yang memverifikasi bahwa deformasi tekukan gaya silang tidak memenuhi asumsi bidang.

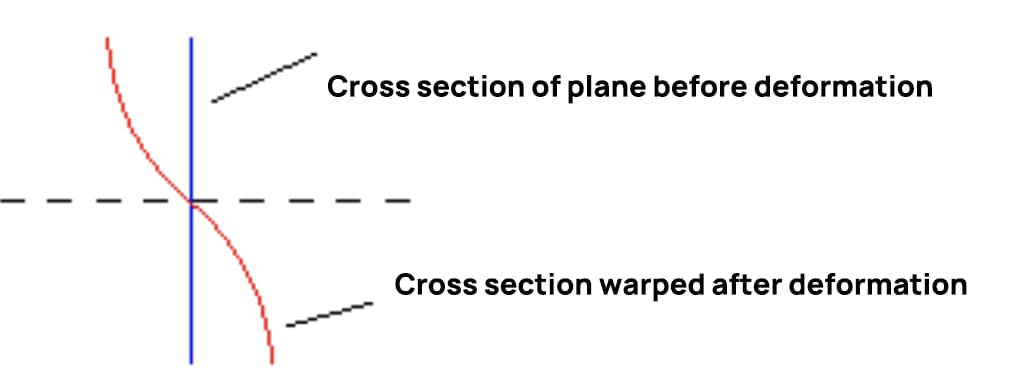
Apabila gaya geser tetap konstan, tegangan geser pada penampang yang berurutan adalah sama, dan tingkat lengkungan juga sama. Panjang serat longitudinal tidak berubah akibat lengkungan penampang, sehingga tidak akan menghasilkan tegangan normal tambahan. Jika gaya geser berubah dengan posisi penampang, derajat lengkungan pada dua penampang yang berurutan akan berbeda, yang menyebabkan tambahan tegangan normal pada penampang.

Untuk penampang simetris dari bentuk lain, solusi tegangan geser perkiraan dapat diturunkan dengan menggunakan metode di atas.

Untuk penampang persegi panjang, dalam rumus penghitungan tegangan, lebar penampang (b) adalah konstan, dan momen statis setengah luas penampang pada satu sisi sumbu netral ke sumbu netral adalah yang terbesar. Akibatnya, tegangan geser pada tiap titik pada sumbu netral adalah yang terbesar.

Untuk penampang simetris dari bentuk lain, tegangan geser maksimum pada penampang biasanya terletak pada berbagai titik pada sumbu netral, dengan pengecualian penampang dengan lebar yang bertambah secara signifikan pada sumbu netral (seperti penampang melintang) atau beberapa penampang dengan lebar bervariasi (seperti penampang segitiga sama kaki).

Oleh karena itu, untuk balok berpenampang I, annular, dan melingkar, tegangan geser maksimum pada setiap titik pada sumbu netral akan dibahas di bawah ini.

Bagian melingkar

Tegangan geser pada setiap titik di tepi bagian lingkaran bersinggungan dengan keliling, sesuai dengan teorema resiprokal tegangan geser. Pada setiap titik sumbu simetri, tegangan geser harus berada pada arah y. Distribusi tegangan geser dapat diasumsikan menyatu pada suatu titik pada sumbu simetri untuk setiap titik sepanjang lebar y dari sumbu netral, dan komponen tegangan geser sepanjang arah Y pada setiap titik sepanjang lebar adalah sama.

Tegangan geser maksimum bagian melingkar masih pada sumbu netral, dan arahnya sejajar dengan gaya eksternal, dengan nilai yang sama pada setiap titik pada sumbu netral.

Tegangan geser maksimum adalah

Penampang melintang berbentuk I

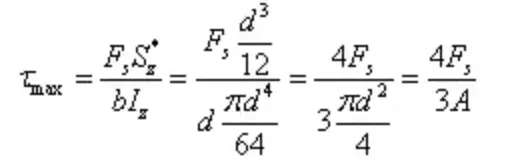
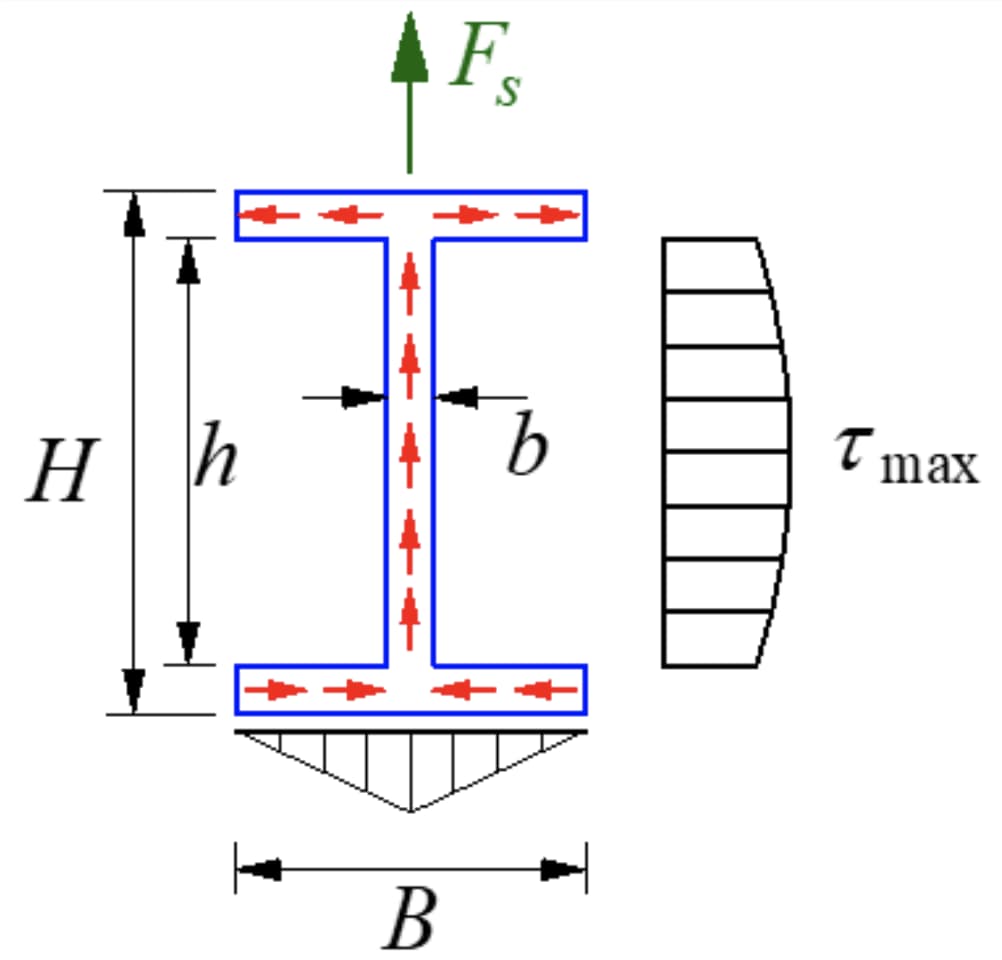
Penampang berbentuk I adalah penampang terbuka berdinding tipis dengan distribusi tegangan seperti yang ditunjukkan pada gambar. Besarnya tegangan geser di sepanjang ketebalan dinding adalah sama, yang dikenal sebagai aliran tegangan geser, mengalir ke arah geser.

Komponen tegangan geser yang sejajar dengan sumbu y pada flens adalah sekunder dan dapat diabaikan, dengan fokus utama pada komponen yang sejajar dengan sisi panjang flens. Tegangan geser pada jaring memiliki distribusi parabola, dengan ukurannya ditunjukkan pada gambar.

Tegangan geser maksimum berada pada sumbu netral.

Dalam hal Baja berbentuk Itegangan geser maksimum:

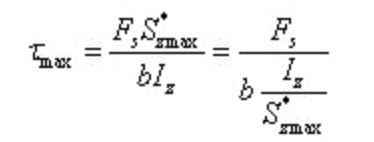
Di mana, b adalah ketebalan jaring, dan I_z/s*_zmax dapat diperoleh dengan mengacu pada tabel baja profil.

Jika penampang berbentuk I yang terdiri dari tiga persegi panjang yang panjang dan sempit, tegangan geser maksimum dan minimum pada jaring dapat diperoleh sebagai berikut:

Dari kedua rumus di atas, terlihat bahwa lebar web jauh lebih kecil daripada lebar flens, sehingga tegangan geser maksimum pada web tidak jauh berbeda dengan tegangan geser minimum.

Oleh karena itu, dapat dianggap bahwa tegangan geser pada jaring secara kasar terdistribusi secara merata.

Tegangan geser yang dihasilkan pada web menyumbang 95-97% dari total gaya geser, dan gaya geser pada penampang sebagian besar ditanggung oleh web.

Karena jaring menanggung hampir semua gaya geser pada penampang, dan tegangan geser pada jaring hampir terdistribusi secara merata, maka tegangan geser maksimum dapat dihitung secara kasar dengan membagi gaya geser dengan luas penampang tiang ventral:

Pada saat yang sama, seluruh area I-beam flens terjauh dari sumbu netral, dan tegangan normal pada setiap titik relatif besar, sehingga flens menanggung sebagian besar momen lentur pada bagian tersebut.

Bagian annular dinding tipis

Ketebalan bagian annular berdinding tipis adalah d, jari-jari rata-rata cincin adalah r, dan ketebalannya jauh lebih kecil daripada jari-jari rata-rata, sehingga dapat diasumsikan bahwa:

Tegangan geser pada penampang sama di sepanjang ketebalan dinding;

Arah tegangan geser bersinggungan dengan garis tengah penampang, dan arah aliran tegangan geser sepanjang arah geser.

Tegangan geser maksimum terletak pada sumbu netral:

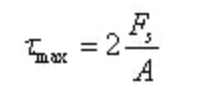
Di mana, A adalah area bagian annular.

Kondisi kekuatan balok

Membengkokkan kondisi kekuatan tegangan normal:

Untuk penampang sumbu simetris netral, tegangan normal tarik maksimum dan tegangan normal tekan maksimum adalah sama.

Bahan plastik yang umum digunakan, dan kondisi kekuatannya:

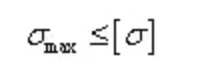
Sedangkan untuk penampang dengan sumbu netral asimetris, tegangan normal tarik maksimum dan tegangan normal tekan maksimum tidak sama.

Bahan yang rapuh umumnya digunakan, dan kondisi kekuatannya:

Kondisi kekuatan tegangan geser lentur adalah:

Langkah-langkah untuk meningkatkan kekuatan lentur balok

Tegangan normal lentur adalah faktor utama yang mengendalikan balok.

Oleh karena itu, kondisi kekuatan lentur tegangan normal sering kali menjadi dasar utama desain balok.

Dari kondisi kekuatan, untuk meningkatkan daya dukung balok, ada dua aspek yang harus dipertimbangkan:

Di satu sisi, tegangan balok harus diatur secara wajar untuk mengurangi momen lentur maksimum;

Di sisi lain, bentuk penampang yang wajar diadopsi untuk meningkatkan koefisien penampang lentur penampang dan memanfaatkan sepenuhnya sifat material.

1. Mengatur tegangan balok secara wajar

Perbaiki kondisi tegangan balok dan coba kurangi momen lentur maksimum pada balok.

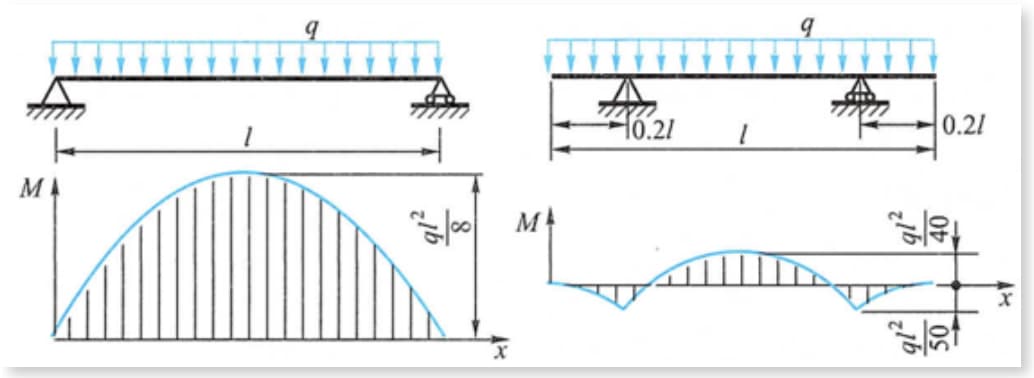
Seperti yang ditunjukkan pada gambar, momen lentur maksimum pada balok di bawah beban seragam sangat berkurang ketika penyangga digerakkan ke dalam dengan jarak tertentu dari posisi kedua ujung balok.

Sebagai contoh, gelagar dan wadah silinder gantry crane, yang titik penopangnya bergerak sedikit ke tengah, dapat mencapai efek mengurangi momen lentur maksimum.

2. Bagian balok yang wajar

Semakin besar koefisien penampang lentur, semakin kecil tegangan dan semakin tinggi daya dukung balok.

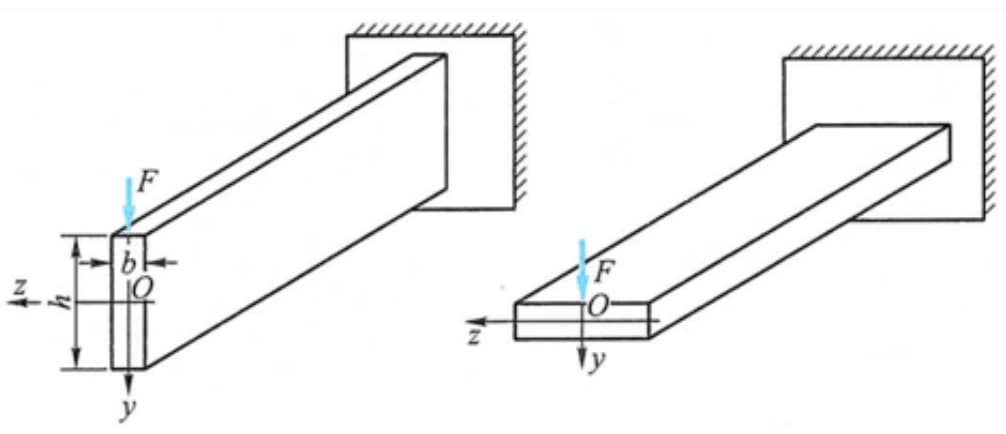
Sebagai contoh, ketika balok dibebani pada arah vertikal, koefisien penampang lentur lebih besar ketika penampang ditempatkan secara vertikal, sehingga lebih masuk akal untuk menempatkannya secara vertikal daripada horizontal.

Sambil meningkatkan koefisien penampang lentur bagian tersebut, kami juga berharap dapat menggunakan lebih sedikit material untuk mencapai ekonomi yang lebih baik.

Oleh karena itu, rasio koefisien penampang lentur terhadap luas penampang pada umumnya digunakan untuk mengukur rasionalitas desain penampang.

Di bawah luas penampang yang sama, penampang persegi panjang (tinggi lebih besar daripada lebar) lebih masuk akal daripada penampang melingkar, sedangkan penampang berbentuk I atau penampang kotak lebih masuk akal daripada penampang persegi panjang.

Oleh karena itu, untuk memanfaatkan sepenuhnya bahan, bahan harus ditempatkan sejauh mungkin dari sumbu netral.

Apabila membahas bentuk bagian yang wajar, maka sifat mekanik material juga harus diperhitungkan.

Material dengan kekuatan tarik dan tekan yang sama (seperti baja karbon rendah) harus menggunakan bagian sumbu simetris netral, seperti lingkaran, persegi panjang, berbentuk I, kotak, dll.

Dengan cara ini, tegangan tarik maksimum dan tegangan tekan maksimum pada tepi atas dan bawah penampang bisa sama.

Untuk material dengan kekuatan tarik dan tekan yang tidak sama (seperti besi tuang, semen, dll.), bentuk penampang dengan sumbu netral yang condong ke sisi tarik harus digunakan.

Konsep balok dengan kekuatan yang sama

Balok yang dibahas di atas semuanya berpenampang sama, dan koefisien penampang lenturnya konstan, tetapi secara umum, momen lentur setiap bagian balok berubah dengan posisi penampang.

Desain penampang balok lurus yang sama harus dilakukan sesuai dengan momen lentur maksimum, dan tegangan maksimumnya mendekati tegangan yang diijinkan.

Momen lentur pada bagian lain kecil, sehingga tegangannya kecil, dan materialnya tidak dimanfaatkan sepenuhnya.

Untuk menghemat bahan dan mengurangi berat sendiri, ukuran penampang dapat diubah sehingga koefisien penampang lentur berubah seiring dengan momen lentur.

Bagian yang lebih besar digunakan apabila momen lentur lebih besar, sedangkan bagian yang lebih kecil digunakan apabila momen lentur lebih kecil.

Balok jenis ini yang penampangnya berubah di sepanjang sumbu disebut balok penampang variabel.

Jika tegangan normal maksimum pada setiap penampang balok penampang variabel sama dengan tegangan ijin, maka balok tersebut disebut balok berkekuatan sama.