Perhitungan Kekuatan Lentur Baja Penampang: Panduan Komprehensif

Bagian Satu: Pendahuluan

1. Konsep:

Mendukung beban lateral seperti balok lantai, balok derek, purlins, jembatan, dll.

2. Klasifikasi:

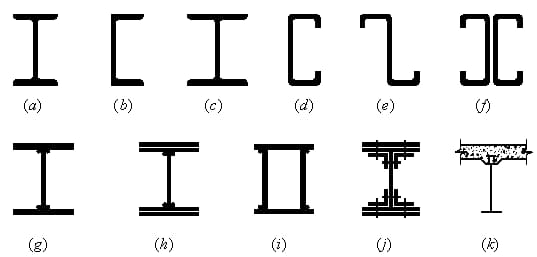
(1) Web yang kokoh: (1) Web yang kokoh: (2)

Bagian baja berbentuk H: Mudah diproses, mudah dibuat, dan berbiaya rendah.

Bagian komposit: Jika baja berbentuk H tidak dapat memenuhi persyaratan kekuatan dan kekakuan.

(2) Struktur kisi-kisi:

Apabila bentangnya melebihi 40m, yang terbaik adalah menggunakan rangka kisi-kisi.

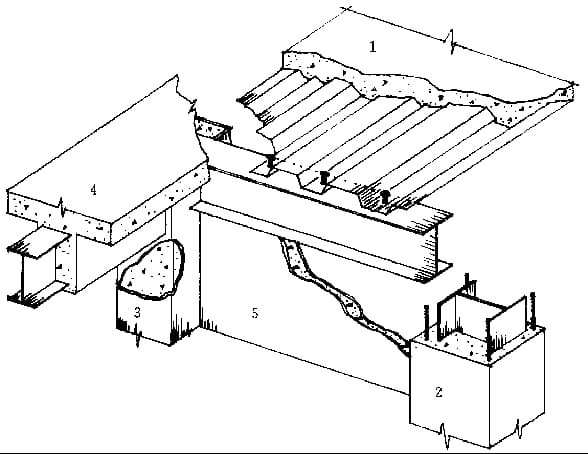
3. Kisi-kisi balok:

Sistem planar yang terdiri dari balok utama dan sekunder yang berpotongan secara vertikal dan horizontal.

(1) Kisi-kisi balok yang disederhanakan: Balok utama tunggal.

(2) Kisi-kisi balok biasa: Dibagi menjadi balok utama dan balok sekunder.

(3) Kisi-kisi balok majemuk: Dibagi menjadi balok utama, balok sekunder horizontal dan vertikal.

4. Interaksi antara balok dan pelat:

(1) Kerja bersama: Pelat lantai komposit.

(2) Pekerjaan non-kooperatif: Pelat beton bertulang umum.

Bagian Dua: Kekuatan Lentur.

Perkembangan tegangan normal pada penampang dapat dibagi menjadi tiga tahap:

(1) Tahap elastis: Di bawah beban dinamis.

(2) Tahap elastis-plastik: Di bawah beban statis atau beban dinamis tidak langsung.

(3) Panggung plastik:

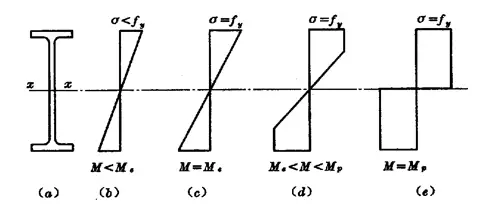
Kapasitas lentur selama tahap elastis-plastis dari penampang melintang:

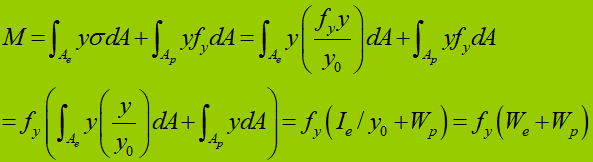
Untuk bagian persegi panjang:

(1) Tahap elastis:

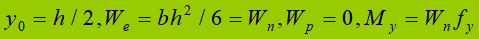
(2) Panggung plastik:

(3) Tahap elastis-plastik:

Faktor bentuk bagian:

Bagian Ketiga: Rumus Perhitungan Kekuatan yang Diadopsi oleh Kode.

I. Membengkokkan tegangan normal:

Pengembangan plastis bagian parsial (1/4 bagian, a = h/8) sebagai kondisi batas:

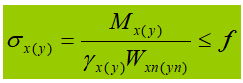
Dalam rumus:

γ adalah faktor keamanan parsial untuk momen, yang dapat ditentukan berdasarkan Tabel 5.1 pada Bagian 5 dari kode desain.

Ada dua kasus di mana faktor keamanan parsial untuk momen harus diambil sebagai 1,0.

II. Kekuatan geser:

Metode:

S:

Kekuatan geser dapat dihitung dengan menggunakan teori aliran geser, dengan asumsi bahwa kekuatan geser terdistribusi secara seragam di sepanjang arah ketebalan dinding tipis.

(1) Ketika menghitung tegangan geser vertikal pada titik manapun pada web, perlu dihitung momen inersia luas penampang bruto di atas atau di bawah titik tersebut sehubungan dengan sumbu netral x.

(2) Saat menghitung tegangan geser horizontal pada titik mana pun pada flens, perlu dihitung momen inersia area dari bagian bruto di sebelah kiri atau kanan titik tersebut sehubungan dengan sumbu netral x.

Di mana t_w adalah ketebalan penampang pada lokasi di mana tegangan geser dihitung.

III. Tegangan tekuk lokal pada jaring:

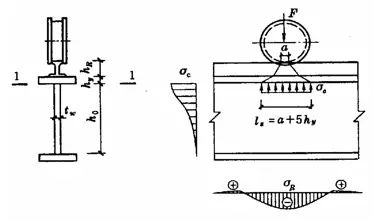
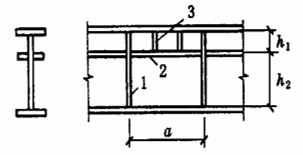
Bila flens balok dikenai beban terpusat tetap yang besar (termasuk reaksi sokongan) dan tidak ada pengaku yang disediakan sesuai dengan Gambar 5-5(a), atau bila dikenai beban terpusat yang bergerak (seperti tekanan roda derek) sesuai dengan Gambar 5-5(b), maka kuat tekan lokal di tepi tinggi web harus dihitung. Dengan mengasumsikan bahwa beban terkonsentrasi menyebar dari titik aplikasi ke kisaran ketinggian h_y dengan rasio 1:2,5, dan menyebar dengan rasio 1:1 dalam kisaran ketinggian h_Rdidistribusikan secara merata di atas ketinggian jaring perhitungan tepi. σ yang dihasilkan_c sangat dekat dengan tekanan lokal teoritis maksimum. Kekuatan tekan lokal dapat dihitung dengan rumus berikut:

Dalam rumus,

• F - beban terkonsentrasi, yang harus dikalikan dengan koefisien dinamis untuk beban dinamis;
• ψ - faktor penguatan beban terkonsentrasi. Untuk tekanan roda derek tingkat kerja tugas berat, ψ = 1,35; untuk beban lainnya, ψ = 1,0;
• l_z - panjang distribusi yang diasumsikan dari beban terkonsentrasi pada ketinggian pelat web yang dihitung. Untuk beban terkonsentrasi pada pertengahan bentang, l_z= a + 5 jam_y+2h_Runtuk gaya reaksi penyangga ujung balok, l_z= a + 2,5 jam_y+a₁;
• a - panjang tumpuan dari beban terkonsentrasi di sepanjang arah bentang. Untuk tekanan roda derek, jika tidak ada data yang tersedia, maka dapat diambil sebagai 50mm;
• h_y - jarak dari bagian atas balok ke ketinggian pelat web yang dihitung;
• h_R - ketinggian lintasan. Jika tidak ada lintasan di bagian atas balok, h_R=0;
• a₁ - jarak dari ujung balok ke tepi luar pelat penyangga, dan nilainya tidak boleh lebih besar dari 2,5 jam_y.

Ketika perhitungan tidak memuaskan, beban atau dukungan terkonsentrasi tetap bantalan dapat diperkuat dengan mengatur pengaku melintang atau memodifikasi ukuran penampang. Namun, ketika menanggung beban terkonsentrasi yang bergerak, hanya ukuran penampang yang dapat dimodifikasi.

IV. Tegangan ekuivalen di bawah kondisi tegangan yang kompleks.

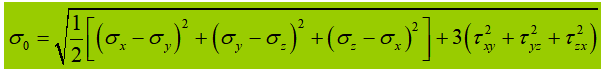
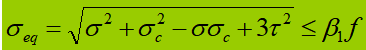
Ketika vibrator perut mengalami tegangan normal, tegangan geser, atau tegangan tekan lokal yang signifikan pada ketinggian yang dihitung, tegangan ekuivalen di lokasi tersebut perlu dihitung.

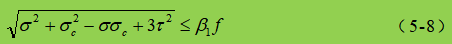
Dalam rumus:

σ, τ, σ_c - tegangan normal lentur, tegangan geser, dan tegangan tekan lokal pada titik yang sama pada ketinggian perhitungan pelat perut, positif untuk tegangan tarik dan negatif untuk tegangan tekan;

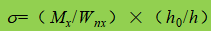
β₁ - koefisien untuk meningkatkan nilai desain kuat tekan pada suatu titik lokal. Bila σ dan σc memiliki tanda yang sama atau σ_c=0, β₁=1.1; ketika σ dan σc memiliki tanda yang berlawanan, β₁=1.2.

Bagian Empat: Perhitungan Stabilitas Keseluruhan Balok

1. Konsep Dasar

Fenomena ketidakstabilan secara keseluruhan:

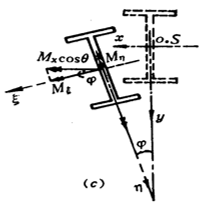
Analisis mekanisme: 

Setelah balok mengalami deformasi akibat tekukan, flens atas mengalami kompresi. Karena kekakuan lateral balok yang tidak mencukupi, balok akan mengalami deformasi tekuk lateral. Deformasi lentur pada bidang yang disebabkan oleh momen juga terjadi bersamaan dengan deformasi puntir akibat tekukan yang tidak sama dari atas ke bawah penampang balok.

Oleh karena itu, ketidakstabilan keseluruhan balok mengambil bentuk tekuk lentur-torsi, atau lebih tepatnya, tekuk lateral dan tekuk puntir.

2. Rumus Perhitungan Momen Lentur Kritis Balok Bertumpu Sederhana dengan Penampang Simetris Uniaksial:

(1) C1, C2, C3 - Terkait dengan jenis beban

(2) Iy, Iw, It - Momen inersia penampang melintang

(3) L - Panjang yang tidak dikunci pada arah lateral

(4) a - Lokasi titik aksi pada arah ketinggian.

(5)

Faktor utama yang mempengaruhi stabilitas keseluruhan balok baja adalah:

(1) Panjang tak terkekang pada arah lateral atau jarak L1 antara titik tumpuan lateral flens tekan. Semakin kecil nilai L1, semakin baik stabilitas keseluruhan balok dan semakin tinggi momen lentur kritisnya.

(2) Ukuran penampang, termasuk berbagai momen inersia. Semakin besar momen inersia, semakin baik stabilitas balok secara keseluruhan. Khususnya, meningkatkan lebar flens tekan b1 juga dapat meningkatkan nilai βy dalam rumus.

(3) Kendala pada penampang oleh sokongan ujung balok. Jika batasan rotasi di sekitar sumbu y penampang dapat ditingkatkan, maka stabilitas balok secara keseluruhan akan sangat meningkat.

(4) Tipe pemuatan: Pembengkokan murni, beban terdistribusi seragam, beban terkonsentrasi pada pertengahan bentang.

(5) Lokasi titik kerja beban sepanjang arah ketinggian penampang, nilai; negatif untuk flens atas dan positif untuk flens bawah.

3. Verifikasi Stabilitas Keseluruhan

Pembengkokan bidang tunggal:

4. Koefisien Stabilitas Keseluruhan

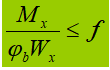
1. Penampang melintang berbentuk I yang dilas, simetris biaksial, murni beban lentur.

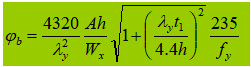
2. Penampang melintang berbentuk I yang dilas, simetris uniaksial (efek penampang melintang asimetris dan beban yang berbeda)

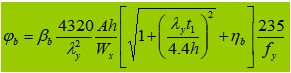
Jika φ_b>0,6, koefisien stabilitas diambil sebagai:

3. Baja berbentuk I biasa yang digulung dengan balok penyangga sederhana.

4. Baja saluran canai panas yang hanya ditopang balok.

5. Balok kantilever berbentuk I simetris sumbu ganda.

5. Memastikan stabilitas secara keseluruhan.

Flensa balok yang dikompresi ditutup dengan penghiasan (beton bertulang atau pelat baja) dan terhubung dengan kuat untuk mencegah perpindahan lateral flensa yang dikompresi.

Untuk balok H atau balok I yang ditumpu secara sederhana, rasio panjang bebas L1 terhadap lebar b dari flens yang dikompresi tidak melebihi nilai yang ditentukan dalam Tabel 5.4.

Tabel 5.4: Nilai maksimum L1/b1 yang tidak memerlukan perhitungan stabilitas keseluruhan untuk balok H atau balok I yang ditumpu secara sederhana.

6. Langkah-langkah verifikasi untuk stabilitas keseluruhan:

1. Tentukan apakah verifikasi stabilitas secara keseluruhan diperlukan.

2. Hitung parameter bagian.

3. Dapatkan koefisien momen lentur kritis ekuivalen βb sesuai dengan kondisi beban.

4. Substitusikan nilai-nilai tersebut ke dalam rumus untuk mendapatkan koefisien stabilitas keseluruhan ϕb, dan verifikasi stabilitas keseluruhan.

Contoh: 5-2，5-3

Bagian 5 - Stabilitas lokal dan desain pengaku balok

1. Gambaran umum:

Pelat Flange: Beban relatif sederhana, dan stabilitas lokal dijamin dengan membatasi rasio lebar-ke-tebal pelat.

Web Plate: Bebannya kompleks dan untuk memenuhi persyaratan kekuatan, tinggi penampang sering kali besar. Jika kita terus membatasi rasio tinggi-ke-ketebalan pelat web, nilai pelat web akan sangat besar sehingga tidak ekonomis. Oleh karena itu, pengaku umumnya digunakan untuk mengurangi ukuran pelat dan meningkatkan daya dukung stabilitas lokal.

1. Pengaku melintang

2. Pengaku longitudinal

3. Pengaku pendek

2. Stabilitas lokal pelat flensa sayap.

Prinsip desain: Prinsip kekuatan yang sama.

Menurut desain elastis (dengan γ = 1,0 untuk tidak mempertimbangkan pengembangan plastik), karena pengaruh tegangan sisapenampang yang sebenarnya telah memasuki tahap elastis-plastik. "Spesifikasi" mengambil E_t=0.7E.

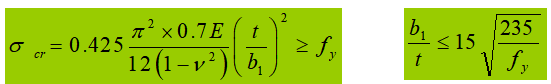
Jika pengembangan plastis dipertimbangkan (γ > 1,0), pengembangan plastis akan lebih besar, dan E_t=0.5E.

3. Tekuk pelat web

Tidak.	Kondisi pelat web.		Spesifikasi pengaturan pengaku
1		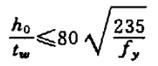στ=0	Pengaku bisa dihilangkan.
2		στ≠0	Direkomendasikan untuk memasang pengaku melintang yang memenuhi persyaratan struktural dan perhitungan.
3			Direkomendasikan untuk memasang pengaku melintang yang memenuhi persyaratan struktural dan perhitungan.
4	Flensa yang dikompresi tertahan dari puntiran.		Pengaku longitudinal harus ditambahkan pada zona kompresi pada bagian yang memiliki tegangan lentur tinggi, memenuhi persyaratan struktural dan perhitungan.
5	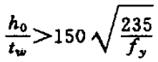Flensa yang dikompresi bebas diputar.
6	Bila diperlukan untuk tujuan perhitungan.
7	Ketika tegangan tekan lokal tinggi.		Jika perlu, pengaku pendek harus diatur di zona kompresi untuk memenuhi persyaratan struktural dan perhitungan.
8	Pada penyangga balok		Disarankan untuk memasang pengaku pendukung yang memenuhi persyaratan struktural dan perhitungan.
9	Di mana flensa mengalami beban terkonsentrasi tetap yang besar.
10	Dalam hal apapun		h0/tw tidak boleh melebihi

1. Tekuk pelat bertekanan komposit

Hanya pelat web dengan pengaku melintang yang dikonfigurasikan.

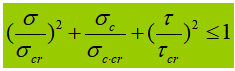
Pelat web dikonfigurasikan dengan pengaku melintang dan memanjang secara bersamaan.

(1) Antara flens yang dikompresi dan pengaku longitudinal.

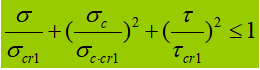
(2) Antara flensa tegangan dan pengaku longitudinal.

Pengaku melintang pendek dipasang di antara flens yang dikompresi dan pengaku longitudinal.

2. Persyaratan konstruksi pengaku untuk pelat web

(1) Pengaku melintang baja yang dikonfigurasikan berpasangan di kedua sisi pelat web.

Lebar yang menonjol ke luar:

Ketebalan:

(2) Pengaku melintang baja yang dikonfigurasikan pada satu sisi pelat web.

Lebar yang menonjol ke luar: harus lebih besar dari 1,2 kali nilai yang dihitung menurut rumus di atas.

Ketebalan: tidak boleh kurang dari 1/15 dari lebarnya yang menonjol ke luar.

(3) Pada pelat web yang diperkuat dengan pengaku melintang dan memanjang, pengaku memanjang harus diputuskan pada perpotongannya sementara pengaku melintang tetap kontinu.

Momen inersia di sekitar sumbu-z juga harus memuaskan:

(4) Perawatan ujung pengaku melintang:

3. Pengaku untuk penyangga

(1) Perhitungan stabilitas:

Stabilitas pengaku untuk sokongan dihitung sebagai member kompresi yang dikenai beban terkonsentrasi tetap atau reaksi sokongan balok di sepanjang sumbunya. Luas penampang A dari member kompresi ini mencakup pengaku dan luas pelat web dalam 15t_w pada setiap sisi pengaku. Panjang perhitungan kira-kira diambil sebagai h0.

(2) Perhitungan kekuatan tekan:

Ujung pengaku penyangga untuk balok harus dihitung sesuai dengan beban terkonsentrasi tetap atau reaksi penyangga yang dipikulnya. Bila ujung pengaku dipangkas rata dan rapat, tegangan tekan pada permukaan ujung harus dihitung sebagai berikut:

dimana:

• f_ce adalah nilai desain kekuatan kompresi permukaan ujung baja;
• A_ce adalah area di mana pengaku penyangga menyentuh pelat flensa atau tutup kolom.

Langkah-langkah desain untuk pengaku melintang pelat web:

1. Tentukan apakah palang perlu dipasang;

2. Pasang palang dan tentukan jarak a, bs, ts;

3. Verifikasi status tegangan komposit pelat web;

4. Verifikasi pengaku penyangga: termasuk pengelasan (sambungan antara palang dan pelat web), verifikasi stabilitas kompresi aksial (stabilisasi di luar bidang sumbu-z), dan verifikasi kekuatan.

Contoh 5-3: Berdasarkan kondisi dan hasil pada Contoh 5-2, verifikasi apakah penampang balok utama yang ditunjukkan pada Gambar 5-9(b) memenuhi persyaratan. Balok utama adalah balok yang ditumpu secara sederhana pada kedua ujungnya, terbuat dari baja Q235 dan dilas dengan elektroda las manual seri E43.

Solusi:

1. Daya dukung beban balok utama:

Diagram perhitungan yang disederhanakan dari balok utama ditunjukkan pada Gambar 5-9(a). Tekanan yang diberikan pada balok utama oleh balok sekunder di kedua sisinya adalah 2×73.69+2×2.33=152.04 kN, dan tekanan balok sekunder di ujung balok adalah setengah dari tekanan balok sekunder tengah.

Reaksi tumpuan balok utama adalah R = 2 × 152,04 = 304,08 kN.

Momen lentur maksimum balok adalah M = (304.08-76.02) x5-152.04 × 2.5 = 760.2 kN.m

2. Hitung karakteristik bagian:

A = 131,2 cm², I_x=145449 cm⁴, W_x=3513,3 cm³. Berat sendiri balok utama adalah 131,2×10²x7850x10-⁶x1,2 = 123,6 kg/m = 1,211 kN/m. Faktor 1,2 adalah untuk mempertimbangkan peningkatan koefisien pengaku balok utama. Nilai desain momen lentur setelah mempertimbangkan berat balok utama adalah M = 760.2+1.2×1.211×10²/8=760.2+18.2=778.4 kN-m.

Mempertimbangkan nilai desain gaya reaksi pada penyangga setelah memperhitungkan berat sendiri balok utama adalah R = 304.08+1.2×1.211×10/2=304.08+7.27=311.3kN.

3. Pemeriksaan kekuatan

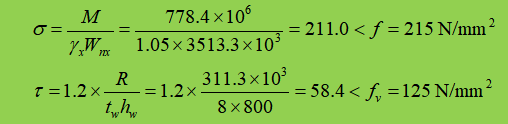
Pengaku pendukung disediakan pada sambungan balok sekunder, dan tidak ada tegangan tekan lokal. Selain itu, karena tegangan geser relatif kecil, maka tidak perlu memverifikasi tegangan yang dikonversi pada bagian lain.

4. Terdapat pelat kaku pada balok sekunder, yang menjamin stabilitas balok sekunder dan dapat berfungsi sebagai titik penyangga lateral balok utama.

Pada titik ini, karena l₁/b₁=2500/240 = 10,4 <16, stabilitas keseluruhan dapat dipastikan tanpa perhitungan.

5. Pemeriksaan kekakuan

Nilai standar total beban yang ditransmisikan oleh sinar sekunder adalah F_T=(15.5+0.52)×7.5=120.2kN, therefore,

Nilai standar total beban yang ditransmisikan oleh sinar sekunder adalah F_Q=2.5×4.2×7.5=78.75kN, therefore,

6. Stabilitas lokal

Flensa: b/t = (120-4) / 14 = 8,3 <13, yang memenuhi persyaratan stabilitas lokal, dan γ_x dapat diambil sebagai 1,05; Pelat web: h₀/t_w=800/8=100, pengaku melintang harus disediakan, detail dihilangkan.

Bagian 6. Kekuatan setelah Tekuk Pelat Tipis

1. Konsep dan analisis kekuatan setelah tekuk pelat tipis:

Setelah pelat tipis melengkung, tegangan tarik melintang dihasilkan di tengah pelat, yang selanjutnya membatasi deformasi tekukan longitudinal pelat, sehingga memungkinkan pelat untuk terus menahan tekanan yang meningkat.

2. Analisis Daya Dukung Geser Pelat Web dengan Mempertimbangkan Kekuatan Setelah Tekuk:

1. Daya dukung geser setelah tekuk: Rumus (5-94)

2. Daya dukung geser mencakup dua bagian: Gaya geser tekuk (kekuatan tekuk) + gaya geser bidang tegangan (kekuatan setelah tekuk).

3. Gaya geser bidang tegangan:

(1) Metode medan tegangan (kompleks);

(2) Spesifikasi kode.

3. Analisis Daya Dukung Lentur Pelat Web dengan Mempertimbangkan Kekuatan Setelah Tekuk:

Mempertimbangkan bahwa daya dukung lentur pelat web sedikit berkurang setelah tekuk.

Dua asumsi:

(1) Ketinggian efektif;

(2) Simetri antara zona tegangan dan zona kompresi.

Rumus untuk menghitung daya dukung:

4. Rumus perhitungan untuk balok yang mempertimbangkan kekuatan setelah tekuk (secara bersamaan mengalami momen lentur dan gaya geser):

Dalam rumus,

• M dan V adalah nilai desain momen lentur dan gaya geser pada penampang balok yang sama
• Ketika V < 0,5Vu, ambil V = 0,5Vu
• Ketika M < M_f, ambil M = M_f

Hal ini mengindikasikan hal tersebut:

(1) Ketika M pada bagian tersebut kurang dari M_f bahwa flensa dapat bertahan, pelat web dapat menahan gaya geser Vu;

(2) Ketika V pada bagian tersebut kurang dari 0,5Vu, ambil M = M_eu.

5. Desain Pengaku Melintang Mempertimbangkan Kekuatan Pasca-Tekuk

(1) Jika pengaku penyangga saja tidak dapat memenuhi Persamaan (5.99), pengaku melintang berpasangan harus ditambahkan pada kedua sisi web untuk mengurangi panjang daerah tekuk.

(2) Dimensi penampang pengaku melintang harus memenuhi persyaratan konstruksi untuk pengaku web sesuai Persamaan 5.85.

(3) Menurut spesifikasi struktur baja, pengaku melintang pusat harus diperlakukan sebagai anggota kompresi aksial dan stabilitasnya di luar bidang web harus dihitung berdasarkan gaya aksial dengan menggunakan rumus berikut:

Ketika pengaku dikenai beban melintang terkonsentrasi F, Ns harus ditingkatkan sebesar F.

Bagian 7. Desain Balok Baja

1. Desain Balok Baja Gulung

Hitung nilai desain dari momen lentur maksimum M_maks untuk balok berdasarkan kondisi aktual.

Tentukan modulus penampang yang diperlukan berdasarkan kekuatan lentur dan stabilitas keseluruhan:

Tentukan penampang baja berdasarkan tabel penampang.

Verifikasi bagian tersebut:

(1) Verifikasi kekuatan: lentur, geser, kompresi lokal, dan tegangan ekuivalen.

(2) Verifikasi kekakuan: verifikasi rasio defleksi terhadap bentang balok.

(3) Verifikasi stabilitas secara keseluruhan (stabilitas lokal bagian baja biasanya tidak memerlukan verifikasi).

(4) Sesuaikan bagian berdasarkan hasil verifikasi, dan lakukan verifikasi lagi sampai memenuhi persyaratan desain.

2. Desain Penampang Balok Komposit

1) Tentukan modulus penampang yang diperlukan berdasarkan kondisi beban.

2) Tentukan tinggi balok:

• Tinggi minimum: h_min ditentukan oleh kekakuan balok.
• Tinggi maksimum: h_maks ditentukan oleh persyaratan desain arsitektur.
• Tinggi ekonomis: h_e ditentukan oleh konsumsi baja minimum.

Ketinggian yang dipilih: h_min ≤ h ≤ h_maks.

3). Tentukan ketebalan jaring (dengan asumsi bahwa semua gaya geser ditanggung oleh jaring), kemudian:

Sebagai alternatif, ketebalan jaring dapat ditentukan dengan menggunakan rumus empiris:

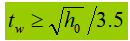
4). Tentukan lebar flensa:

Setelah menentukan ketebalan web, area flensa A_f dapat ditentukan berdasarkan persyaratan kekuatan tekuk. Mengambil penampang berbentuk I sebagai contoh:

Setelah A_f ditentukan, baik b atau t dapat dipilih untuk menentukan nilai lainnya.

5). Verifikasi bagian tersebut:

• Verifikasi kekuatan: lentur, geser, kompresi lokal, dan kekuatan tegangan ekuivalen.
• Verifikasi kekakuan: verifikasi rasio defleksi terhadap bentang balok.
• Verifikasi stabilitas secara keseluruhan.
• Verifikasi stabilitas lokal (pelat flensa).
• Sesuaikan bagian tersebut berdasarkan hasil verifikasi, dan lakukan verifikasi lagi sampai memenuhi persyaratan desain.
• Hitung dan susunlah pengaku sesuai dengan kondisi aktual.

6). Perhitungan Lasan antara Web dan Flange

Las sambungan terutama digunakan untuk menahan geser lenturdan geseran per satuan panjang adalah:

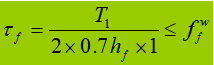
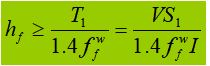
Ketika balok dikenai beban terkonsentrasi tetap tanpa pengaku penyangga, las flens atas memikul kedua gaya geser T₁ dan gaya terkonsentrasi F. Gaya per satuan panjang yang dihasilkan oleh F adalah V₁:

3. Perubahan Bagian untuk Balok Komposit yang Dilas

Tujuan: Untuk menghemat baja dan menangani perubahan momen lentur.

Metode perubahan bagian:

• Mengubah lebar flensa.
• Mengubah ketebalan flensa atau jumlah lapisan.
• Mengubah tinggi dan ketebalan jaring.

Hal-hal yang perlu diperhatikan:

• Metode ini hanya digunakan untuk bentang panjang.
• Perubahan bagian harus dilakukan secara bertahap untuk mencegah konsentrasi tegangan yang parah.
• Tegangan ekuivalen harus diverifikasi.

Bagian 8. Penyambungan Balok Baja

1. Klasifikasi:

• Penyambungan pabrik: Dilakukan di lingkungan yang terkendali untuk kualitas yang optimal.
• Penyambungan di tempat: Digunakan ketika ada keterbatasan transportasi atau penanganan.

2. Metode penyambungan untuk bagian baja yang digulung:

• Pengelasan pantat: Pengelasan penetrasi penuh untuk kekuatan maksimum dan penampilan yang mulus.
• Pengelasan pelat sambungan: Menggunakan pelat tambahan untuk menyambung bagian balok, menawarkan fleksibilitas dalam desain dan perakitan di lapangan yang lebih mudah.

3. Teknik penyambungan balok komposit:

• Penyambungan pabrik: Jaring dan flensa dibuat terhuyung-huyung untuk mendistribusikan tegangan dan mempertahankan integritas struktural.
• Penyambungan di tempat: Web dan flensa disambung pada bagian yang sama untuk menyederhanakan perakitan di lapangan dan mengurangi waktu konstruksi.

Pertimbangan utama:

• Lokasi sambungan: Posisikan sambungan secara strategis di area dengan tegangan lentur yang relatif rendah untuk meminimalkan dampak struktural.
• Kontrol kualitas: Pengelasan di tempat menghadirkan tantangan dalam menjaga kualitas yang konsisten karena faktor lingkungan dan masalah aksesibilitas.
• Pengujian non-destruktif: Menerapkan protokol pemeriksaan yang ketat, seperti pengujian ultrasonik atau radiografi, untuk memastikan integritas sambungan.
• Transfer beban: Sambungan desain untuk mentransfer semua beban yang diantisipasi secara efektif, termasuk gaya aksial, geser, dan momen.

Bagian 9. Sambungan Balok Baja Primer dan Sekunder dan Penyangga Balok

1. Sambungan balok baja primer dan sekunder:

• Koneksi yang tumpang tindih: Memberikan transfer geser yang sangat baik dan ereksi yang disederhanakan.
  - Sambungan duduk: Balok sekunder bertumpu pada sudut rak yang dilas ke balok primer.
  - Sambungan flens flensa atas dan bawah: Menawarkan ketahanan momen yang ditingkatkan.
• Sambungan sambungan pantat: Ideal untuk pengaturan balok rata dan persyaratan kedalaman yang seragam.
  - Sambungan pelat ujung: Pelat yang dibaut atau dilas pada ujung balok untuk penyelarasan yang tepat.
  - Sambungan pelat sirip: Sederhana dan ekonomis untuk mentransfer beban geser.

2. Jenis penyangga balok:

• Penyangga pelat datar:
  - Sederhana dan hemat biaya untuk beban sedang.
  - Menyediakan permukaan bantalan yang seragam dan pemasangan yang mudah.
• Penyangga berbentuk busur:
  - Mendistribusikan beban secara lebih merata, mengurangi konsentrasi tegangan.
  - Ideal untuk beban berat atau di mana gerakan rotasi diantisipasi.
• Penyangga berengsel:
  - Memungkinkan gerakan rotasi, mengakomodasi ekspansi dan kontraksi termal.
  - Mengurangi transfer momen ke struktur pendukung.

Pertimbangan desain utama:

• Kapasitas beban: Pilih jenis penyangga berdasarkan beban yang diantisipasi dan persyaratan struktural.
• Kemampuan konstruksi: Pertimbangkan kemudahan pemasangan dan potensi prefabrikasi.
• Kemudahan servis: Sambungan dan penyangga yang didesain untuk memudahkan pemeliharaan atau modifikasi di masa mendatang.
• Perlindungan korosi: Menerapkan tindakan perlindungan yang tepat, khususnya untuk sambungan yang terbuka.