Analisis Kelelahan Berdasarkan Kurva S-N: Memecahkan Masalah Dasar

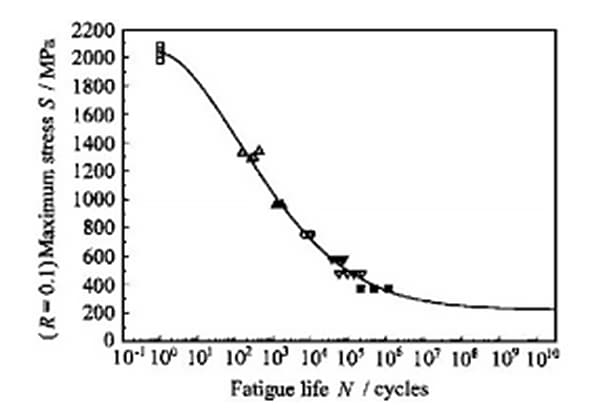
Sifat fatik material biasanya diekspresikan melalui siklus tegangan uniaksial, yang dikenal sebagai kurva S-N. Penting untuk dicatat bahwa teori fatik yang didasarkan pada mekanika patah tidak dipertimbangkan dalam konteks ini.

Variasi tegangan dari waktu ke waktu sering kali mengikuti pola yang teratur, seperti gelombang sinus, gelombang persegi, atau denyut nadi. Namun, pengaruh stres rata-rata terhadap kinerja kelelahan sering diabaikan (yaitu, dampak dari r = S_min/S_maks ≠ -1).

Pada kenyataannya, kondisi tegangan biasanya bersifat multiaksial, dengan variasi tegangan yang tidak beraturan dan r≠-1. Korespondensi antara stres aktual dan kinerja kelelahan yang diukur di laboratorium, yang melibatkan variasi stres reguler, stres uniaksial, dan r = 1, menjadi dasar analisis kelelahan.

1. Perlakuan terhadap pengaruh stres rata-rata

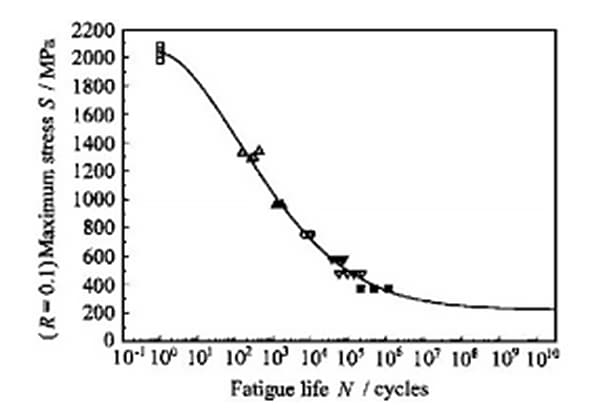
Apabila terdapat kurva S-N yang tersedia untuk nilai r yang berbeda, metode interpolasi biasanya digunakan untuk menentukan kurva S-N untuk nilai r yang tidak diketahui.

Dalam kasus di mana hanya kurva S-N dengan r = -1 yang tersedia, rumus berikut dapat digunakan untuk menghitung tegangan ekuivalen. Rumus ini mengubah tegangan uniaksial r≠-1 menjadi tegangan uniaksial ketika r=-1, yang dikenal sebagai tegangan ekuivalen:

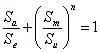
Di mana, S_a adalah setengah amplitudo tegangan, S_e adalah tegangan ekivalen yang diinginkan, S_m adalah tegangan rata-rata, dan nilai yang berbeda dari S_u dan n merupakan teori yang berbeda:

• Tegangan leleh Soderberg (sy) 1
• Tegangan tarik utama Goodman (su) 1
• Tegangan tarik ultimit Gerber (su) 2
• Tegangan patah sejati besok (sf) 1

2. Konversi tegangan multiaksial menjadi tegangan uniaksial

Pilihan tegangan berikut ini tersedia untuk menentukan jenis tegangan yang digunakan untuk transformasi: Tegangan ekuivalen Von Mises, tegangan geser maksimum, tegangan utama maksimum, atau komponen tegangan tertentu (seperti Sx, Syz, dll.).

Kadang-kadang, tegangan Mises dengan tanda juga digunakan, dengan besarannya tetap tidak berubah. Tanda tersebut sesuai dengan tanda tegangan utama maksimum. Satu keuntungan dari metode ini adalah, bahwa metode ini memungkinkan untuk mempertimbangkan efek tegangan atau kompresi, yang tercermin dalam tegangan rata-rata atau r.

Mirip dengan teori kekuatantegangan ekuivalen Von Mises dan konversi tegangan geser maksimum sesuai untuk material dengan keuletan tinggi, sedangkan konversi tegangan prinsipal maksimum sesuai untuk material yang rapuh.

3. Pengobatan stres yang tidak teratur

Kurva waktu tegangan uniaksial ekuivalen dengan tinggi dan rendah yang tidak beraturan dianalisis untuk mengekstrak serangkaian siklus tegangan sederhana (S_a, S_m) dan waktu yang sesuai.

Penghitungan dan statistik dapat dilakukan dengan menggunakan berbagai metode, termasuk metode path dependent dan metode path independent.

Metode korelasi jalur, yang merupakan metode penghitungan aliran hujan yang paling banyak digunakan, diterapkan untuk menyelesaikan proses penghitungan. Algoritme dan prinsipnya dijelaskan dalam "Downing, S., Society, D. (1982) Simplified rain flow counting algorithms. Int J Fatigue, 4, 31 - 40".

Setelah perlakuan aliran hujan, kurva waktu tegangan yang tidak beraturan diubah menjadi serangkaian siklus sederhana (S_a, S_m, dan n_idengan ni adalah jumlah siklus).

Metode ini memungkinkan penerapan teori akumulasi kerusakan (kriteria Miner) untuk menghitung dan menganalisis: Jumlah (n_i/N_i), di mana Ni adalah umur yang sesuai dengan siklus tegangan (dengan mempertimbangkan S_a, S_mlihat di atas).

Teknik ini biasanya digunakan untuk mengukur faktor keamanan setelah sejumlah siklus tertentu atau masa pakai yang sesuai dari siklus tegangan kompleks tertentu.

Saat ini, perangkat lunak analisis kelelahan komersial sebagian besar didasarkan pada proses yang disebutkan di atas.

Namun, perlu dicatat bahwa analisis kelelahan adalah analisis empiris, dan teori yang matang dan lengkap saat ini belum ada.

Terdapat berbagai perspektif mengenai konversi tegangan multiaxial menjadi tegangan uniaksial.

Tegangan Von Mises, misalnya, adalah besaran dimensi tegangan yang didasarkan pada gagasan tentang energi spesifik perubahan bentuk.

Menggunakan konsep positif dan negatif atau ketegangan dan kompresi adalah metode yang tidak tepat, dan tidak direkomendasikan.

Pemilihan jenis tegangan yang akan diadopsi tergantung pada kemungkinan tren keretakan pada material atau struktur untuk menentukan jenis tegangan mana yang menjadi faktor utama yang mengendalikan kegagalan kelelahan.

Praktik rekayasa telah menunjukkan bahwa baja dengan plastisitas yang baik sering kali rusak karena pembebanan dinamis berulang dari tegangan utama dalam kasus kegagalan kelelahan.

Suplemen pada Perlakuan Efek Stres Rata-rata:

"Jika ada kurva S-N di bawah nilai R yang berbeda, metode interpolasi umumnya digunakan untuk menentukan kurva S-N di bawah nilai R yang tidak diketahui."

Ini hanya satu metode, yang berguna ketika ada beberapa tegangan yang harus diperiksa. Namun, metode ini bisa jadi tidak praktis apabila hanya memeriksa satu masa pakai.

Metode lainnya adalah menentukan setengah amplitudo tegangan ekuivalen di bawah kondisi R = -1, dan kemudian menerapkan kurva S-N secara langsung.

Ketika terdapat tegangan rata-rata, kurva S-N tidak dapat digunakan secara langsung. Sebagai gantinya, gunakan KURVA GOODMAN atau KURVA GOODMAN yang dimodifikasi.