Pernahkah Anda bertanya-tanya mengapa beberapa bahan mudah melengkung sementara yang lain tetap kaku? Blog ini menyelami dunia modulus elastisitas dan kekakuan yang menarik, mengungkap peran penting mereka dalam bidang teknik. Pada akhirnya, Anda akan memahami bagaimana sifat-sifat ini memengaruhi kekuatan dan fleksibilitas material sehari-hari.
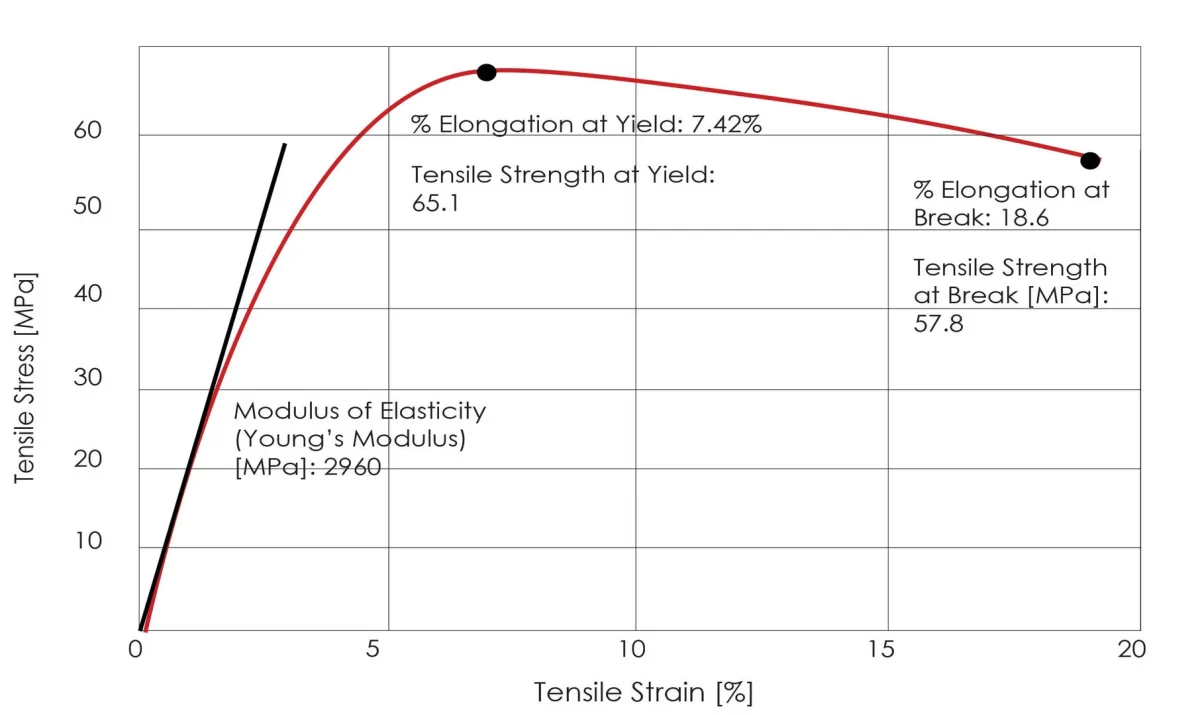
Modulus Elastisitas: Rasio tegangan normal terhadap regangan normal yang sesuai pada tahap deformasi elastis suatu bahan.
Pada tahap deformasi elastis, tegangan dan regangan suatu material adalah proporsional, sesuai dengan Hukum Hooke, dan koefisien proporsionalitas disebut sebagai modulus elastisitas.
Istilah "modulus elastisitas" adalah deskripsi umum dari elastisitas suatu bahan. Istilah ini mencakup beberapa modulus tertentu, termasuk modulus Young, modulus geser, dan modulus curah, di antaranya.
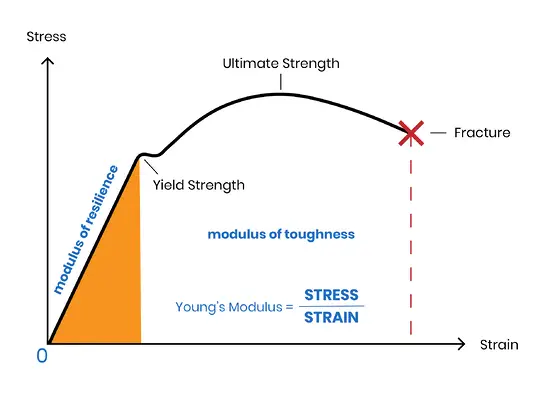
Oleh karena itu, "modulus elastisitas" dan "modulus curah" adalah istilah yang inklusif.
Ketika gaya eksternal (dikenal sebagai "tegangan") diterapkan pada elastomer, elastomer akan berubah bentuk (dikenal sebagai "regangan"). Modulus elastisitas didefinisikan sebagai rasio tegangan terhadap regangan.
Sebagai contoh:
Regangan Linier:
Ketika gaya tarik F diterapkan pada batang tipis, tegangan linier dihitung sebagai gaya tarik dibagi dengan luas penampang S batang.
Regangan linier dihitung sebagai perpanjangan batang (dL) dibagi dengan panjang aslinya (L).
Tegangan linier dibagi dengan regangan linier sama dengan modulus Young, E = (F/S) / (dL/L).
Regangan Geser:
Ketika gaya lateral (biasanya gaya gesekan) f diterapkan pada elastomer, elastomer berubah dari bentuk persegi menjadi bentuk berlian.
Sudut deformasi ini dikenal sebagai "regangan geser," dan gaya yang sesuai dibagi dengan area tegangan disebut "tegangan geser."
Tegangan geser dibagi dengan regangan geser sama dengan modulus geser, G = (f / S) / a.
Ketegangan Volume:
Ketika tekanan keseluruhan P diterapkan pada elastomer, ini dikenal sebagai "tekanan volume."
Pengurangan volume elastomer (-dV) dibagi dengan volume aslinya (V) disebut "regangan volume."
Tegangan volume dibagi dengan regangan volume sama dengan modulus curah, K = P / (-dV/V).
Secara umum, bila tidak ada kebingungan, modulus elastisitas bahan logam mengacu pada modulus Young, yang juga dikenal sebagai modulus elastisitas positif.
Satuan: E (modulus elastisitas) diukur dalam GPa.
Modulus elastisitas adalah parameter performa yang sangat penting dari material teknik.
Dari sudut pandang makro, ini mengukur kemampuan objek untuk menahan deformasi elastis, sementara dari sudut pandang mikro, ini mencerminkan kekuatan ikatan antara atom, ion, atau molekul.
Faktor-faktor yang memengaruhi kekuatan ikatan juga dapat memengaruhi modulus elastisitas suatu bahan, seperti mode ikatan, struktur kristal, komposisi kimia, struktur mikro, temperatur, dan lain-lain.
Modulus Young dari bahan logam dapat berfluktuasi lebih dari 5% karena komposisi paduan yang berbeda, status perlakuan panas, dan deformasi plastik dingin.
Namun, secara umum, modulus elastisitas bahan logam adalah indeks properti mekanis yang tidak sensitif terhadap struktur.
Paduan, perlakuan panas (struktur serat), dan deformasi plastis dingin memiliki efek terbatas pada modulus elastisitas, dan faktor eksternal seperti suhu dan laju pembebanan memiliki dampak yang dapat diabaikan.
Oleh karena itu, dalam aplikasi rekayasa umum, modulus elastisitas dianggap sebagai konstanta.
Satuan: GPa (gigapascal) untuk modulus elastisitas.
Modulus Elastisitas adalah ukuran ketahanan material terhadap deformasi elastis.
Semakin tinggi nilainya, semakin besar tegangan yang diperlukan untuk menghasilkan sejumlah deformasi elastis, yang berarti bahwa bahan tersebut lebih kaku dan mengalami lebih sedikit deformasi elastis di bawah tegangan yang diberikan.
Modulus Elastisitas, diwakili oleh E, adalah ukuran jumlah tegangan yang diperlukan bagi suatu bahan untuk mengalami deformasi elastisitas satuan di bawah gaya eksternal.
Ini mewakili kemampuan material untuk menahan deformasi elastis dan dapat dibandingkan dengan kekakuan musim semi.
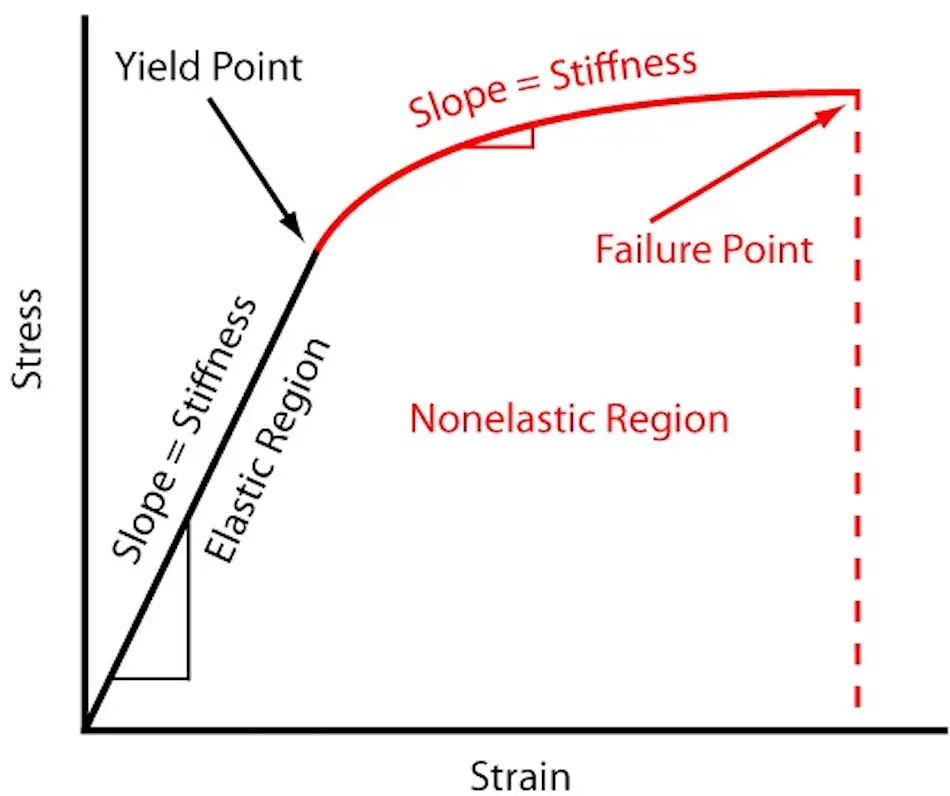
Kekakuan" mengacu pada kemampuan struktur atau komponen untuk menahan deformasi elastis. Hal ini ditentukan oleh gaya atau momen yang diperlukan untuk menghasilkan satu unit regangan.
Dari segi kekakuan rotasi, ini diwakili oleh "k" dan dapat dihitung sebagai "k = M/θ", di mana "M" adalah torsi yang diterapkan dan "θ" adalah sudut rotasi.
Kekakuan lainnya termasuk:
Metode penghitungan kekakuan dapat dibagi menjadi dua pendekatan: teori perpindahan kecil dan teori perpindahan besar.
Teori perpindahan besar memperhitungkan deformasi struktur setelah tegangan dan membentuk persamaan keseimbangan yang sesuai, memberikan hasil yang akurat tetapi dengan proses perhitungan yang lebih kompleks.
Sebaliknya, teori perpindahan kecil mengasumsikan bahwa struktur tidak terdeformasi secara signifikan, sehingga gaya internal dapat diperoleh dari beban eksternal dan kemudian digunakan untuk menghitung deformasi.
Pendekatan ini secara luas digunakan dalam sebagian besar aplikasi desain mekanis, karena jauh lebih sederhana untuk dipecahkan.
Sebagai contoh, dalam perhitungan deformasi tekukan balok, teori perpindahan kecil sering digunakan karena deformasi yang sebenarnya sangat kecil.
Teori ini melibatkan pengabaian turunan pertama defleksi dalam rumus kelengkungan dan menggunakan turunan kedua defleksi untuk memperkirakan kelengkungan sumbu balok, yang membantu menyederhanakan proses solusi dengan melinearisasi persamaan diferensial.
Ketika beberapa beban bekerja secara bersamaan, deformasi lentur yang disebabkan oleh masing-masing beban dapat dihitung secara terpisah dan kemudian digabungkan.
Resistensi terhadap deformasi di bawah beban statis dikenal sebagai kekakuan statis, sedangkan resistensi terhadap deformasi di bawah beban dinamis disebut sebagai kekakuan dinamis, yang berarti jumlah gaya dinamis yang diperlukan untuk satuan amplitudo.
Ketika gaya yang mengganggu berubah secara perlahan (yaitu, frekuensi gaya yang mengganggu jauh lebih kecil dari frekuensi alami struktur), kekakuan dinamik pada dasarnya sama dengan kekakuan statis.
Namun, jika gaya pengganggu berubah dengan cepat (yaitu, frekuensi gaya pengganggu jauh lebih besar daripada frekuensi alami struktur), deformasi struktur akan relatif kecil, dan dengan demikian kekakuan dinamik akan relatif besar.
Jika frekuensi gaya yang mengganggu mendekati frekuensi alami struktur, resonansi terjadi, dan kekakuan dinamik akan berada pada titik minimum, sehingga struktur paling mudah berubah bentuk, dengan deformasi dinamik yang mampu mencapai beberapa kali atau bahkan lebih dari sepuluh kali lipat deformasi beban statis.
Deformasi komponen yang berlebihan dapat berdampak pada pengoperasiannya.
Sebagai contoh, deformasi yang berlebihan pada poros roda gigi dapat memengaruhi penyambungan roda gigi, dan deformasi yang berlebihan pada alat mesin dapat mengurangi akurasi pemesinan.
Faktor-faktor yang mempengaruhi kekakuan termasuk modulus elastisitas bahan dan bentuk struktur. Mengubah bentuk struktur dapat berdampak signifikan pada kekakuan.
Perhitungan kekakuan adalah dasar dari teori getaran dan analisis stabilitas struktural. Ketika massa tetap konstan, kekakuan yang tinggi menghasilkan frekuensi natural yang tinggi.
Distribusi tegangan dalam struktur statis tak tentu berkaitan dengan rasio kekakuan setiap bagian.
Dalam mekanika fraktur analisis, faktor intensitas tegangan dari member yang retak dapat ditentukan berdasarkan fleksibilitasnya.
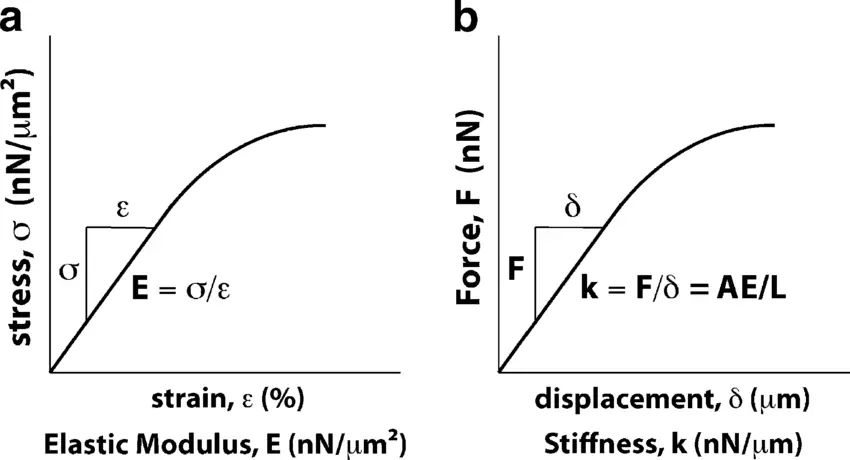
Kekakuan dan modulus elastisitas adalah konsep dasar dalam ilmu material, masing-masing menggambarkan aspek yang berbeda dari ketahanan material terhadap deformasi. Meskipun saling berkaitan, keduanya memiliki peran yang berbeda dalam analisis dan aplikasi material.
Modulus elastisitas, juga dikenal sebagai modulus Young, adalah ukuran spesifik dari kemampuan inheren material untuk menahan deformasi di bawah tekanan. Modulus elastisitas mengukur hubungan antara tegangan (gaya per satuan luas) dan regangan (deformasi proporsional) di daerah elastis linier dari kurva tegangan-regangan material. Modulus elastisitas adalah properti material dan tidak bergantung pada bentuk atau ukuran material. Hal ini dinyatakan dalam satuan tekanan, seperti Pascals (Pa).
Kekakuan, di sisi lain, adalah istilah yang lebih luas yang mengacu pada ketahanan struktur terhadap deformasi elastis di bawah beban yang diterapkan. Kekakuan bukan semata-mata properti material tetapi juga tergantung pada geometri dan kondisi batas struktur. Kekakuan biasanya dinyatakan sebagai gaya yang diperlukan untuk mencapai perpindahan satuan (misalnya, Newton per meter, N/m).
Kekakuan elemen struktur dapat diperoleh dari modulus elastisitas material dan geometri elemen. Sebagai contoh, kekakuan lentur (EI) dari sebuah balok adalah hasil kali antara modulus elastisitas (E) dan momen inersia (I) dari penampang balok. Demikian pula, kekakuan puntir (GI) adalah hasil kali dari modulus geser (G) dan momen inersia kutub (I).
Kekakuan sangat penting dalam desain teknik, terutama untuk komponen yang harus mempertahankan bentuknya di bawah beban, seperti spindel, rel pemandu, dan sekrup utama. Kekakuan juga penting untuk struktur yang membutuhkan kontrol deformasi yang ketat, seperti sayap pesawat terbang dan rakitan presisi tinggi.
Kekuatan adalah kemampuan material untuk menahan deformasi permanen dan fraktur di bawah kekuatan eksternal. Ini mencakup berbagai jenis kekuatan, termasuk kekuatan luluh, kekuatan tarik, kekuatan tekan, dan kekuatan lentur. Sifat-sifat ini sangat penting untuk menentukan kapasitas penahan beban dan daya tahan komponen mekanis.
Memahami perbedaan antara kekakuan dan modulus elastisitas sangat penting untuk mendesain dan menganalisis komponen dan struktur mekanis. Sementara modulus elastisitas memberikan ukuran ketahanan intrinsik material terhadap deformasi, kekakuan mempertimbangkan sifat material dan faktor geometris untuk menggambarkan ketahanan keseluruhan struktur terhadap deformasi. Kedua konsep tersebut merupakan bagian integral untuk memastikan kinerja dan keandalan desain teknik.
Sebagai pendiri MachineMFG, saya telah mendedikasikan lebih dari satu dekade karier saya untuk industri pengerjaan logam. Pengalaman saya yang luas telah memungkinkan saya untuk menjadi ahli di bidang fabrikasi lembaran logam, permesinan, teknik mesin, dan peralatan mesin untuk logam. Saya terus berpikir, membaca, dan menulis tentang subjek-subjek ini, terus berusaha untuk tetap menjadi yang terdepan di bidang saya. Biarkan pengetahuan dan keahlian saya menjadi aset bagi bisnis Anda.
ID 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO 
TR