Pernahkah Anda bertanya-tanya bagaimana mesin memilih motor yang sempurna? Artikel ini mengungkap proses menarik di balik pemilihan motor servo yang tepat untuk berbagai tugas mekanis. Selami untuk memahami perhitungan dan kriteria yang digunakan para insinyur untuk memastikan efisiensi dan presisi dalam mesin.
Diberikan:
Pilih motor servo dan roda gigi reduksi, skema komponen sebagai berikut:
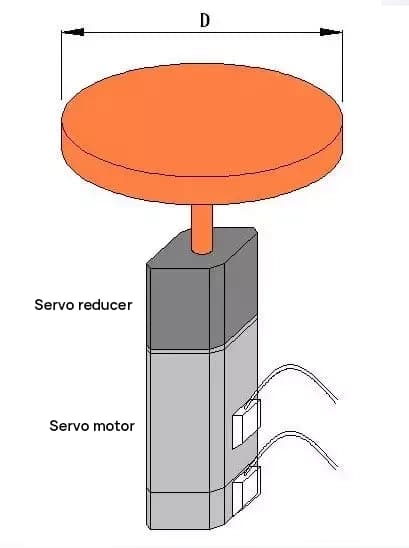
Menghitung momen inersia untuk rotasi cakram
JL = MD2/8 = 50 * 502 / 8 = 15625 [kg-cm2]
Dengan asumsi rasio reduksi roda gigi 1: R, inersia beban yang dipantulkan pada poros motor servo adalah 15625 / R2.
Menurut prinsip bahwa inersia beban harus kurang dari tiga kali inersia rotor JM dari motor,
jika motor 400W dipilih, JM = 0,277 [kg-cm2],
lalu: 15625 / R2 < 3*0.277, R2 > 18803, R > 137,
kecepatan output = 3000/137 = 22 [rpm],
yang tidak memenuhi persyaratan.
Jika motor 500W dipilih, JM = 8,17 [kg-cm2],
lalu: 15625 / R2 < 3*8.17, R2 > 637, R > 25,
kecepatan output = 2000/25 = 80 [rpm],
yang memenuhi persyaratan.
Jenis transmisi ini memiliki resistansi minimal, sehingga perhitungan torsi diabaikan.
Diberikan:
Mengabaikan berat setiap roda ban berjalan,
Berapa kebutuhan daya minimum motor untuk menggerakkan beban seperti itu?
Diagram skematik komponen adalah sebagai berikut:
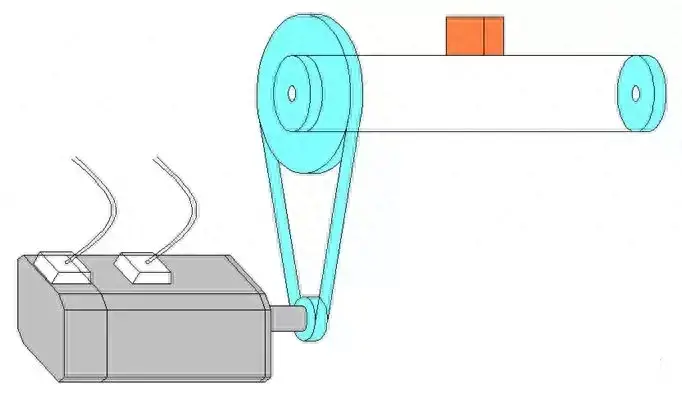
1. Menghitung inersia beban yang dipantulkan pada poros motor:
JL = M * D2 / 4 / R12
= 50 * 144 / 4 / 100
= 18 [kg-cm2]
Menurut prinsip bahwa inersia beban harus kurang dari tiga kali inersia rotor motor (JM):
JM > 6 [kg-cm2]
2. Menghitung torsi yang diperlukan untuk menggerakkan beban motor:
Torsi yang diperlukan untuk mengatasi gesekan:
Tf = M * g * µ * (D / 2) / R2 / R1
= 50 * 9.8 * 0.6 * 0.06 / 2 / 10
= 0,882 [N-m]
Torsi yang diperlukan untuk akselerasi:
Ta = M * a * (D / 2) / R2 / R1
= 50 * (30 / 60 / 0.2) * 0.06 / 2 / 10
= 0,375 [N-m]
Torsi pengenal motor servo harus lebih besar dari Tfdan torsi maksimum harus lebih besar dari Tf + Ta.
3. Menghitung kecepatan motor yang diperlukan:
N = v / (πD) * R1
= 30 / (3.14 * 0.12) * 10
= 796 [rpm]
Diberikan:
Pilih motor servo dengan daya minimum yang memenuhi persyaratan beban,
Diagram komponennya adalah sebagai berikut:
1. Perhitungan Inersia Beban yang Dikonversi ke Poros Motor
Inersia beban dari berat yang dikonversi ke poros motor
JW = M * (PB / 2π)²
= 200 * (2 / 6.28)²
= 20,29 [kg-cm²]
Kelambanan rotasi sekrup
JB = MB * DB² / 8
= 40 * 25 / 8
= 125 [kg-cm²]
Inersia beban total
JL = JW + JB = 145,29 [kg-cm²]
2. Perhitungan Kecepatan Motor
Kecepatan motor yang diperlukan
N = V / PB
= 30 / 0.02
= 1500 [rpm]
3. Perhitungan Torsi yang Dibutuhkan untuk Menggerakkan Beban Motor
Torsi yang diperlukan untuk mengatasi gesekan
Tf = M * g * µ * PB / 2π / η
= 200 * 9.8 * 0.2 * 0.02 / 2π / 0.9
= 1,387 [N-m]
Torsi yang dibutuhkan saat beban bertambah cepat
TA1 = M * a * PB / 2π / η
= 200 * (30 / 60 / 0.2) * 0.02 / 2π / 0.9
= 1,769 [N-m]
Torsi yang diperlukan saat sekrup berakselerasi
TA2 = JB * α / η
= JB * (N * 2π / 60 / t1) / η
= 0.0125 * (1500 * 6.28 / 60 / 0.2) / 0.9
= 10,903 [N-m]
Torsi total yang diperlukan untuk akselerasi
TA = TA1 + TA2 = 12,672 [N-m]
4. Pemilihan Motor Servo
Nilai torsi motor servo
T > Tf dan T > Trms
Torsi maksimum motor servo
Tmaks > Tf + TA
Akhirnya, motor ECMA-E31820ES yang dipilih.
Sebagai pendiri MachineMFG, saya telah mendedikasikan lebih dari satu dekade karier saya untuk industri pengerjaan logam. Pengalaman saya yang luas telah memungkinkan saya untuk menjadi ahli di bidang fabrikasi lembaran logam, permesinan, teknik mesin, dan peralatan mesin untuk logam. Saya terus berpikir, membaca, dan menulis tentang subjek-subjek ini, terus berusaha untuk tetap menjadi yang terdepan di bidang saya. Biarkan pengetahuan dan keahlian saya menjadi aset bagi bisnis Anda.
ID 
EN 
AR 
DE 
ES 
FR 
IT 
JA 
NL 
PT 
PT_BR 
RU 
KO 
TR