Vi siete mai chiesti come calcolare con precisione il margine di piegatura per i vostri progetti di fabbricazione di metalli? In questo post esploreremo l'affascinante mondo delle formule e dei calcoli di piegatura. In qualità di ingegnere meccanico esperto, vi guiderò attraverso i concetti chiave e fornirò spunti pratici per aiutarvi a padroneggiare questo aspetto cruciale della progettazione della lamiera. Preparatevi a immergervi e a svelare i segreti della creazione di curve precise ed efficienti nei vostri progetti!
La tolleranza di piegatura è un concetto critico nel campo della fabbricazione di lamiere, in particolare quando si lavora con operazioni di piegatura. Si riferisce alla lunghezza aggiuntiva di materiale necessaria per accogliere la piegatura nella lamiera. La comprensione e il calcolo accurato del margine di piegatura sono essenziali per garantire che le dimensioni finali del pezzo piegato siano conformi alle specifiche di progetto.
I calcoli accurati dei margini di piegatura sono fondamentali nel processo di fabbricazione. Quando una lamiera piatta viene piegata, il materiale all'esterno della curva si allunga, mentre quello all'interno si comprime. Senza tenere conto di questa deformazione, il prodotto finale non corrisponderebbe al progetto previsto, con conseguenti imprecisioni e potenziali guasti. La tolleranza di piegatura aiuta i fabbricanti a regolare le dimensioni del modello piatto, assicurando che il pezzo piegato soddisfi requisiti precisi.
Diversi parametri critici influenzano i calcoli dei margini di piegatura:
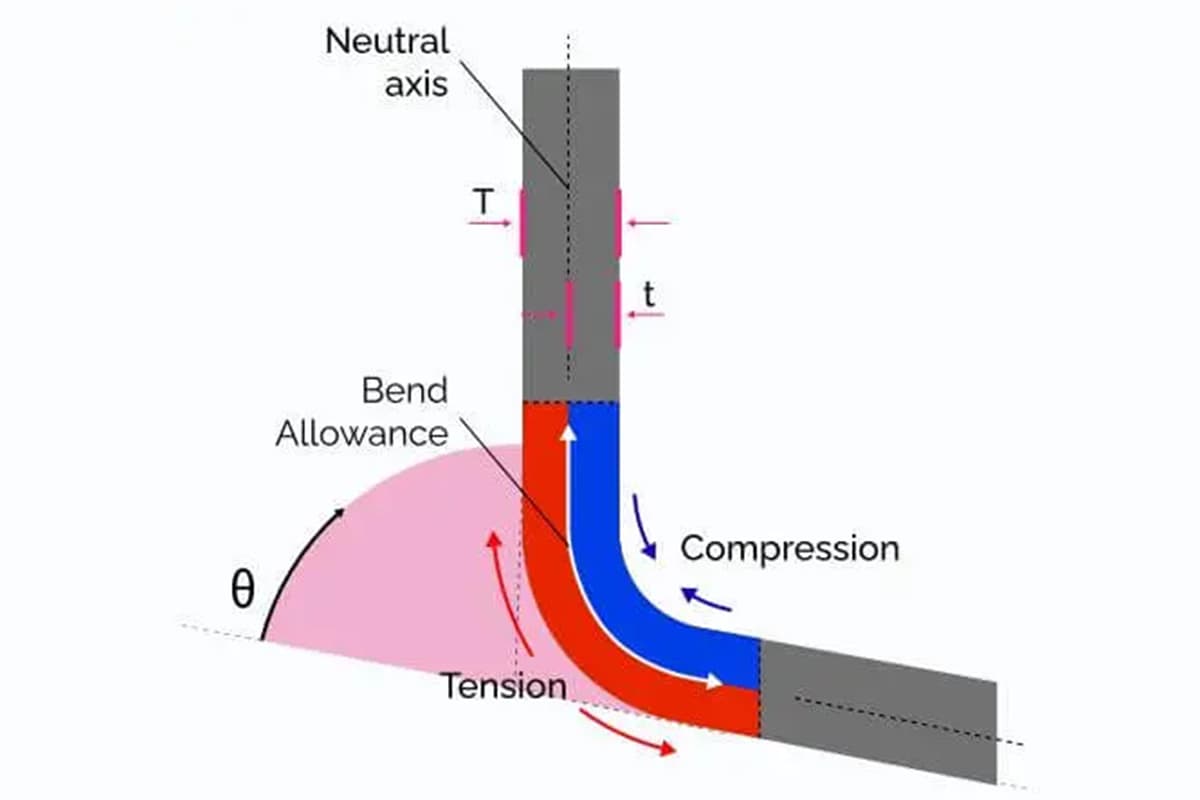
Il concetto di indennità di curvatura Quando una lamiera viene piegata, ha tre dimensioni: due esterne (L1 e L2) e una di spessore (T).
È importante notare che la somma di L1 e L2 è maggiore della lunghezza non piegata (L) e la differenza tra le due è nota come margine di flessione (K).
Di conseguenza, la lunghezza di una curva può essere calcolata come L = L1 + L2 - K.
Lettura correlata:
Come era la formula per indennità di curvatura creato? E come si calcola indennità di curvatura?
La tolleranza di piegatura dipende dal raggio interno formato. L'apertura dello stampo a V inferiore determina il raggio interno (R.I.) di un pezzo formato. Il raggio interno per l'acciaio dolce è 5/32 x l'apertura dello stampo a V inferiore (W) quando il raggio del punzone è inferiore a 5/32 x W.
Se I.R.< Spessore del materiale (t)
Se I.R. > 2 x spessore del materiale (t)
Dove A= (180 - angolo di curvatura incluso)
Se il raggio interno è uguale a t o 2t, o compreso tra t e 2t, il margine di curvatura viene calcolato interpolando i valori del margine di curvatura dalle due formule sopra citate.
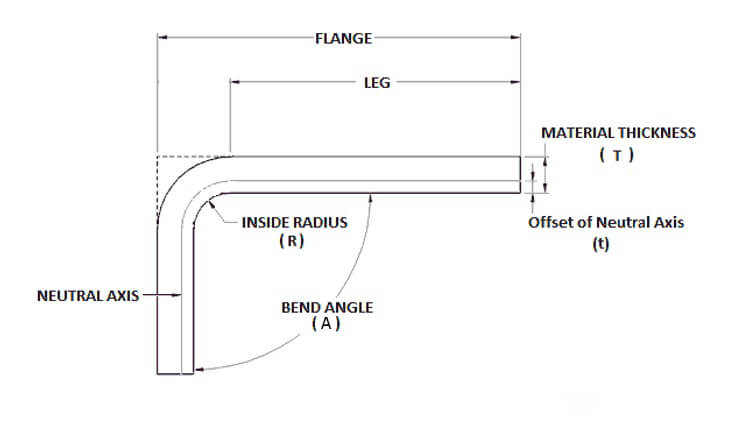
Inoltre, per calcolare questa indennità di flessione, è possibile utilizzare la seguente formula:
Questa formula tiene conto delle diverse geometrie e proprietà dei pezzi da formare.
Lo spessore del materiale (T), l'angolo di curvatura (A), l'interno raggio di curvatura (R) e il fattore K del materiale da piegare sono i fattori più critici in questo calcolo.
Come si evince dalla formula sopra riportata, il calcolo della tolleranza di flessione è un processo semplice.
È possibile determinare il margine di flessione sostituendo i valori sopra indicati nella formula.
Quando l'angolo di flessione è di 90°, la formula dell'indennità di flessione può essere semplificata come segue:
Nota: il fattore K per la maggior parte dei materiali e degli spessori standard è tipicamente compreso tra 0 e 0,5.
È possibile calcolare con precisione il valore del fattore K utilizzando la seguente formula Calcolatore del fattore K:
La formula del margine di piegatura (BA) è essenziale per calcolare la lunghezza del materiale necessaria per formare una curva. Questa formula generale è ampiamente applicabile a diversi materiali e metodi di piegatura:
Dove:
Il fattore K è fondamentale perché indica la posizione dell'asse neutro, che non cambia lunghezza durante la piegatura. In genere, il fattore K è compreso tra 0,3 e 0,5 e varia in base al tipo di materiale, allo spessore, al raggio e al metodo di piegatura.
I diversi materiali hanno proprietà uniche che richiedono aggiustamenti nei calcoli della tolleranza di piegatura. Questi aggiustamenti garantiscono l'accuratezza, in particolare per le curve a 90°:
Per i materiali più morbidi, come l'ottone o il rame, la tolleranza di piegatura viene calcolata come segue:
BA = (0,55 × T) + (1,57 × R
Questo aggiustamento tiene conto della duttilità del materiale e della sua minore resistenza alla deformazione.
Per il rame o l'ottone semiduri, l'acciaio dolce e l'alluminio, il margine di piegatura è pari a:
BA = (0,64 x T) + (1,57 × R)
Questi materiali hanno una durezza moderata e richiedono una tolleranza leggermente superiore rispetto ai materiali più morbidi.
Per i materiali più duri, come bronzo, rame duro, acciaio laminato a freddo e acciaio per molle, la formula è:
BA = (0,71 x T) + (1,57 × R)
Questi materiali sono più resistenti alla flessione e richiedono una tolleranza maggiore.
Per determinare la lunghezza totale in piano della parte in lamiera, il margine di piegatura viene sommato alle lunghezze delle parti piane:
Lunghezza piatta = Lunghezza gamba 1 + BA + Lunghezza gamba 2
Questo approccio garantisce che le dimensioni finali del pezzo siano precise dopo la piegatura.
Consideriamo una curva a 90° in una lastra di alluminio con uno spessore di 2 mm e un raggio di curvatura interno di 5 mm. Utilizzando la formula specifica del materiale per rame semiduro, ottone, acciaio dolce e alluminio:
BA = (0,64 × 2) + (1,57 × 5)
BA = 1,28 + 7,85=9,13
Se il pezzo ha due sezioni piane di 50 mm ciascuna, la lunghezza totale del piano sarà:
Lunghezza piatta = 50 + 9,13 + 50 = 109,13 mm
Oltre alla tolleranza di curvatura, la deduzione di curvatura (BD) e l'arretramento esterno (OSSB) sono importanti per ottenere misure accurate:
Deduzione di curva (BD) = OSSB - BA
Dove:
Queste formulazioni e considerazioni sono essenziali per calcolare con precisione i margini di piegatura, assicurando che le parti in lamiera siano prodotte con le dimensioni e l'adattamento corretti.
Il margine di piegatura è un fattore critico nel processo di piegatura della lamiera, in particolare per materiali come l'alluminio. Tiene conto dell'allungamento del materiale che si verifica durante la piegatura, garantendo dimensioni finali accurate. Qui discuteremo la formula specifica utilizzata per le lamiere di alluminio e la sua applicazione.
La tolleranza di flessione per una lastra di alluminio può essere calcolata con la seguente formula:
𝐿=𝐿1+𝐿2-1,6𝑇
Dove:
Il valore 1,6𝑇 è derivato empiricamente, cioè è stato stabilito attraverso la sperimentazione pratica e l'esperienza di produzione. Questo fattore tiene conto del comportamento del materiale durante la piegatura, garantendo l'accuratezza delle dimensioni finali.
È fondamentale notare che questa formula si applica specificamente a determinate condizioni:
Per determinare le dimensioni espanse della piastra di alluminio, procedere come segue:
Questo calcolo fornisce la lunghezza del modello piatto necessaria prima della piegatura, assicurando che il pezzo piegato finale abbia le dimensioni corrette.
Il calcolatore del margine di piegatura fornito di seguito semplifica il processo di calcolo del valore del margine di piegatura, che è fondamentale per una fabbricazione accurata della lamiera. Il margine di piegatura è la lunghezza dell'asse neutro tra le linee di piegatura, che aiuta a determinare le dimensioni corrette dello spezzone per un pezzo piegato.
L'angolo di piegatura, indicato come θ, è un parametro cruciale nella formula del coefficiente di piegatura. Rappresenta l'angolo di piegatura della lamiera. L'angolo di piegatura è tipicamente misurato in gradi, ma può essere convertito in radianti utilizzando la formula:
Il raggio interno, rappresentato come r, è il raggio della curva interna della piega. Questo raggio influenza direttamente la quantità di allungamento e compressione che si verifica nel materiale durante la piegatura. Un raggio interno più piccolo comporta una deformazione più significativa, che deve essere tenuta in considerazione nel calcolo della tolleranza di piegatura.
Lo spessore del materiale, indicato con T, è lo spessore della lamiera da piegare. I materiali più spessi subiscono un allungamento e una compressione più pronunciati, che influiscono sul margine di piegatura complessivo. La misurazione accurata dello spessore del materiale è essenziale per calcolare con precisione il margine di piegatura.
Il fattore K è un valore adimensionale che rappresenta la posizione dell'asse neutro rispetto allo spessore del materiale. L'asse neutro è la linea teorica all'interno del materiale che rimane invariata in lunghezza durante la flessione. Il fattore K varia in base alle proprietà del materiale e ai metodi di piegatura, in genere da 0,3 a 0,5 per la maggior parte dei materiali. La formula per la posizione dell'asse neutro è:
Posizione dell'asse neutro = K × T
L'asse neutro è la linea immaginaria all'interno del materiale che rimane invariata in lunghezza durante la piegatura. La comprensione della sua posizione è fondamentale per calcolare il corretto margine di piegatura.
Il margine di curvatura, rappresentato come BA, è la lunghezza dell'asse neutro necessaria per formare una curva. Si calcola con la formula:
Questa formula utilizza l'angolo di curvatura, il raggio interno, lo spessore del materiale e il fattore K per garantire calcoli accurati della tolleranza di curvatura.
La tabella delle tolleranze di piegatura è una risorsa essenziale per i professionisti che lavorano con la fabbricazione di lamiere. Fornisce un elenco completo di parametri chiave come lo spessore del materiale, il raggio di curvatura, l'angolo di curvatura, la tolleranza di curvatura e i valori di deduzione di curvatura per i materiali più comuni. Queste informazioni sono fondamentali per calcolare con precisione la lunghezza di sviluppo di un pezzo di lamiera dopo la piegatura.
Ulteriori letture:
| TV | Angolo | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Dimensione più corta |
| V4 | 90 | 0.9 | 1.4 | 2.8 | ||||||||||
| V4 | 120 | 0.7 | ||||||||||||
| V4 | 150 | 0.2 | ||||||||||||
| V6 | 90 | 1.5 | 1.7 | 2.15 | 4.5 | |||||||||
| V6 | 120 | 0.7 | 0.86 | 1 | ||||||||||
| V6 | 150 | 0.2 | 0.3 | 0.4 | ||||||||||
| V7 | 90 | 1.6 | 1.8 | 2.1 | 2.4 | 5 | ||||||||
| V7 | 120 | 0.8 | 0.9 | 1 | ||||||||||
| V7 | 150 | 0.3 | 0.3 | 0.3 | ||||||||||
| V8 | 90 | 1.6 | 1.9 | 2.2 | 2.5 | 5.5 | ||||||||
| V8 | 30 | 0.3 | 0.34 | 0.4 | 0.5 | |||||||||
| V8 | 45 | 0.6 | 0.7 | 0.8 | 1 | |||||||||
| V8 | 60 | 1 | 1.1 | 1.3 | 1.5 | |||||||||
| V8 | 120 | 0.8 | 0.9 | 1.1 | 1.3 | |||||||||
| V8 | 150 | 0.3 | 0.3 | 0.2 | 0.5 | |||||||||
| V10 | 90 | 2.7 | 3.2 | 7 | ||||||||||
| V10 | 120 | 1.3 | 1.6 | |||||||||||
| V10 | 150 | 0.5 | 0.5 | |||||||||||
| V12 | 90 | 2.8 | 3.65 | 4.5 | 8.5 | |||||||||
| V12 | 30 | 0.5 | 0.6 | 0.7 | ||||||||||
| V12 | 45 | 1 | 1.3 | 1.5 | ||||||||||
| V12 | 60 | 1.7 | 2 | 2.4 | ||||||||||
| V12 | 120 | 1.4 | 1.7 | 2 | ||||||||||
| V12 | 150 | 0.5 | 0.6 | 0.7 | ||||||||||
| V14 | 90 | 4.3 | 10 | |||||||||||
| V14 | 120 | 2.1 | ||||||||||||
| V14 | 150 | 0.7 | ||||||||||||
| V16 | 90 | 4.5 | 5 | 11 | ||||||||||
| V16 | 120 | 2.2 | ||||||||||||
| V16 | 150 | 0.8 | ||||||||||||
| V18 | 90 | 4.6 | 13 | |||||||||||
| V18 | 120 | 2.3 | ||||||||||||
| V18 | 150 | 0.8 | ||||||||||||
| V20 | 90 | 4.8 | 5.1 | 6.6 | 14 | |||||||||
| V20 | 120 | 2.3 | 3.3 | |||||||||||
| V20 | 150 | 0.8 | 1.1 | |||||||||||
| V25 | 90 | 5.7 | 6.4 | 7 | 17.5 | |||||||||
| V25 | 120 | 2.8 | 3.1 | 3.4 | ||||||||||
| V25 | 150 | 1 | 1 | 1.2 | ||||||||||
| V32 | 90 | 7.5 | 8.2 | 22 | ||||||||||
| V32 | 120 | 4 | ||||||||||||
| V32 | 150 | 1.4 | ||||||||||||
| V40 | 90 | 8.7 | 9.4 | 28 | ||||||||||
| V40 | 120 | 4.3 | 4.6 | |||||||||||
| V40 | 150 | 1.5 | 1.6 |
| TV | Angolo | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Dimensione più corta |
| V4 | 1.4 | 2.8 | ||||||||||||
| V6 | 1.6 | 4.5 | ||||||||||||
| V7 | 1.6 | 1.8 | 5 | |||||||||||
| V8 | 1.8 | 2.4 | 3.1 | 5.5 | ||||||||||
| V10 | 2.4 | 3.2 | 7 | |||||||||||
| V12 | 2.4 | 3.2 | 8.5 | |||||||||||
| V14 | 3.2 | 10 | ||||||||||||
| V16 | 3.2 | 4 | 4.8 | 11 | ||||||||||
| V18 | 4.8 | 13 | ||||||||||||
| V20 | 4.8 | 14 | ||||||||||||
| V25 | 4.8 | 5.4 | 6 | 17.5 | ||||||||||
| V32 | 6.3 | 6.9 | 22 |
| Angolo | 0.6 | 0.8 | 1 | 1.2 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | Dimensione più corta |
| 90 | 3.6 | 5.2 | 6.8 | 8.4 | 28 | ||||||||
| 120 | |||||||||||||
| 150 |
| MATERIALE | SPCC | SUS | Al （LY12） | SECC | ||||
|---|---|---|---|---|---|---|---|---|
| T | ΔT | ΔK | ΔT | ΔK | ΔT | ΔK | ΔT | ΔK |
| T=0.6 | 1.25 | 1.26 | ||||||
| T=0.8 | 0.18 | 1.42 | 0.15 | 1.45 | 0.09 | 1.51 | ||
| T=1.0 | 0.25 | 1.75 | 0.20 | 1.80 | 0.30 | 1.70 | 0.38 | 1.62 |
| T=1.2 | 0.45 | 1.95 | 0.25 | 2.15 | 0.50 | 1.90 | 0.43 | 1.97 |
| T=1.4 | 0.64 | 2.16 | ||||||
| T=1.5 | 0.64 | 2.36 | 0.50 | 2.50 | 0.70 | 2.30 | ||
| T=1.6 | 0.69 | 2.51 | ||||||
| T=1.8 | 0.65 | 3.00 | ||||||
| T=1.9 | 0.60 | 3.20 | ||||||
| T=2.0 | 0.65 | 3.35 | 0.50 | 3.50 | 0.97 | 3.03 | 0.81 | 3.19 |
| T=2.5 | 0.80 | 4.20 | 0.85 | 4.15 | 1.38 | 3.62 | ||
| T=3.0 | 1.00 | 5.00 | 5.20 | 1.40 | 4.60 | |||
| T=3.2 | 1.29 | 5.11 | ||||||
| T=4.0 | 1.20 | 6.80 | 1.00 | 7.00 | ||||
| T=5.0 | 2.20 | 7.80 | 2.20 | 7.80 | ||||
| T=6.0 | 2.20 | 9.80 | ||||||
Nota:
Una tabella di tolleranza di piegatura ben curata è uno strumento fondamentale nell'industria della fabbricazione della lamiera. Garantisce precisione ed efficienza nel processo di piegatura, consentendo di ottenere prodotti finiti di qualità superiore e più accurati. Comprendendo e utilizzando i valori forniti nella tabella, ingegneri e costruttori possono ottenere risultati ottimali nei loro progetti.
Nella lavorazione della lamiera, la precisione e l'accuratezza sono fondamentali per creare pezzi di alta qualità. Uno dei fattori chiave che giocano un ruolo significativo in questo processo è il fattore K. La comprensione del fattore K e della sua applicazione nei calcoli di piegatura è essenziale per i fabbricanti per produrre pezzi che soddisfino le specifiche esatte e funzionino in modo affidabile in vari settori.
Il fattore K è un valore adimensionale che rappresenta il rapporto tra la distanza dall'asse neutro e lo spessore del materiale. È fondamentale per un calcolo accurato del margine di curvatura, che determina la quantità di materiale necessaria per ottenere la curvatura desiderata. L'asse neutro è una linea immaginaria all'interno del materiale che non cambia di lunghezza durante la piegatura. Conoscendo il fattore K, i produttori possono prevedere il comportamento del materiale quando viene piegato, garantendo processi di produzione precisi ed efficienti.
Il fattore K viene calcolato con la formula:
Dove:
L'uso del fattore K nella formula del margine di piegatura aiuta a prevedere l'allungamento e la compressione del materiale durante la piegatura. La formula di piegatura è:
Per illustrare questo aspetto, facciamo un semplice esempio. Supponiamo di avere un pezzo di lamiera con uno spessore (T) di 2 mm, piegato con un angolo di 90 gradi (θ), con un raggio interno (r) di 5 mm e con un fattore K (K) di 0,4.
1. Convertire l'angolo di curvatura in radianti:
2. Applicare i valori alla formula del margine di piegatura:
Questo calcolo mostra che sono necessari circa 9,11 mm di materiale lungo l'asse neutro per ottenere la curvatura desiderata, dimostrando l'importanza di un fattore K accurato.
Il fattore K influisce direttamente sulla precisione dei calcoli delle quote di piegatura. Un fattore K preciso garantisce che le dimensioni finali del pezzo piegato corrispondano alle specifiche di progetto, riducendo lo spreco di materiale e la necessità di rilavorazioni. Questa precisione è fondamentale per i settori in cui le dimensioni esatte sono cruciali per l'assemblaggio e la funzionalità dei componenti.
I diversi materiali hanno proprietà meccaniche uniche, che si traducono in valori di fattore K diversi. Materiali più morbidi come l'alluminio hanno in genere un fattore K più basso, mentre materiali più duri come l'acciaio inox hanno un fattore K più alto. La comprensione di queste variazioni consente ai produttori di selezionare i valori del fattore K appropriati per i diversi materiali, garantendo calcoli accurati e processi di produzione efficienti.
Di seguito sono riportate le risposte ad alcune domande frequenti:
La formula della tolleranza di piegatura viene utilizzata per calcolare la lunghezza dell'asse neutro di una piegatura in lamiera, che è fondamentale per determinare la lunghezza corretta del modello piatto prima che il metallo venga piegato. Questo calcolo garantisce che le dimensioni finali del pezzo piegato corrispondano alle specifiche di progetto.
La formula tiene conto di diversi parametri chiave:
La formula generale per l'indennità di curvatura (BA) è:
Utilizzando questa formula, è possibile calcolare la lunghezza esatta del materiale necessario per formare una curva, assicurandosi che il materiale non si allunghi eccessivamente né si comprima troppo. Questo margine di piegatura calcolato viene poi aggiunto alle lunghezze delle gambe del pezzo per sviluppare un modello piatto accurato, essenziale per produrre pezzi con dimensioni precise.
La formula della tolleranza di piegatura è anche correlata alla deduzione di piegatura, che è la lunghezza che deve essere sottratta dalla lunghezza totale della lamiera per ottenere il modello piatto corretto. La deduzione di piega viene calcolata utilizzando il margine di piegatura e l'arretramento esterno, assicurando che le dimensioni finali del pezzo siano precise dopo la piegatura.
Ad esempio, se si sta piegando una lamiera di acciaio inox di 2 mm di spessore ad un angolo di 90° con un raggio di curvatura interno di 3 mm e un fattore K di 0,44, la tolleranza di piegatura può essere calcolata come segue:
Questa tolleranza di piegatura viene quindi utilizzata per garantire che il modello piatto sia sviluppato correttamente, ottenendo un pezzo che soddisfa le specifiche di progetto. In sintesi, la formula della tolleranza di piegatura è essenziale per un'accurata lavorazione della lamiera, garantendo che i pezzi finali siano prodotti con le dimensioni corrette.
Per calcolare il margine di piegatura della lamiera, è necessario determinare diversi parametri chiave: spessore del materiale (T), angolo di piegatura (θ), raggio interno (r) e fattore K (K). Il margine di piegatura (BA) si calcola con la formula:
Ecco un procedimento passo dopo passo:
Utilizzando questa formula, per gli stessi parametri:
Seguendo questi passaggi e utilizzando la formula appropriata, è possibile calcolare con precisione il margine di piegatura per le parti in lamiera, garantendo una lavorazione precisa.
Il fattore K è importante nella formula della tolleranza di piegatura per diversi motivi, ognuno dei quali ne evidenzia l'importanza nella fabbricazione di lamiere di precisione. In primo luogo, rappresenta il rapporto tra l'asse neutro e lo spessore del materiale. Durante la piegatura, l'asse neutro si sposta dalla sua posizione originale a 50% dello spessore del materiale verso la superficie interna della piega. Questo spostamento è fondamentale perché determina la quantità di allungamento che si verifica nel materiale. Il fattore K aiuta a calcolare questa nuova posizione, essenziale per un calcolo accurato della piegatura.
In secondo luogo, il fattore K è fondamentale per calcolare il margine di piegatura, ovvero la lunghezza della fibra neutra dall'inizio alla fine dell'arco generato dalla piegatura. Questo calcolo è necessario per determinare le dimensioni piane della lamiera necessarie per ottenere la forma di piegatura desiderata. Il margine di piegatura è direttamente influenzato dal fattore K, che tiene conto dell'allungamento del materiale durante il processo di piegatura.
Inoltre, l'uso del fattore K consente di calcolare con precisione le deduzioni di piegatura, gli arretramenti esterni e il layout piatto complessivo del pezzo. Questa precisione è fondamentale perché garantisce che le dimensioni finali del pezzo piegato corrispondano alle specifiche di progetto, evitando gli errori che potrebbero derivare dall'utilizzo di valori generici o imprecisi del fattore K.
Il fattore K varia in base a diversi parametri, tra cui il tipo di materiale, lo spessore, il metodo di formatura, gli utensili e l'angolo di piegatura. Questa variabilità significa che il fattore K deve essere adattato alle condizioni specifiche del processo di piegatura. Considerando questi fattori, il fattore K aiuta a personalizzare la formula di compensazione della piegatura per ottenere risultati più accurati.
Infine, un valore corretto del fattore K è essenziale per evitare errori nelle dimensioni finali della lamiera piegata. Valori errati del fattore K possono portare a imprecisioni nelle tolleranze di piegatura, con il risultato di pezzi non conformi alle specifiche richieste. Pertanto, determinare e utilizzare con precisione il fattore K è fondamentale per produrre componenti di alta qualità.
In sintesi, il fattore K è importante perché consente di calcolare con precisione i margini di piegatura, tiene conto dello spostamento dell'asse neutro e considera i parametri specifici del materiale e del processo, tutti elementi essenziali per ottenere risultati precisi e affidabili nella piegatura della lamiera.
La formula della tolleranza di piegatura nella piegatura della lamiera include comunemente diverse variabili chiave:
Il margine di curvatura (BA) può essere calcolato con la formula:
o
dove (0,017453) è (π/180) e (0,0078) è (π /180) x K) - fattore.
Queste variabili sono essenziali per determinare con precisione la tolleranza di piegatura, fondamentale per una precisa lavorazione della lamiera.
Sì, la formula della tolleranza di piegatura può variare in modo significativo in base al tipo di materiale e ad altri fattori quali lo spessore del materiale, l'angolo di piegatura e il processo di piegatura specifico.
Il fattore K, un componente critico della formula del coefficiente di piegatura, rappresenta lo spostamento dell'asse neutro teorico durante la flessione e varia a seconda del materiale. Ad esempio, l'acciaio dolce laminato a freddo utilizza in genere un fattore K di circa 0,446, mentre altri materiali come l'acciaio inossidabile e l'alluminio hanno fattori K diversi a causa delle loro proprietà uniche e dei loro comportamenti di flessione.
La formula del margine di curvatura incorpora anche lo spessore del materiale e l'angolo di curvatura, che possono variare a seconda dei materiali. Una forma generale della formula del margine di curvatura è:
dove:
I diversi materiali hanno proprietà diverse, come l'elasticità, la resistenza alla trazione e la direzione delle venature, che influenzano il loro comportamento a flessione. Ad esempio, l'alluminio si piega più facilmente dell'acciaio, il che richiede un adeguamento del calcolo del margine di piegatura. Inoltre, la piegatura di un metallo lungo la direzione della grana può richiedere una forza maggiore e una tolleranza di piegatura diversa rispetto alla piegatura trasversale.
È necessario considerare anche la tendenza del materiale a tornare indietro dopo la flessione, nota come ritorno elastico. Questo comporta una leggera sovracurvatura del materiale per tenere conto del recupero elastico, influenzato dal tipo di materiale e dalle sue proprietà.
In sintesi, la formula della tolleranza di piegatura deve essere adattata al materiale specifico utilizzato, tenendo conto delle sue proprietà uniche, dello spessore e del processo di piegatura.
In qualità di fondatore di MachineMFG, ho dedicato oltre un decennio della mia carriera al settore della lavorazione dei metalli. La mia vasta esperienza mi ha permesso di diventare un esperto nei campi della fabbricazione di lamiere, della lavorazione, dell'ingegneria meccanica e delle macchine utensili per metalli. Penso, leggo e scrivo costantemente su questi argomenti, cercando di essere sempre all'avanguardia nel mio campo. Lasciate che le mie conoscenze e la mia esperienza siano una risorsa per la vostra azienda.
IT 
EN 
AR 
DE 
ES 
FR 
ID 
JA 
NL 
PT 
PT_BR 
RU 
KO 
TR