Come fanno gli ingegneri a garantire la resistenza e la durata delle travi sotto vari carichi? Questo articolo approfondisce i principi della sollecitazione di taglio a flessione e le condizioni necessarie per mantenere la resistenza delle travi. Tratta della distribuzione delle sollecitazioni in diverse sezioni di travi - rettangolari, circolari, a I e anulari a parete sottile - e suggerisce anche modi per migliorare le prestazioni delle travi attraverso una migliore progettazione e l'uso dei materiali. Imparate a capire come interagiscono le sollecitazioni di taglio e di flessione e scoprite i consigli pratici per ottimizzare la costruzione e l'applicazione delle travi.
Sulla sezione trasversale di una trave sottoposta a forza trasversale si verificano sia il momento flettente che la forza di taglio, con conseguente sollecitazione normale e di taglio sulla sezione trasversale. La sollecitazione di taglio a flessione di diverse sezioni di travi comuni sarà discussa in seguito.
Un piccolo segmento di lunghezza dx viene tagliato dalla trave sottoposta a flessione per forza trasversale. La trave è priva di carico e le forze di taglio su entrambi i lati del segmento sono uguali ma in direzioni opposte. Il momento flettente sulla sezione destra è maggiore di quello sulla sezione sinistra, con conseguente diverso sforzo normale sulle due sezioni.
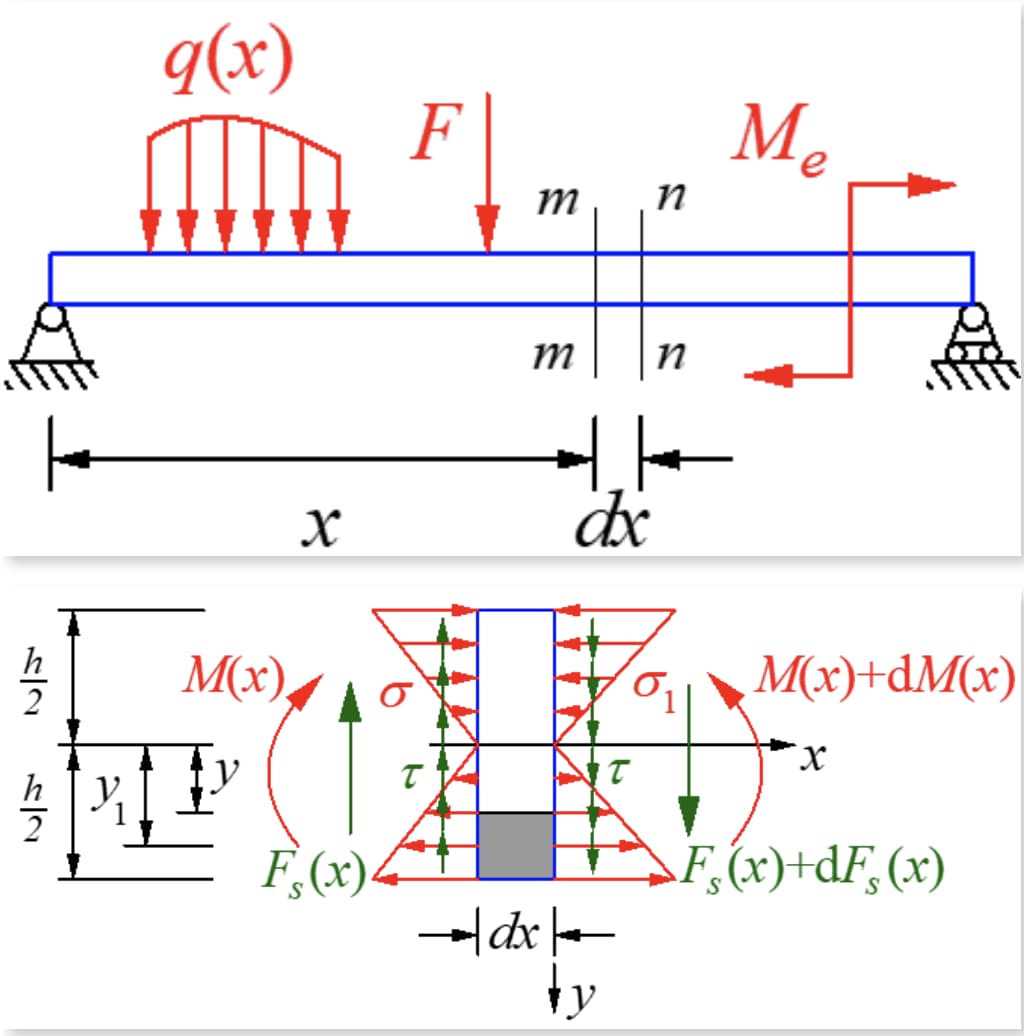
Per una sezione rettangolare stretta, la sollecitazione di taglio è tangente al confine su entrambi i lati della trave a causa dell'assenza di sollecitazioni di taglio sul lato. Ciò significa che, poiché la trave è piegata simmetricamente e parallela al confine, la sollecitazione di taglio sull'asse y dell'asse di simmetria deve essere nella direzione y e cambia poco lungo la direzione della larghezza.
Pertanto, si fanno le seguenti ipotesi sulla legge di distribuzione dello sforzo di taglio sulla sezione trasversale:
Quando il rapporto altezza/larghezza della sezione è maggiore di 2, la soluzione basata sull'ipotesi di cui sopra è sufficientemente accurata rispetto alla soluzione esatta della teoria elastica.
Secondo il teorema della reciprocità delle sollecitazioni di taglio, sulla sezione longitudinale perpendicolare alla sezione trasversale dovrebbe esserci una sollecitazione di taglio pari alla dimensione della sezione trasversale. Tagliare un micro segmento lungo il piano longitudinale con l'asse del momento neutro lontano da y e prendere il micro elemento sul lato inferiore del piano longitudinale. Le forze sono quelle mostrate nella figura seguente.
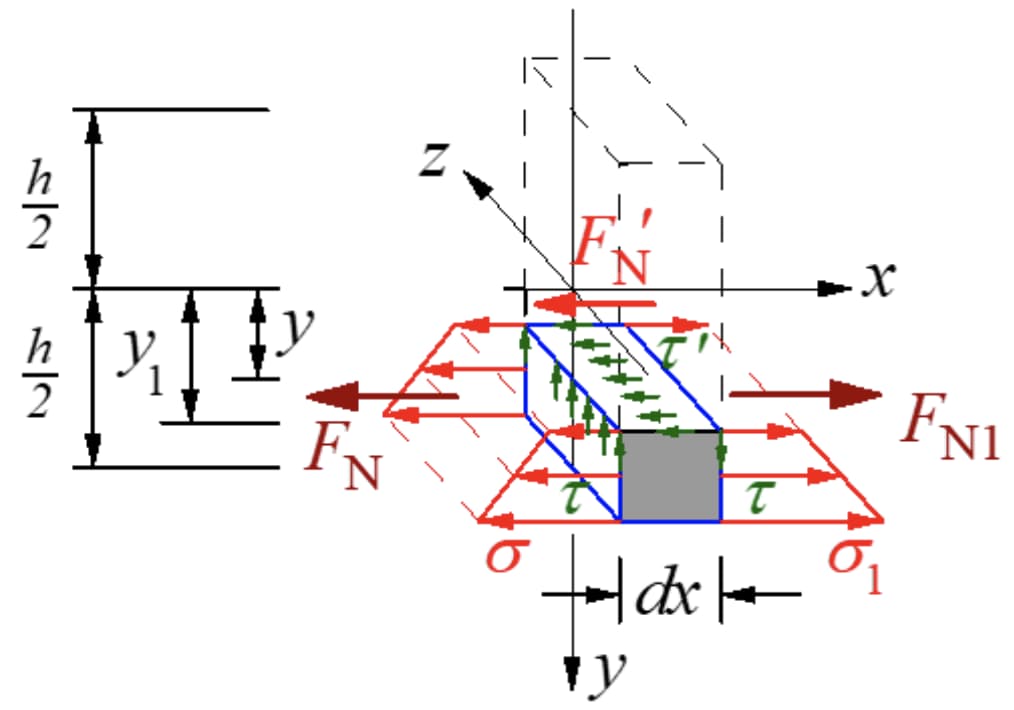
La forza risultante dello sforzo normale sulla sezione sinistra è:
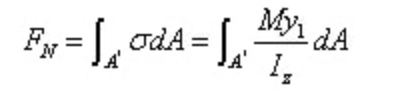
La forza risultante dello sforzo normale sulla sezione di destra è: - La forza risultante dello sforzo normale sulla sezione di destra è
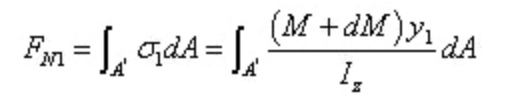
È evidente che le due risultanti sono di dimensioni diverse. Per mantenere l'equilibrio del microsegmento, sulla sezione longitudinale deve essere presente una forza lungo la direzione assiale. Questa forza è il risultato dello sforzo di taglio, a conferma della presenza di uno sforzo di taglio sulla sezione longitudinale.
Poiché dx è una quantità piccola, la sollecitazione di taglio sul piano longitudinale deve essere distribuita in modo uniforme：.
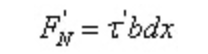
Secondo le condizioni di equilibrio
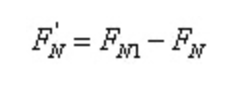
Cioè,
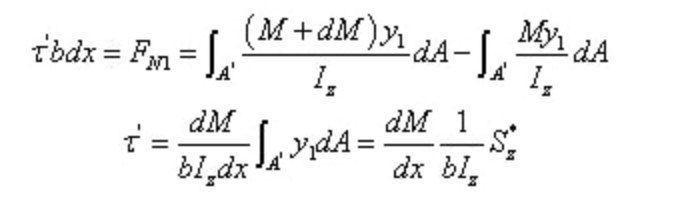
Tra,
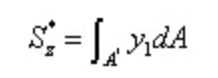
Dal teorema reciproco della sollecitazione di taglio e dalla relazione differenziale tra forza di taglio e momento flettente:
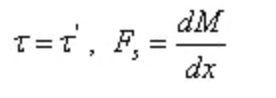
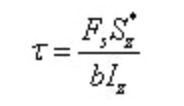
Di cui:
Tra,
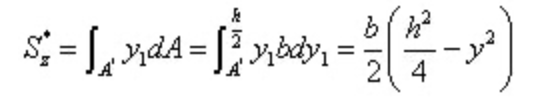
Sostituire nella formula di calcolo della sollecitazione di taglio
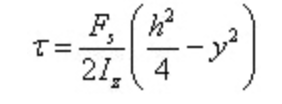
La sollecitazione di taglio è distribuita a parabola lungo l'altezza della sezione.
Quando y=0, si ha la massima sollecitazione di taglio sulla sezione in corrispondenza dell'asse neutro
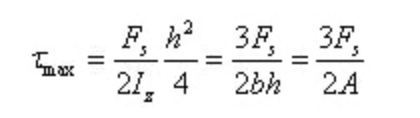
La deformazione angolare è
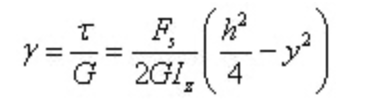
Si può notare che anche la deformazione angolare è distribuita a parabola lungo l'altezza della sezione.
A questo punto, la forma di deformazione della sezione trasversale quando la forza trasversale si piega è mostrata nella figura seguente, che verifica che la deformazione a flessione della forza trasversale non soddisfa l'ipotesi di piano.
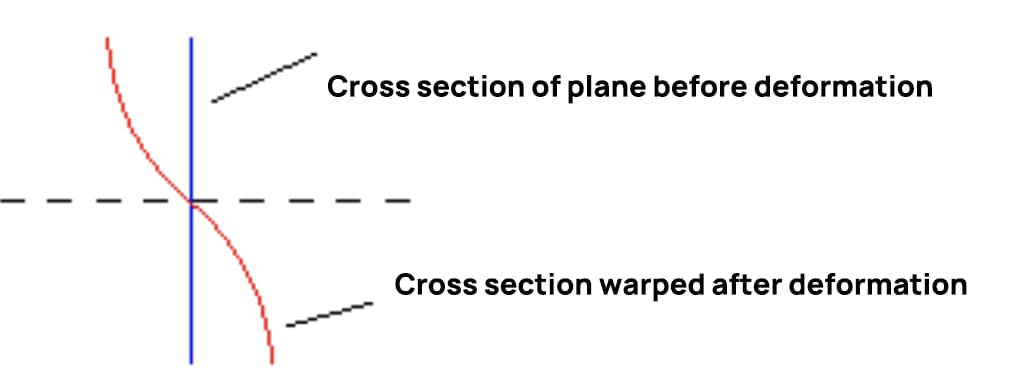
Quando la forza di taglio rimane costante, la sollecitazione di taglio sulle sezioni trasversali consecutive è uguale e anche il grado di deformazione è uguale. La lunghezza delle fibre longitudinali non cambia a causa dell'orditura della sezione, per cui non si genera uno sforzo normale aggiuntivo. Se la forza di taglio cambia con la posizione della sezione, il grado di deformazione su due sezioni consecutive sarà diverso, con conseguente aumento dello sforzo normale sulla sezione.
Per le sezioni simmetriche di altra forma, la soluzione approssimativa della sollecitazione di taglio può essere derivata con il metodo sopra descritto.
Per una sezione rettangolare, nella formula di calcolo delle sollecitazioni, la larghezza della sezione (b) è costante e il momento statico della metà dell'area della sezione trasversale su un lato dell'asse neutro rispetto all'asse neutro è il più grande. Di conseguenza, la sollecitazione di taglio in ogni punto dell'asse neutro è la più elevata.
Per le sezioni simmetriche di altre forme, la massima sollecitazione di taglio sulla sezione trasversale è tipicamente localizzata in vari punti dell'asse neutro, con l'eccezione delle sezioni con larghezza significativamente aumentata sull'asse neutro (come le sezioni trasversali) o di alcune sezioni con larghezza variabile (come le sezioni a triangolo isoscele).
Pertanto, per le travi a forma di I, anulari e a sezione circolare, la massima sollecitazione di taglio in ogni punto dell'asse neutro sarà discussa principalmente di seguito.
La sollecitazione di taglio in ogni punto del bordo di una sezione circolare è tangente alla circonferenza, secondo il teorema reciproco della sollecitazione di taglio. In ciascun punto dell'asse di simmetria, la sollecitazione di taglio deve essere in direzione y. Si può supporre che la distribuzione delle sollecitazioni di taglio converga in un punto dell'asse di simmetria per ogni punto della larghezza y rispetto all'asse neutro e che le componenti delle sollecitazioni di taglio lungo la direzione Y in ogni punto della larghezza siano uguali.
La massima sollecitazione di taglio della sezione circolare si trova ancora sull'asse neutro e la sua direzione è parallela alla forza esterna, con lo stesso valore in ogni punto dell'asse neutro.
La massima sollecitazione di taglio è
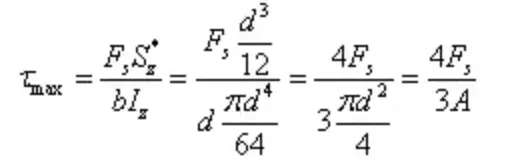
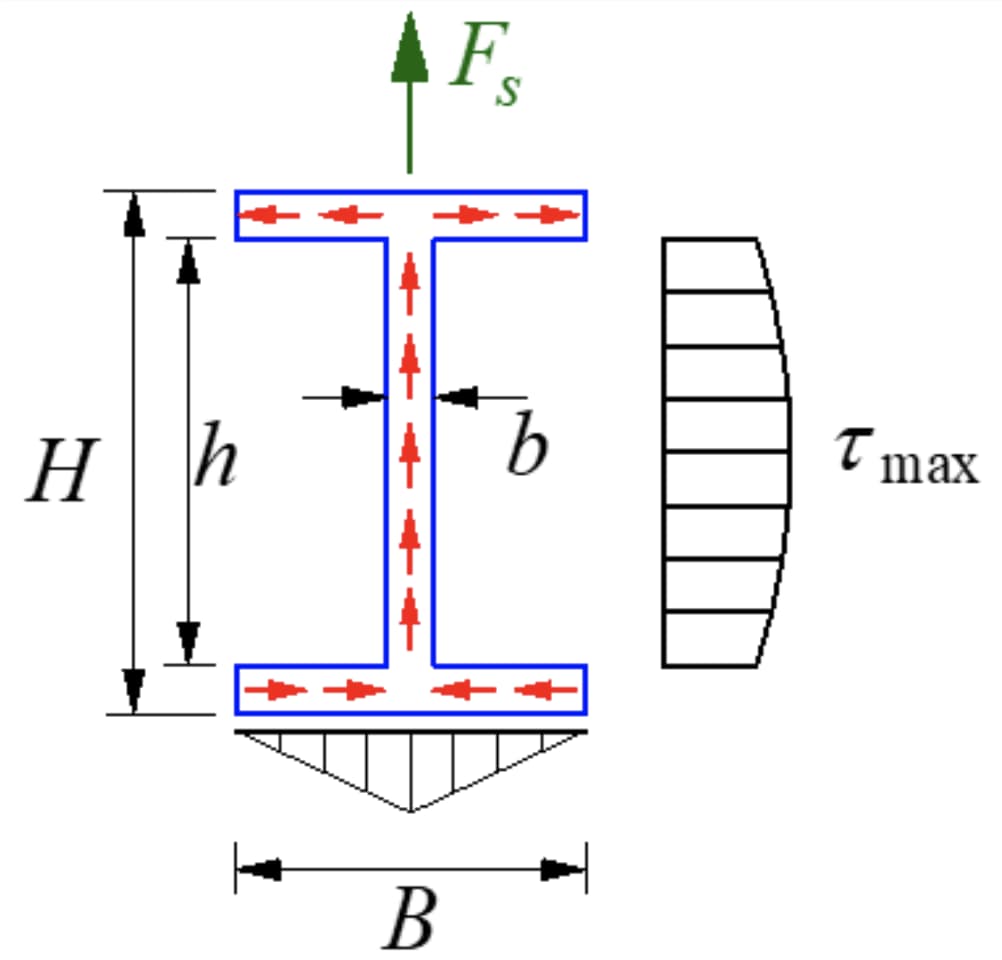
La sezione a I è una sezione aperta a parete sottile con una distribuzione delle sollecitazioni come mostrato in figura. L'entità della sollecitazione di taglio lungo lo spessore della parete è uguale, nota come flusso di sollecitazione di taglio, che scorre nella direzione del taglio.
La componente della sollecitazione di taglio parallela all'asse y sulla flangia è secondaria e trascurabile, mentre l'attenzione si concentra sulla componente parallela al lato lungo della flangia. La sollecitazione di taglio sull'anima ha una distribuzione parabolica, la cui dimensione è mostrata nella figura.
La massima sollecitazione di taglio si trova in corrispondenza dell'asse neutro.
In caso di Acciaio a forma di I, la massima sollecitazione di taglio:
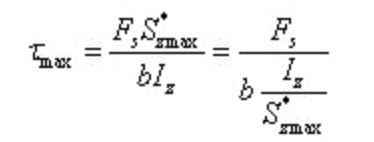
Dove b è lo spessore del nastro e Iz/s*zmax si può ottenere facendo riferimento alla tabella dei profili in acciaio.
Se si tratta di una sezione a I composta da tre rettangoli lunghi e stretti, le sollecitazioni di taglio massime e minime sull'anima possono essere ottenute come segue:
Dalle due formule precedenti, si può notare che la larghezza dell'anima è molto più piccola della larghezza della flangia, quindi la massima sollecitazione di taglio sull'anima non è molto diversa dalla sollecitazione di taglio minima.
Pertanto, si può ritenere che la sollecitazione di taglio sull'anima sia distribuita in modo approssimativamente uniforme.
La sollecitazione di taglio risultante sull'anima rappresenta il 95-97% della forza di taglio totale e la forza di taglio sulla sezione trasversale è sostenuta principalmente dall'anima.
Poiché l'anima sopporta quasi tutta la forza di taglio sulla sezione e la sollecitazione di taglio sull'anima è quasi uniformemente distribuita, la sollecitazione di taglio massima può essere calcolata approssimativamente dividendo la forza di taglio per l'area della sezione trasversale del polo ventrale:
Allo stesso tempo, l'intera area di Trave a I La flangia è la più lontana dall'asse neutro e lo sforzo normale in ogni punto è relativamente grande, quindi la flangia sopporta la maggior parte del momento flettente della sezione.
Lo spessore della sezione anulare a parete sottile è d, il raggio medio dell'anello è r e lo spessore è di gran lunga inferiore al raggio medio, quindi si può ipotizzare che:
La sollecitazione di taglio sulla sezione trasversale è uguale lungo lo spessore della parete;
La direzione dello sforzo di taglio è tangente alla linea centrale della sezione e la direzione del flusso dello sforzo di taglio è lungo la direzione del taglio.
La massima sollecitazione di taglio si trova sull'asse neutro:
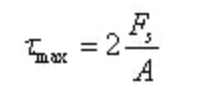
Dove A è l'area della sezione anulare.
Condizione di resistenza allo sforzo normale di flessione:
Per le sezioni assialsimmetriche neutre, la massima sollecitazione normale di trazione e la massima sollecitazione normale di compressione sono uguali.
I materiali plastici comunemente utilizzati e le loro condizioni di resistenza:
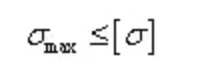
Per quanto riguarda la sezione con asse neutro asimmetrico, lo sforzo normale massimo di trazione e lo sforzo normale massimo di compressione non sono uguali.
Vengono comunemente utilizzati materiali fragili e le loro condizioni di resistenza:
La condizione di resistenza della sollecitazione di taglio a flessione è:
Lo sforzo normale di flessione è il principale fattore di controllo della trave.
Pertanto, la condizione di resistenza dello sforzo normale di flessione è spesso la base principale per la progettazione delle travi.
Dalla condizione di resistenza, per migliorare la capacità portante della trave, occorre considerare due aspetti:
Da un lato, la sollecitazione della trave deve essere ragionevolmente disposta per ridurre il momento flettente massimo;
D'altra parte, viene adottata una forma ragionevole della sezione per migliorare il coefficiente di flessione della sezione e sfruttare appieno le proprietà del materiale.
Migliorare le condizioni di sollecitazione della trave e cercare di ridurre il momento flettente massimo nella trave.
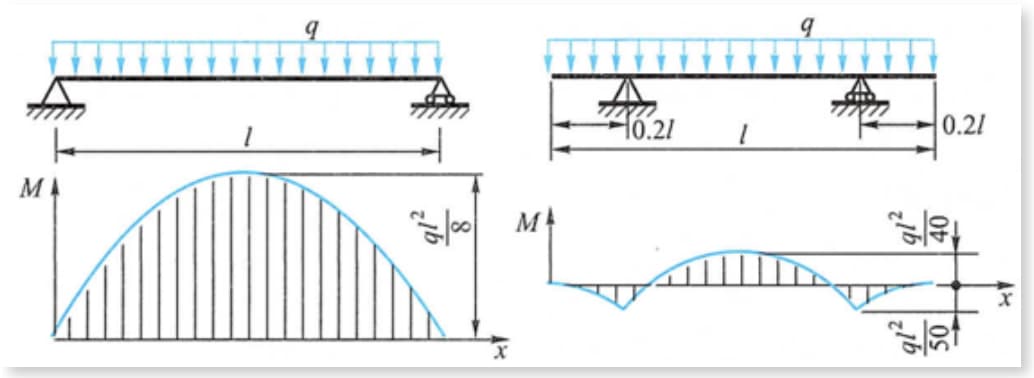
Come mostrato in figura, il momento flettente massimo sulla trave sotto carico uniforme si riduce notevolmente quando l'appoggio viene spostato verso l'interno per una certa distanza dalle posizioni di entrambe le estremità della trave.
Ad esempio, la trave e il contenitore cilindrico della gru a cavalletto, il cui punto di appoggio si sposta leggermente al centro, possono ottenere l'effetto di ridurre il momento flettente massimo.
Maggiore è il coefficiente di sezione flessionale, minore è la sollecitazione e maggiore è la capacità portante della trave.
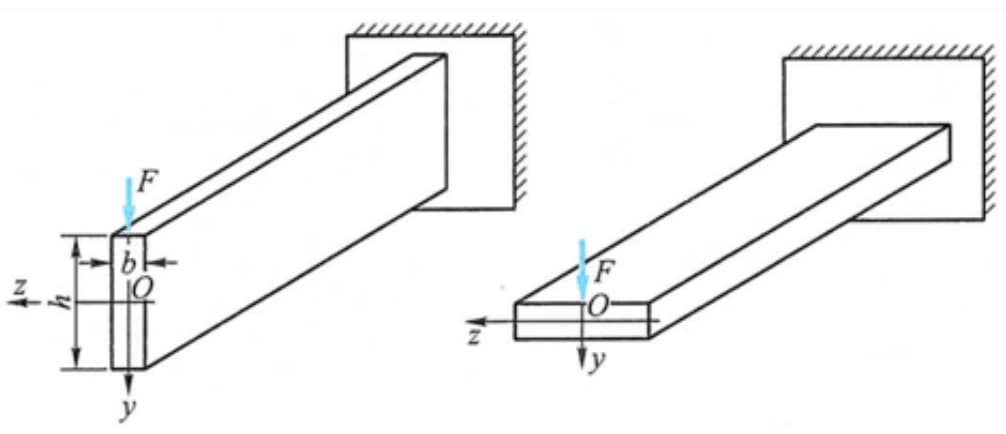
Ad esempio, quando la trave è caricata in direzione verticale, il coefficiente di flessione della sezione è maggiore quando la sezione è posizionata verticalmente, quindi è più ragionevole posizionarla verticalmente che orizzontalmente.
Migliorando il coefficiente di flessione della sezione, speriamo anche di utilizzare meno materiali per ottenere una migliore economia.
Pertanto, il rapporto tra il coefficiente di flessione della sezione e l'area della sezione è generalmente utilizzato per misurare la razionalità della progettazione della sezione.
A parità di sezione trasversale, la sezione rettangolare (altezza maggiore della larghezza) è più ragionevole della sezione circolare, mentre la sezione a forma di I o di scatola è più ragionevole della sezione rettangolare.
Pertanto, per sfruttare appieno i materiali, questi devono essere collocati il più lontano possibile dall'asse neutro.
Quando si discute della forma ragionevole della sezione, la proprietà meccaniche del materiale deve essere presa in considerazione.
I materiali con la stessa resistenza alla trazione e alla compressione (come l'acciaio a basso tenore di carbonio) dovrebbero adottare sezioni neutre asimmetriche, come quelle circolari, rettangolari, a I, scatolari, ecc.
In questo modo, la massima tensione di trazione e la massima tensione di compressione ai bordi superiore e inferiore della sezione possono essere uguali.
Per i materiali con resistenze disuguali a trazione e compressione (come la ghisa, il cemento, ecc.), si deve adottare la forma della sezione con l'asse neutro inclinato verso il lato di trazione.
Le travi discusse in precedenza hanno tutte la stessa sezione e il coefficiente di flessione è costante, ma in generale il momento flettente di ogni sezione della trave varia con la posizione della sezione stessa.
La progettazione della sezione di una trave rettilinea uguale deve essere effettuata in base al momento flettente massimo e la sua sollecitazione massima è vicina alla sollecitazione ammissibile.
Il momento flettente sulle altre sezioni è piccolo, quindi la sollecitazione è ridotta e il materiale non viene sfruttato appieno.
Per risparmiare materiali e ridurre il peso proprio, la dimensione della sezione può essere modificata in modo che il coefficiente della sezione di flessione cambi con il momento flettente.
Una sezione più grande viene utilizzata quando il momento flettente è maggiore, mentre una sezione più piccola viene utilizzata quando il momento flettente è minore.
Questo tipo di trave, la cui sezione cambia lungo l'asse, è chiamata trave a sezione variabile.
Se lo sforzo normale massimo su ogni sezione trasversale di una trave a sezione variabile è uguale e pari allo sforzo ammissibile, si parla di trave a resistenza uguale.
In qualità di fondatore di MachineMFG, ho dedicato oltre un decennio della mia carriera al settore della lavorazione dei metalli. La mia vasta esperienza mi ha permesso di diventare un esperto nei campi della fabbricazione di lamiere, della lavorazione, dell'ingegneria meccanica e delle macchine utensili per metalli. Penso, leggo e scrivo costantemente su questi argomenti, cercando di essere sempre all'avanguardia nel mio campo. Lasciate che le mie conoscenze e la mia esperienza siano una risorsa per la vostra azienda.
IT 
EN 
AR 
DE 
ES 
FR 
ID 
JA 
NL 
PT 
PT_BR 
RU 
KO 
TR