Come fa una trave in acciaio a resistere al peso di un ponte o alla pressione di una gru? Questo articolo approfondisce i calcoli della resistenza a flessione delle sezioni in acciaio, spiegando i concetti di fasi elastiche, elastoplastiche e plastiche. Comprendendo la resistenza e la rigidità delle diverse sezioni, i lettori impareranno a garantire la sicurezza e la stabilità delle strutture sotto vari carichi. Immergetevi per comprendere i principi fondamentali che mantengono le nostre costruzioni alte e resistenti.
1. Concetto:
Supporta carichi laterali come travi per solai, travi per gru, arcarecci, ponti, ecc.
2. Classificazione:
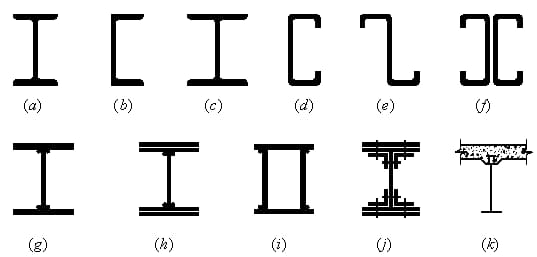
(1) Web solido: il web
Sezione in acciaio a forma di H: Facile da lavorare, semplice da produrre e a basso costo.
Sezione composita: Quando l'acciaio a forma di H non è in grado di soddisfare i requisiti di resistenza e rigidità.
(2) Struttura reticolare:
Quando la luce supera i 40 m, è meglio utilizzare una capriata a traliccio.
3. Griglia a raggiera:
Un sistema planare composto da travi principali e secondarie che si intersecano verticalmente e orizzontalmente.
(1) Griglia di raggi semplificata: Singolo fascio principale.
(2) Reticolo di travi ordinarie: Divisa in travi principali e secondarie.
(3) Griglia di travi composte: Divisa in travi principali, travi secondarie orizzontali e verticali.
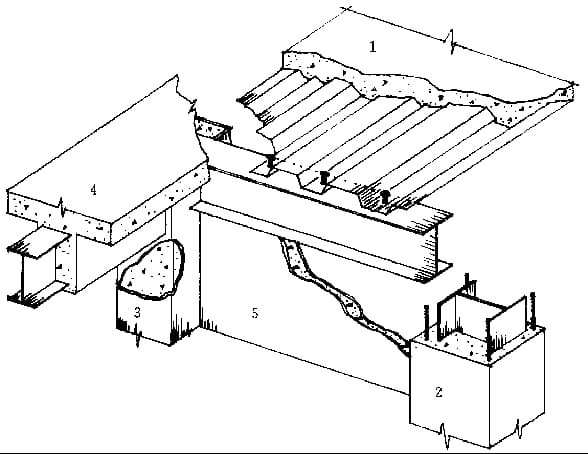
4. Interazione tra travi e piastre:
(1) Lavorazione in comune: Soletta composita.
(2) Lavoro non cooperativo: Lastra generale in cemento armato.
Lo sviluppo dello sforzo normale nella sezione trasversale può essere suddiviso in tre fasi:
(1) Fase elastica: Sotto carico dinamico.
(2) Fase elastica-plastica: Sotto carico statico o carico dinamico indiretto.
(3) Stadio di plastica:
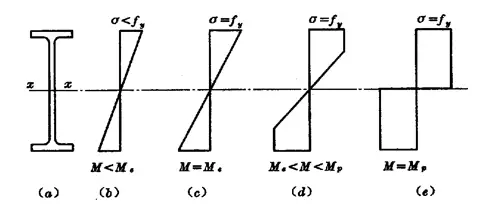
Capacità di flessione durante la fase elastoplastica di una sezione trasversale:
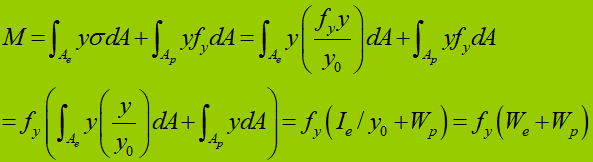
Per una sezione rettangolare:
(1) Fase elastica:
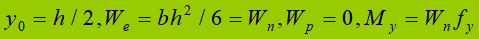
(2) Stadio di plastica:
(3) Fase elastoplastica:
Fattore di forma della sezione:
Sviluppo plastico a sezione parziale (1/4 di sezione, a = h/8) come stato limite:
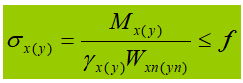
Nella formula:
γ è il fattore di sicurezza parziale per il momento, che può essere determinato in base alla Tabella 5.1 della Sezione 5 del codice di progettazione.
Ci sono due casi in cui il fattore di sicurezza parziale per il momento deve essere assunto pari a 1,0.
Metodo:
S:
La resistenza al taglio può essere calcolata utilizzando la teoria del flusso di taglio, assumendo che sia uniformemente distribuita lungo la direzione dello spessore della parete sottile.
(1) Quando si calcola la sollecitazione di taglio verticale in un punto qualsiasi dell'anima, è necessario calcolare il momento d'inerzia dell'area della sezione lorda al di sopra o al di sotto di tale punto rispetto all'asse neutro x.
(2) Quando si calcola la sollecitazione di taglio orizzontale in un punto qualsiasi della flangia, è necessario calcolare il momento d'inerzia dell'area della sezione lorda a sinistra o a destra di quel punto rispetto all'asse neutro x.
Dove tw è lo spessore della sezione nel punto in cui si calcola la sollecitazione di taglio.
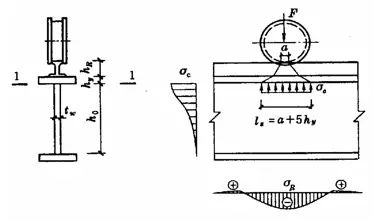
Quando la flangia di una trave è soggetta a un grande carico centrale fisso (comprese le reazioni dell'appoggio) e non sono previsti irrigidimenti, secondo la Figura 5-5 (a), o quando è soggetta a un carico concentrato mobile (come la pressione della ruota della gru), secondo la Figura 5-5 (b), è necessario calcolare la resistenza locale a compressione al bordo dell'altezza dell'anima. Supponendo che il carico concentrato si propaghi dal punto di applicazione a un intervallo di altezza di hy con un rapporto di 1:2,5 e si diffonde con un rapporto di 1:1 in un intervallo di altezza di hRè distribuito uniformemente sull'altezza del nastro calcolo del bordo. La σc è molto vicino alla massima pressione locale teorica. La resistenza locale alla compressione può essere calcolata con la seguente formula:
Nella formula,
Se il calcolo non è soddisfacente, il supporto o il carico concentrato fisso possono essere rinforzati con irrigidimenti trasversali o modificando le dimensioni della sezione. Tuttavia, quando si sopportano carichi concentrati mobili, si può modificare solo la dimensione della sezione.
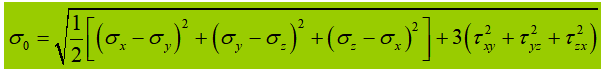
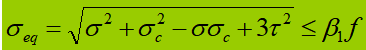
Quando il vibratore addominale è sottoposto a sollecitazioni normali, di taglio o di compressione locali significative all'altezza calcolata, è necessario calcolare la sollecitazione equivalente in quel punto.
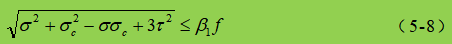
Nella formula:
σ, τ, σc - sforzo normale di flessione, sforzo di taglio e sforzo di compressione locale nello stesso punto dell'altezza di calcolo della piastra addominale, positivo per lo sforzo di trazione e negativo per lo sforzo di compressione;
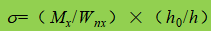
β1 - coefficiente per l'aumento del valore di progetto della resistenza a compressione in un punto locale. Quando σ e σc hanno lo stesso segno o σc=0, β1=1,1; quando σ e σc hanno segni opposti, β1=1.2.
Fenomeno di instabilità generale:
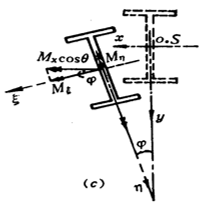
Analisi del meccanismo:
Dopo che la trave si è deformata per flessione, la flangia superiore è sottoposta a compressione. A causa dell'insufficiente rigidità laterale della trave, questa subirà una deformazione laterale di instabilità. La deformazione a flessione nel piano causata dal momento si verifica anche insieme alla deformazione torsionale dovuta alla flessione ineguale dall'alto verso il basso della sezione della trave.
Pertanto, l'instabilità complessiva della trave assume la forma di instabilità flesso-torsionale o, più precisamente, di instabilità laterale e torsionale.
(1) C1, C2, C3 - In relazione al tipo di carico
(2) Iy, Iw, It - Momento d'inerzia della sezione trasversale
(3) L - Lunghezza non controventata in direzione laterale
(4) a - Posizione del punto di azione nella direzione dell'altezza.
(5) 
| Condizione di carico | Coefficiente | ||
| G | C2 | G | |
| Carico concentrato a metà campata | 1.35 | 0.55 | 0.41 |
| Carico uniformemente distribuito sull'intera campata | 1.13 | 0.46 | 0.53 |
| Curvatura pura | 1.00 | 0.00 | 1.00 |
I principali fattori che influenzano la stabilità complessiva delle travi in acciaio sono:
(1) La lunghezza non controventata in direzione laterale o la distanza L1 tra il punto di appoggio laterale della flangia compressa. Più piccolo è il valore di L1, migliore è la stabilità complessiva della trave e maggiore è il momento flettente critico.
(2) Le dimensioni della sezione trasversale, compresi i vari momenti d'inerzia. Maggiore è il momento d'inerzia, migliore è la stabilità complessiva della trave. In particolare, aumentando la larghezza della flangia compressa b1 può aumentare anche il valore di βy nella formula.
(3) I vincoli sulla sezione da parte degli appoggi di estremità della trave. Se è possibile migliorare i vincoli sulla rotazione intorno all'asse y della sezione, la stabilità complessiva della trave migliorerà notevolmente.
(4) Tipo di carico: Flessione pura, carico uniformemente distribuito, carico concentrato a metà campata.
(5) La posizione del punto di azione del carico lungo la direzione dell'altezza della sezione trasversale, un valore; negativo per la flangia superiore e positivo per la flangia inferiore.
Curvatura su un solo piano:
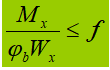
1. Sezione trasversale saldata a forma di "I", a simmetria biassiale, pura. carico di flessione.
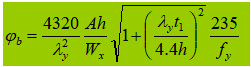
2. Sezione trasversale a I saldata, simmetrica monoassiale (effetti della sezione trasversale asimmetrica e dei diversi carichi)
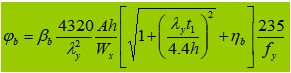
Se φb>0,6, il coefficiente di stabilità è considerato come:
3. Trave laminata ordinaria a forma di I in acciaio a semplice appoggio.
4. Trave a semplice sostegno in acciaio laminato a caldo.
5. Una trave a sbalzo a forma di I simmetrica su due assi.
La flangia compressa della trave è ricoperta da un impalcato (in cemento armato o lamiera d'acciaio) e saldamente collegati per evitare lo spostamento laterale della flangia compressa.
Per le travi H o I semplicemente appoggiate, il rapporto tra la lunghezza libera L1 e la larghezza b della flangia compressa non deve superare il valore specificato nella Tabella 5.4.
Tabella 5.4: Valore massimo di L1/b1 per il quale non è richiesto il calcolo della stabilità globale per le travi H o I semplicemente appoggiate.
| Grado di acciaio | Una trave senza punti di appoggio laterali a metà dell'apertura. | Una trave con una flangia sottoposta a compressione per tutta la campata e con punti di appoggio laterali, indipendentemente dal punto in cui viene applicato il carico. | |
| Il carico è applicato alla flangia. | Il carico è applicato alla flangia inferiore. | ||
| Q235 | 13.0 | 20.0 | 16.0 |
| Q345 | 10.5 | 16.5 | 13.0 |
| Q39 | 10.0 | 15.5 | 12.5 |
| Q420 | 9.5 | 15.0 | 12.0 |
1. Determinare se è necessaria una verifica della stabilità complessiva.
2. Calcolare i parametri della sezione.
3. Ottenere il coefficiente di momento flettente critico equivalente βb in base alle condizioni di carico.
4. Sostituire i valori nelle formule per ottenere il coefficiente di stabilità globale ϕb e verificare la stabilità globale.
Esempio: 5-2，5-3
Piastra flangiata: Il carico è relativamente semplice e la stabilità locale è garantita dalla limitazione del rapporto larghezza/spessore della piastra.
Piastra web: Il carico è complesso e per soddisfare i requisiti di resistenza, l'altezza della sezione è spesso elevata. Se continuiamo a limitare il rapporto altezza/spessore della piastra d'anima, il valore della piastra d'anima sarà molto grande e antieconomico. Pertanto, per ridurre le dimensioni della piastra e migliorare la capacità portante della stabilità locale, si ricorre generalmente agli irrigidimenti.
1. Irrigidimenti trasversali
2. Irrigidimenti longitudinali
3. Rinforzi corti
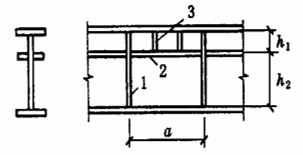
Principio di progettazione: principio della resistenza uguale.
Secondo la progettazione elastica (con γ=1,0 per non considerare lo sviluppo plastico), a causa dell'influenza di sollecitazione residua, la sezione trasversale effettiva è entrata nella fase elastoplastica. La "Specifica" prende Et=0.7E.
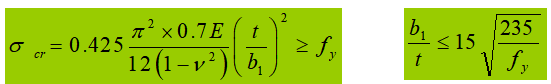
Se si considera lo sviluppo plastico (γ > 1,0), lo sviluppo plastico sarà maggiore e Et=0.5E.
| No. | Le condizioni della piastra web. | Specifiche della disposizione degli irrigidimenti | |
| 1 | 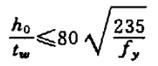 | στ=0 | Gli irrigidimenti possono essere omessi. |
| 2 | στ≠0 | Si raccomanda di installare irrigidimenti trasversali che soddisfino i requisiti strutturali e di calcolo. | |
| 3 |  | Si raccomanda di installare irrigidimenti trasversali che soddisfino i requisiti strutturali e di calcolo. | |
| 4 |  La flangia compressa è bloccata contro la torsione. | Gli irrigidimenti longitudinali devono essere aggiunti nella zona di compressione della sezione, dove le sollecitazioni di flessione sono elevate, rispettando i requisiti strutturali e di calcolo. | |
| 5 | 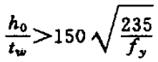 La flangia compressa è libera di ruotare. | ||
| 6 | Se necessario ai fini del calcolo. | ||
| 7 | Quando la tensione di compressione locale è elevata. | Se necessario, per soddisfare i requisiti strutturali e di calcolo, nella zona di compressione devono essere disposti degli irrigidimenti corti. | |
| 8 | In corrispondenza dell'appoggio della trave | Si consiglia di installare irrigidimenti di supporto che soddisfino i requisiti strutturali e di calcolo. | |
| 9 | Quando la flangia è soggetta a un grande carico concentrato fisso. | ||
| 10 | In ogni caso |  | |
1. Buckling di piastre composite sollecitate
È configurata solo la piastra d'anima con irrigidimenti trasversali.
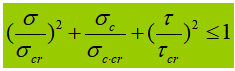
La piastra d'anima è configurata con irrigidimenti trasversali e longitudinali allo stesso tempo.
(1) Tra la flangia compressa e gli irrigidimenti longitudinali.
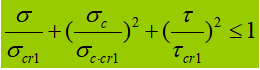
(2) Tra la flangia di trazione e gli irrigidimenti longitudinali.
Tra la flangia compressa e gli irrigidimenti longitudinali vengono installati corti irrigidimenti trasversali.
2. Requisiti costruttivi degli irrigidimenti per la piastra d'anima
(1) irrigidimenti trasversali in acciaio configurati a coppie su entrambi i lati della piastra d'anima.
Larghezza sporgente verso l'esterno:
Spessore:
(2) irrigidimenti trasversali in acciaio configurati su un lato della piastra d'anima.
Larghezza sporgente verso l'esterno: deve essere superiore a 1,2 volte il valore calcolato in base alla formula precedente.
Spessore: non deve essere inferiore a 1/15 della sua larghezza sporgente verso l'esterno.
(3) Nella piastra d'anima rinforzata con irrigidimenti trasversali e longitudinali, gli irrigidimenti longitudinali devono essere scollegati alle loro intersezioni mentre gli irrigidimenti trasversali rimangono continui.
Anche il momento d'inerzia attorno all'asse z deve soddisfare:
(4) Trattamento dell'estremità degli irrigidimenti trasversali:
3. Rinforzi per il supporto
(1) Calcolo della stabilità:
La stabilità degli irrigidimenti per il supporto è calcolata come un membro di compressione soggetto a carichi concentrati fissi o a reazioni di supporto della trave lungo il suo asse. L'area della sezione trasversale A di questo elemento di compressione comprende sia l'area dell'irrigidimento che quella della piastra d'anima entro 15tw su ciascun lato dell'irrigidimento. La lunghezza di calcolo è approssimativamente considerata come h0.
(2) Calcolo della resistenza alla compressione:
L'estremità degli irrigidimenti di supporto per le travi deve essere calcolata in base al carico concentrato fisso o alla reazione di supporto che sopportano. Quando l'estremità degli irrigidimenti è tagliata piatta e tesa, la sollecitazione di compressione sulla faccia terminale deve essere calcolata come segue:
dove:
Fasi di progettazione degli irrigidimenti trasversali a piastra d'anima:
1. Determinare se è necessario installare le barre trasversali;
2. Installare le traverse e determinare la distanza a, bs, ts;
3. Verificare lo stato di sollecitazione composito della piastra d'anima;
4. Verifica dell'irrigidimento di supporto: compresa la saldatura (collegamento tra le traverse e la piastra d'anima), verifica della stabilità alla compressione assiale (stabilizzazione al di fuori del piano dell'asse z) e verifica della resistenza.
Esempio 5-3: in base alle condizioni e ai risultati dell'Esempio 5-2, verificare se la sezione della trave principale mostrata nella Figura 5-9(b) soddisfa i requisiti. La trave principale è una trave semplicemente appoggiata a entrambe le estremità, realizzata in acciaio Q235 e saldata con elettrodi manuali della serie E43.
Soluzione:
1. Capacità di carico della trave principale:
Il diagramma di calcolo semplificato della trave principale è mostrato nella Figura 5-9(a). La pressione esercitata sulla trave principale dalle travi secondarie su entrambi i lati è di 2×73,69+2×2,33=152,04 kN, e la pressione delle travi secondarie all'estremità della trave è la metà di quella della trave secondaria centrale.
La reazione di appoggio della trave principale è R=2×152,04=304,08 kN.
Il momento flettente massimo della trave è M=(304,08-76,02)x5-152,04×2,5=760,2 kN.m
2. Calcolare le caratteristiche della sezione:
A=131,2 cm², Ix=145449 cm⁴, Wx=3513,3 cm³. Il peso proprio della trave principale è 131,2×10²x7850x10-⁶x1,2=123,6 kg/m=1,211 kN/m. Il fattore 1,2 è per considerare l'aumento del coefficiente dell'irrigidimento della trave principale. Il valore di progetto del momento flettente dopo aver considerato il peso della trave principale è M=760,2+1,2×1,211×10²/8=760,2+18,2=778,4 kN-m.
Considerando il valore di progetto della forza di reazione sull'appoggio dopo aver tenuto conto del peso proprio della trave principale, R=304,08+1,2×1,211×10/2=304,08+7,27=311,3kN.
3. Controllo della forza
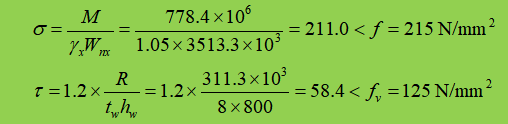
Gli irrigidimenti di supporto sono previsti in corrispondenza della connessione della trave secondaria e non vi è alcuna sollecitazione locale di compressione. Inoltre, poiché la sollecitazione di taglio è relativamente piccola, non è necessario verificare le altre sollecitazioni convertite in sezione.
4. Sulla trave secondaria è presente una piastra rigida che garantisce la stabilità della trave secondaria e può fungere da punto di appoggio laterale per la trave principale.
A questo punto, poiché l1/b1=2500/240=10,4<16, la stabilità complessiva può essere garantita senza calcoli.
5. Controllo della rigidità
Il valore standard totale del carico trasmesso dalla trave secondaria è FT=(15.5+0.52)×7.5=120.2kN, therefore,
Il valore standard totale del carico trasmesso dalla trave secondaria è FQ=2.5×4.2×7.5=78.75kN, therefore,
6. Stabilità locale
Flangia: b/t=(120-4)/14=8,3<13, che soddisfa il requisito di stabilità locale, e γx può essere assunto pari a 1,05; piastra: h0/tw=800/8=100, è necessario prevedere irrigidimenti trasversali, i dettagli sono omessi.
Dopo la deformazione della lastra sottile, si generano tensioni trasversali di trazione al centro della lastra, che limitano ulteriormente la deformazione longitudinale di flessione della lastra, consentendole di continuare a sopportare l'aumento della pressione.
1. Capacità portante a taglio dopo l'instabilità: Formula (5-94)
2. La capacità portante a taglio comprende due parti: Forza di taglio di instabilità (resistenza all'instabilità) + forza di taglio in campo di tensione (resistenza dopo l'instabilità).
3. Forza di taglio nel campo di tensione:
(1) Metodo del campo di tensione (complesso);
(2) Specifiche del codice.
Considerando che la capacità portante a flessione della piastra d'anima diminuisce leggermente dopo l'instabilità.
Due ipotesi:
(1) Altezza effettiva;
(2) Simmetria tra zona di tensione e zona di compressione.
La formula per il calcolo della capacità portante:
Nella formula,
Ciò indica che:
(1) Quando M sulla sezione è inferiore a Mf che la flangia può sopportare, la piastra d'anima può sopportare la forza di taglio Vu;
(2) Quando V sulla sezione è inferiore a 0,5 V, prendere M = Mue.
(1) Se gli irrigidimenti di supporto da soli non possono soddisfare l'equazione (5.99), è necessario aggiungere irrigidimenti trasversali accoppiati su entrambi i lati dell'anima per ridurre la lunghezza della regione di instabilità.
(2) Le dimensioni della sezione trasversale degli irrigidimenti trasversali devono soddisfare i requisiti costruttivi degli irrigidimenti dell'anima secondo l'equazione 5.85.
(3) In base alle specifiche della struttura in acciaio, l'irrigidimento trasversale centrale deve essere considerato come un elemento di compressione assiale e la sua stabilità al di fuori del piano dell'anima deve essere calcolata in base alla forza assiale utilizzando la seguente formula:
Quando l'irrigidimento è sottoposto a un carico trasversale concentrato F, Ns deve essere aumentato di F.
Calcolare il valore di progetto del momento flettente massimo Mmassimo per la trave in base alle condizioni reali.
Determinare il modulo di sezione richiesto in base alla resistenza alla flessione e alla stabilità complessiva:
Determinare la sezione dell'acciaio in base alle tabelle di sezione.
Verifica della sezione:
(1) Verifica della resistenza: flessione, taglio, compressione locale e sollecitazione equivalente.
(2) Verifica della rigidità: verifica del rapporto tra flessione e campata della trave.
(3) Verifica della stabilità complessiva (la stabilità locale della sezione in acciaio di solito non richiede verifiche).
(4) Regolare la sezione in base ai risultati della verifica ed eseguire nuovamente la verifica finché non soddisfa i requisiti di progetto.
1) Determinare il modulo di sezione richiesto in base alle condizioni di carico.
2) Determinare l'altezza della trave:
Altezza selezionata: hmin ≤ h ≤ hmassimo.
3). Determinare lo spessore dell'anima (assumendo che tutte le forze di taglio siano sostenute dall'anima), quindi:
In alternativa, lo spessore del nastro può essere determinato utilizzando formule empiriche:
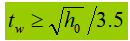
4). Determinare la larghezza della flangia:
Dopo aver determinato lo spessore dell'anima, l'area della flangia Af può essere determinato in base ai requisiti di resistenza alla flessione. Prendiamo come esempio una sezione a forma di I:
Una volta Af è determinato, si può scegliere b o t per determinare l'altro valore.
5). Verifica della sezione:
6). Calcolo delle saldature tra anima e flangia
La saldatura di collegamento viene utilizzata principalmente per resistere flessione-taglioe il taglio per unità di lunghezza è:
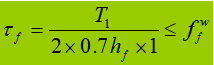
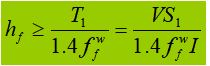
Quando la trave è soggetta a un carico concentrato fisso senza irrigidimenti di supporto, la saldatura della flangia superiore sopporta sia la forza di taglio T1 e la forza concentrata F. La forza per unità di lunghezza generata da F è V1:
Scopo: Per risparmiare acciaio e gestire le variazioni del momento flettente.
Metodi di modifica delle sezioni:
Punti da notare:
1. Classificazione:
2. Metodi di giunzione per sezioni di acciaio laminato:
3. Tecniche di giunzione di travi composite:
Considerazioni chiave:
1. Collegamenti primari e secondari di travi in acciaio:
2. Tipi di supporto delle travi:
Considerazioni chiave sulla progettazione:
In qualità di fondatore di MachineMFG, ho dedicato oltre un decennio della mia carriera al settore della lavorazione dei metalli. La mia vasta esperienza mi ha permesso di diventare un esperto nei campi della fabbricazione di lamiere, della lavorazione, dell'ingegneria meccanica e delle macchine utensili per metalli. Penso, leggo e scrivo costantemente su questi argomenti, cercando di essere sempre all'avanguardia nel mio campo. Lasciate che le mie conoscenze e la mia esperienza siano una risorsa per la vostra azienda.
IT 
EN 
AR 
DE 
ES 
FR 
JA 
NL 
PT 
PT_BR 
RU 
KO