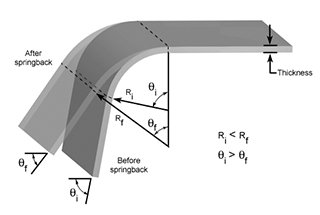
Vi siete mai chiesti perché alcune parti metalliche si ritraggono dopo la piegatura? In questo articolo esploreremo l'affascinante mondo degli stampi di piegatura e come prevedere con precisione il ritorno elastico. Imparerete consigli pratici e formule per ottenere risultati precisi nei vostri progetti di lavorazione del metallo.
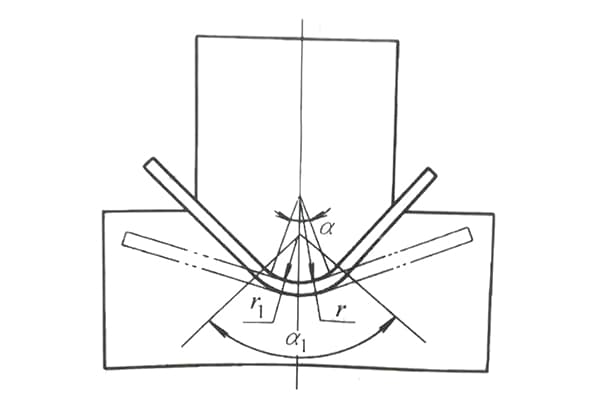
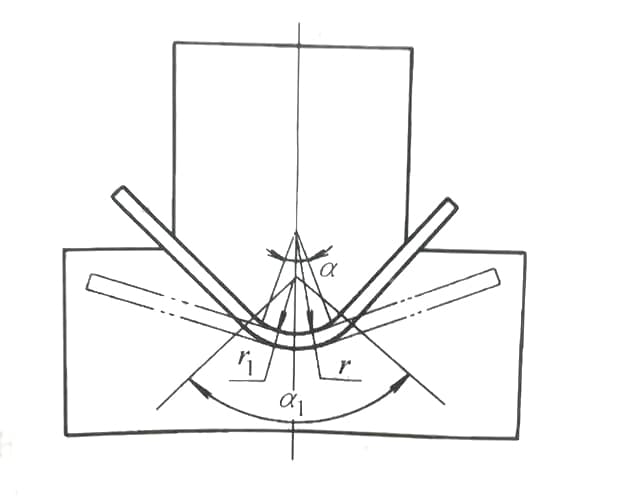
Quando si progetta uno stampo di piegatura con arco interno, la precisione e il comportamento del materiale sono fattori critici spesso trascurati negli approcci convenzionali. Molti progettisti trascurano completamente il ritorno elastico, utilizzando lo stesso raggio (R) del prodotto finito, oppure applicano un fattore di riduzione rudimentale al valore R senza considerare le complessità delle proprietà e delle geometrie dei materiali.
Ad esempio, una pratica comune per un prodotto con un valore R originale di 1 mm prevede la riduzione del raggio convesso dello stampo di un fattore 0,8 per i materiali più duri o 0,9 per quelli più morbidi. Questo approccio semplicistico, pur essendo talvolta efficace per le applicazioni di base, manca delle sfumature necessarie per le specifiche più esigenti.
I limiti di questo metodo diventano particolarmente evidenti quando si tratta di materiali sottili e di grandi raggi. Si consideri un prodotto con uno spessore di 0,5 mm e un raggio interno di 200 mm. In questi casi, prevedere con precisione il ritorno elastico diventa difficile a causa della complessa interazione tra proprietà del materiale, rapporto spessore/raggio e angolo di flessione.
Per ovviare a queste limitazioni e migliorare la precisione nella progettazione degli stampi, è necessario un approccio più sofisticato. La sezione seguente introduce una formula universale per il ritorno elastico che tiene conto di vari parametri geometrici e del materiale, consentendo calcoli più accurati basati su input numerici. Questo metodo fornisce una base solida per la progettazione di stampi in un'ampia gamma di applicazioni e materiali.
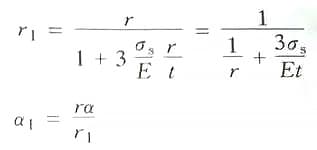
Nella formula:
Assumendo 3σs/E=A come coefficiente di semplificazione, con i valori elencati nella Tabella 2-27. La formula di calcolo per il raggio d'angolo convesso della matrice durante la flessione di barre a sezione circolare è la seguente:

Il valore di A è riportato nella tabella seguente.
| Scienza dei materiali | Stato | A | Scienza dei materiali | Stato | A |
| 1035(L4) 8A06(L6) | ricottura | 0.0012 | QBe2 | morbido | 0.0064 |
| Durezza a freddo | 0.0041 | duro | 0.0265 | ||
| 2A11(LY11) | morbido | 0.0064 | QA15 | duro | 0.0047 |
| duro | 0.0175 | 08, 10, Q215 | 0.0032 | ||
| 2A12(LY12) | morbido | 0.007 | 20, Q235 | 0.005 | |
| duro | 0.026 | 30, 35, Q255 | 0.0068 | ||
| T1, T2, T3 | morbido | 0.0019 | 50 | 0.015 | |
| duro | 0.0088 | T8 | ricottura | 0.0076 | |
| H62 | morbido | 0.0033 | durezza a freddo | ||
| semi-duro | 0.008 | ICr18N9Ti | ricottura | 0.0044 | |
| duro | 0.015 | durezza a freddo | 0.018 | ||
| H68 | morbido | 0.0026 | 65Mn | ricottura | 0.0076 |
| duro | 0.0148 | durezza a freddo | 0.015 | ||
| QSn6,5-0,1 | duro | 0.015 | 60Si2MnA | ricottura | 0.125 |
Se i materiali necessari non sono disponibili, è possibile consultare la tabella sottostante per trovare i materiali necessari. modulo di elasticità e la resistenza allo snervamento del materiale, per poi sostituirli nella formula di calcolo precedente.
| Nome del materiale | Grado del materiale | Stato del materiale | Forza definitiva | Velocità di allungamento(%) | Resistenza allo snervamento/MPa | Modulo elasticoE/MPa | |
| resistenza al taglio/MPa | trazione/MPa | ||||||
| Acciaio strutturale al carbonio | 30 | Normalizzato | 440-580 | 550-730 | 14 | 308 | 22000 |
| 55 | 550 | ≥670 | 14 | 390 | – | ||
| 60 | 550 | ≥700 | 13 | 410 | 208000 | ||
| 65 | 600 | ≥730 | 12 | 420 | – | ||
| 70 | 600 | ≥760 | 11 | 430 | 210000 | ||
| Acciaio strutturale al carbonio | T7~T12 T7A-T12A | Ricotto | 600 | 750 | 10 | – | – |
| T8A | Indurito a freddo | 600-950 | 750-1200 | – | – | – | |
| Acciaio al carbonio di alta qualità | 10Mn2 | Ricotto | 320-460 | 400-580 | 22 | 230 | 211000 |
| 65M | 600 | 750 | 18 | 400 | 211000 | ||
| Acciaio strutturale legato | 25CrMnSiA 25CrMnSi | Ricotto a bassa temperatura | 400-560 | 500-700 | 18 | 950 | – |
| 30CrMnSiA 30CrMnSi | 440-600 | 550-750 | 16 | 1450850 | – | ||
| Acciaio per molle di alta qualità | 60Si2Mn 60Si2MnA 65Si2WA | Ricotto a bassa temperatura | 720 | 900 | 10 | 1200 | 200000 |
| Indurito a freddo | 640-960 | 800-1200 | 10 | 14001600 | – | ||
| Acciaio inox | 1Cr13 | Ricotto | 320-380 | 400-170 | 21 | 420 | 210000 |
| 2Cr13 | 320-400 | 400~500 | 20 | 450 | 210000 | ||
| 3Cr13 | 400-480 | 500~600 | 18 | 480 | 210000 | ||
| 4Cr13 | 400-480 | 500-500 | 15 | 500 | 210000 | ||
| 1Cr18Ni9 2Cr18Ni9 | Trattato termicamente | 460~520 | 580-610 | 35 | 200 | 200000 | |
| Temprato a freddo | 800-880 | 100-1100 | 38 | 220 | 200000 | ||
| 1Cr18Ni9Ti | Trattato termicamente e ammorbidito | 430~550 | 54-700 | 40 | 240 | 200000 | |
È meglio creare un database di materiali comunemente utilizzati e ottenere i parametri fisici mancanti dai fornitori. Se i parametri per il modulo elastico e resistenza allo snervamento sono corretti, la piegatura e il rimbalzo di terminali a molla generici, parti estetiche e profili sono più precisi.