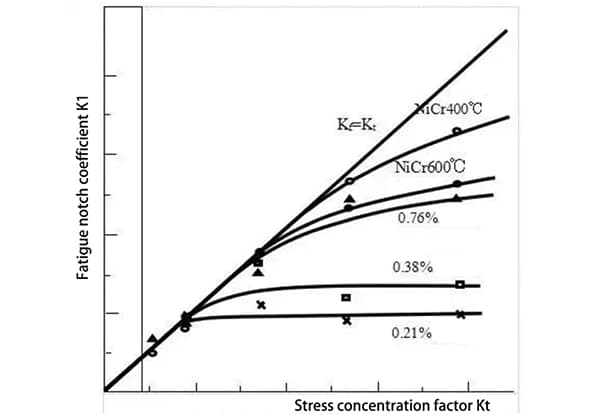
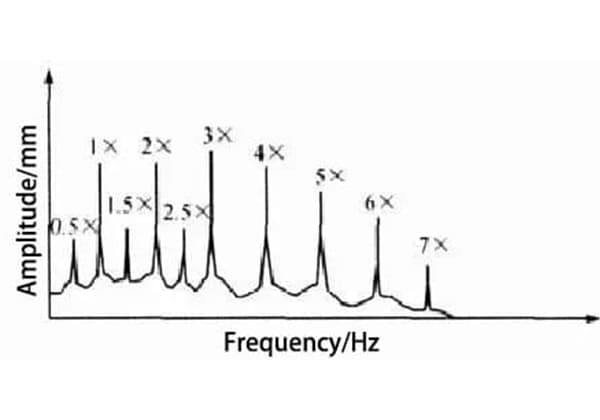
Come fanno gli ingegneri a prevedere quando un materiale si romperà in seguito a sollecitazioni ripetute? Questo articolo introduce la curva S-N, uno strumento chiave nell'analisi della fatica. Imparerete come vengono trattate le sollecitazioni medie, la conversione delle sollecitazioni multiassiali e le sollecitazioni irregolari per prevedere la vita a fatica del materiale. La comprensione di questi concetti può aiutare a progettare componenti più durevoli e affidabili. Continuate a leggere per esplorare le complessità dell'analisi della fatica e garantire la longevità dei vostri progetti di ingegneria.
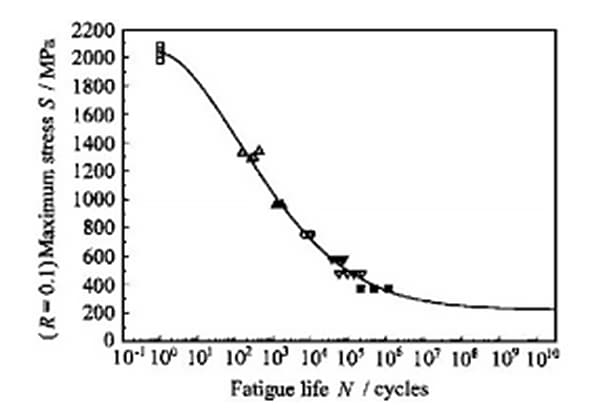
Le proprietà di fatica dei materiali sono tipicamente espresse attraverso cicli di sollecitazione uniassiali, noti come curve S-N. È importante notare che in questo contesto non viene presa in considerazione la teoria della fatica basata sulla meccanica della frattura.
La variazione della sollecitazione nel tempo segue spesso un andamento regolare, come un'onda sinusoidale, un'onda quadra o un impulso. Tuttavia, l'influenza della sollecitazione media sulla prestazione a fatica è spesso trascurata (cioè, l'impatto di r=Smin/Smassimo ≠ -1).
Nella realtà, lo stato di sollecitazione è di solito multiassiale, con una variazione irregolare delle sollecitazioni e r≠-1. La corrispondenza tra le sollecitazioni reali e le prestazioni a fatica misurate in laboratorio, che prevedono una variazione regolare delle sollecitazioni, una sollecitazione uniassiale e r=1, costituisce la base per l'analisi della fatica.
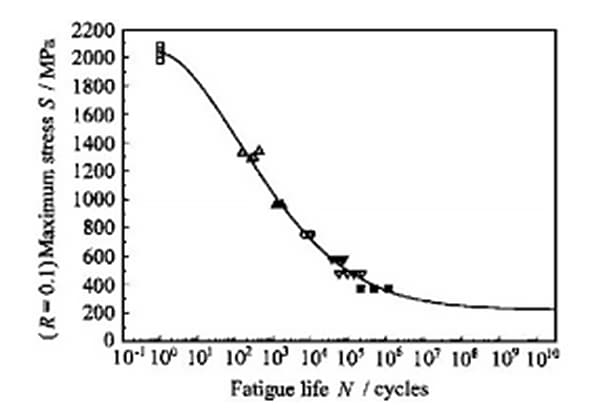
Quando sono disponibili curve S-N per diversi valori di r, si ricorre in genere al metodo dell'interpolazione per determinare la curva S-N per valori di r sconosciuti.
Nei casi in cui è disponibile solo una curva S-N con r=-1, è possibile utilizzare la seguente formula per calcolare la sollecitazione equivalente. Questa formula converte la sollecitazione uniassiale di r≠-1 nella sollecitazione uniassiale quando r=-1, nota come sollecitazione equivalente:
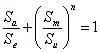
Dove, Sa è l'ampiezza di semisollecitazione, Se è la sollecitazione equivalente desiderata, Sm è la sollecitazione media e diversi valori di Su e n costituiscono teorie diverse:
Per determinare il tipo di sollecitazione utilizzata per la trasformazione sono disponibili le seguenti opzioni: sollecitazione equivalente di Von Mises, massima sollecitazione di taglio, massima sollecitazione principale o una componente specifica della sollecitazione (come Sx, Syz, ecc.).
A volte si utilizza anche la sollecitazione di Mises con un segno, mentre la sua grandezza rimane invariata. Il segno corrisponde al segno della sollecitazione principale massima. Un vantaggio di questo metodo è che permette di considerare gli effetti di tensione o compressione, che si riflettono nella sollecitazione media o r.
Simile al teoria della forzaLa conversione della sollecitazione equivalente di Von Mises e della massima sollecitazione di taglio è adatta a materiali con elevata duttilità, mentre la conversione della massima sollecitazione principale è appropriata per materiali fragili.
La curva temporale di sollecitazione uniassiale equivalente di alto e basso irregolare viene analizzata per estrarre una serie di cicli di sollecitazione semplice (Sa, Sm) e i loro tempi corrispondenti.
Il conteggio e le statistiche possono essere ottenuti con diversi metodi, tra cui il metodo dipendente dal percorso e il metodo indipendente dal percorso.
Per completare il processo di conteggio si applica il metodo della correlazione dei percorsi, che è il metodo di conteggio dei flussi di pioggia più diffuso. Il suo algoritmo e il suo principio sono spiegati in "Downing, S., Society, D. (1982) Simplified rain flow counting algorithms. Int J Fatigue, 4, 31-40".
Dopo il trattamento del flusso di pioggia, la curva irregolare del tempo di sollecitazione viene trasformata in una serie di cicli semplici (Sa, Sm, e ni, dove ni è il numero di cicli).
Questo metodo consente di applicare la teoria dell'accumulo dei danni (criterio di Miner) per calcolare e analizzare: Somma (ni/Ni), dove Ni è la vita corrispondente al ciclo di sollecitazione (considerando Sa, Smvedi sopra).
Questa tecnica è comunemente utilizzata per misurare il fattore di sicurezza dopo un certo numero di cicli o la vita corrispondente di uno specifico ciclo di sollecitazione complesso.
Attualmente, i software commerciali per l'analisi della fatica si basano per lo più sul processo sopra descritto.
Tuttavia, va notato che l'analisi della fatica è un'analisi empirica e che attualmente non esiste una teoria matura e completa.
Esistono diverse prospettive per quanto riguarda la conversione delle sollecitazioni multiassiali in monoassiali.
La sollecitazione di Von Mises, ad esempio, è una grandezza che si basa sull'idea dell'energia specifica del cambiamento di forma.
L'utilizzo dei concetti di positivo e negativo o di tensione e compressione è un metodo impreciso e non è consigliato.
La scelta del tipo di sollecitazione da adottare dipende dal possibile andamento delle cricche sui materiali o sulle strutture per determinare quale tipo di sollecitazione sia il fattore primario di controllo. rottura per fatica.
La pratica ingegneristica ha dimostrato che l'acciaio con una buona plasticità è spesso danneggiato a causa di ripetuti carichi dinamici di sollecitazione principale in casi di rottura per fatica.
Supplemento al trattamento dell'effetto stress medio:
"Se esistono curve S-N con valori R diversi, per determinare la curva S-N con valori R sconosciuti si utilizza generalmente il metodo dell'interpolazione".
Questo è solo un metodo, utile quando ci sono più sollecitazioni da controllare. Tuttavia, questo metodo può risultare macchinoso quando si controlla una sola vita di sollecitazione.
Un altro metodo consiste nel determinare la semiampiezza di sollecitazione equivalente nella condizione di R = -1, e quindi applicare direttamente la curva S-N.
In presenza di una sollecitazione media, la curva S-N non può essere utilizzata direttamente. Si deve invece utilizzare la CURVA DI GOODMAN o la CURVA DI GOODMAN modificata.
In qualità di fondatore di MachineMFG, ho dedicato oltre un decennio della mia carriera al settore della lavorazione dei metalli. La mia vasta esperienza mi ha permesso di diventare un esperto nei campi della fabbricazione di lamiere, della lavorazione, dell'ingegneria meccanica e delle macchine utensili per metalli. Penso, leggo e scrivo costantemente su questi argomenti, cercando di essere sempre all'avanguardia nel mio campo. Lasciate che le mie conoscenze e la mia esperienza siano una risorsa per la vostra azienda.
IT 
EN 
AR 
DE 
ES 
FR 
JA 
NL 
PT 
PT_BR 
RU 
KO