Comprendere la teoria delle quattro forze: Punti chiave da conoscere

1. Teoria della massima tensione di trazione (la prima teoria della resistenza è la massima tensione principale):

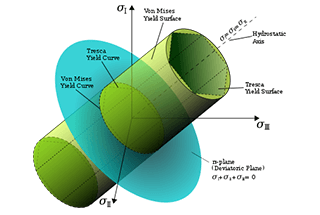
Questa teoria è comunemente chiamata teoria della prima resistenza. Essa sostiene che la causa principale della rottura è la massima sollecitazione di trazione. Se la prima sollecitazione principale raggiunge il limite di resistenza alla trazione monoassiale, indipendentemente dalla complessità o dalla semplicità dello stato di sollecitazione, si verifica la frattura.

Forma di rottura: Frattura

Condizioni di danno: σ1 =σb

Condizione di resistenza: σ1≤[σ]

Gli esperimenti hanno dimostrato che questa teoria della resistenza può spiegare meglio il fenomeno della frattura di materiali fragili come la pietra e la ghisa, in particolare nelle zone in cui si trova la massima tensione di trazione. Tuttavia, non è adatta ai casi in cui non c'è tensione di trazione, come la compressione unidirezionale o la compressione tridirezionale.

Svantaggio: non considera le altre due sollecitazioni principali.

Ambito di applicazione: Questa teoria è adatta alla tensione di materiali fragili, come l'allungamento e la torsione della ghisa.

2. Teoria della deformazione lineare a massimo allungamento (la seconda teoria della resistenza è la massima deformazione principale)

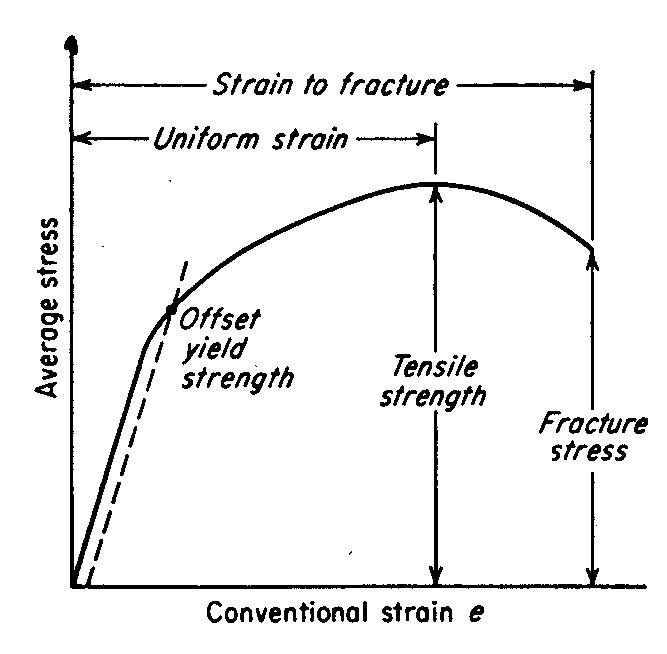
Questa teoria è comunemente chiamata teoria della seconda resistenza. Essa sostiene che la causa principale della rottura è la massima deformazione lineare di allungamento. Se la prima deformazione principale raggiunge il valore limite della tensione uniassiale, indipendentemente dalla complessità o dalla semplicità dello stato di sollecitazione, si verifica la frattura.

Ipotesi di rottura: La deformazione massima di allungamento raggiunge il limite della tensione semplice (supponendo che la legge di Hooke possa ancora essere usata per calcolare fino alla frattura).

Forma di rottura: Frattura

Condizioni di frattura fragile: ε1 = εu = σb/E;

ε1 = 1/E [σ1-μ(σ2+σ3)];

Condizioni di danno: σ1-μ(σ2+σ3) = σb;

Condizione di resistenza: σ1-μ(σ2+σ3)≤[σ]

Gli esperimenti hanno dimostrato che questa teoria della resistenza può spiegare meglio il fenomeno della frattura di materiali fragili come la pietra e il calcestruzzo sotto tensione assiale. Tuttavia, è stata utilizzata raramente perché i suoi risultati sperimentali sono coerenti solo con alcuni materiali e non possono spiegare ampiamente la legge generale della rottura fragile.

Svantaggi: Non spiega la legge generale della rottura fragile.

Ambito di applicazione: Questa teoria è adatta alla compressione assiale di pietra e calcestruzzo.

3. Teoria della massima sollecitazione di taglio (la terza teoria della resistenza, ovvero la resistenza di Tresca):

Questa teoria, nota come teoria della terza resistenza, sostiene che la causa principale della rottura è la massima sollecitazione di taglio (τmax). La teoria afferma che, indipendentemente dalla complessità o dalla semplicità dello stato di sollecitazione, una volta che la massima sollecitazione di taglio raggiunge il valore della sollecitazione di taglio ultima sotto tensione monoassiale, si verifica lo snervamento.

L'ipotesi di rottura è che quando la massima sollecitazione di taglio in uno stato di sollecitazione complesso raggiunge il limite di sollecitazione di taglio del materiale durante la semplice tensione e compressione, si verificherà la rottura sotto forma di snervamento. Il fattore principale che contribuisce alla rottura è la massima sollecitazione di taglio, che è uguale alla sollecitazione di taglio ultima (τmax=τu=σs/2).

La condizione di rottura per snervamento è definita come τmax=1/2(σ1-σ3), e le condizioni di danno sono soddisfatte quando σ1-σ3=σs. La condizione di resistenza è indicata come σ1-σ3≤[σ].

Gli esperimenti hanno dimostrato che questa teoria fornisce una migliore spiegazione della deformazione plastica dei materiali plastici. Tuttavia, va notato che questa teoria non tiene conto dell'influenza di 2σ e, di conseguenza, i componenti progettati sulla base di questa teoria tendono a essere eccessivamente conservativi.

Svantaggi: nessuno 2 σ influenza

Ambito di applicazione: adatto alle condizioni generali dei materiali plastici.

La forma è semplice, il concetto è chiaro e i macchinari sono ampiamente utilizzati.

Ma il risultato teorico è più sicuro di quello reale.

4. Teoria dell'energia specifica del cambiamento di forma (quarta teoria della forza, ovvero la forza di von mises)

Questa teoria è denominata teoria della quarta resistenza e sostiene che il motivo dello snervamento in un materiale è l'energia specifica (DU) del cambiamento di forma che raggiunge un certo valore limite, indipendentemente dallo stato di sollecitazione.

Le condizioni di danno sono definite come 1/2(σ1-σ2)2+2(σ2-σ3)2+(σ3-σ1)2=σs, e la condizione di resistenza è data come σr4= 1/2(σ1-σ2)2+ (σ2-σ3)2 + (σ3-σ1)2≤[σ].

I dati sperimentali ottenuti da prove su tubi sottili di diversi materiali (acciaio, rame, alluminio) hanno dimostrato che la teoria dell'energia specifica di variazione della forma è più in linea con i risultati sperimentali rispetto alla teoria della terza resistenza.

Una forma unificata delle quattro teorie della resistenza può essere stabilita avendo una sollecitazione equivalente (σrn) che ha un'espressione unificata della condizione di resistenza (σrn≤[σ]). La sollecitazione equivalente può essere espressa come segue:

σr1=σ 1≤[σ]

σr2=σ1-μ(σ2+σ3)≤[σ]

σr3=σ1-σ3≤ [σ]

σr4= 1/2(σ1-σ2)2+(σ2-σ3)2+(σ3-σ1)2≤ [σ]

5. Teoria della forza di Mohr

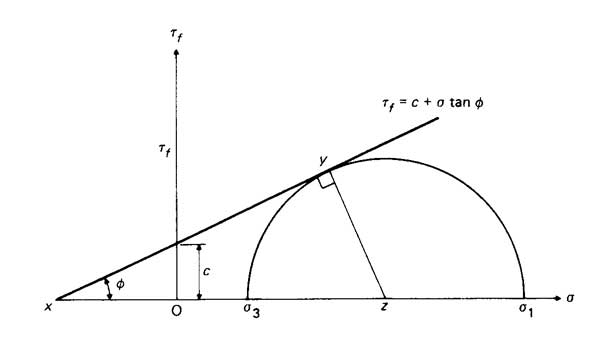
La teoria della resistenza di Mohr non si basa sul presupposto che la rottura dei materiali sia causata da un singolo fattore (come la sollecitazione, la deformazione o l'energia specifica) che raggiunge il suo valore limite. Si tratta invece di una teoria della resistenza che si basa sui risultati di prove di rottura di materiali sottoposti a vari stati di sollecitazione.

Questa teoria considera le differenze tra le resistenze a trazione e a compressione dei materiali, riconosce la massima sollecitazione di taglio come causa principale dello snervamento e tiene conto dell'influenza della sollecitazione normale sul piano di taglio.

Sebbene la teoria della resistenza di Mohr riconosca le diverse capacità di trazione e compressione dei materiali, il che è coerente con i materiali fragili (come la roccia e il calcestruzzo), non tiene conto dell'influenza della sollecitazione principale intermedia 2a, il che rappresenta una limitazione della teoria.

6. Ambito di applicazione della teoria della forza

La resistenza di un materiale non è determinata solo dalla natura del materiale stesso, ma anche dallo stato di sollecitazione nel punto di rottura.

I materiali fragili sono tipicamente analizzati utilizzando la teoria della resistenza alla frattura fragile o la teoria della resistenza di Mohr, mentre i materiali plastici sono analizzati utilizzando la teoria della resistenza allo snervamento.

Tuttavia, la modalità di rottura dei materiali è anche legata allo stato di sollecitazione. Ad esempio, in condizioni di sollecitazione di trazione tridimensionale, sia che un materiale sia plastico o fragile, esso cederà sotto forma di frattura, e si dovrà utilizzare la teoria della massima sollecitazione di trazione. In caso di sollecitazione tridimensionale di compressione, si verifica una deformazione plastica e si deve utilizzare la teoria della terza o quarta resistenza.