Vi siete mai chiesti perché un ponte può improvvisamente iniziare a tremare violentemente o perché un bicchiere di vino si frantuma quando un cantante fa un acuto? Questo blog esplora gli affascinanti concetti di frequenza naturale e frequenza di risonanza, rivelando il loro impatto su tutto, dalle meraviglie dell'ingegneria agli oggetti di uso quotidiano. Scoprite i segreti che si celano dietro queste vibrazioni e imparate come danno forma al nostro mondo.
Nell'analisi quotidiana, spesso confondiamo la frequenza naturale e la frequenza di risonanza, pensando che siano la stessa cosa.
In realtà, questo non è rigoroso.
La frequenza naturale è la prestazione delle caratteristiche naturali della struttura, mentre la frequenza di risonanza è la prestazione della risposta della struttura alle forze esterne.
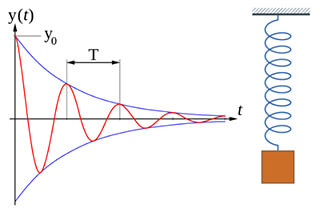
Un sistema a singolo grado di libertà è un sistema in cui la posizione può essere determinata completamente da una sola coordinata generalizzata in qualsiasi momento. In termini più semplici, la forza che agisce su un corpo è in una sola direzione. Il movimento della bambola nella figura seguente può essere rappresentato come un sistema molla-massa.
La figura seguente mostra un modello semplificato del sistema massa-molla.
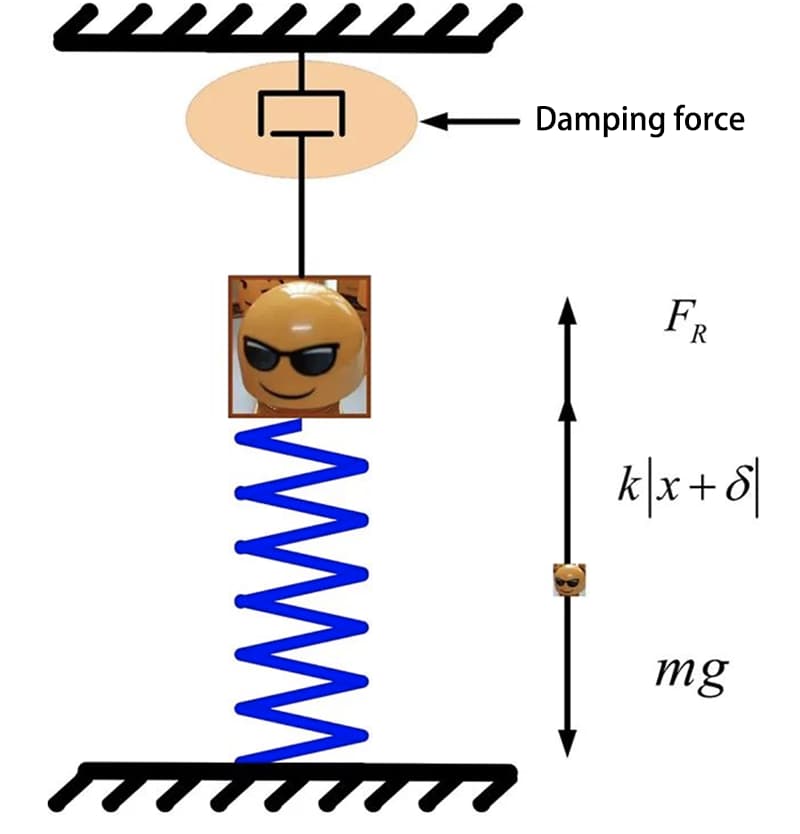
La posizione di equilibrio statico del blocco di prelievo è considerata l'origine delle coordinate ed è considerata positiva quando si muove verticalmente verso il basso lungo la direzione di deformazione della molla. La distanza tra il blocco e la posizione di equilibrio può essere rappresentata come x, e l'equazione differenziale del moto del blocco può essere espressa come:
Dove m è la massa del blocco, k è la rigidità della molla, c è il coefficiente di viscosità, 2n=c/m è il coefficiente di attenuazione dello smorzamento; quando il coefficiente di smorzamento è zero, corrisponde al sistema di vibrazione non smorzato.
Frequenza naturale Pn:
La frequenza naturale dipende solo dalla massa e dalla rigidità e non è influenzata da fattori come lo smorzamento. Connessioni strutturali al contorno, proprietà del materialeLa frequenza naturale può essere influenzata dalla forma e da altri fattori, ma queste influenze si riflettono sulla rigidità e sulla massa e non sono i fattori determinanti.
La vibrazione libera è la vibrazione del sistema senza eccitazione esterna e la traccia del movimento è legata allo stato iniziale e alle caratteristiche naturali.
La vibrazione forzata si riferisce alla vibrazione generata dal sistema sotto un'eccitazione esterna.
L'eccitazione esterna è generalmente una funzione periodica o aperiodica del tempo, tra cui l'eccitazione armonica semplice è la più semplice.
Sia la forza eccitante armonica semplice:
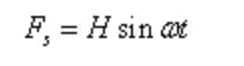
Dove H è l'ampiezza della forza eccitante, ω è la frequenza angolare della forza eccitante.
Quando il blocco si discosta dalla posizione di equilibrio di una distanza x, l'equazione differenziale del moto del blocco è
Dove h=H/m, l'equazione di cui sopra è l'equazione differenziale della vibrazione forzata di un singolo grado di libertà con smorzamento viscoso, che è un'equazione differenziale ordinaria non omogenea lineare a coefficiente costante del secondo ordine.
L'equazione di cui sopra è completamente coerente con l'espressione della risposta di tensione del carico capacitivo che abbiamo imparato nella teoria dei circuiti, che è un'equazione differenziale ordinaria non omogenea lineare a coefficiente costante del secondo ordine.
Lo smorzamento nel circuito dipende dalla resistenza, perché la resistenza consuma e non immagazzina energia.
Sotto semplice eccitazione armonica, la soluzione totale dell'equazione differenziale del moto di un sistema smorzato è data da:
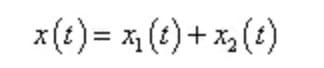
Dove, x1 (t) è una soluzione omogenea, che è una vibrazione libera attenuata;
A causa dell'esistenza dello smorzamento, la parte di vibrazione smorzata scomparirà dopo un certo periodo di tempo.
La soluzione è la stessa della vibrazione libera, quindi non verrà ripetuta in questa sede.
Qui ci occupiamo della soluzione speciale x2 (t) generato dalla vibrazione forzata, che può essere espresso come:
Tra questi,
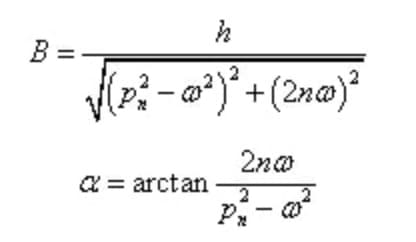
L'ampiezza e lo sfasamento della vibrazione forzata allo stato stazionario sono indipendenti dalle condizioni iniziali, ma dipendono solo dalle caratteristiche del sistema e dell'eccitazione.
Impostare il rapporto di frequenza, il rapporto di smorzamento e il coefficiente di amplificazione dell'ampiezza come segue:
La formula precedente può essere riscritta come:
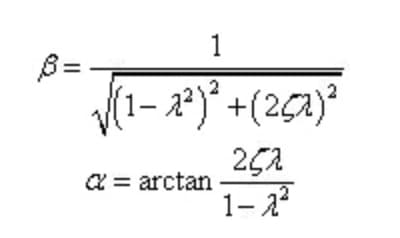
In base a ciò, possiamo conoscere la risposta del sistema sotto la vibrazione forzata.
Per una migliore comprensione, è possibile illustrare la relazione tra diversi rapporti di smorzamento, rapporti di frequenza e coefficienti di amplificazione dell'ampiezza. La frequenza è separata in tre regioni: bassa frequenza, media frequenza e alta frequenza. Come si vede nella figura, sia nella zona a bassa frequenza che in quella ad alta frequenza, lo smorzamento ha un impatto minimo sul coefficiente di amplificazione dell'ampiezza. Pertanto, il sistema smorzato può essere semplificato come un sistema non smorzato per facilitare il calcolo.
La frequenza naturale è una caratteristica intrinseca delle proprietà strutturali di un sistema, determinata esclusivamente dalla massa e dalla rigidità, indipendentemente da fattori esterni come lo smorzamento. In un sistema a n gradi di libertà esistono n frequenze naturali distinte, mentre i sistemi continui possiedono un numero infinito di frequenze naturali.
La risonanza si verifica quando una frequenza di eccitazione esterna corrisponde o coincide con la frequenza naturale di un sistema, facendo vibrare la struttura con un'ampiezza significativamente maggiore. Questo fenomeno è rappresentato dal cerchio blu nella figura seguente. La frequenza di risonanza, pur approssimandosi spesso alla frequenza naturale nei sistemi leggermente smorzati, può discostarsi da essa nelle strutture fortemente smorzate, essendo in genere inferiore alla frequenza naturale.
Nella progettazione del sistema, è fondamentale evitare non solo la frequenza di picco risonante specifica, ma anche la banda risonante circostante, corrispondente alla regione di frequenza intermedia della figura. Questa precauzione è necessaria perché la risposta del sistema rimane notevolmente amplificata all'interno di questa banda. I tecnici devono assicurarsi che né il normale funzionamento del sistema né le eccitazioni esterne provenienti da apparecchiature vicine rientrino in questo intervallo critico.
La risonanza può avere profonde implicazioni, sia benefiche che dannose. Gli effetti negativi possono includere il collasso di travi di sollevamento, la risonanza al suolo negli elicotteri, il danneggiamento di macchinari e i cedimenti strutturali indotti da infrasuoni. Al contrario, la risonanza viene deliberatamente utilizzata negli strumenti musicali per produrre i toni e le armoniche desiderate.
Per mitigare i rischi associati alla risonanza, i progettisti utilizzano diverse strategie:
La comprensione e la gestione della risonanza sono essenziali in campi che vanno dall'ingegneria civile e aerospaziale alla produzione di precisione e alla progettazione di strumenti musicali. Strumenti analitici avanzati, come l'analisi agli elementi finiti e l'analisi modale sperimentale, svolgono un ruolo cruciale nel prevedere e caratterizzare il comportamento di risonanza in sistemi complessi.
In qualità di fondatore di MachineMFG, ho dedicato oltre un decennio della mia carriera al settore della lavorazione dei metalli. La mia vasta esperienza mi ha permesso di diventare un esperto nei campi della fabbricazione di lamiere, della lavorazione, dell'ingegneria meccanica e delle macchine utensili per metalli. Penso, leggo e scrivo costantemente su questi argomenti, cercando di essere sempre all'avanguardia nel mio campo. Lasciate che le mie conoscenze e la mia esperienza siano una risorsa per la vostra azienda.
IT 
EN 
AR 
DE 
ES 
FR 
ID 
JA 
NL 
PT 
PT_BR 
RU 
KO 
TR