Vi siete mai chiesti come funzionano i piccoli rivetti che tengono insieme strutture enormi? In questo articolo sveleremo l'affascinante mondo delle connessioni a rivetto, esplorandone i tipi, i calcoli di resistenza e le applicazioni reali. Alla fine capirete il ruolo cruciale che questi piccoli componenti svolgono nelle meraviglie dell'ingegneria. Restate sintonizzati per scoprire come i rivetti tengono il nostro mondo saldamente fissato!
I rivetti sono un metodo fondamentale per unire due o più pezzi di materiale, in particolare di metallo, e sono ampiamente utilizzati in varie applicazioni ingegneristiche ed edilizie. I rivetti, che sono dispositivi di fissaggio meccanici permanenti, sono costituiti da un albero cilindrico liscio con una testa a un'estremità. Il processo di installazione prevede l'inserimento del rivetto in un foro preforato e la successiva deformazione dell'estremità posteriore per creare una seconda testa, fissando così i materiali tra loro.
Storicamente, i collegamenti rivettati sono stati essenziali nella costruzione di strutture importanti. Esempi notevoli sono la Torre Eiffel di Parigi e il Golden Gate Bridge di San Francisco. Queste strutture dimostrano la durata e la forza dei giunti rivettati, che hanno superato la prova del tempo e continuano a funzionare in modo affidabile.
La disposizione dei rivetti a catena, a zig-zag o sfalsati influenza le prestazioni del giunto.
I rivetti possono essere realizzati in diversi materiali, tra cui alluminio, acciaio, ottone e rame. La scelta del materiale dipende da requisiti specifici come la forza, la resistenza alla corrosione e la duttilità.
I giunti rivettati sono preferiti negli scenari in cui il giunto deve resistere a carichi dinamici e in cui è necessario unire materiali dissimili. Vengono scelti anche per il loro significato storico e per la comprovata affidabilità in strutture critiche.
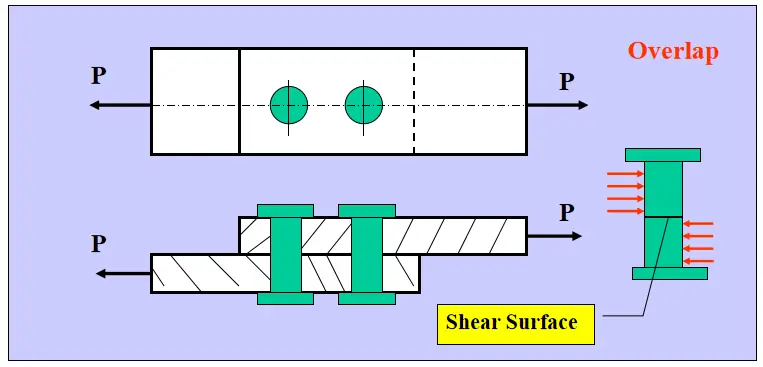
Giunto di testa a copertura singola
Giunto di testa a doppia copertura
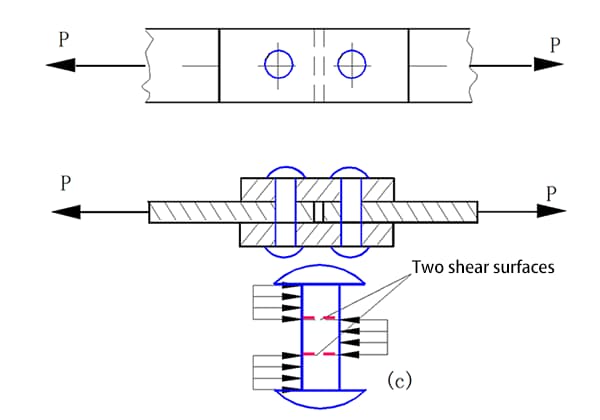
Carico laterale del gruppo di rivetti
Nel giunto rivettato (come mostrato nella figura precedente), per semplificare i calcoli, si assume che:
La formula per calcolare la forza che agisce su ciascun rivetto è:
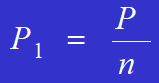
Esempio:
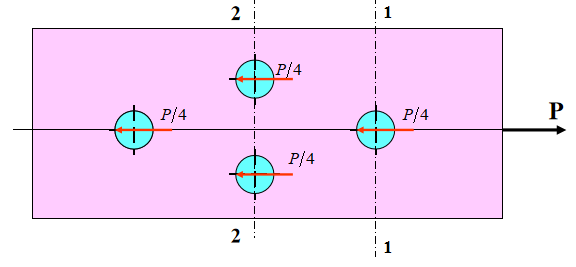
Per collegare due piastre d'acciaio si utilizza un giunto con quattro rivetti. Il materiale delle piastre d'acciaio e dei rivetti è lo stesso. Il diametro dei rivetti è d=16 mm, la dimensione dei rivetti è d=16 mm. lamiera d'acciaio è b=100mm, t=10mm, P=90KN, la tensione ammissibile dei rivetti è [τ]=120MPa, la tensione di snervamento ammissibile è [σjy]=120MPa, e la tensione di trazione ammissibile della piastra d'acciaio è [σ]=160MPa. Calcolare e verificare la resistenza del giunto rivettato.
(1) Resistenza al taglio dei rivetti:
La forza agente su ciascun rivetto è P/4.
La forza di taglio che agisce su ciascun rivetto è data da:
(2) Resistenza allo schiacciamento dei rivetti:
La forza che agisce su ciascun rivetto a causa dello schiacciamento è:
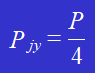
L'area del rivetto che viene schiacciata è:
(3) Resistenza alla trazione della lamiera d'acciaio
Domanda di riflessione:
Area della superficie di taglio del perno A.
Area della superficie di estrusione del perno Ajy.
Domanda supplementare:
Praticare un foro della forma mostrata nella figura su un Spessore 5 mm piastra d'acciaio. Se il limite di resistenza al taglio del materiale della piastra d'acciaio è 𝜏𝑏 = 300MPa, calcolare la forza di punzonatura F necessaria per la punzonatrice.
Soluzione: L'area della superficie di taglio è
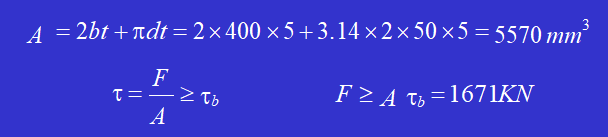
Domanda supplementare:
La forza massima di punzonatura di un punzonatrice è P = 400KN, la sollecitazione di compressione ammissibile [𝜎] della materiale del punzone è 440MPa e il limite di resistenza al taglio della piastra d'acciaio è 𝜏𝑏 = 360MPa. Determinare il diametro minimo d che il punzone può perforare e lo spessore massimo 𝜹 della piastra d'acciaio che può essere perforata.
Soluzione: Il punzone subisce una deformazione assiale di compressione.
In base alla condizione di rottura a taglio della piastra d'acciaio:
Esempio:
Utilizzando due binari in acciaio da rivettare in una trave composita, la situazione di collegamento è mostrata nelle figure a e b.
L'area della sezione trasversale di ogni guida d'acciaio A è di 8000 mm e il momento d'inerzia della sezione trasversale di ogni guida d'acciaio rispetto al proprio centroide è I = 1600 × 10 mm. La distanza tra i rivetti s è di 150 mm, il diametro d = 20 mm e la sollecitazione di taglio ammissibile [τ] è di 95 MPa. Se la forza di taglio interna Q della trave è di 50kN, verificare la resistenza al taglio dei rivetti. L'attrito tra la guida superiore e quella inferiore in acciaio non viene considerato.
Soluzione: Quando le due rotaie d'acciaio superiore e inferiore si piegano nel loro insieme, l'area della sezione trasversale della rotaia d'acciaio superiore è sottoposta a una sollecitazione di compressione, mentre l'area della sezione trasversale della rotaia d'acciaio inferiore è sottoposta a una sollecitazione di trazione.
A causa dei diversi momenti flettenti sulle sezioni trasversali adiacenti, lo sforzo normale nei punti corrispondenti è diverso, e quindi c'è una tendenza allo spostamento longitudinale lungo la superficie di contatto tra la rotaia superiore e quella inferiore in acciaio, facendo sì che i rivetti sopportino forze di taglio.
La forza di taglio sopportata da ogni fila di rivetti è pari alla differenza di forza di compressione (trazione) su due sezioni trasversali di una guida d'acciaio a una distanza longitudinale S.
Supponendo che le rotaie d'acciaio trasmettano la sollecitazione di taglio ovunque sulla superficie di contatto, la larghezza della superficie di contatto è b.
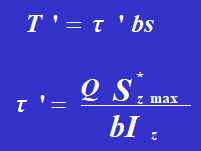
Szmax rappresenta il momento statico della sezione trasversale di una guida in acciaio rispetto all'asse neutro.
Iz è il momento d'inerzia dell'intera sezione trasversale rispetto all'asse neutro.
La sollecitazione di taglio del rivetto è:
La sollecitazione di taglio del rivetto soddisfa i criteri di resistenza.
Gruppo di rivetti sottoposto a carichi torsionali (vedi Figura).
Si consideri il centro della sezione trasversale del gruppo di rivetti come punto 0.
Assumendo che qualsiasi linea retta sulla piastra d'acciaio (come OA o OB) rimanga retta dopo la rotazione, la deformazione media a taglio di ciascun rivetto è proporzionale alla distanza dal centro della sezione trasversale del rivetto al punto O.
Se il diametro di ciascun rivetto è lo stesso, la forza su ciascun rivetto è proporzionale alla distanza dal centro della sezione trasversale del rivetto al centro della sezione O del gruppo di rivetti, con direzione perpendicolare alla linea che collega il punto e il centro O.
Pi rappresenta la forza che agisce su ciascun rivetto e ai rappresenta la distanza dal centro della sezione trasversale del rivetto dato al centro della sezione trasversale del gruppo di rivetti, indicata come O.
Il gruppo di rivetti sottoposto a carichi laterali eccentrici (vedi Figura a).
Semplificando il carico eccentrico P che agisce sul gruppo di rivetti al punto centrale O, si ottiene una forza P passante per il punto O e un momento m = Pe che ruota intorno al punto O.
Se il diametro di ciascun rivetto dello stesso gruppo di rivetti è lo stesso, è possibile calcolare la forza P1′ causata dalla forza laterale P e la forza P1" causata dal momento m. La forza che agisce su ciascun rivetto è la somma vettoriale di P1′ e P1". Dopo aver determinato la forza P1 su ciascun rivetto, è possibile verificare separatamente la resistenza al taglio e alla compressione del rivetto con la forza massima.
Esempio:
Una staffa collegata da un singolo rivetto è soggetta a una forza concentrata P, come mostrato nella Figura a. La forza esterna P è nota come 12 kN. Il diametro del rivetto è di 20 mm e ogni rivetto è soggetto a taglio singolo. Calcolare la massima sollecitazione di taglio sulla sezione trasversale del rivetto sotto la forza massima.
Soluzione:
Il gruppo di rivetti è simmetrico rispetto all'asse x e il centro di rotazione si trova nel punto O, che è il punto di intersezione della linea che collega il rivetto 2 e il rivetto 5 con l'asse x.
1. Semplificando la forza P verso il punto O, si ha:
P = 12 kN.
m=12 0,12=1,44KN.m
2. Sotto l'azione della forza P che passa per il centro di rotazione, e considerando che ogni rivetto ha lo stesso diametro e lo stesso materiale, la forza su ogni rivetto è uguale.
3. Sotto l'azione del momento m, la forza che ogni rivetto sopporta è proporzionale alla distanza del rivetto dal centro di rotazione.
Secondo l'equazione di bilancio:
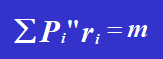
Risolvendo l'equazione, si ottiene:
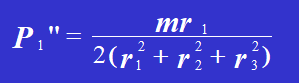
Pertanto,
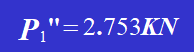
4. Disegnare il diagramma delle forze di ciascun rivetto e combinare i vettori Pi' e Pi" per ottenere la forza di taglio totale che agisce su ciascun rivetto, compresa la sua entità e direzione. Si può concludere che il rivetto 1 e il rivetto 6 sopportano la forza massima, con il valore della forza massima pari a:
La sollecitazione di taglio sulla sezione trasversale del rivetto è:
Di seguito sono riportate le risposte ad alcune domande frequenti:
In edilizia si utilizzano diversi tipi di rivetti per le loro proprietà e applicazioni uniche. I rivetti solidi, noti anche come rivetti tondi, sono il tipo più comune e più antico, costituito da un albero solido e da una testa. Vengono installati deformando la coda con un martello o un utensile a crimpare e sono ampiamente utilizzati per la loro elevata resistenza e affidabilità. I rivetti strutturali in acciaio sono simili ai rivetti pieni, ma sono progettati per applicazioni ad alta sollecitazione nell'edilizia commerciale, come ponti e grattacieli.
I rivetti ciechi, o rivetti a strappo, sono rivetti tubolari con un mandrino al centro, installati con una rivettatrice. Sono ideali per le applicazioni in cui l'accesso al lato posteriore del giunto è limitato. I rivetti a strappo, simili ai rivetti ciechi, non richiedono un attrezzo speciale per l'installazione e vengono inseriti in posizione con un martello; sono adatti per applicazioni in cui i fori non penetrano nell'intero pannello o blocco.
I rivetti a filo, o rivetti svasati, hanno teste e fori svasati che permettono loro di stare a filo con la superficie, riducendo la resistenza aerodinamica e fornendo una finitura superficiale liscia. I rivetti a spacco, o rivetti biforcati, sono caratterizzati da estremità affilate che si dividono in direzioni opposte quando vengono conficcate in un materiale, ideali per unire materiali morbidi come legno, plastica e pelle. I rivetti tubolari sono cavi con una testa a un'estremità e una coda all'altra, richiedono una forza minore per l'installazione e sono utilizzati in applicazioni in cui i materiali da fissare sono morbidi.
I rivetti sono realizzati in diversi materiali, tra cui acciaio inox, acciaio, alluminio, ottone e rame, ciascuno scelto in base ai requisiti specifici del progetto. Questi materiali offrono diverse caratteristiche di forza, resistenza alla corrosione e peso, rendendo i rivetti versatili per una vasta gamma di applicazioni edilizie.
Quando si confrontano le connessioni rivettate con quelle saldate, emergono diverse differenze e considerazioni chiave. I giunti saldati offrono generalmente una maggiore resistenza e capacità di carico rispetto ai giunti rivettati. Un buon giunto saldato può raggiungere il 100% della resistenza del materiale madre, mentre i giunti rivettati hanno una resistenza inferiore a causa della riduzione della sezione trasversale dovuta ai fori praticati per i rivetti.
In termini di progettazione e installazione, la saldatura è spesso più semplice e veloce, poiché non richiede fori preforati o parti aggiuntive come i rivetti. La rivettatura, invece, comporta la foratura, il fissaggio e l'appiattimento dei rivetti, il che la rende più lunga e laboriosa.
Le prestazioni in caso di vibrazioni e fatica differiscono tra i due metodi. I giunti rivettati resistono meglio ai carichi ciclici e alle vibrazioni perché la deformazione e l'espansione dei rivetti possono rafforzare la connessione nel tempo. I giunti saldati, pur essendo robusti, possono essere più suscettibili al degrado sotto cicli di carico ripetuti.
Per quanto riguarda i materiali e la compatibilità, la rivettatura è più versatile per unire materiali dissimili, poiché non richiede la considerazione dei punti di fusione. La saldatura, invece, richiede materiali con punti di fusione e proprietà termiche compatibili.
Dal punto di vista estetico, i giunti saldati possono offrire una finitura superficiale più liscia dopo la post-lavorazione, spesso più gradevole rispetto alle teste di rivetto visibili dei giunti rivettati.
Per quanto riguarda la manutenzione e lo smontaggio, i giunti rivettati sono più facili da smontare e riparare, poiché i rivetti possono essere forati e sostituiti. I giunti saldati sono più permanenti e richiedono il taglio e la risaldatura per lo smontaggio, che è più lungo e costoso.
In termini di peso e integrità strutturale, le strutture saldate sono in genere più leggere perché non richiedono materiali aggiuntivi come rivetti e cinghie. Le strutture rivettate possono essere più pesanti a causa di questi componenti aggiuntivi.
Anche i costi e l'efficienza giocano un ruolo nella scelta tra i due metodi. La rivettatura tende a essere complessivamente più costosa, nonostante il basso costo dei singoli rivetti, a causa dell'accumulo dei costi di materiale, di esercizio e di manodopera. La saldatura, soprattutto con processi automatizzati, può essere più economica e veloce.
In sintesi, la scelta tra rivettatura e saldatura dipende dai requisiti specifici dell'applicazione, tra cui le esigenze di resistenza, la compatibilità dei materiali, le considerazioni estetiche e i requisiti di manutenzione. La saldatura offre una maggiore resistenza, una progettazione più semplice e una produzione più rapida, ma può introdurre distorsioni termiche ed è meno flessibile per lo smontaggio. La rivettatura offre una migliore resistenza alle vibrazioni, una maggiore facilità di smontaggio e la possibilità di unire materiali dissimili, ma è generalmente più debole e richiede più lavoro.
I giunti rivettati sono ampiamente utilizzati nell'ingegneria moderna grazie alla loro durata, affidabilità e ai vantaggi specifici rispetto ad altri metodi di giunzione. Nell'industria aerospaziale, i giunti rivettati sono fondamentali per collegare componenti come i pannelli della fusoliera e le ali, dove le loro caratteristiche di leggerezza e alta resistenza sono essenziali per mantenere l'integrità strutturale riducendo al minimo il peso. Nella cantieristica navale, i giunti rivettati sono indispensabili per l'assemblaggio degli scafi e di altre parti fondamentali delle navi, offrendo resistenza alla pressione dell'acqua e alla corrosione, elementi fondamentali per garantire l'integrità della tenuta stagna e la sicurezza in acque agitate.
Nel settore delle costruzioni e delle infrastrutture, i giunti rivettati sono utilizzati in strutture come ponti, torri ed edifici. Questi giunti sono apprezzati per la loro capacità di distribuire uniformemente i carichi e fornire stabilità alle strutture di grandi dimensioni, rendendoli ideali per le applicazioni che richiedono un supporto robusto, come le travi e le capriate dei ponti. Per i recipienti a pressione e le caldaie, i giunti rivettati sono preferiti quando i processi termici come la saldatura non sono praticabili o quando i giunti devono resistere alle fluttuazioni di temperatura e alle vibrazioni.
Anche l'industria automobilistica e dei trasporti pubblici trae vantaggio dai giunti rivettati, in particolare nella produzione di carrozzerie di autobus e filobus. Questi giunti assicurano connessioni forti e affidabili, in grado di sopportare le sollecitazioni e le vibrazioni associate a questi veicoli. Inoltre, i giunti rivettati si trovano in prodotti di consumo come utensili da cucina e coltelli da tasca, dove la loro forza, la leggerezza e la resistenza alla corrosione sono vantaggiose.
In generale, i giunti rivettati sono favoriti in ambienti soggetti a vibrazioni o carichi dinamici, grazie alla loro resistenza all'allentamento nel tempo. Sono anche adatti per le industrie che subiscono fluttuazioni di temperatura, in quanto non richiedono calore per l'installazione e sono resistenti all'espansione termica. Inoltre, i giunti rivettati sono più facili da ispezionare e smontare rispetto ai giunti saldati, con minori danni alle parti interessate. Queste caratteristiche fanno dei giunti rivettati il metodo preferito in diversi settori critici e ad alte prestazioni.
Le connessioni rivettate offrono diversi vantaggi e svantaggi, che le rendono adatte a specifiche applicazioni mentre presentano delle difficoltà in altre.
I vantaggi dell'utilizzo di connessioni rivettate includono l'economicità, in quanto i rivetti sono poco costosi e non richiedono elettricità o materiali speciali, risparmiando sui costi dei materiali e dell'energia. La rivettatura aumenta anche la produzione, poiché in genere richiede meno attrezzature e preparazione rispetto alla saldatura, riducendo così il tempo e le risorse necessarie. Il processo genera residui di scarto minimi, migliorando l'efficienza. Le connessioni rivettate offrono flessibilità nella progettazione e sono più facili da ispezionare e mantenere; i rivetti usurati possono essere sostituiti rapidamente con un'attrezzatura minima. Sono versatili, in grado di unire metalli ferrosi e non ferrosi, nonché materiali non metallici come legno, plastica e lastre di amianto. La rivettatura è rispettosa dell'ambiente e dell'utente, non produce fumi o gas e quindi è più sicura per i lavoratori. Inoltre, le giunzioni rivettate offrono un'elevata resistenza al taglio e una buona resistenza alla fatica, adatte ad applicazioni soggette a vibrazioni e forze d'urto.
Tuttavia, le connessioni rivettate presentano anche degli svantaggi. Richiedono un maggiore impiego di manodopera, con diverse fasi come la realizzazione dei fori e l'installazione dei rivetti, che possono aumentare i costi della manodopera. I rivetti aggiungono peso alla struttura, che può essere significativo in strutture di grandi dimensioni e può influire sull'efficienza strutturale. I fori necessari per i rivetti possono indebolire le piastre metalliche, provocando una concentrazione di tensioni intorno ai fori, che potrebbe richiedere uno spessore aggiuntivo o la sovrapposizione di piastre per mantenere l'integrità strutturale. Dal punto di vista estetico, le connessioni rivettate sono più visibili e possono sporgere dalla struttura, riducendo il fascino visivo rispetto alle giunzioni saldate. La rivettatura può essere rumorosa durante l'installazione e può essere soggetta a corrosione se non viene sigillata correttamente, aumentando i costi di manutenzione nel tempo. I giunti rivettati possono non garantire una tenuta stagna o a prova di perdite, a meno che non si utilizzino rivetti caldi o sigillanti, il che può essere uno svantaggio in alcune applicazioni. Infine, anche se i rivetti possono essere sostituiti, il processo può essere macchinoso e rumoroso e la sostituzione dei rivetti durante la manutenzione può essere più impegnativa rispetto ad altri metodi di fissaggio come i bulloni.
In sintesi, le connessioni rivettate sono economiche e flessibili, ma comportano requisiti di manodopera più elevati, peso strutturale aggiuntivo, problemi di concentrazione delle tensioni e limitazioni estetiche. La scelta tra la rivettatura e altri metodi di giunzione dipende dai requisiti specifici del progetto.
Mantenere e riparare efficacemente i collegamenti rivettati comporta diversi passaggi cruciali per garantire l'integrità e la longevità della struttura. L'ispezione regolare è fondamentale; controllate i giunti rivettati per verificare la presenza di segni di usura, corrosione e affaticamento. Pulire periodicamente le connessioni per rimuovere eventuali detriti, sporco o sostanze corrosive che potrebbero compromettere il giunto. Per la pulizia delle pistole pneumatiche per rivetti utilizzate per la manutenzione, assicurarsi che i tubi dell'aria e i raccordi siano puliti, lubrificati e ispezionati a fondo per evitare malfunzionamenti.
Quando si tratta di riparazioni, iniziare a identificare eventuali difetti, come dimensioni errate dei rivetti o preparazione impropria dei fori. Se è necessario sostituire i rivetti, rimuoverli con attenzione forando la testa e usando un punteruolo per staccare il gambo senza danneggiare il materiale circostante. Sostituire sempre i rivetti con la misura e il tipo corretti, assicurandosi che le tecniche di installazione siano corrette per evitare problemi come teste inclinate o crepe.
Per riparazioni più estese si possono utilizzare tecniche specializzate come il bobbing, il frenching e la saldatura ad anello, in particolare per rivetti vecchi o fortemente danneggiati. È inoltre fondamentale affrontare qualsiasi potenziale corrosione sigillando adeguatamente i giunti, soprattutto quando sono coinvolti metalli dissimili, per prevenire la corrosione galvanica.
Assicurarsi che i giunti rivettati non siano sottoposti a fatica e vibrazioni eccessive, che possono portare al cedimento. Evitare una compressione eccessiva durante l'installazione per evitare vuoti o l'indurimento del metallo. Dopo le riparazioni, eseguire test e ispezioni approfondite per confermare l'integrità strutturale e la tenuta stagna dei giunti. Risolvere tempestivamente eventuali perdite con ulteriori interventi di calafataggio o di regolazione dei rivetti.
Seguendo queste linee guida per la manutenzione e la riparazione, è possibile mantenere nel tempo la resistenza, l'affidabilità e la sicurezza delle connessioni rivettate.
In qualità di fondatore di MachineMFG, ho dedicato oltre un decennio della mia carriera al settore della lavorazione dei metalli. La mia vasta esperienza mi ha permesso di diventare un esperto nei campi della fabbricazione di lamiere, della lavorazione, dell'ingegneria meccanica e delle macchine utensili per metalli. Penso, leggo e scrivo costantemente su questi argomenti, cercando di essere sempre all'avanguardia nel mio campo. Lasciate che le mie conoscenze e la mia esperienza siano una risorsa per la vostra azienda.
IT 
EN 
AR 
DE 
ES 
FR 
ID 
JA 
NL 
PT 
PT_BR 
RU 
KO 
TR