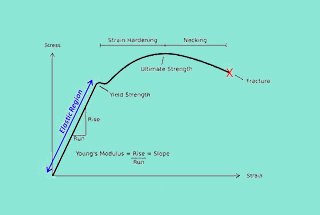
Vi siete mai chiesti perché gli alberi di trasmissione sono tipicamente circolari? Questo articolo approfondisce le ragioni meccaniche alla base di questa forma, spiegando come la sezione trasversale circolare ottimizzi le prestazioni torsionali e minimizzi le sollecitazioni. Scoprirete i vantaggi di questo design nel resistere alle deformazioni e nel garantire una trasmissione efficiente della potenza. Alla fine, capirete perché il design circolare è fondamentale per mantenere l'integrità meccanica in presenza di carichi variabili. Continuate a leggere per scoprire i principi ingegneristici che rendono l'albero di trasmissione circolare una scelta privilegiata nei sistemi meccanici.
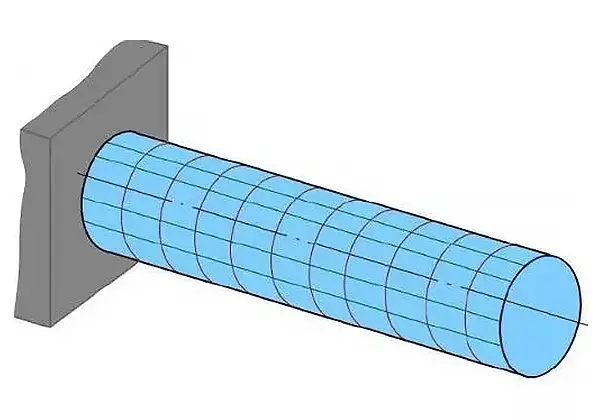
(1) Convenzione sui simboli di coppia
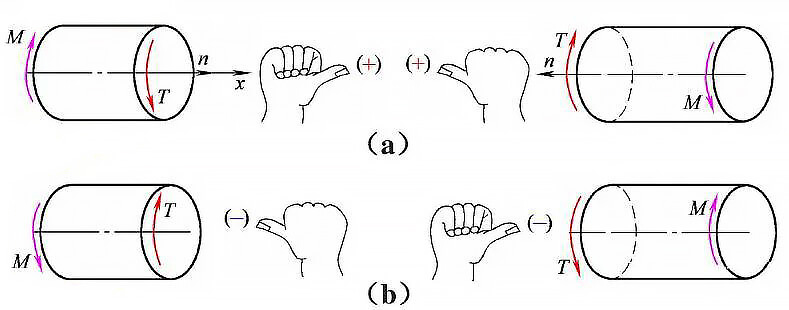
Fig. 1 direzione e simbolo della coppia
(2) Deformazione torsionale di una barra a sezione circolare
Dopo la torsione di un albero a sezione circolare, la forma e le dimensioni della sezione rimangono invariate e la sezione rimane piatta. Il raggio della sezione rimane l'asse attorno al quale la sezione viene attorcigliata e ogni sezione ruota solo di un piccolo angolo γ rispetto all'altra.
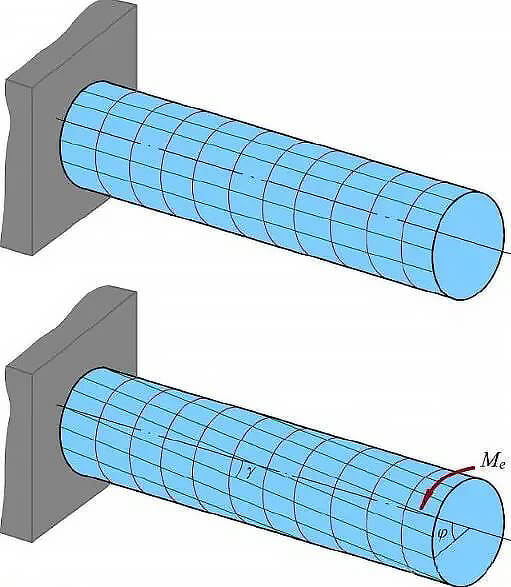
Fig. 2 deformazione torsionale di una barra a sezione circolare
(3) Torsione di una barra a sezione non circolare
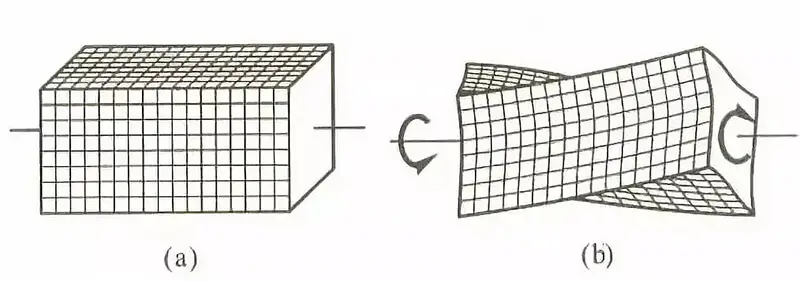
Fig. 3 deformazione torsionale di una barra quadrata
Torsione libera:
Quando una barra ha una sezione trasversale non circolare, si deforma durante la deformazione per torsione. Il grado di deformazione delle sezioni trasversali adiacenti sarà lo stesso, il che significa che la lunghezza di tutte le fibre longitudinali della barra non cambierà. In questo scenario, non ci sarà alcuna sollecitazione normale sulla sezione trasversale, ma solo una sollecitazione di taglio.
Per ottenere una torsione libera, le due estremità della barra diritta devono essere sottoposte a una coppia esterna e la deformazione delle sezioni adiacenti non deve essere vincolata esternamente.
Torsione vincolata:
Quando una barra diritta non uniforme viene attorcigliata, la quantità di coppia applicata cambia lungo la lunghezza della barra. Se un'estremità della barra è fissa e non può muoversi, il grado di deformazione delle sezioni adiacenti della barra sarà diverso. Oltre alla sollecitazione di taglio, si avrà anche una sollecitazione normale sulla sezione trasversale della barra.
Normalmente, lo sforzo normale causato dalla torsione vincolata in una barra solida è piccolo e può essere trascurato. Tuttavia, per le barre a parete sottile, questo sforzo normale è spesso troppo grande per essere ignorato.
(1) Ipotesi di piano
Dopo la torsione, la sezione circolare rimane piatta e la sua forma, dimensione e raggio rimangono invariati. Le sezioni ruotano l'una rispetto all'altra solo di un piccolo angolo γ. Tuttavia, questa ipotesi si applica solo all'asse della sezione circolare e non all'asse delle sezioni non circolari.
La distanza tra le sezioni adiacenti rimane la stessa, tranne quando τzx = τzy, che indica l'assenza di sforzo normale.
σ x= σ y= σ z= τ xy=0.
Il modello di elasticità è illustrato nella Fig. 4.

Fig. 4 Modello meccanico elastico a torsione di una barra diritta
(2) Manalogia con l'embrione
Prandtl sottolineò che l'abbassamento di un sottile film liquido, noto anche come membrana, sotto pressione uniforme è matematicamente simile alla funzione di sforzo nel problema della torsione di una barra rettilinea di sezione uguale.
Il confronto tra la barra di torsione e la membrana può essere utile per risolvere il problema della torsione.
Nella Figura 5, è presente un film uniforme teso su un confine orizzontale, che ha la stessa forma e dimensione del confine della sezione trasversale di una barra di torsione.
Quando si applica una piccola pressione uniforme alla pellicola, ogni punto della pellicola subisce una piccola flessione.
Se il piano in cui si trova il limite è il piano xy, la pendenza può essere rappresentata da z.
A causa della natura flessibile del film, si presume che non possa resistere al momento flettente, alla coppia, alla forza di taglio o alla pressione. Sopporta solo una forza di trazione uniforme FT, che è simile alla tensione superficiale di un film liquido.
Secondo questa analisi, la sollecitazione di taglio in qualsiasi punto della sezione trasversale della barra di torsione, lungo qualsiasi direzione, è uguale alla pendenza del film in direzione verticale in quel punto.
Si può osservare che la massima sollecitazione di taglio sulla sezione trasversale della barra di torsione è uguale alla massima pendenza della membrana. Tuttavia, va notato che la direzione della massima sollecitazione di taglio è perpendicolare alla direzione della massima pendenza.
In base a questa ipotesi, è possibile determinare la massima sollecitazione di taglio e l'angolo di torsione relativo della barra rettilinea a sezione non circolare elencata nella Tabella 1 di seguito.

Fig. 5 Modello di analogia della membrana
(1) Albero circolare pieno
In base alle ipotesi 1 e 2, le proprietà meccaniche dei materiali plastici nel taglio puro quando i materiali componenti sono all'interno dell'intervallo elastico:
τ= G γ,γ è la deformazione di taglio;
γ=φ R/L( γ è l'angolo di torsione relativo di due sezioni a una distanza L;
φ è l'angolo della faccia terminale dell'estremità di torsione, R è il raggio esterno del cerchio e L è la distanza tra due sezioni).

Fig. 6 Schema di torsione di una barra a sezione circolare piena
La sollecitazione di taglio a ρ sulla sezione circolare è:

Nella stessa condizione di coppia, la sollecitazione di taglio (τ) su una barra a sezione circolare è proporzionale alla distanza dal centro della sezione (ρ). Ciò significa che maggiore è la distanza dal centro, maggiore è la sollecitazione di taglio.
Quando la distanza dal centro è pari al raggio (R) della sezione circolare, la massima sollecitazione di taglio si ottiene sul bordo.
Il modulo di sezione torsionale (Wp) di un albero circolare può essere espresso come IP/R, dove IP è il momento d'inerzia polare. Questo valore è legato solo alle dimensioni geometriche della sezione e non all'area della sezione trasversale.
La sollecitazione di taglio massima (τ max) può essere calcolata come T/WP, dove T è la coppia applicata.
Per un albero solido a sezione circolare, il modulo di sezione torsionale (WP) è approssimativamente pari a 0,2 volte il cubo del diametro (D).
L'angolo di torsione (φ) di una barra circolare sottoposta a torsione è correlato alla rigidità torsionale (GIP) della sezione circolare, che riflette la capacità dell'albero di resistere alla deformazione.
Gli angoli di torsione relativi di due sezioni a una distanza L possono essere calcolati utilizzando una formula di torsione.
Angolo di torsione relativo:
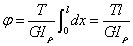
Condizione di rigidità dell'albero circolare:

(2) Albero circolare cavo
Il coefficiente torsionale di sezione dell'albero circolare cavo è circa: WP ≈ 0,2D3 (1- α 4),0< α= d/D<1.
Quando α= 0,8, il WP è pari a 60% della sezione circolare piena, ovvero, a parità di coppia, la resistenza diminuisce di 40%, ma a parità di materiale e lunghezza, la differenza di peso è di 2,8 volte.
(3) Tubo chiuso a parete sottile
Un tubo rotondo con uno spessore di parete (a) molto inferiore al suo raggio (R0) - tipicamente considerato ≤ R0/10 - è noto come tubo rotondo a parete sottile. Questo tipo di tubo può avere qualsiasi forma e sezione uguale.
Trattandosi di un tubo a parete sottile, si assume che la sollecitazione di taglio sia uniformemente distribuita lungo l'intero spessore della parete (t) per ottenere una soluzione approssimativa.
Applicando la regola della sollecitazione di taglio reciproca, si può concludere che il prodotto della sollecitazione di taglio assiale media di tutti i punti della sezione del tubo e della parete del tubo è uguale, cioè il flusso di taglio (q) è costante.
Poiché il valore di q è costante in tutta la sezione, la massima sollecitazione di taglio si trova in corrispondenza dello spessore minimo della parete.
Quando la sezione del tubo è circolare, la sua area (Am) è pari a πR0². L'aumento del diametro del cilindro può ridurre significativamente la sollecitazione di taglio.

Fig. 6 Distribuzione delle sollecitazioni di taglio di diverse sezioni comuni
Durante la prova di torsione, la distribuzione delle sollecitazioni sulla sezione trasversale del provino non è uniforme. La superficie subisce la maggior quantità di sollecitazioni, mentre man mano che ci si sposta verso il centro, le sollecitazioni si riducono.
Di conseguenza, quando il materiale viene sottoposto a torsione, il danno inizia dallo strato più esterno dell'asta rotonda e progredisce verso l'interno. La cricca inizia dallo strato superficiale e si propaga verso l'interno.
In ingegneria, la prova di torsione è comunemente utilizzata per esaminare i difetti superficiali e le prestazioni di un prodotto. indurimento superficiale strati nei materiali.
Come mostrato nella Fig. 7.

Fig. 7 prova di torsione del campione di barra tonda
Nel processo di torsione di un albero circolare realizzato in materiali plastici come l'acciaio a basso tenore di carbonio, la superficie dell'albero cederà per prima e poi la circonferenza verrà tagliata lungo la sezione con l'aumentare della deformazione torsionale.
Ciò è dovuto al fatto che la capacità di taglio del materiale è inferiore alla sua capacità di trazione e la massima sollecitazione di taglio si verifica sulla sezione trasversale, con conseguente rottura a taglio.
In ingegneria, la massima sollecitazione di taglio sul bordo esterno della sezione trasversale viene solitamente fissata al limite di snervamento a taglio del materiale (τs) come stato pericoloso, e la condizione di resistenza viene stabilita in base a questo.
Tuttavia, anche quando la sollecitazione di taglio sul bordo raggiunge il limite di snervamento, le altre parti si trovano ancora in uno stato di lavoro elastico lineare e l'asta rotonda non subisce un'evidente deformazione plastica, consentendo alla coppia di continuare ad aumentare.
Tenendo conto della plasticità del materiale, la coppia ultima (coppia plastica) di un tondino solido è 1/3 più grande della coppia di snervamento (che è il risultato di un calcolo ingegneristico semplificato).
Quando la sollecitazione di taglio sul bordo della sezione trasversale del materiale raggiunge il limite di snervamento a taglio del materiale τs, la regione plastica si espande gradualmente verso l'interno con l'aumento del momento di coppia torsionale e il materiale sul bordo della sezione trasversale inizia a rafforzarsi.
Se il momento di coppia torsionale continua ad aumentare, la cricca partirà dallo strato più esterno dell'asta rotonda e alla fine si taglierà lungo la sezione trasversale.
Come mostrato nella Fig. 8.

Fig. 8 prova di torsione di un campione di barra tonda in materiale plastico
Nel caso di un albero rotondo realizzato con materiali fragili, come la ghisa, con una capacità di trazione inferiore a quella di taglio, la deformazione durante la rottura torsionale è minima. L'albero tende a rompersi sulla superficie elicoidale con un angolo di circa 45° rispetto all'asse.
Questo perché il piano inclinato a 135° rispetto all'asse subisce la massima sollecitazione di trazione. Se la massima sollecitazione di trazione su questa sezione supera il limite di resistenza alla trazione del materiale, l'albero cede a causa della tensione su questa sezione.
Come mostrato nella Fig. 9.

Fig. 9 prova di torsione di un campione di tondo in materiale fragile
La coppia interna T ricevuta dall'asta del tronco non solo genera una distribuzione radiale lineare delle sollecitazioni di taglio sulla sezione trasversale, ma induce anche una corrispondente sollecitazione di taglio lungo il piano assiale, che può portare a cricche lungo il piano assiale.
Poiché il legno è un materiale anisotropo, la forza di taglio parallela alle fibre lungo la direzione assiale è molto più piccola della forza di taglio perpendicolare alle fibre nella sezione trasversale, con il risultato del modello di fessurazione rappresentato nella Figura 10.

Fig. 10 cedimento torsionale del tronco
La figura illustra le formule di calcolo per la sollecitazione massima e l'angolo di torsione di sezioni quadrate, triangolari ed ellittiche, secondo l'analisi della teoria dell'elasticità.
In tutti i casi citati, la massima sollecitazione di taglio si verifica in corrispondenza della linea di confine della sezione più vicina all'asse centrale.
Per un tubo chiuso a parete sottile, la posizione con lo spessore della parete più sottile rispetto all'asse centrale subisce la massima sollecitazione di taglio.

Fig. 11 formula di calcolo della sollecitazione di taglio torsionale e dell'angolo di torsione relativo di diverse sezioni
Sia S l'area di un cerchio, di un quadrato, di un triangolo e di un'ellisse, tutti soggetti alla stessa coppia T.
La lunghezza del lato di un quadrato è a = √S, mentre la lunghezza del lato di un triangolo equilatero è circa a ≈ 2,3√S.
Utilizzando la formula di calcolo della sollecitazione massima fornita nella figura, a parità di sezione trasversale e di coppia, la sollecitazione massima di taglio sulla sezione trasversale di un triangolo equilatero è circa 1,8 volte quella di un quadrato.
Per un'ellisse con a = b, che la rende un cerchio, a = 0,56√S, e la massima sollecitazione di taglio su un quadrato è circa 1,32 volte quella di un cerchio.
Se l'ellisse ha un ≠ b, con 1 > b/a = λ > 0, allora il rapporto tra la massima sollecitazione di taglio sull'ellisse e la massima sollecitazione di taglio sul cerchio è λ√S-2. Quindi, più piccolo è il valore di λ, maggiore è la sollecitazione di taglio. Pertanto, più piccolo è il valore di λ, maggiore è la sollecitazione di taglio.
Dal confronto di cui sopra, si può concludere che:
Quando un albero ha la stessa sezione e sopporta la stessa coppia, la sollecitazione di taglio massima sulla sezione circolare è minore rispetto alla sezione non circolare. Inoltre, anche l'angolo di torsione è minore. Pertanto, un albero di trasmissione circolare presenta un vantaggio naturale in termini di prestazioni meccaniche torsionali.
Estendendo questi risultati a sezioni trasversali arbitrarie, si può dimostrare che l'albero a sezione circolare ha la massima efficienza.
Quando un albero ha la stessa sezione e sopporta la stessa coppia, la sollecitazione di taglio massima sulla sezione circolare è minore rispetto alla sezione non circolare. Inoltre, anche l'angolo di torsione è minore. Pertanto, un albero di trasmissione circolare presenta un vantaggio naturale in termini di prestazioni meccaniche torsionali.
Estendendo questi risultati a sezioni trasversali arbitrarie, si può dimostrare che l'albero a sezione circolare ha la massima efficienza.
Tabella 1 formula di controllo della coppia del diametro dell'albero
|
Tipo di asse |
formula |
istruzione |
|
albero solido |
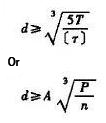 |
Dove: d - calcolare il diametro dell'albero alla sezione (mm) Coppia nominale T trasmessa dall'albero (N-mm) T=9550000P/n Potenza nominale P trasmessa dall'albero (kW) Velocità dell'albero n (R / min) [T] - sollecitazione di taglio ammissibile dell'albero (MPa)) A - coefficiente determinato da [t], Rapporto V tra il diametro interno d0 e il diametro esterno D dell'albero cavo circolare |
|
asse cavo |
 |
La sollecitazione di taglio superficiale di un albero a sezione circolare è elevata e il centro è relativamente piccolo quando sopporta un carico torsionale. Pertanto, la rimozione di parte del materiale che non svolge un ruolo completo nel centro può ridurre efficacemente il peso dell'albero e migliorarne la resistenza alla flessione.
Tuttavia, per decidere se rendere cave o meno le parti dell'albero è necessario considerare non solo i fattori meccanici, ma anche i costi tecnologici e di produzione. È importante notare che lo spessore della parete non deve essere troppo sottile, altrimenti si possono verificare pieghe locali, con conseguente perdita di capacità portante.
Quando lo spessore della parete (δ) del cilindro è molto più piccolo del raggio (R0), che generalmente è considerato ≤ R0/10, si parla di cilindro a parete sottile. Tuttavia, se il tubo a parete sottile presenta un'apertura longitudinale lungo l'asse, la sua resistenza alla torsione diminuisce notevolmente. Pertanto, di solito viene aggiunto un diaframma per migliorare la resistenza torsionale. rigidità e resistenza.
Un albero è tipicamente composto da varie sezioni e la concentrazione di tensioni nella posizione di transizione tra queste sezioni è una causa comune di rottura nelle parti dell'albero.
Per la scelta e la determinazione del diametro maggiore di due sezioni adiacenti e del filetto di transizione si può fare riferimento alla letteratura.
La molla a spirale cilindrica è un componente comune nell'ingegneria meccanica, caratterizzato da un asse a spirale e da una grande deformazione elastica.
Nella progettazione di una molla con un'elevata capacità di carico, la resistenza è in genere il fattore principale da considerare. Tuttavia, per una molla con una bassa capacità di carico, la deformazione è generalmente il fattore principale da considerare.
Per le molle meno critiche, la scelta può basarsi esclusivamente sulle dimensioni e sulle specifiche strutturali.
Per informazioni sui metodi di progettazione e calcolo delle molle, si rimanda alla letteratura in materia e alle norme della serie GB/T1239, GB/T2089, DIN2089 e altre norme applicabili.
Sotto l'azione di un carico statico, esiste una certa relazione tra le proprietà meccaniche dei materiali in torsione e in trazione, per cui [σ] dei materiali viene utilizzato per determinare la sollecitazione di taglio ammissibile[ τ]:.
| Tipo di materiale | [σ] | [ τ] | [ τ] |
| materiale plastico | 1 | 0.5~0.7 [σ] | 0,55 o 0,577 [σ] |
| Materiale fragile | 1 | 0.7~1.0 [σ] | 0.8~1.0 [σ] |
La tabella precedente evidenzia che la relazione tra sforzo di taglio e sforzo normale fornita in letteratura è diversa.
Diversi materiali plastici citati in letteratura mostrano che il rapporto tra sforzo di taglio e sforzo normale dovrebbe essere compreso tra 0,5 e 0,7 [σ].
Tuttavia, questa relazione è una stima approssimativa e deve essere utilizzata solo quando non sono disponibili i dati esatti sulla sollecitazione di taglio.
Per una verifica precisa, è necessario ottenere il valore della resistenza torsionale specifica del materiale.