Avete mai avuto difficoltà a dispiegare con precisione i pezzi di lamiera? Questo articolo esplora l'arte e la scienza che stanno alla base dei calcoli per lo svolgimento delle lamiere. Scoprite i concetti chiave, le formule e le tecniche utilizzate da ingegneri esperti per svolgere con precisione geometrie complesse. Imparate ad applicare questi principi ai vostri progetti e a semplificare il vostro processo di produzione.
La prima fase del processo di fabbricazione della lamiera è lo svolgimento delle geometrie e del corpo coerente. L'accuratezza e la correttezza dello svolgimento del campione influiscono direttamente sulla qualità del pezzo finale.
In passato, a causa delle limitazioni degli strumenti di calcolo, si utilizzava il metodo della proiezione per ingrandire il campione su un piano con un rapporto 1:1 e misurare la lunghezza reale della linea di pianta richiesta.
Tuttavia, questo metodo è complicato e inefficiente e non può soddisfare le attuali esigenze di produzione.
Con il progresso degli strumenti di calcolo, come le calcolatrici elettroniche e l'uso diffuso dei computer, lamiera è ora possibile eseguire il dispiegamento con metodi di calcolo.
Per standardizzare il metodo di calcolo del coefficiente di piegatura della lamiera da parte dei tecnici, ridurre al minimo le deviazioni dimensionali dei prodotti dopo la piegatura e facilitare l'autoispezione da parte del personale dell'officina e la ripetizione dell'ispezione da parte degli ispettori di qualità, è stato definito uno standard unificato e una base per il coefficiente di piegatura.
Di conseguenza, lo standard di calcolo per il coefficiente di piegatura della lamiera è diventato sempre più standardizzato.
Metodo di dispiegamento dello strato neutro
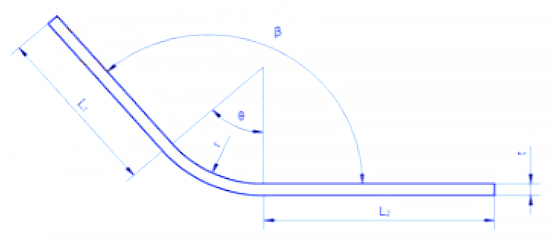
Nel processo di flessione, lo strato esterno subisce una sollecitazione di trazione, mentre lo strato interno subisce una sollecitazione di compressione. Lo strato di transizione tra le sollecitazioni di trazione e di compressione viene definito strato neutro. La lunghezza dello strato neutro durante la piegatura rimane la stessa di quella prima della piegatura, e quindi è il punto di riferimento per determinare la lunghezza non piegata del pezzo piegato.
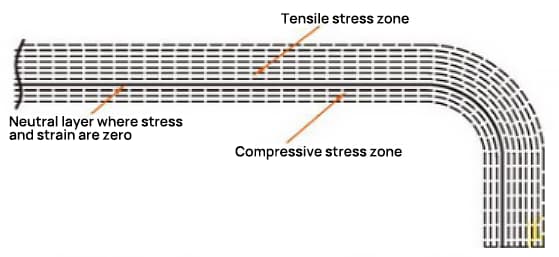
La posizione dello strato neutro dipende dal grado di deformazione.
La posizione dello strato neutro non è legata solo al raggio di curvatura, allo spessore della lamiera, al coefficiente di spostamento verso l'interno, ecc. ma anche a fattori quali il metodo di lavorazione, la forma e le dimensioni della lamiera.
Pertanto, la posizione dello strato neutro può essere determinata solo in modo approssimativo e, nelle applicazioni pratiche, per il calcolo si utilizzano generalmente valori approssimativi.
La formula di calcolo per la dimensione della lunghezza L dello strato neutro è la seguente:
Tra questi,
Utilizzando un software 3D per eseguire simulazioni e calcoli di vari spessori, angoli e raggi, insieme alle pratiche di fabbricazione in loco, abbiamo compilato una serie di valori di fattore K. Per i valori specifici si rimanda alla Tabella 1.
Tabella 1: Valori del coefficiente K dello strato neutro
| r/t | ≤05 | 0.6 | 0.8 | 1 | 1.2 | 1.3 | 1.5 | 2 | 2.5 | 3.0 | 4.0 | 5.0 | 6.0 | ≥8 |
| k | 026 | 0.28 | 0.30 | 0.32 | 0.33 | 0.34 | 0.36 | 0.38 | 0.39 | 0.4 | 0.42 | 0.44 | 0.46 | 0.5 |
Calcolo del dispiegamento rapido per curve a 90°
Il diagramma di piegatura per una curva a 90° è illustrato nella Figura 9. Negli ultimi anni, abbiamo utilizzato software 3D come CATIA e SOLIDWORKS per la modellazione della lamiera per calcolare le dimensioni di piegatura.
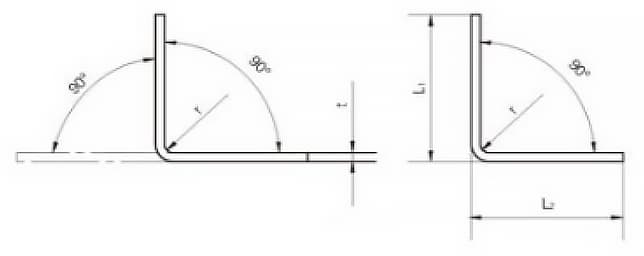
Attraverso ripetute verifiche, si è osservato che quando l'angolo di piegatura a freddo dei prodotti piatti in acciaio è di 90°, la formula per calcolare la lunghezza di piegatura L è la seguente:
L = L1 + L2 - A
Dove,
Tabella 2 Tabella dei parametri di piegatura a 90°
| Spessore t/mm | Raggio di allettamento r/mm | |||||||||||
| 1 | 1.2 | 16 | 2 | 25 | 3 | 4 | 5 | 6 | 8 | 10 | 12 | |
| Valore di compensazione A mm | ||||||||||||
| 1 | -1.92 | -1.97 | -2.10 | -2.23 | -2.41 | -2.59 | -2.97 | -3.36 | -3.79 | -4.65 | -5.51 | -6.37 |
| 1.5 | -2.90 | -3.02 | -3.18 | -3.34 | -3.70 | -4.07 | -4.45 | -5.26 | -6.11 | -6.97 | ||
| 2 | -3.84 | -3.98 | -4.13 | -4.46 | -4.81 | -5.18 | -5.94 | -6.72 | -7.58 | |||
| 2.5 | -4.80 | -4.93 | -5.24 | -5.57 | -5.93 | -6.66 | -7.42 | -8.21 | ||||
| 3 | -5.76 | 6.04 | -6.35 | -6.69 | -7.40 | -8.14 | -8.91 | |||||
| 4 | -7.7 | -7.95 | -8.26 | -8.92 | -9.62 | -10.36 | ||||||
| 5 | -9.6 | -9.87 | -10.48 | -11.15 | -11.85 | |||||||
| 6 | -11.5 | -12.08 | -12.71 | -13.38 | ||||||||
| 8 | -15.4 | -15.9 | -16.51 | |||||||||
| 10 | -19.2 | -19.73 | ||||||||||
| 12 | 23.01 | |||||||||||
Quando il raggio di curvatura è grande e l'angolo di flessione è piccolo, il grado di deformazione è basso e lo strato neutro è vicino al centro dello spessore della lastra.
Tuttavia, quando il raggio di curvatura (R) diventa più piccolo e il angolo di curvatura (θ) aumenta, aumenta anche il grado di deformazione e lo strato neutro si sposta verso il lato interno del centro di flessione. La distanza dallo strato neutro al lato interno della lastra è indicata con λ, mentre lo spessore del materiale è indicato con T.
La formula di base per il calcolo della lunghezza di svolgimento:
Lunghezza di svolgimento = dimensione interna del materiale + dimensione interna del materiale + quantità di compensazione.
È inoltre possibile utilizzare la seguente calcolatrice per calcolare la lunghezza di svolgimento della lamiera:

Di seguito vengono descritti uno per uno gli algoritmi di dispiegamento delle varie caratteristiche di curvatura.
R = 0 mm, θ = 90° (Nota: quando R ≤ 1,0 mm, viene considerato come R = 0 mm).
L = A + B + K
Nella produzione reale, lo stampo superiore di piegatura può presentare un angolo R, oppure può esserci un angolo R inferiore a 1 mm, o ancora la scelta della stampo inferioreLa fessura V della piastra può essere grande, tra le altre ragioni, e ciò comporta un coefficiente di flessione ridotto. Di conseguenza, il coefficiente di flessione dello spessore di ciascuna piastra di materiale è presentato nella Tabella 1 in base a valori empirici reali.
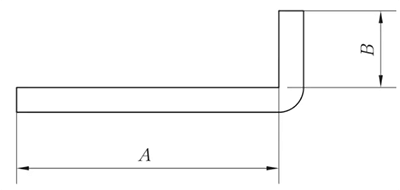
Fig. 1 Schema generale della flessione I
R ≠ 0mm e θ = 90°
L = A + B + K (K è la lunghezza dell'arco dello strato neutro)
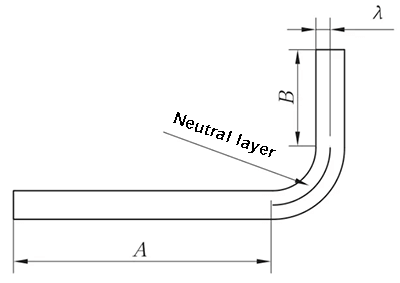
Fig. 2 Schema di flessione generale II
R = 0 mm, θ ≠ 90°
L = A + B + K'
Nota: K è la quantità di compensazione a 90°.
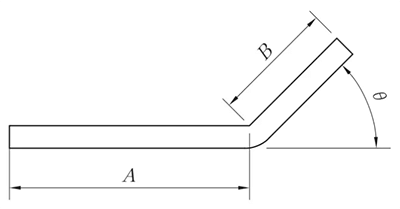
R ≠ 0mm, θ ≠ 90°
L = A + B + K
(K prende la lunghezza dell'arco dello strato neutro)
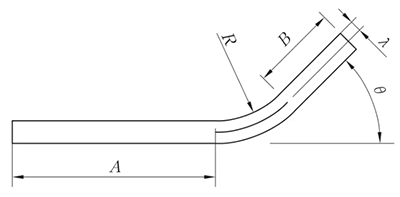
Fig. 4 Curvatura generale IV diagramma di piegatura
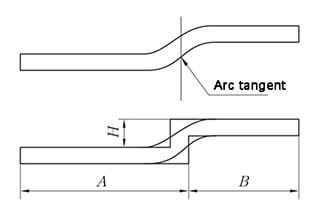
Il metodo di dispiegamento è equivalente al metodo di piegatura a Z con bordi dritti paralleli e la misura dell'altezza è illustrata nella Figura 6.
L'angolo θ è considerato un dispiegamento di 90°.
Per 0 < T ≤ 1,6 mm, λ è uguale a 0,5T.
Quando T è superiore a 1,6 mm, λ è uguale a 0,4T.
Piegatura a Z, detta anche Curvatura offset, si distingue in curvatura offset con bordo dritto e curvatura offset con bordo smussato in base all'angolo di formatura e il metodo di lavorazione è determinato dall'altezza di offset.
Quando l'altezza di offset, h, è inferiore a 3,5 volte lo spessore del materiale, matrici offset per la formatura si utilizzano stampi a cambio di matrice.
Se l'altezza di offset supera 3,5 volte lo spessore del materiale, si ricorre alla normale formatura positiva e negativa.
Quando la lunghezza del bordo smussato è inferiore a 3,5 volte lo spessore del materiale, per la formatura si utilizzano stampi offset o stampi intercambiabili.
Se la lunghezza del bordo smussato supera 3,5 volte lo spessore del materiale, si applica la normale piegatura uno-positiva e uno-negativa.
(1) Quando H < 3,5T, solo in questo caso può essere elaborato mediante piegatura offset.
L = A + B + H
(se H ≤ T, compensare 0,2 mm)
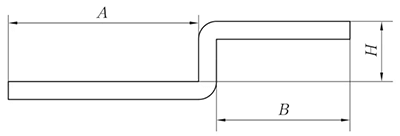
Fig. 5 Schema dello spostamento del bordo rettilineo
(2) Sfalsamento del bordo dritto non parallelo
Il metodo di espansione è lo stesso del metodo di piegatura a Z con bordo rettilineo parallelo, e il valore dell'altezza è mostrato nella Figura 6.
L'angolo θ può essere considerato come un angolo di 90° non piegato.
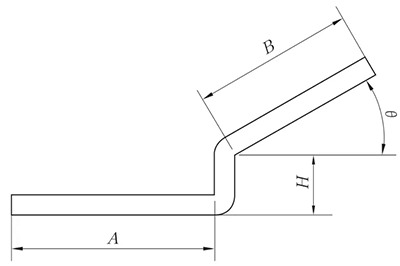
Fig. 6 Schema del disassamento del bordo rettilineo non parallelo
(3) Sfalsamento del bordo rettilineo - il segmento di transizione è tangente a due archi
Quando il sistema Straight-Edge Offset viene dispiegato nel punto di tangenza di due archi circolari, si crea una linea verticale nel punto di tangenza dei due archi circolari sulla superficie esterna del substrato. Il materiale viene quindi spostato di uno spessore verso l'interno, come illustrato nella Figura 7, per essere lavorato e dispiegato con il metodo Z-Fold 1 (Straight-Edge Offset).
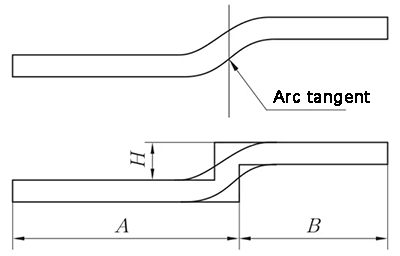
Fig. 7 Diagramma di sfalsamento del bordo rettilineo - il segmento di transizione è tangente a due archi circolari
Quando H < 2T, l'algoritmo di dispiegamento è il seguente, in base all'elaborazione dell'offset.
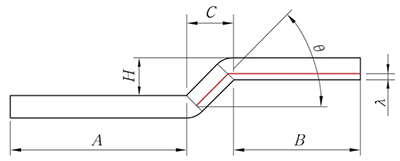
Fig. 8 Schema di sfalsamento del bordo smussato
L = A + B - K
(1) Quando si appiattisce, considerare la possibilità di pressare la linea prima della piegatura in base alle condizioni effettive.
La posizione di pressatura della linea è al centro dell'area di deformazione da flessione.
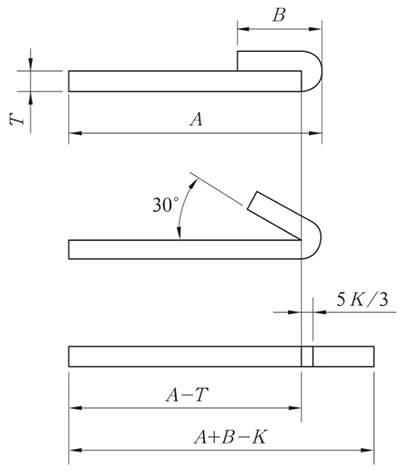
Fig. 9 Schema della piegatura e dell'appiattimento inverso
I processi di piegatura e appiattimento inverso vengono solitamente eseguiti in due fasi: prima il materiale viene piegato a 30° utilizzando la matrice di inserimento, quindi viene appiattito.
Pertanto, quando si crea il file linea di piegatura sul disegno esteso, è essenziale illustrare la linea di piegatura basata sulla piegatura a 150°, come dimostrato nella Figura 9.
Tabella 1 Coefficiente di flessione di piastre di diverso spessore con diversi angoli di flessione
| Angolo | Spessore/mm | ||||
|---|---|---|---|---|---|
| 1 | 1.2 | 1.5 | 1.8 | 2.5 | |
| 45° | 5.3 | 6.3 | 7.8 | 9.5 | 13 |
| 50° | 4.5 | 5.4 | 6.8 | 8.1 | 11.25 |
| 55° | 4 | 4.7 | 5.8 | 7.05 | 9.75 |
| 60° | 3.4 | 4.1 | 5.1 | 6.15 | 8.5 |
| 65° | 3 | 3.6 | 4.5 | 5.4 | 7.5 |
| 70° | 2.65 | 3.2 | 4 | 4.75 | 6.6 |
| 75° | 2.35 | 2.8 | 3.5 | 4.25 | 5.9 |
| 80° | 2.1 | 2.5 | 3.1 | 3.75 | 5.25 |
| 85° | 1.9 | 2.25 | 2.8 | 3.35 | 4.65 |
| 90° | 1.7 | 2 | 2.5 | 3 | 4.15 |
| 95° | 1.5 | 1.8 | 2.2 | 2.7 | 3.75 |
| 100° | 1.35 | 1.6 | 2 | 2.4 | 3.35 |
| 105° | 1.2 | 1.4 | 1.75 | 2.15 | 3 |
| 110° | 1.1 | 1.3 | 1.6 | 2 | 2.65 |
| 115° | 1 | 1.25 | 1.4 | 1.7 | 2.35 |
| 120° | 0.85 | 1 | 1.25 | 1.5 | 2.1 |
| 125° | 0.75 | 0.9 | 1.1 | 1.35 | 1.85 |
| 130° | 0.65 | 0.8 | 1 | 1.18 | 1.65 |
| 135° | 0.55 | 0.7 | 0.85 | 1.05 | 1.45 |
| 140° | 0.5 | 0.6 | 0.75 | 0.9 | 1.25 |
| 145° | 0.43 | 0.5 | 0.65 | 0.77 | 1.05 |
| 150° | 0.35 | 0.43 | 0.55 | 0.65 | 0.9 |
| 155° | 0.3 | 0.35 | 0.45 | 0.53 | 0.75 |
| 160° | 0.23 | 0.27 | 0.35 | 0.4 | 0.6 |
| 165° | 0.17 | 0.2 | 0.25 | 0.3 | 0.45 |
Il metodo di elaborazione N-fold prevede sia il rimodellamento che l'appiattimento, e l'algoritmo per il dispiegamento è:
L = A + B + K
(K prende la lunghezza dell'arco dello strato neutro).
λ = 0,5T
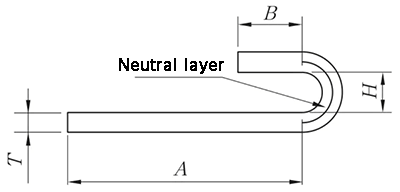
Fig.10 Diagramma a N
(1) L'espansione dell'arco è direttamente K e viene presa la lunghezza dell'arco dello strato neutro. λ= 0,5T
(2) Espansione con il bordo dritto su un lato.
L = A + K
(k è la lunghezza dell'arco dello strato neutro)
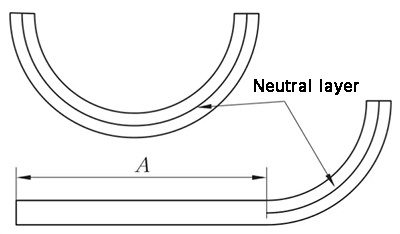
Fig. 11 Schema di piegatura ad arco
Nella produzione reale, il controllo preciso della lunghezza della lamiera dispiegata attraverso il software 3D può essere ottenuto principalmente attraverso i seguenti passaggi e metodi:
Scegliete il giusto software di progettazione 3D: Innanzitutto, è necessario scegliere un software CAD 3D adatto alla progettazione di lamiere. SolidEdge, Creo, FreeCAD, UG, ecc. sono tutti software che possono essere utilizzati per la progettazione di lamiere. Questi software offrono moduli per la lamiera o funzioni correlate che possono aiutare i progettisti nella progettazione e nel calcolo dello sviluppo di parti in lamiera.
Utilizzare il modulo lamiera o gli strumenti del software: La maggior parte dei software CAD 3D offre strumenti e funzioni correlate per la progettazione di lamiere. Ad esempio, Creo offre una serie di metodi per il controllo delle dimensioni della lamiera dispiegata, tra cui i metodi di modellazione e dispiegamento di parti di lamiera ad arco ampio, il metodo di deduzione delle piegature, ecc. Anche FreeCAD, un software di modellazione 3D open-source, offre un modulo per la lamiera.
Appmetodi di calcolo che si dispiegano: Per garantire l'accuratezza della lunghezza dopo lo svolgimento della lamiera, è possibile utilizzare diversi metodi di calcolo dello svolgimento. I metodi più comuni sono il metodo di compensazione della piegatura, il metodo di deduzione della piegatura e il metodo di calcolo del fattore K. Questi metodi possono aiutare i progettisti a calcolare la lunghezza effettiva del materiale allo stato spiegato, garantendo così le dimensioni previste. Questi metodi possono aiutare i progettisti a calcolare la lunghezza effettiva del materiale allo stato non piegato, garantendo così le dimensioni previste dei pezzi dopo la piegatura e la formatura finale.
Prestare attenzione alla gestione dei bordi e degli angoli e alla regolazione dei dettagli: Nel processo di progettazione della lamiera, i dettagli della gestione dei bordi e degli angoli sono molto importanti. Alcuni software, come SW, offrono una serie di soluzioni per la gestione dei bordi e degli angoli e metodi di piegatura, che aiutano a migliorare la precisione di piegatura.
Per le curve non a 90 gradi, gli angoli di piega più comuni includono, ma non solo, 45 gradi e 135 gradi. Il metodo di calcolo del fattore K si basa sul rapporto tra lo spessore del materiale e il raggio di curvatura.
In particolare, il fattore K = δ / T, dove δ rappresenta lo spessore del materiale e T il raggio di curvatura. Questo metodo è applicabile per calcolare il coefficiente di curvatura di qualsiasi angolo non di 90 gradi.
Nelle applicazioni pratiche, a causa delle possibili differenze e dei grandi errori nei valori di deduzione delle curve con angoli diversi, il fattore K viene generalmente utilizzato come coefficiente di curvatura.
Inoltre, per guidare con precisione il valore del fattore K di diversi spessori di lamiera, sono necessari degli aggiustamenti. Alcuni riferimenti suggeriscono che il valore del fattore K per qualsiasi raggio di curvatura può essere calcolato attraverso specifiche tecniche di interpolazione, che si sono dimostrate efficaci per le applicazioni industriali della lamiera.
La formula di calcolo per la lunghezza espansa della lamiera pressopiegata smussata è: [L = A + B + C + 0,2], dove (A), (B) e (C) rappresentano le dimensioni interne e 0,2 serve come valore di compensazione.
Basato sui principi generali e sulle pratiche di calcolo dell'espansione della lamiera, questo valore di compensazione tiene conto delle discrepanze tra le lunghezze effettive e quelle calcolate teoricamente, dovute a fattori quali la piegatura del materiale e gli errori di precisione dello stampo durante le operazioni reali.
Nella lavorazione della lamiera, questo valore di compensazione contribuisce a garantire la precisione dimensionale e la qualità del prodotto finale.
Le parti in lamiera sono ampiamente utilizzate nei settori elettromeccanico, dell'industria leggera e automobilistico.
La forma dispiegata delle parti in lamiera è il principale fattore determinante per le dimensioni dello spezzone, che a sua volta influisce sulle dimensioni e sulla forma dello spezzone.
Tuttavia, i metodi tradizionali di piegatura dei pezzi di lamiera sono diventati sempre più inadeguati a soddisfare le moderne esigenze di progettazione a causa dei loro cicli lunghi, della bassa efficienza e della scarsa qualità.
Per ovviare a queste carenze, negli ultimi anni si è diffuso sempre più l'uso di sistemi CAD avanzati.
Questi sistemi specializzati nella progettazione di parti in lamiera vantano solide funzionalità e possono ridurre notevolmente il tempo e lo sforzo necessari per la progettazione preliminare e la realizzazione di parti in lamiera.