Come si misura la rettilineità di una guida per garantire la precisione delle operazioni in macchina? Questo articolo analizza due metodi comuni: il metodo di collegamento dei due punti di estremità e il metodo delle condizioni minime. Confrontando queste tecniche, imparerete come ognuna di esse valuta gli errori di rettilineità e perché la scelta del metodo giusto è fondamentale per ottenere misure accurate. Immergetevi per capire i pro e i contro di ciascun approccio e scoprite quale metodo è più adatto alle vostre esigenze per ottenere una rettilineità ottimale nei vostri progetti di ingegneria.
Nella pratica ingegneristica, esistono due metodi comunemente utilizzati per valutare l'errore di rettilineità delle rotaie di guida: il metodo del collegamento a due punti di estremità e il metodo delle condizioni minime.
Il metodo di connessione a due punti finali collega la curva di errore da un capo all'altro, quindi traccia due linee parallele alla linea da un capo all'altro nei punti più alti e più bassi della curva e misura i valori lungo l'asse verticale tra le due linee parallele.
Dopo l'elaborazione dei dati, il valore è l'errore di rettilineità della guida.
Il metodo delle condizioni minime collega i punti "alto, alto" (o "basso, basso") della curva di errore e traccia una linea parallela ad essa attraverso il punto basso (alto).
Il valore misurato tra le due linee parallele lungo l'asse verticale è l'errore di rettilineità della guida dopo l'elaborazione dei dati.
Il metodo delle condizioni minime è una valutazione arbitrale.
Il metodo di connessione a due punti finali non è una valutazione arbitrale, ma è comunemente utilizzato in produzione per la sua semplicità e convenienza nella valutazione, anche se a volte può produrre grandi errori.
Questo articolo discute il valore limite dell'errore generato tra questi due metodi di valutazione.
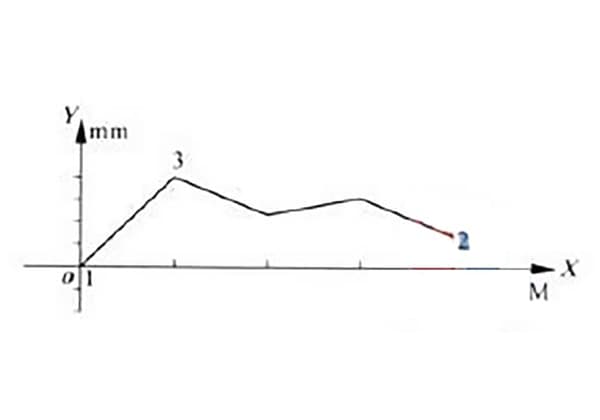
Misurando l'errore di rettilineità di un determinato modello di guida idraulica a scorrimento, si è ottenuta la curva dell'errore di rettilineità riportata nella Figura 1.
Come si può vedere dalla figura, la curva di errore si trova sullo stesso lato di entrambe le estremità della linea.
Di seguito, il valore dell'errore di rettilineità della rotaia di guida sarà valutato utilizzando il metodo delle condizioni minime e il metodo del collegamento a due estremità.
(1) Valutazione dell'errore di rettilineità con il metodo delle condizioni minime
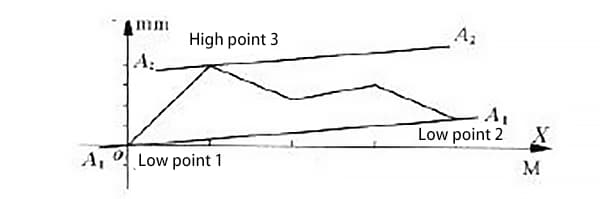
Secondo il metodo delle condizioni minime, i punti più bassi 1 e 2 della curva di Figura 1 (con il punto più basso 1 che coincide con l'origine) sono collegati dalla retta a1a1, come mostrato in Figura 2.
La retta parallela a2a2 passa per il punto più alto 3 rispetto alla retta a1a1.
Il valore misurato lungo l'asse y nella regione racchiusa dalle due rette parallele a1a1 e a2a2, dopo l'elaborazione dei dati, rappresenta l'errore di rettilineità della guida δ ottenuto con il metodo delle condizioni minime.
(2) Valutazione dell'errore di rettilineità con il metodo del collegamento a due estremità
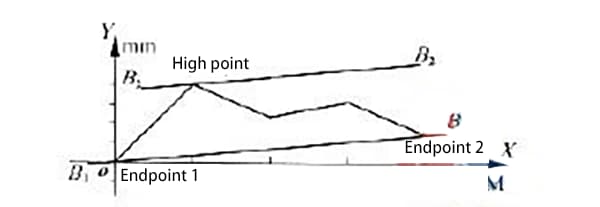
Secondo il metodo di connessione a due estremità, le estremità della curva nella Figura 1 sono anche i punti finali 1 e 2 della curva, come mostrato nella Figura 3.
I punti finali 1 e 2 sono collegati dalla retta b1b1, quindi si traccia una retta parallela b2b2 passante per il punto più alto.
Il valore misurato lungo l'asse y nella regione racchiusa dalle due rette parallele b1b1 e b2b2, dopo l'elaborazione dei dati, rappresenta l'errore di rettilineità della guida δ ottenuto con il metodo del collegamento a due estremità.
(3) Determinazione del limite di errore generato dai due metodi di valutazione
Poiché entrambi i metodi di valutazione vengono utilizzati per determinare l'errore di rettilineità della stessa rotaia di guida, il "punto basso 1", il "punto basso 2" e il "punto alto 3" della Figura 2 corrispondono rispettivamente al "punto finale 1", al "punto finale 2" e al "punto alto 3" della Figura 3. Ciò fa sì che la linea a1a1 coincida con la linea b1b1 e la linea a2a2 con la linea b2b2. In questo modo la linea a1a1 coincide con la linea b1b1 e la linea a2a2 coincide con la linea b2b2.
Pertanto, il valore dell'errore generato dai due metodi di valutazione è pari a zero.
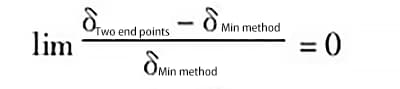
In base all'analisi precedente, quando la curva di errore si trova sullo stesso lato di entrambe le estremità della linea, il limite di errore generato dai due metodi di valutazione è pari a zero, il che significa che i risultati di valutazione ottenuti dai due metodi sono uguali.
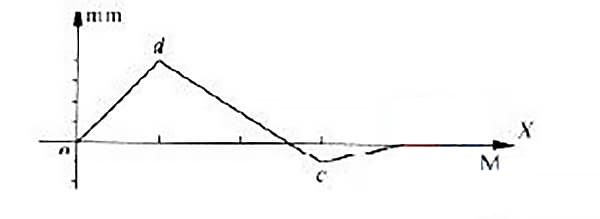
Nella curva di errore di rettilineità misurata di una guida, alcune curve di errore si trovano su entrambi i lati della linea che collega le estremità, come illustrato nella Figura 4.
La curva di errore di questa rotaia di guida ha una linea che collega le sue estremità coincidenti con l'asse delle ascisse. L'errore di rettilineità della guida sarà valutato con il metodo delle condizioni minime e con il metodo del collegamento a due estremità.
Come si può vedere dalla Figura 4, i punti o e c sono i due punti bassi e i due punti finali della curva, mentre il punto d è il punto più alto.
Secondo il metodo delle condizioni minime, i punti o e c sono collegati dalla retta a1a1, come mostrato nella Figura 5. La retta a2a2 è tracciata parallelamente alla retta a1a1 attraverso il punto più alto d.
Il valore misurato lungo l'asse y nella regione racchiusa dalle due rette parallele a1a1 e a2a2, dopo l'elaborazione dei dati, rappresenta l'errore di rettilineità della guida δ ottenuto con il metodo delle condizioni minime.
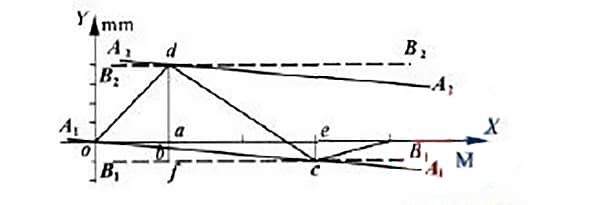
Secondo il metodo del collegamento a due punti, tracciare due rette parallele all'asse x passanti per i punti C e D rispettivamente.
Tali linee sono rappresentate dalle linee tratteggiate b1b1 e b2b2 nella Figura 5. Nella regione racchiusa da queste due linee parallele, il valore misurato lungo l'asse y, dopo l'elaborazione dei dati, rappresenta il valore dell'errore di rettilineità della guida tra i due punti finali.
Per determinare il metodo di deviazione minima e il valore di deviazione nei due punti finali, tracciare una retta parallela all'asse y che passi per il punto D, che intersechi l'asse nel punto A, che intersechi la retta a1a1 nel punto H e che intersechi la retta b1b1 nel punto F.
Allo stesso modo, tracciare una retta parallela all'asse y che passa per il punto C e interseca l'asse nel punto E.
(1) Determinazione dell'errore di rettilineità con il metodo delle condizioni minime
Secondo il metodo delle condizioni minime, il valore dell'errore di rettilineità δ della guida viene ricavato dal valore misurato lungo l'asse y dopo l'elaborazione dei dati, che rappresenta il metodo della deviazione minima.
Come mostrato nella Figura 5:
E poiché BD = BA + AD,
∆OAB e ∆OEC sono quindi due triangoli simili,
Riordinando l'equazione (3), si ottiene:
Sostituendo l'equazione (4) nell'equazione (2) e riordinando, si ottiene:
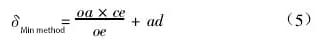
(2) Determinazione dell'errore di rettilineità con il metodo della connessione a due punti
Secondo il metodo del collegamento a due punti, il valore misurato lungo l'asse y dopo l'elaborazione dei dati rappresenta il valore dell'errore di rettilineità δ della guida tra i due punti finali.
Come mostrato nella Figura 5:
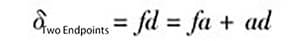
E poiché fa = ce,
(3) Calcolo dei valori di errore generati da due metodi di valutazione
L'equazione (6) meno l'equazione (5), vale a dire,
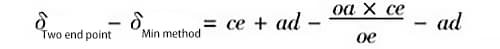
Riordinando, si ottiene:
(4) Calcolo dell'errore massimo generato da due metodi di valutazione
Nella Figura 5, sia ad = δ1, ce = δ2, oa = p; sia la lunghezza della guida da misurare l, allora oe = l - p e:
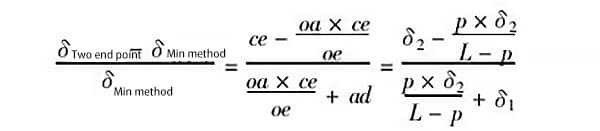
Ad esempio, se p = 0,5 m (cioè il passo è di 0,5 m), δ1 = 1,0δ, δ2 = 0,25δ e la lunghezza della guida misurata è l - 2 m, il rapporto dell'errore generato dai due metodi di valutazione è
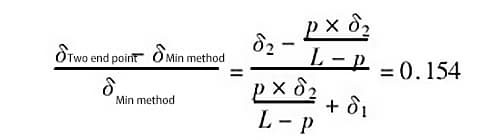
Il rapporto tra gli errori generati dai due metodi di valutazione è pari a 0,154, il che significa che l'errore generato dal metodo della connessione a due punti è maggiore di 15,4% rispetto a quello generato dal metodo della condizione minima.
Nell'equazione precedente, quando 
, cioè i punti più alti e più bassi della curva di errore sono infinitamente distanti, allora
, quindi otteniamo:
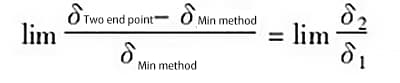
Ad esempio, quando δ1 = 1,0δ e δ2 = 0,25δ e la distanza tra i punti più alti e più bassi della curva di errore è infinitamente distante (cioè L=0,25), il rapporto tra gli errori generati dai due metodi di valutazione è 
, il che significa che l'errore generato dal metodo della connessione a due punti è 25% più grande di quello generato dal metodo delle condizioni minime.
Quando δ1 = δ2, cioè la distanza tra i punti più alti e più bassi della curva di errore è uguale, come mostrato nella Figura 6, i valori massimi di errore generati dai due metodi di valutazione sono:
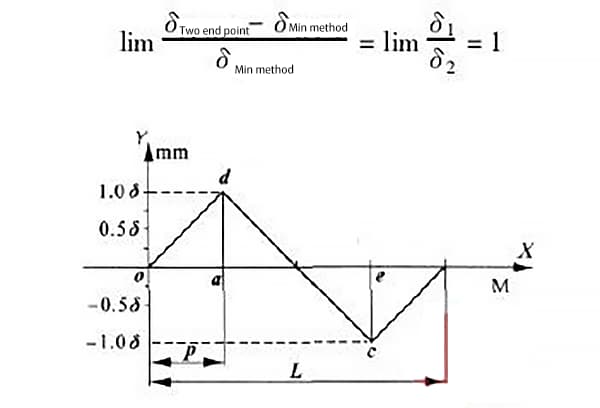
Da ciò si evince che quando i punti più alti e più bassi della rotaia di guida sono uguali e infinitamente distanti, l'errore massimo generato dai due metodi di valutazione è il più grande e può raggiungere 100%.
La tabella 1 elenca il rapporto degli errori generati dai due metodi di valutazione per diverse lunghezze della guida misurata, quando i punti della curva di errore sono distribuiti su entrambi i lati della linea di collegamento a due punti.
La distanza tra i punti più alti e più bassi della curva di errore è uguale quando il passo di misura p = 0,5.
Tabella 1 Rapporto di errore dei due metodi di valutazione
| Rapporto di errore | Distanza L (M) tra il punto più alto e quello più basso del binario di guida | ||||||
| 1 | 10 | 15 | 20 | 25 | 30 | 40 | ∞ |
 | 33.30% | 90% | 93.30% | 95% | 96% | 96.70% | 97.50% |
Se i punti della curva dell'errore di rettilineità si trovano sullo stesso lato della linea di connessione a due punti, allora gli errori generati dai due metodi di valutazione sono nulli, cioè i risultati ottenuti dai due metodi di valutazione sono uguali.
Se i punti della curva di errore di rettilineità si trovano su entrambi i lati della linea di connessione a due punti e i punti più alti e più bassi della curva di errore sono uguali e infinitamente distanti, allora l'errore massimo generato dai due metodi di valutazione è il più grande e l'errore generato dal metodo di connessione a due punti può essere 100% più alto di quello generato dal metodo di condizione minima.
Pertanto, quando si valuta l'errore di rettilineità delle guide delle macchine utensili di grandi dimensioni nella produzione pratica, è molto importante scegliere il metodo di valutazione appropriato. Quando i punti della curva di errore si trovano su entrambi i lati della linea di connessione a due punti, il metodo delle condizioni minime deve essere utilizzato come prima scelta per la valutazione.
In qualità di fondatore di MachineMFG, ho dedicato oltre un decennio della mia carriera al settore della lavorazione dei metalli. La mia vasta esperienza mi ha permesso di diventare un esperto nei campi della fabbricazione di lamiere, della lavorazione, dell'ingegneria meccanica e delle macchine utensili per metalli. Penso, leggo e scrivo costantemente su questi argomenti, cercando di essere sempre all'avanguardia nel mio campo. Lasciate che le mie conoscenze e la mia esperienza siano una risorsa per la vostra azienda.
IT 
EN 
AR 
DE 
ES 
FR 
JA 
NL 
PT 
PT_BR 
RU 
KO