Immaginate di trovarvi su un ponte e di veder passare un camion pesante. Vi siete mai chiesti perché il ponte non crolla sotto il peso? Questo articolo approfondisce i concetti di deformazione e stress, spiegando come i materiali si deformano sotto la forza e come gli ingegneri calcolano queste deformazioni per garantire la sicurezza. Imparerete le relazioni fondamentali tra queste forze, come si misurano e le loro implicazioni pratiche nelle strutture di tutti i giorni. Che siate ingegneri in erba o semplici curiosi, questa guida farà luce sulle forze invisibili che mantengono intatto il nostro mondo.

In primo luogo, la maggior parte del settore del monitoraggio della sicurezza consiste nel misurare la deformazione della struttura sottoposta a test. Una deformazione eccessiva può causare incidenti.
Ad esempio, le crepe nelle strutture, lo sprofondamento e lo spostamento tra la struttura e un riferimento fisso, sono grandi deformazioni visibili a occhio nudo e possono essere misurate in millimetri utilizzando misuratori come i misuratori di crepe, i livelli statici e i misuratori di spostamento.
Ma come si può rappresentare la piccola deformazione causata dalla compressione all'interno della struttura da testare o dalla flessione all'esterno dell'oggetto a forma di trave?
La risposta è la tensione.

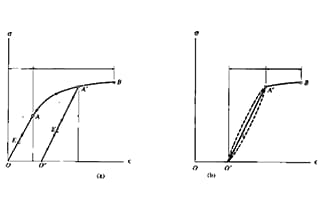
Supponiamo che la lunghezza di una struttura di lunghezza L subisca una deformazione sotto sforzo e che la sua lunghezza cambi in L', allora la sua variazione di lunghezza ΔL = L' - L, e la deformazione ε è il rapporto tra la variazione di lunghezza ΔL e la lunghezza originale L, la formula è la seguente:

Qual è l'unità di misura della deformazione?
Come si evince dalla formula, la deformazione è un rapporto ed è adimensionale, cioè non ha unità.
Che cos'è la microdeformazione?
Poiché il ΔL è molto piccolo, di solito nell'intervallo dei micron, il valore della deformazione calcolata è molto piccolo, con molti decimali, il che rende scomoda la visualizzazione e l'osservazione, per cui è stata introdotta la notazione scientifica 10-6, chiamata microdeformazione με, che può essere intesa come l'unità di misura della microdeformazione è 10-6, e il nostro campo di misura dell'estensimetro è ±1500 microdeformazioni, il cui valore positivo indica l'allungamento e quello negativo la compressione.
La deformazione è una piccola deformazione all'interno della struttura sottoposta a test, quindi perché si deforma? Perché è sottoposta a una forza esterna.
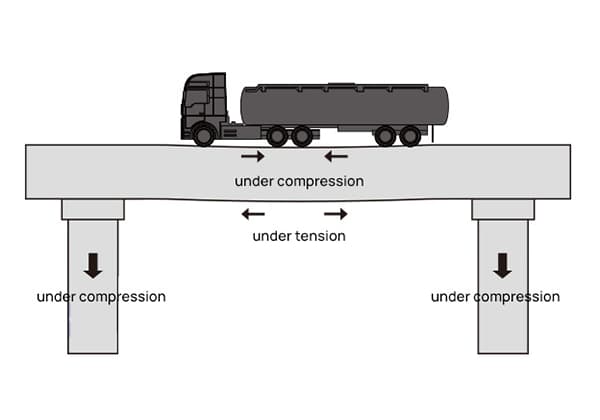
Prendendo come esempio il pilastro di un ponte, se un camion a pieno carico passa sul ponte, il pilastro sopporterà una pressione aggiuntiva e produrrà una compressione e una deformazione da compressione, mentre il pilastro produrrà una forza interna per contrastare la forza esterna e superare la deformazione.
Questa forza interna è lo stress. La sollecitazione è definita come la forza per unità di superficie, che è in realtà una pressione, con unità di MPa.
Qual è quindi la relazione tra la variabile della deformazione e la variazione della sollecitazione sopportata? Si veda la formula di calcolo:

Nella formula, σ rappresenta la sollecitazione, E è il modulo elastico del materiale in esame, noto anche come modulo di Young, che è una grandezza fisica che descrive l'elasticità del materiale.
Può essere vista come la capacità del materiale di resistere alla deformazione (rigidità) e, da una prospettiva micro, è la forza di legame tra atomi e molecole.
Due materiali con la stessa deformazione (lo stesso valore di deformazione), il materiale con una maggiore resistenza alla deformazione (un modulo elastico più grande) sopporterà una sollecitazione maggiore.
Ad esempio, se un tofu e un blocco di ferro della stessa dimensione vengono compressi in altezza di 1 mm, il primo deve essere premuto delicatamente a mano, mentre il secondo deve essere aiutato da uno strumento.
Il modulo elastico dei materiali ingegneristici più comuni è riportato in tabelle, ad esempio il modulo elastico del calcestruzzo C30 è di 30000MPa (1N/mm).2 = 1MPa), e il modulo elastico dell'acciaio al carbonio è 206GPa.
Il modulo elastico Ec del calcestruzzo a compressione e a trazione deve essere adottato secondo la Tabella 4.1.5.
Il modulo di deformazione a taglio Gc del calcestruzzo può essere adottato a 40% del corrispondente valore del modulo elastico.
Il rapporto di Poisson Vc del calcestruzzo può essere adottato pari a 0,2.
Tabella4.15 Modulo elastico del calcestruzzo (×104N/mm2).
| Grado di resistenza del calcestruzzo | C15 | C20 | C25 | C30 | C35 | C40 | C45 | C50 | C55 | C60 | C65 | C70 | C75 | C80 |
| Ec | 2.20 | 2.55 | 2.80 | 3.00 | 3.15 | 3.25 | 3.35 | 3.45 | 3.55 | 3.60 | 3.65 | 3.70 | 3.75 | 3.80 |
Nota:
1. Quando sono disponibili dati di prova affidabili, il modulo elastico può essere determinato sulla base dei dati misurati;
2. Quando al calcestruzzo viene aggiunta una grande quantità di additivi minerali, il modulo elastico può essere determinato in base ai dati effettivi misurati in base all'età specificata.
Tabella 1.1-13 Modulo elastico e rapporto di Poisson di materiali comunemente utilizzati
| Articolo | Modulo elastico E/GPa | Modulo di taglio G/GPa | Rapporto di Poisson μ | Articolo | Modulo elastico E/GPa | Modulo di taglio G/GPa | Teflon |
| Ghisa grigia | 118~126 | 44.3 | 0.3 | Zinco laminato | 82 | 31.4 | 0.27 |
| Ghisa sferoidale | 173 | 0.3 | Piombo | 16 | 6.8 | 0.42 | |
| Acciaio al carbonio, acciaio al nichel-cromo | 206 | 79.4 | 0.3 | Vetro | 55 | 1.96 | 0.25 |
| Acciaio legato | Vetro organico | 2.35-29.42 | |||||
| Acciaio fuso | 202 | 0.3 | Gomma | 0.0078 | 0.47 | ||
| Rame puro laminato | 108 | 39.2 | 0.31-0.34 | Bakelite | 1.96-2.94 | 0.69-2.06 | 0.35-0.38 |
| Rame puro trafilato a freddo | 127 | 48.0 | Sandwich di plastica fenolica | 3.92-8.83 | |||
| Bronzo fosforo-stagno laminato | 113 | 41.2 | 0.32-0.35 | Celluloide | 1.71-1.89 | 0.69-0.98 | 0.4 |
| Ottone trafilato a freddo | 89-97 | 34.3-36.3 | 0.32-0.42 | Nylon 1010 | 1.07 | ||
| Bronzo al manganese laminato | 108 | 39.2 | 0.35 | Cloruro di polivinile non plastificato | 3.14-3.92 | 0.35-0.38 | |
| Alluminio laminato | 68 | 25.5-26.5 | 0.32-0.36 | teflon | 1.14-1.42 | ||
| Filo di alluminio trafilato | 69 | Polietilene a bassa pressione | 0.54-0.75 | ||||
| Alluminio fuso bronzo | 103 | 41.1 | 0.3 | Polietilene ad alta pressione | 0.147-0.245 | ||
| Bronzo fuso in stagno | 103 | 0.3 | cemento armato | 13.73~39.2 | |||
| Lega di duralluminio | 70 | 26.5 | 0.3 | 4.9-15.69 | 0.1-0.18 |
Quando non è possibile misurare direttamente le sollecitazioni interne, queste possono essere calcolate misurando la deformazione e moltiplicandola per il modulo di elasticità del materiale.