In questo articolo esploriamo gli affascinanti concetti di resistenza e rigidità in ingegneria. Scoprirete come questi principi garantiscono la sicurezza e la durata degli oggetti di uso quotidiano, dai ponti agli schermi degli smartphone. Scoprite con noi i segreti delle meraviglie dell'ingegneria!

Per garantire le prestazioni ottimali e l'affidabilità di un sistema o di una struttura meccanica, ogni componente deve svolgere la funzione prevista in modo efficace ed efficiente. L'obiettivo primario della progettazione della sicurezza dei componenti ingegneristici è garantire che tutti gli elementi possiedano resistenza, rigidità e stabilità adeguate, assicurando così l'integrità complessiva e la longevità del sistema.
La stabilità è un concetto fondamentale in ingegneria, che si riferisce alla capacità di un componente di mantenere o ritrovare il suo stato di equilibrio originale quando viene sottoposto a forze esterne. Questo principio è fondamentale in vari scenari, come ad esempio:
Questi esempi illustrano l'importanza della stabilità per prevenire guasti catastrofici e garantire il funzionamento sicuro di sistemi e strutture meccaniche.
In questa discussione mi concentrerò sulla comprensione completa di due principi ingegneristici altrettanto cruciali: la rigidità e la resistenza. Questi concetti, insieme alla stabilità, formano la triade di considerazioni fondamentali nella progettazione della sicurezza dei componenti, e ciascuno di essi svolge un ruolo vitale nel determinare le prestazioni complessive, la durata e la sicurezza dei sistemi ingegnerizzati.
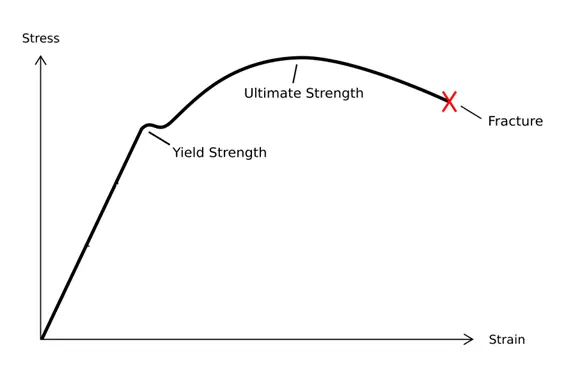
Definizione: La resistenza è la capacità di materiali, componenti o strutture di sopportare carichi o forze applicate senza cedimenti, deformazioni eccessive o danni. È una proprietà fondamentale nella scienza e nell'ingegneria dei materiali che determina la capacità di un materiale di resistere alle sollecitazioni meccaniche.
La forza comprende vari aspetti, tra cui:
Ad esempio, nella fabbricazione dei metalli, la comprensione della resistenza dei materiali è fondamentale per progettare componenti in grado di sopportare carichi operativi. Una trave in acciaio in un edificio deve avere una resistenza sufficiente a sostenere il peso della struttura e i carichi aggiuntivi senza piegarsi o rompersi.
La resistenza è influenzata da vari fattori, tra cui:
L'unità di misura della resistenza è tipicamente espressa in megapascal (MPa) o libbre per pollice quadrato (psi) in unità imperiali. Ad esempio, l'acciaio dolce ha una resistenza alla trazione di circa 400-550 MPa, mentre gli acciai legati ad alta resistenza possono superare i 1000 MPa.
Nel settore manifatturiero e ingegneristico, i calcoli e le prove di resistenza sono essenziali per la produzione:
Tecniche avanzate come l'analisi agli elementi finiti (FEA) e le prove distruttive sono spesso utilizzate per valutare e convalidare la resistenza di materiali e componenti in applicazioni ingegneristiche complesse.
Frattura fragile: Modalità di rottura improvvisa e catastrofica, caratterizzata da una rapida propagazione della cricca con una deformazione plastica minima. Questo tipo di cedimento si verifica senza preavviso e di solito si traduce in una superficie di frattura pulita e piatta.
Ad esempio:
Resa plastica: Una modalità di rottura in cui il materiale subisce una significativa deformazione plastica, con conseguente cambiamento permanente della forma e perdita dell'integrità strutturale. Questo tipo di rottura è generalmente più graduale e osservabile rispetto alla frattura fragile.
Ad esempio:
È importante notare che la modalità di rottura di un materiale dipende da vari fattori, tra cui le proprietà del materiale, le condizioni di carico, la temperatura e i fattori ambientali. Alcuni materiali possono presentare una transizione dal comportamento duttile a quello fragile in determinate condizioni, come le basse temperature o le elevate velocità di deformazione.
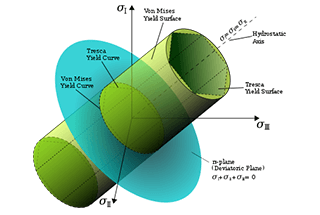
1. Teoria della massima tensione di trazione:
Quando la massima tensione di trazione σ1 in un punto dell'elemento raggiunge la tensione ultima σb in condizioni di sollecitazione unidirezionale, il materiale subisce una frattura fragile. Pertanto, i criteri per la rottura fragile di componenti con punti critici in condizioni di sollecitazione complessa sono: σ1 = σb.
Di conseguenza, le condizioni di resistenza stabilite dalla prima teoria della forza sono: σ1 ≤ σb.
2. Teoria della massima deformazione a trazione:
Quando la massima deformazione di trazione ε1 raggiunge il valore limite εu in condizioni di sollecitazione unidirezionale, il materiale cede per frattura fragile. Ciò può essere espresso come ε1 = εu.
Dalla legge di Hooke generalizzata, possiamo calcolare ε1 come: ε1 = [σ1 - u(σ2 + σ3)] / E, quindi σ1 - u(σ2 + σ3) = σb.
Le condizioni di resistenza stabilite dalla seconda teoria della resistenza sono: σ1 - u(σ2 + σ3) ≤ σb.
3. Teoria della massima sollecitazione di taglio:
Quando la massima sollecitazione di taglio τMax raggiunge la sollecitazione di taglio ultima τ0 in condizioni di sollecitazione unidirezionale, il materiale cede per snervamento. Ciò può essere espresso come τMax = τ0.
La formula per lo sforzo di taglio su una sezione inclinata durante la tensione assiale è τ0 = σs/2 (σs è lo sforzo normale sulla sezione). La formula per τMax è (σ1 - σ3)/2. Pertanto, la condizione di danno può essere riscritta come σ1 - σ3 = σs.
La condizione di resistenza stabilita dalla terza teoria della resistenza è: σ1 - σ3 ≤ σs.
4. Teoria dell'energia specifica del cambiamento di forma:
Quando il rapporto di variazione della forma in un punto dell'elemento raggiunge il valore limite in condizioni di sollecitazione unidirezionale, il materiale cede per snervamento.
La condizione di resistenza stabilita dalla quarta teoria della resistenza è:
√(σ1^2 + σ2^2 + σ3^2 - σ1σ2 - σ2σ3 - σ3σ1) < σs.

Definizione: La rigidità si riferisce alla capacità di un materiale, di un componente o di una struttura di resistere alla deformazione o allo spostamento elastico quando è sottoposto a una forza esterna. Quantifica la misura in cui un sistema può mantenere la sua forma e le sue dimensioni entro i limiti consentiti sotto i carichi applicati.
La rigidità è un parametro fondamentale in ingegneria che caratterizza il rapporto tra forza e deformazione in un materiale o in una struttura. È definita come il rapporto tra la forza applicata e lo spostamento risultante, che indica la quantità di forza necessaria per produrre un'unità di deformazione. In termini matematici, la rigidità (k) è espressa come:
k = F / δ
Dove:
L'unità di misura della rigidità è tipicamente la forza per unità di lunghezza, come N/m (Newton per metro) nel sistema SI o lbf/in (libbre-forza per pollice) nel sistema imperiale.
In termini pratici, la rigidità può essere concettualizzata utilizzando l'analogia di una molla. La costante elastica, che rappresenta la rigidità di una molla, è definita come il rapporto tra la forza di trazione o compressione applicata e l'allungamento o la compressione risultante. Questa relazione è descritta dalla legge di Hooke per i sistemi elastici lineari.
La comprensione e il controllo della rigidità sono fondamentali in diverse applicazioni ingegneristiche, tra cui:
Gli ingegneri devono bilanciare i requisiti di rigidità con altre considerazioni progettuali come la resistenza, il peso, il costo e la producibilità per creare soluzioni ottimali per applicazioni specifiche.
Quando il carico applicato è costante, si parla di rigidità statica.
Quando il carico si alterna, si parla di rigidità dinamica.
La rigidità statica comprende la rigidità strutturale e la rigidità di contatto.
La rigidità strutturale si riferisce alla rigidità dell'elemento stesso e comprende la rigidità flessionale e torsionale.
1. Rigidità a flessione: calcolata secondo la seguente formula:
K=P/δ
Dove
2. La rigidità torsionale è calcolata secondo la seguente formula:
Km=ML/θ
Dove M - coppia applicata (n - m);
L - distanza dalla posizione di azione della coppia all'estremità fissa (m);
θ-- Angolo di torsione (°)

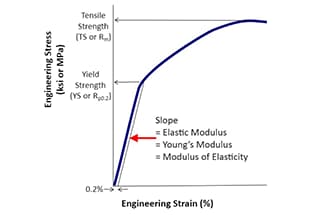
Dalla spiegazione della resistenza e della rigidità, si evince che la resistenza si concentra sul cedimento sotto l'azione di una forza esterna ed è classificata in cedimento per snervamento plastico e frattura fragile, in relazione alla curva sforzo-deformazione durante le prove di trazione. La rigidità, invece, si riferisce alla relazione tra deformazione e forza.
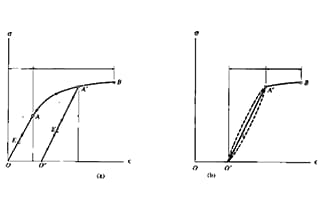
Come mostrato nella fig.
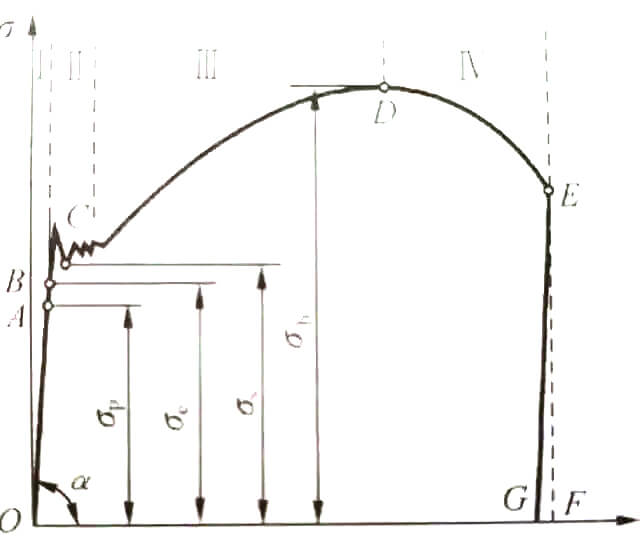
La curva in figura può essere suddivisa in quattro fasi:
1. Fase di deformazione elastica;
2. Stadio della resa;
3. Fase di rafforzamento;
4. Fase locale di scollatura.
La rigidità è definita come resistenza alla deformazione elastica, che si verifica nella fase iniziale, ed è regolata dalla legge di Hooke in condizioni elastiche.
Calcolo della rigidità flessionale e della rigidità torsionale in condizioni di carichi statici è simile alla legge di Hooke, suggerendo che la rigidità viene misurata solo durante la fase di deformazione elastica.
Nella fase successiva, quando si verifica la deformazione plastica durante la prova di trazione, la deformazione residua non scompare. Sulla curva sforzo-deformazione, sebbene la sollecitazione rimanga quasi invariata, la deformazione aumenta in modo significativo. A questo punto, la sollecitazione raggiunge il limite di snervamento e il materiale entra nella fase di rottura per snervamento plastico. Mentre la sollecitazione continua ad aumentare, anche la deformazione aumenta fino a raggiungere il limite di resistenza.
Pertanto, la misurazione della resistenza avviene dopo che il materiale subisce una deformazione elastica e prima che raggiunga il limite di resistenza.
In conclusione, sia la rigidità che la resistenza sono valutate durante la fase di rottura dei pezzi, con la rigidità misurata dalle sollecitazioni e la resistenza dalla deformazione.
In termini di ordine nel processo di deformazione, la rigidità si verifica nella fase iniziale, mentre la resistenza si verifica nella fase successiva.
Pertanto, nella valutazione delle condizioni di rottura dei pezzi, finché i requisiti di rigidità sono soddisfatti, il pezzo dovrebbe essere in grado di sopportare sollecitazioni sufficienti durante la fase di deformazione elastica, che a sua volta dovrebbe soddisfare i requisiti di resistenza.
Questa relazione si riflette in vari progetti, come l'albero delle apparecchiature meccaniche. In genere, la dimensione dell'albero viene determinata in base alle condizioni di resistenza e la sua rigidità viene verificata in base alle condizioni di rigidità.
Pertanto, i requisiti di rigidità per gli alberi dei macchinari di precisione sono molto elevati e la progettazione delle dimensioni della sezione trasversale è spesso controllata dalle condizioni di rigidità.