梁の曲げせん断応力と強度計算のエキスパートガイド

横力を受ける梁の断面には、曲げモーメントとせん断力の両方が作用し、その結果、断面には法線応力とせん断応力の両方が生じます。次に、いくつかの一般的な梁断面の曲げせん断応力について説明します。

長方形断面

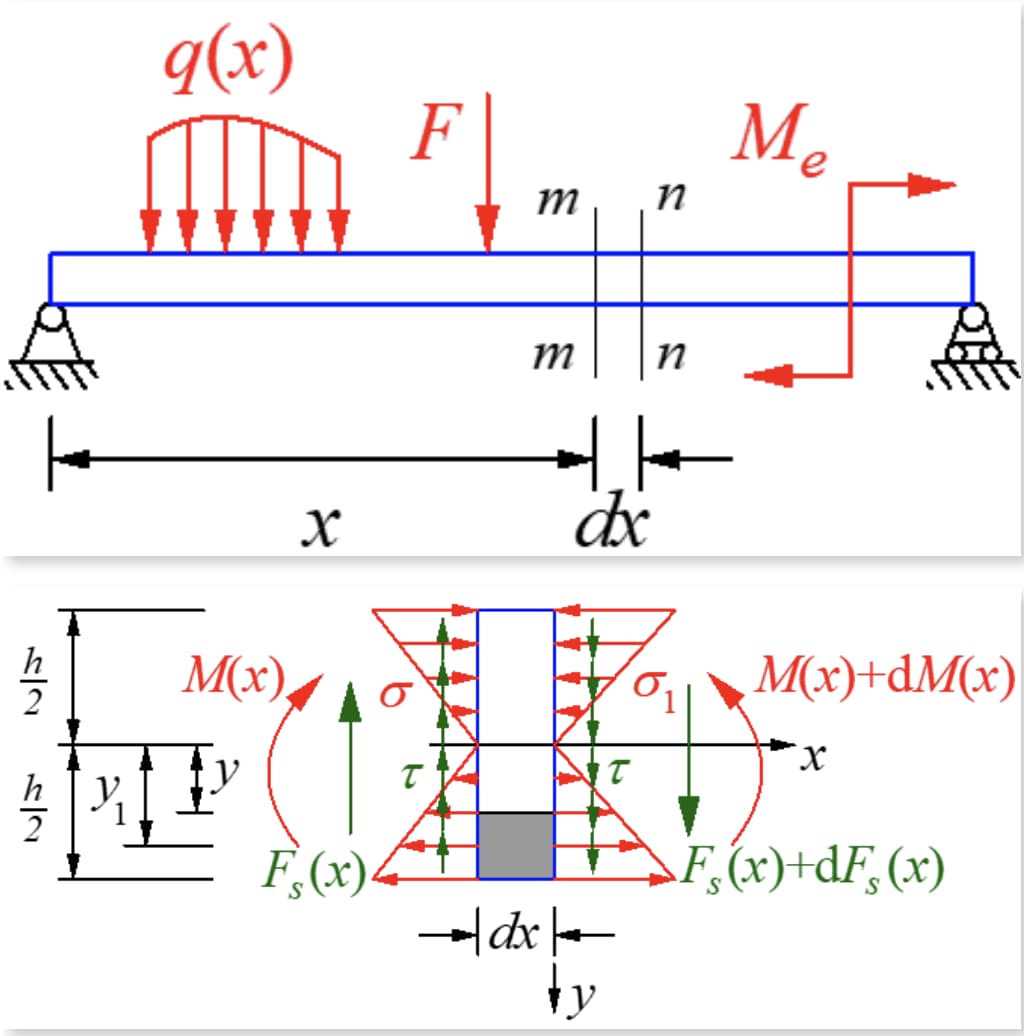
長さ dx の小さなセグメントを、横力曲げの状態で梁から切り取ります。梁には荷重がなく、セグメントの両側のせん断力は等しいが反対方向です。右側の断面の曲げモーメントは左側の断面の曲げモーメントより大きく、その結果、2つの断面の法線応力は異なります。

幅の狭い矩形断面では、梁の両側にせん断応力がないため、せん断応力は境界に接することになります。このことは、梁が対称的に曲げられて境界に平行であるため、対称軸のy軸上のせん断応力はy方向でなければならず、幅方向に沿ってほとんど変化しないことを意味します。

そこで、断面上のせん断応力の分布則について、以下の仮定を置く：

• 断面の各点におけるせん断応力の方向は、せん断力に平行である；
• すなわち、中立軸に平行な水平線上の各点におけるせん断応力は等しい。

断面の高さと幅の比が2より大きい場合、上記の仮定に基づく解は、弾性理論による厳密な解に比べて十分正確である。

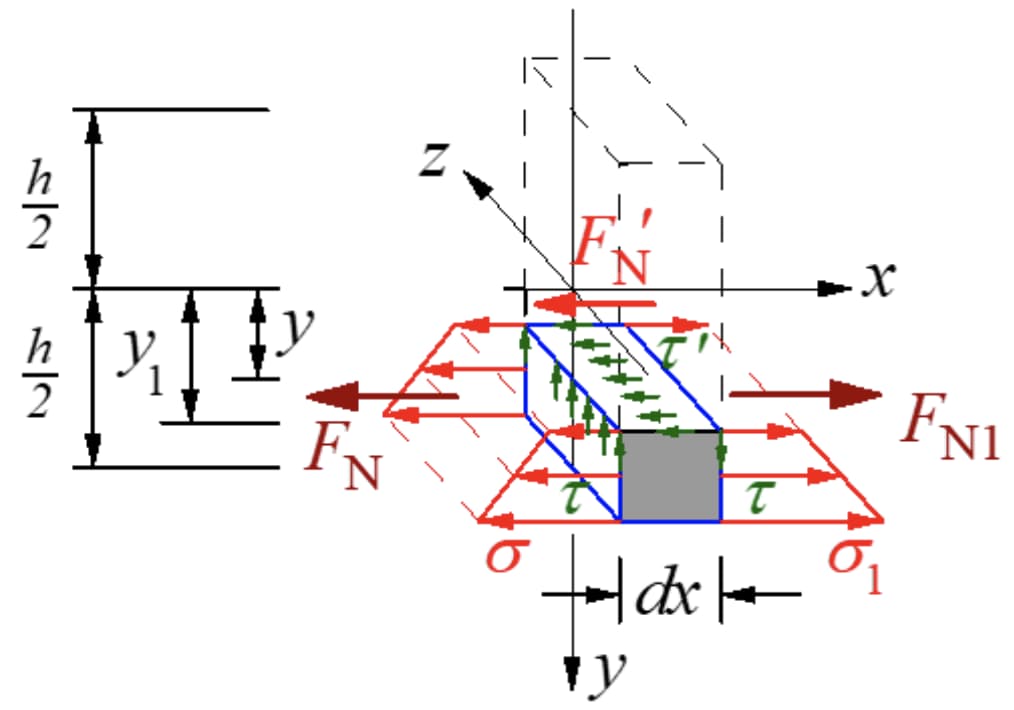
せん断応力の互恵定理によれば、断面に垂直な縦断面には断面の大きさに等しいせん断応力が存在するはずである。モーメント中立軸がyから離れるように縦断面に沿って微小セグメントを切り、縦断面の下側に微小要素を取る。力は下図のようになる。

その結果、左側のセクションにかかる法線応力は次のようになる：

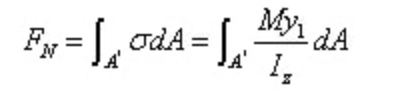
右側セクションにかかる法線応力の結果は次のようになる。

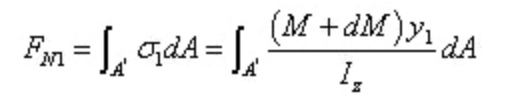
2つの結果の大きさが異なることは明らかである。マイクロセグメントのバランスを維持するためには、縦断面に軸方向に沿った力が存在しなければならない。この力はせん断応力の結果であり、縦断面にせん断応力が存在することが確認された。

dxは小さいので、縦断面のせん断応力を均等にする。

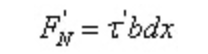
平衡条件によれば

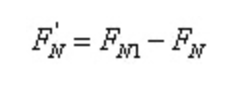
それはそうだ、

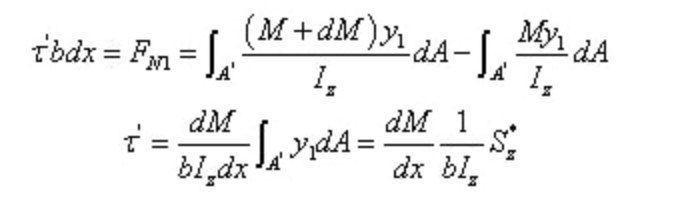
その中で

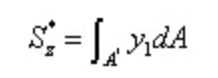
せん断応力の逆定理と、せん断力と曲げモーメントの微分関係から：

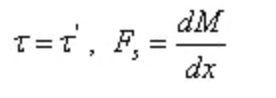
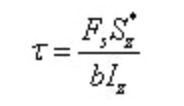
そのうちのひとつだ：

• bは断面上のモーメントyの中立軸と水平線の幅で、矩形断面では一定である；
• I_z は断面全体の中立軸の慣性モーメント；
• S_z* は、中立軸に対する断面上のyを中立軸とする水平線の外側の領域の静モーメントである；
• F_S は断面にかかるせん断力である。

その中で

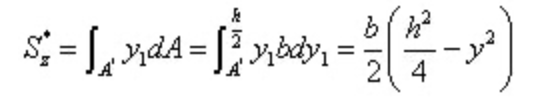
せん断応力の計算式に代入する。

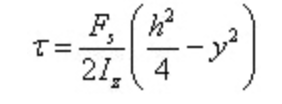
せん断応力は断面高さに沿って放物線状に分布する。

y=0のとき、中立軸の断面に最大せん断応力がかかる。

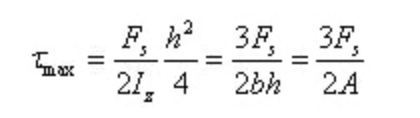
角ひずみは

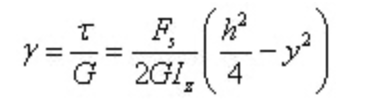
角ひずみも断面高さに沿って放物線状に分布していることがわかる。

このとき、クロスフォースが曲がったときの断面の反り形状は下図のようになり、クロスフォースの曲げ変形が平面仮定を満たしていないことが確認できる。

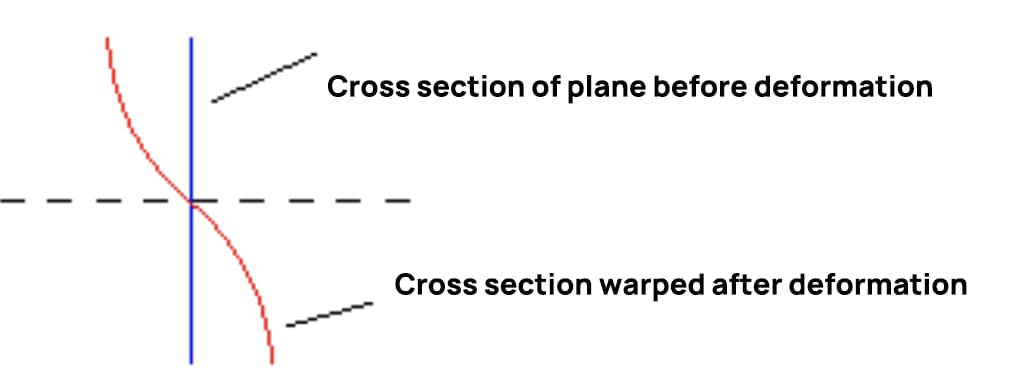
せん断力が一定の場合、連続する断面のせん断応力は等しくなり、反りの程度も等しくなる。縦繊維の長さは断面の反りによって変化しないので、法線応力が追加されることはない。断面の位置によってせん断力が変化すると、連続する2つの断面の反り度合いが異なり、断面に追加の法線応力が発生する。

他の形状の対称断面については、上記の方法で近似せん断応力解を導くことができる。

矩形断面の場合、応力計算式では断面幅(b)は一定であり、中立軸に対して片側の断面積の半分の静モーメントが最も大きくなる。その結果、中立軸上の各点におけるせん断応力が最大となる。

他の形状の対称断面では、断面の最大せん断応力は、中立軸上の様々な点に位置するのが一般的である。ただし、中立軸の幅が著しく大きい断面（十字断面など）や、幅が変化する断面（二等辺三角形断面など）は例外である。

したがって、I形、環状、円形断面の梁については、中立軸上の各点における最大せん断応力を主に後述する。

円形断面

円形断面の端の各点におけるせん断応力は、せん断応力の逆定理に従い、円周に接する。対称軸の各点では、せん断応力はy方向でなければならない。せん断応力の分布は、中立軸から幅yに沿った各点について対称軸上の点に収束すると仮定することができ、幅に沿った各点におけるY方向に沿ったせん断応力の成分は等しい。

円形断面の最大せん断応力はやはり中立軸上にあり、その方向は外力と平行で、中立軸上の各点で同じ値をとる。

最大せん断応力は

I字型断面

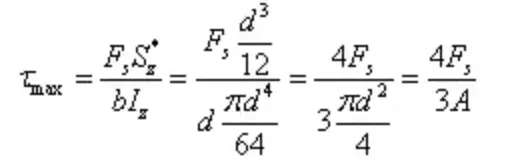
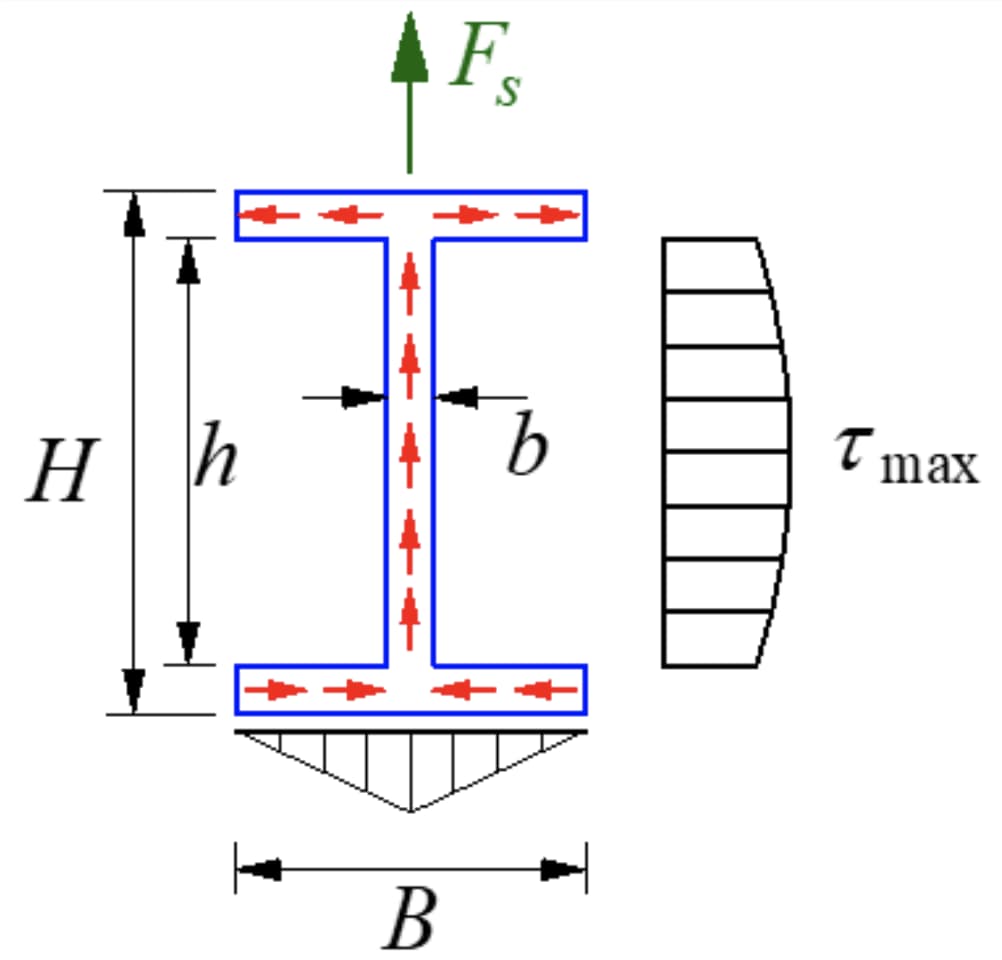
I型断面は、図のような応力分布を持つ薄肉開放断面である。肉厚に沿ったせん断応力の大きさは等しく、せん断応力流と呼ばれ、せん断方向に流れる。

フランジ上のy軸に平行なせん断応力成分は二次的なもので無視でき、フランジの長辺に平行な成分に主眼が置かれる。ウェブ上のせん断応力は放物線状の分布を持ち、その大きさは図に示されている。

最大せん断応力は中立軸にある。

の場合 I型鋼最大せん断応力：

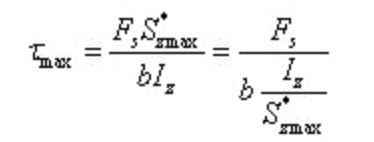
ここで、bはウェブの厚さであり、I_z/s*_{ゼットマックス} は、プロファイル・スチール・テーブルを参照して求めることができる。

細長い3つの長方形で構成されるI型断面であれば、ウェブの最大および最小せん断応力は以下のように求めることができる：

上記の2つの式から、ウェブの幅はフランジの幅よりはるかに小さいので、ウェブ上の最大せん断応力は最小せん断応力とあまり変わらないことがわかる。

したがって、ウェブ上のせん断応力はほぼ均等に分布していると考えることができる。

その結果、ウェブのせん断応力は全せん断力の95-97%を占め、断面のせん断力はほとんどウェブが負担する。

ウェブは断面にかかる剪断力のほとんどすべてを負担しており、ウェブにかかる剪断応力はほぼ均等に分布しているため、最大剪断応力は剪断力を腹極の断面積で割ることでおおよそ計算できる：

同時に Iビーム フランジは中立軸から最も離れており、各点の法線応力は比較的大きいので、フランジは断面の曲げモーメントのほとんどを負担する。

薄肉アニュラーセクション

薄肉の環状断面の厚さをd、環の平均半径をrとすると、厚さは平均半径よりはるかに小さいので、次のように仮定できる：

断面のせん断応力は肉厚に沿って等しくなる；

せん断応力の方向は断面の中心線に接し、せん断応力の流れ方向はせん断方向に沿っている。

最大せん断応力は中立軸上に位置する：

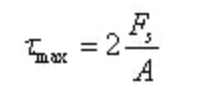
ここで、Aは環状部分の面積。

梁の強度状態

曲げ正規応力強度条件：

中立軸対称断面では、最大引張法線応力と最大圧縮法線応力は等しい。

一般的に使用されるプラスチック素材とその強度条件：

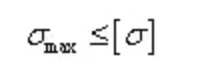
中立軸が非対称な断面については、最大引張法線応力と最大圧縮法線応力は等しくない。

脆い材料が一般的に使用され、その強度条件：

曲げせん断応力の強度条件は以下の通り：

梁の曲げ強度を向上させるための対策

曲げ法線応力は、梁を制御する主な要因である。

そのため、曲げ法線応力の強度条件が梁の設計の主な基礎となることが多い。

梁の耐力を向上させるためには、強度条件から2つの点を考慮する必要がある：

一方では、最大曲げモーメントを小さくするために、梁の応力を合理的に配置する必要があります；

一方、合理的な断面形状を採用することで、断面の曲げ断面係数を向上させ、材料の特性を最大限に活用している。

1.梁の応力を合理的に配置する。

梁の応力状態を改善し、梁の最大曲げモーメントを小さくする。

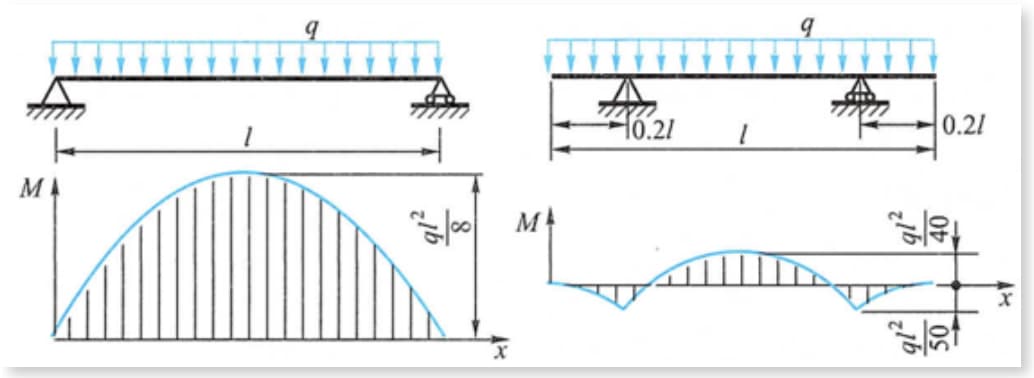
図に示すように、梁の両端位置から一定距離内側に支持部を移動させると、一様荷重時の梁の最大曲げモーメントが大幅に減少します。

例えば、ガントリークレーンの桁と円筒形コンテナは、支点が中央部にわずかに移動するため、最大曲げモーメントを減少させる効果が得られる。

2.妥当な梁の断面

曲げ断面係数が大きいほど、応力は小さくなり、梁の耐力は高くなる。

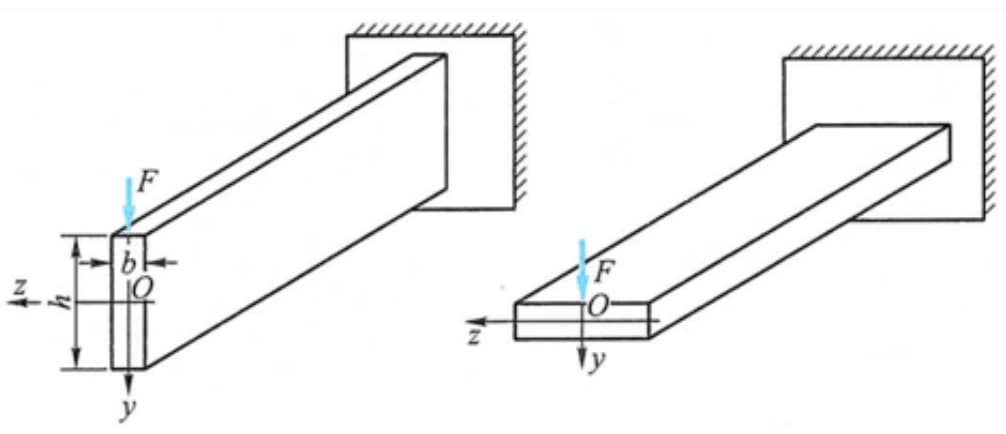
例えば、梁に鉛直方向の荷重がかかる場合、曲げ断面係数は垂直に配置した方が大きくなるので、水平よりも垂直に配置する方が合理的です。

断面の曲げ断面係数を改善すると同時に、より少ない材料で経済性を向上させたいと考えています。

そのため、一般に断面設計の合理性を測るには、断面積に対する曲げ断面係数の比が用いられる。

同じ断面積であれば、円形断面よりも長方形断面（高さが幅よりも大きい）の方が合理的であり、長方形断面よりもI字型断面や箱型断面の方が合理的である。

従って、素材を十分に生かすためには、素材は中立軸からできるだけ離して配置する必要がある。

セクションの合理的な形状を議論する際には 機械的性質 を考慮する必要がある。

同じ引張強度と圧縮強度を持つ材料（低炭素鋼など）は、円形、長方形、I字形、箱形などの中立軸対称断面を採用すべきである。

こうすることで、断面の上端と下端における最大引張応力と最大圧縮応力を等しくすることができる。

引張強さと圧縮強さが不均等な材料（鋳鉄、セメントなど）については、中立軸を引張側に傾けた断面形状を採用する。

等強度梁の概念

上述した梁はすべて等断面であり、曲げ断面係数は一定ですが、一般に梁の各断面の曲げモーメントは断面の位置によって変化します。

等しい直線梁の断面設計は、最大曲げモーメントに従って行われるべきであり、その最大応力は許容応力に近い。

他のセクションの曲げモーメントは小さいので、応力は小さく、材料は十分に利用されていない。

材料を節約し、自重を減らすために、曲げモーメントに応じて曲げ断面係数が変化するように断面サイズを変えることができる。

曲げモーメントが大きいところには大きな断面が使われ、曲げモーメントが小さいところには小さな断面が使われる。

このように軸に沿って断面が変化する梁を可変断面梁と呼ぶ。

可変断面梁の各断面にかかる最大法線応力が等しく、許容応力に等しい場合、その梁は等強度梁と呼ばれます。