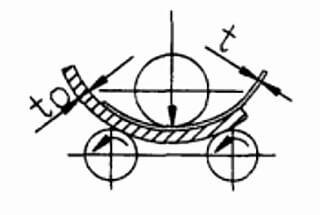
機械のローラー間の中心距離を計算するのに苦労したことはありませんか?このブログでは、この重要な測定値を求める簡単な方法をご紹介します。当社の専門メカニカルエンジニアが、貴重な洞察と実践的な例を示しながら、そのプロセスをご案内します。最後には、この一般的な課題に取り組む方法を明確に理解し、機械設計のスキルを向上させることができるでしょう。
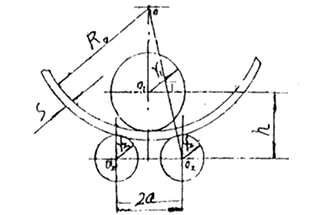
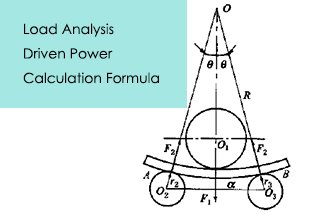
ボイラーや圧力容器の製造において、成形技術は主要な製造工程のひとつである。
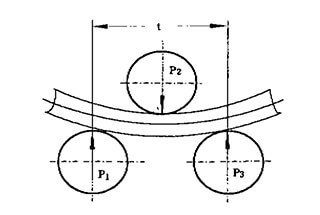
成形工程では、円柱部分の圧延が最も基本的な成形方法である。圧延には多くの作業が伴う。成形工程のほとんどは、左右対称の3本ロール曲げ機で行われる。しかし、シリンダー部の肉厚や直径は生産工程の条件によって決まるため、仕様や品種はかなり多い。
成形後の曲率の精度は、圧延終了時の上下ローラー間の中心距離であるパラメータ「H」に依存する。
このパラメーターは通常、式(1)によって決定される。
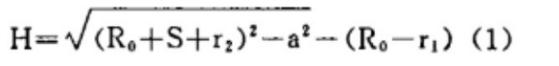
この計算式は複雑ではないように思えるかもしれないが、メーカーにとっては、シリンダー部分の仕様や種類が多岐にわたるため、累積作業量は相当なものになる。
異なる条件下での "H "の値の決定を単純化し、容易にするために、本稿では以下の2つの図式的アルゴリズムを使用する。
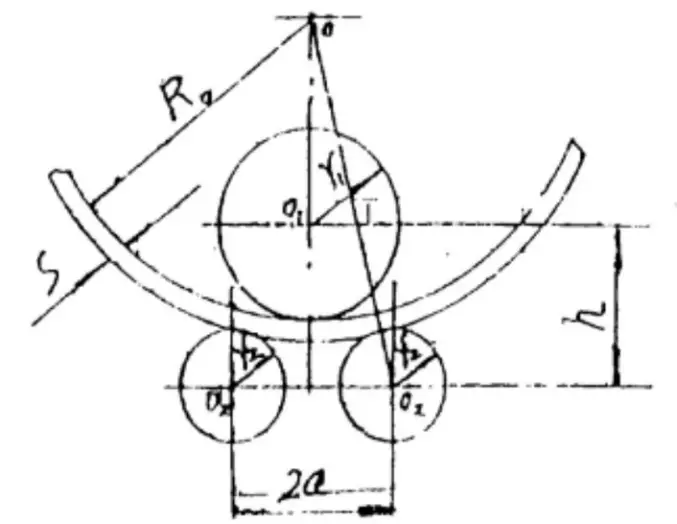
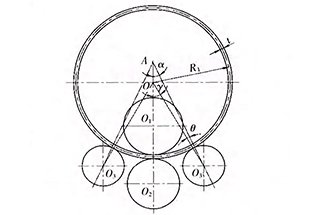
図1 左右対称3本ローラーの端部位置図 板曲げ機
ある種の 板圧延機 が与えられると、パラメータ a, r1 および2 は定数で、s とR0 は変数である。
したがって、ある種の 板曲げ機 は、任意の厚さと曲率半径を圧延するために使用され、対応する主パラメータ "h "は、以下のグラフアルゴリズムによって求めることができる。
まず、aを縦軸、hを横軸とする長方形座標系を確立する。
そして、座標系(図2)で次のような描画を行う。
OP=aを縦軸で横切り、点Pを円の中心とし、(R0 + S + r2)を半径とし、円弧の交点の横軸上に正の点aを作る。
点aを円の中心とし、R0 を半径とし、逆を円弧の横軸上の点Bとする。
そして、点Bを円の中心とし、R1 を円弧の交点の半径とし、円弧の横軸の正方向に点Cを作る。
したがってOC = h.
例えば、こうだ、
S = 20 mm、d = 2 000 mmのドラムセクションは、70 × 4000対称3ロール板曲げ機で圧延される。
hの値を計算する。
データによると、R1 = 350mm、R2 = 330mm、2a = 800mm。
グラフ・アルゴリズム(図2)によると、h=640mm:
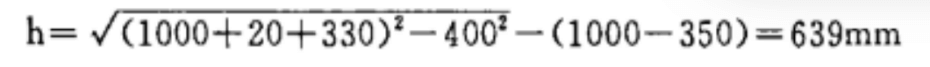
絶対誤差はわずか1mmで、真値の0.015%を占める。
R+S+r)を移動定規にすると便利。
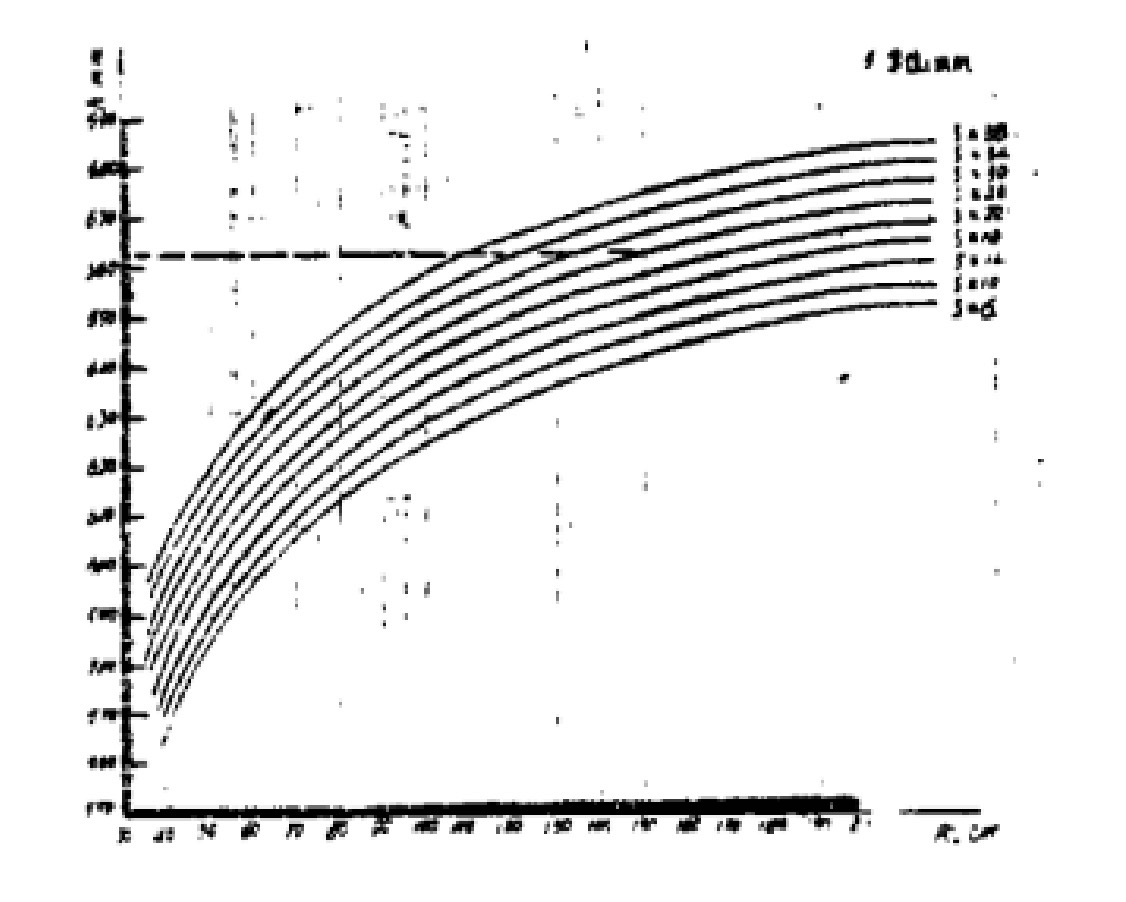
図2 "h "を計算するためのノルモグラム
上記のように、ある特定の 曲げ マシンのパラメータa, R1 とR2 は固定されている。
とすると、R0 異なる板厚でのhをrに描く。0-h座標系、Rの共通点グラフ0 このタイプでは、板厚の異なる鋼板のhとhが異なる。 圧延機 が得られる。
この種の板曲げ機では、あらゆる異なる条件下でドラム部の主要パラメータ「h」の値を求めることができ、非常に便利である。
以下は、70×4000の対称3面体の共通点図である。 ローラープレート ベンディングマシン。
既知:R1 = 350mm、r2 = 330mm、a = 400mm
だから
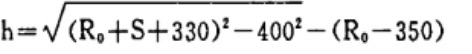
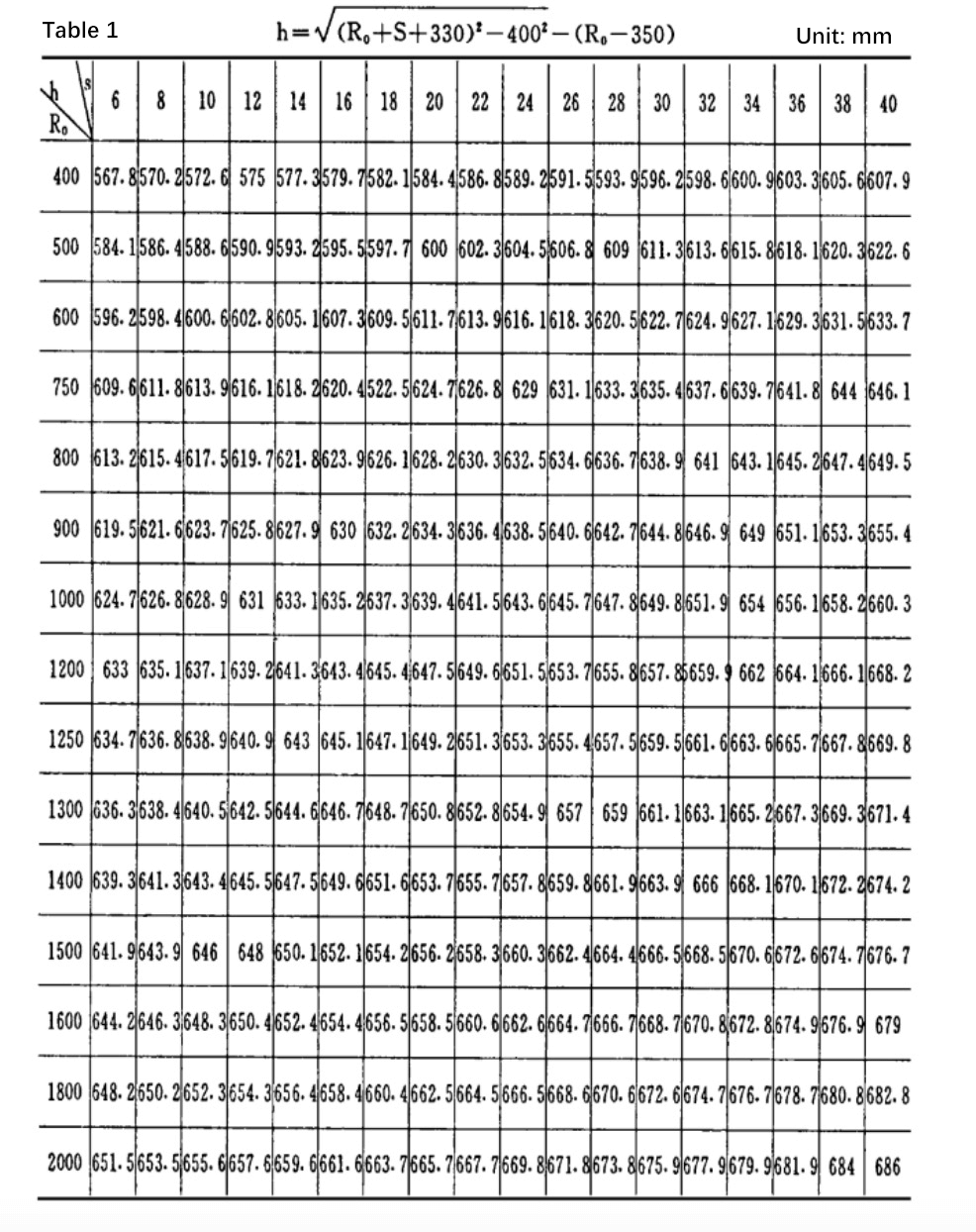
表1はs間隔2mmでの計算と図面のデータ表である。
実際の経験によると、厚さは 圧延機 は一般的に6≦s≦40(mm)である。
一般に、圧延ドラムの半径は400≦Rである。0 ≤ 200 (mm)。
したがって、この範囲を計算の描画範囲として使用する。
表1からわかるように、ある種の板曲げ機を用いて一定量のRを圧延する場合、nの値は基本的に板厚sに相当する。0.
実測値との誤差は0.05%以下。
しかし、銅板を曲げると、塑性変形と弾性変形の両方が生じる。
そのため、除荷後は一定の弾性回復がある。
従って、実際の生産では、実際の値よりも若干低い値になるはずである。
このように、両者の等価変化の法則を用いれば、図面が簡略化され、弾性体であることがわかる。 スプリングバック 実際の曲げを補正することができる。
同時に、グラフの線を小さくすることができ、任意のSに対応する "h "値を、あるR0.
前者のグラフ・アルゴリズムは普遍的なものであるが、後者はある種の板曲げ機に対するものであり、その板曲げ機は特殊な(k-R0-S)コポイント・グラフ。
教育における2つのグラフ・アルゴリズムの結果は非常に良く、生徒を大いに啓発している。
特に後者の方法には一定の実用性がある。
板曲げ機の製造業者は、(n-R0-S)である。 圧延機 これは、メーカーの実際の生産に大きな利便性をもたらす。