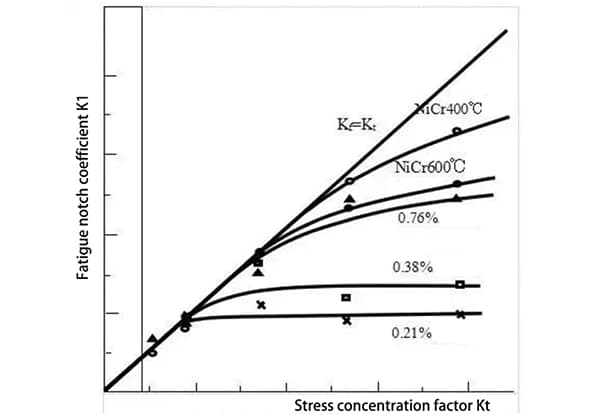
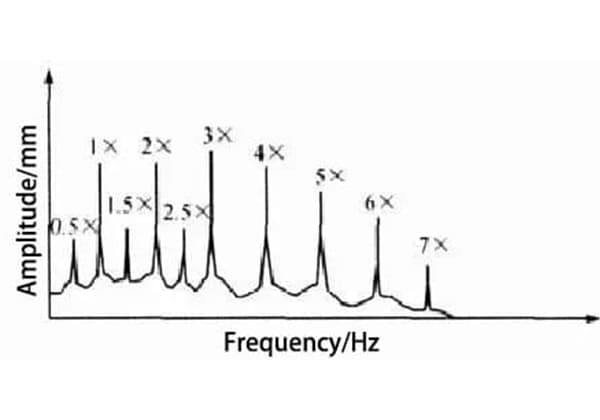
エンジニアは、材料が繰り返し応力下でいつ破壊するかをどのように予測しているのでしょうか?この記事では、疲労解析の重要なツールであるS-N曲線を紹介します。材料の疲労寿命を予測するために、平均応力、多軸応力変換、不規則応力がどのように扱われるかを学びます。これらの概念を理解することは、より耐久性と信頼性の高いコンポーネントの設計に役立ちます。疲労解析の複雑さを理解し、エンジニアリングプロジェクトを長持ちさせましょう。
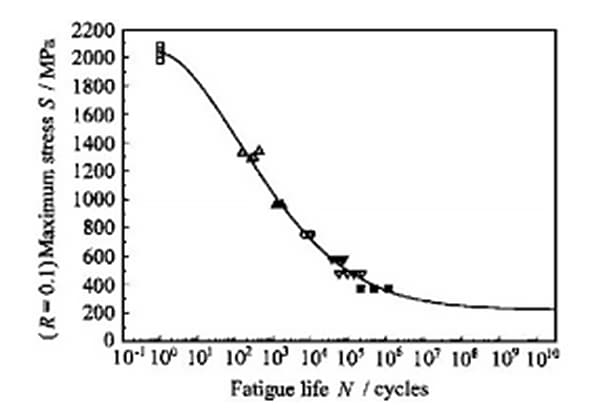
材料の疲労特性は通常、S-N曲線として知られる一軸応力サイクルによって表されます。この文脈では、破壊力学に基づく疲労理論は考慮されていないことに注意することが重要です。
応力の経時変化は、正弦波、方形波、パルスなどの規則的なパターンに従うことが多い。しかし、疲労性能に対する平均応力の影響は軽視されがちです(すなわち、r=S分/Sマックス ≠ -1).
現実には、応力状態は通常多軸で、応力変動は不規則であり、r≠-1である。実際の応力と実験室で測定された疲労性能の対応関係は、規則的な応力変動、一軸応力、r=1を含み、疲労解析の基礎を形成します。
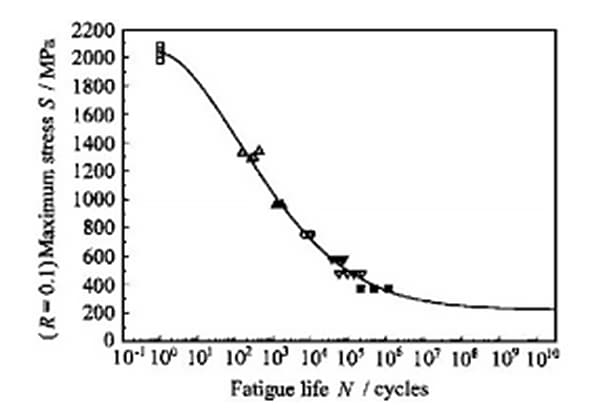
異なるr値に対するS-N曲線が存在する場合、未知のr値に対するS-N曲線を決定するために、一般的に補間法が採用される。
r=-1のS-N曲線しかない場合は、以下の式を用いて等価応力を計算することができます。この式は、r≠-1の一軸応力をr=-1のときの一軸応力に変換するもので、これを等価応力といいます:
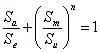
ここで、Sa は半応力振幅、Se は望ましい等価応力、Sm は平均応力であり、Su とnは異なる理論を構成する:
変換に使用する応力のタイプを決定するために、以下の応力オプションが利用可能です:フォンミーゼス等価応力、最大せん断応力、最大主応力、または特定の応力成分(Sx、Syz など)。
時には、大きさを変えずに符号を付けたミーゼス応力も採用されます。符号は最大主応力の符号に対応します。この方法の利点のひとつは、平均応力やrに反映される引張や圧縮の効果を考慮できることです。
に似ている。 強度理論フォンミーゼス等価応力と最大せん断応力換算は延性の高い材料に適しており、最大主応力換算は脆性材料に適している。
不規則な高低の等価一軸応力時間曲線を解析し、一連の単純応力サイクル(Sa, Sm)と対応する時間。
計数や統計は、パス依存法やパス非依存法など、さまざまな方法を用いて行うことができる。
経路相関法は最も広く使われている雨流計数法であり、計数プロセスを完了するために適用される。そのアルゴリズムと原理は「Downing, S., Society, D. (1982) Simplified rain flow counting algorithms.Int J Fatigue, 4, 31 - 40 "に記載されている。
雨水処理後、不規則な応力時間曲線は一連の単純なサイクル(Sa, Smそしてiniはサイクル数)。
この方法では、損傷蓄積理論(マイナー基準)を適用して計算・分析することができる:和(ni/Niここで、Ni は応力サイクルに対応する寿命である(Sa, Sm上記参照)。
この手法は、あるサイクル数後の安全係数や、特定の複雑な応力サイクルに対応する寿命を測定するために一般的に使用される。
現在、市販されている疲労解析ソフトウェアのほとんどは、前述のプロセスに基づいている。
しかし、疲労解析は経験的な解析であり、成熟した完全な理論は現在のところ存在しないことに留意すべきである。
多軸応力から一軸応力への変換に関しては、様々な見解がある。
例えば、フォンミーゼス応力は、形状変化の比エネルギーの考え方に基づく応力寸法量である。
プラスとマイナス、あるいは張力と圧縮という概念を使うのは不正確な方法であり、推奨されない。
採用する応力タイプの選択は、材料や構造物に発生する可能性のある亀裂の傾向によって決まり、どの種類の応力が主要な制御要因であるかを決定します。 疲労故障.
工学的実践によれば、良好な塑性を持つ鋼材は、以下のような場合、主応力の動的負荷の繰り返しによって損傷することが多い。 疲労故障.
平均ストレス効果の治療に関する補足:
"異なるR値でのS-N曲線が存在する場合、一般的には未知のR値でのS-N曲線を決定するために補間法が使用される。"
これは1つの方法であり、チェックする応力が複数ある場合に有効である。しかし、応力寿命が1つしかない場合には、この方法は面倒である。
もう一つの方法は、R=-1の条件下で等価応力半値振幅を決定し、S-N曲線を直接適用する方法である。
平均応力がある場合、S-N曲線を直接使用することはできません。代わりにGOODMAN CURVEまたは修正GOODMAN CURVEを使用します。