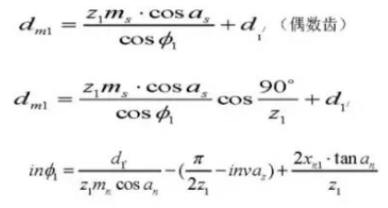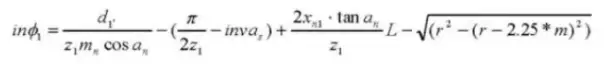ギア素材の選択：考慮すべき重要な要素
適切なギア材質を選択することは、なぜエンジニアリングにおいて非常に重要なのでしょうか？適切な材料を選択することで、歯車は耐摩耗性、耐久性、効率などの要求を満たすことができます。この記事では、様々な歯車材料について説明します。
歯車の魅力的な世界を不思議に思ったことはありませんか？このブログでは、この重要な機械部品の歴史、種類、用語についてご紹介します。ベテランの機械エンジニアの専門的な知識をもとに、歯車の複雑な世界を掘り下げていきます。歯車が何世紀にもわたってどのように進化してきたかを知り、現代の機械における重要な役割について学びましょう。
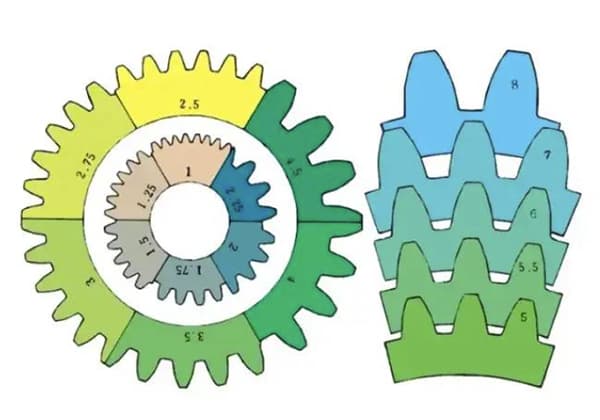
歯車は、他の歯車や歯付き部品と噛み合うように設計された、精密工学的に設計された歯付き機械部品である。動力伝達システムの基本要素であり、回転速度とトルクをシャフト間で変換する。歯車は円形で、外周に沿って等間隔に歯が配置されているのが特徴です。
ギアは、機械的なトランスミッションや、より広い機械工学の分野全体において、非常に多様かつ重要な役割を担っています。単純な手動工具から複雑な産業機器や高性能車両に至るまで、歯車は様々な機械や装置に不可欠です。歯車は、機械システムにおける速度、方向、力の精密な制御を可能にし、パワートレイン、減速機、ディファレンシャル、その他数え切れないほどの機械アセンブリに不可欠なものとなっています。
歯車の多様性は、平歯車、はすば歯車、かさ歯車、ウォーム歯車など、様々なサイズ、材質、構成で製造できることに起因しており、それぞれが特定の用途や性能要件に適しています。技術の進歩に伴い、歯車の設計と製造は進化を続けており、新しい材料、製造技術、最適化手法を取り入れ、機械システムの効率、耐久性、騒音低減を高めています。
紀元前350年には、ギリシャの有名な哲学者アリストテレスがその文献の中で歯車について記録している。
紀元前250年頃、数学者のアルキメデスも、タービンとウォームギヤを巻き上げ機に使用することを文献に記している。
イラクのクテシビオス水時計には、キリストより何世紀も前の歯車が今も保存されている。
中国における歯車の歴史は古代にさかのぼり、その歴史は長く広範囲にわたる。史料によると、古代中国では紀元前400年から200年前にはすでに歯車が使用されていたという。
山西省で発掘された青銅製の歯車は、これまでに発見された世界最古の歯車である。古代の科学技術の成果を反映した誘導車は、歯車機構を中心に回転する機械装置だった。
15世紀後半のイタリア・ルネサンス期、万能の天才として名高いレオナルド・ダ・ヴィンチは、文化的・芸術的側面に忘れがたい足跡を残しただけでなく、歯車技術の歴史にも多大な貢献をした。
500年以上経った今でも、現在の歯車には当時の試作品のスケッチが残されている。
(1) 平歯車
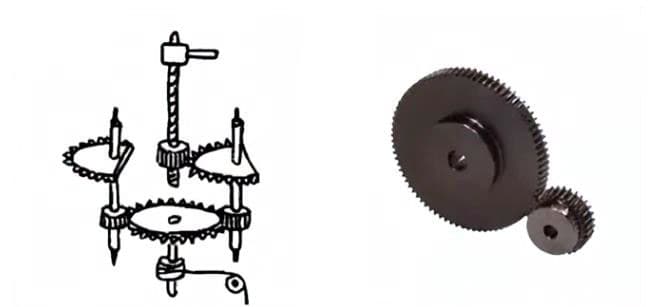
(2) ラック＆ピニオン
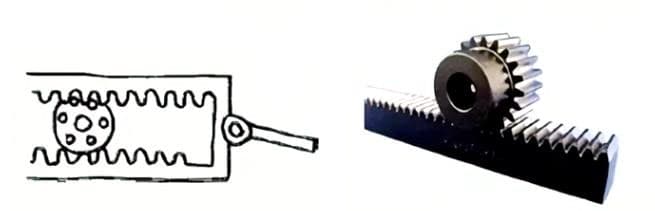
(3) 交差軸付きヘリカルギア
(4) かさ歯車
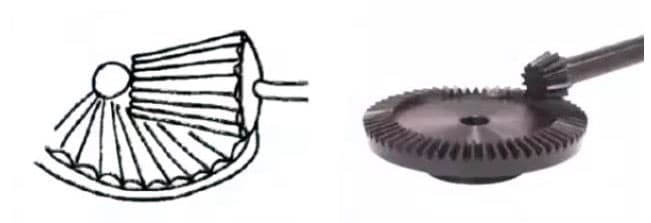
(5) 高変速比ハイポイドベベルギア
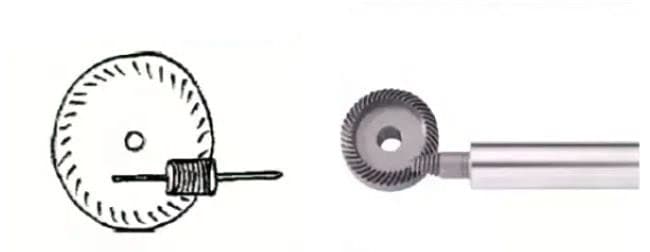
(6) ウォームギア
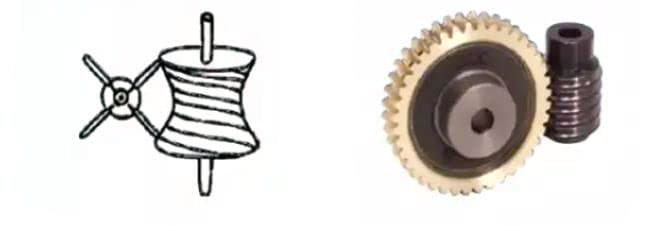
車輪の歯形が正確に運動を伝達することができると研究されるようになったのは、17世紀後半になってからである。18世紀にヨーロッパで産業革命が起こると、歯車伝動はますます広く応用されるようになった。
最初にサイクロイド歯車が開発され、次にインボリュート歯車が開発された。20世紀初頭には、インボリュート歯車が主流となりました。その後、ヘリカルギア、アークギア、ベベルギア、スキューギアなどが開発されました。
今日、現代の歯車技術は大きな進歩を遂げている。歯車モジュールは0.004ミリから100ミリまで、歯車の直径は1ミリから150メートルまであります。また 送電 能力は最大10万キロワットに達し、回転速度は毎分10万回転にも達する。最高周速は毎秒300メートルに達する。
国際的に動力伝達用歯車装置は、小型化、高速化、標準化に向けて発展している。歯車設計の動向としては、特殊歯車の適用、遊星歯車装置の開発、低振動・低騒音歯車システムの研究開発などがあります。
歯車には様々な種類があり、最も一般的な分類方法は歯車の軸に基づくものである。
一般に歯車は、平行軸、交差軸、スキュー軸の3種類に分類される。
平行軸ギア： スパーギア、ヘリカルギア、インターナルギア、ラック、ヘリカルラックを含む。
I交差軸ギア： ストレートベベルギア、スパイラルベベルギア、0度ベベルギアなど。
スキュー軸ギア： 軸が交差したヘリカルギア、ウォームギア、ハイポイドベベルギアなどを含む。
| ギア・トランスミッションのタイプ | ギアの種類 | 伝送効率（%） | 3Dグラフィカル表現 |
平行軸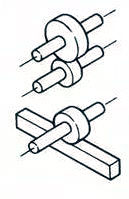 | スパーギア | 98.0-99.5 |  |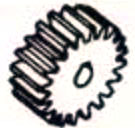
| ヘリカルギア |  | ||
| ラック、ヘリカルラック |  | ||
| インテンショナルギア |  | ||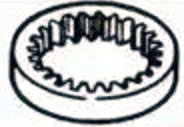
交差軸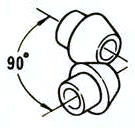 | マイターギア | 98.0-99.0 |  |
| ストレートベベルギア |  | ||
| スパイラルベベルギア |  | ||
スキュー軸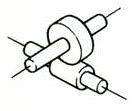 | スクリューギア | 70.0-95.0 |  |
| ミミズ | 30.0-90.0 |  | |
| ウォームホイール |  |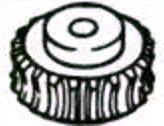
上表の効率は伝達効率であり、軸受や撹拌潤滑による損失は含まれていない。平行軸と交差軸の歯車対のかみ合いは基本的に転がりで、相対すべりが非常に小さいので効率が高い。
ヘリカルギヤやウォームギヤなどの千鳥軸歯車対は、相対的な摺動によって動力伝達を行うため、摩擦の影響が大きく、他の歯車に比べて伝達効率が低下する。
歯車の効率とは、通常の組み立て状態における歯車の伝達効率を指す。
不適切な取り付け、特にベベルギヤの組立距離が不正確で、同じベベルの交差点で誤差が生じる場合、その効率は著しく低下する。
1. スパーギア
歯筋と軸線が平行な円筒歯車。加工が容易なため、動力伝達用として広く用いられている。
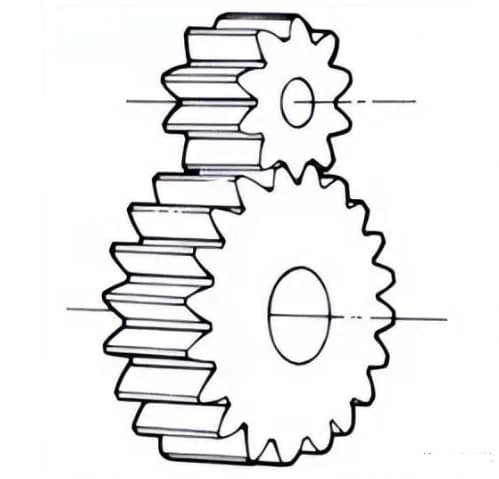
2.ラック
平歯車と噛み合う直歯の歯車。平歯車のピッチ径が無限に大きくなる特殊なケースと見ることができる。
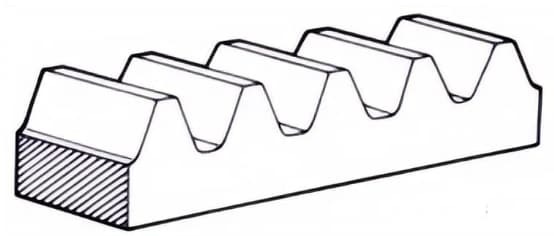
3.インターナルギア
平歯車と噛み合うリングの内側に歯を加工した歯車。主に遊星歯車の伝動機構やギヤカップリングなどに使用される。
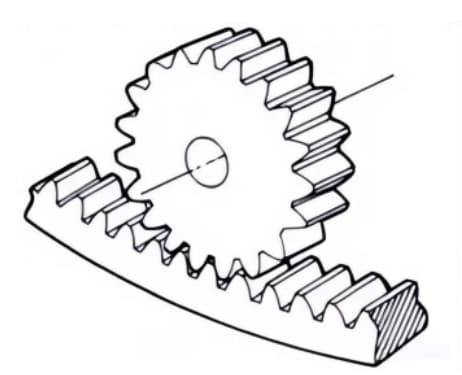
4.ヘリカルギア
歯が螺旋状に並んだ円筒歯車。平歯車に比べて強度が高く、滑らかに動くので広く使われている。伝達時に軸方向のスラストを発生させる。
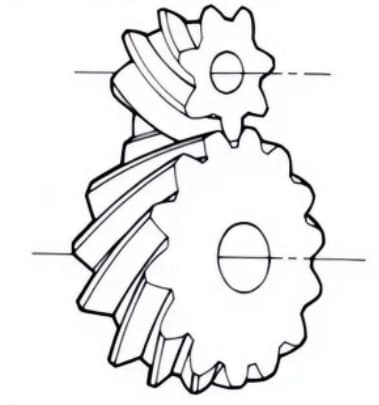
5.ヘリカルラック
ヘリカルギアと噛み合うラックギアのこと。ヘリカルギアのピッチ径が無限に大きくなる場合に相当する。
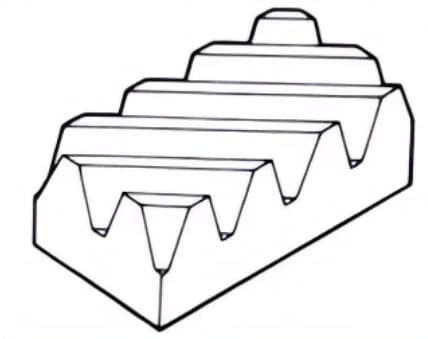
6.ヘリングボーン・ギア
はす角が反対の2つのはすば歯車からなる歯車。軸方向のスラストが発生しないという利点がある。
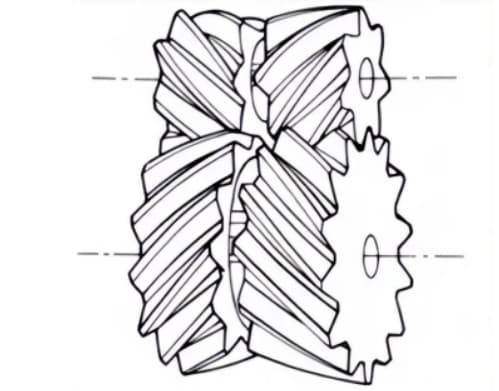
1.ストレートベベルギア
歯すじが円錐の母線に平行なかさ歯車。他の傘歯車に比べて製造が比較的容易である。
そのため、動力伝達用のかさ歯車用途に広く使用されている。
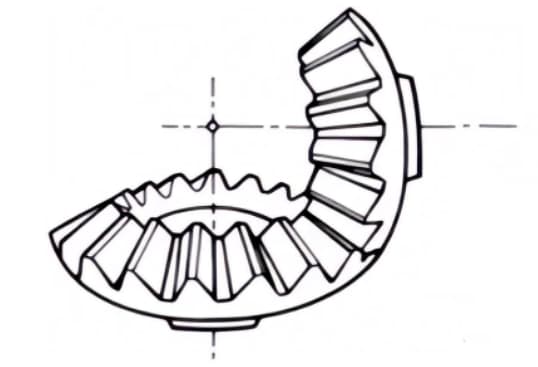
2.スパイラルベベルギア
歯筋が湾曲し、ねじれ角のあるかさ歯車。ストレートベベルギアよりも製造が難しいが、高強度・低騒音のギアとして広く使われている。
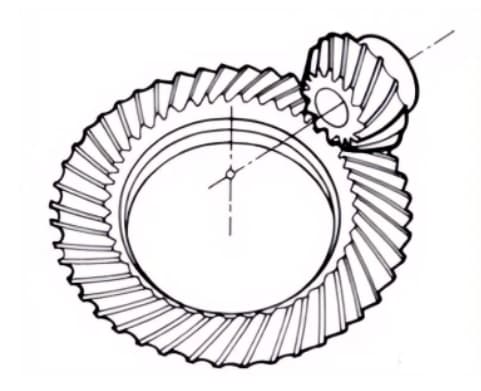
3.ゼロベベルギア
ねじれ角が0度のカーブベベルギア。ストレートベベルギアとスパイラルベベルギアの両方の特徴を持ち、歯面にはストレートベベルギアと同じ力がかかる。
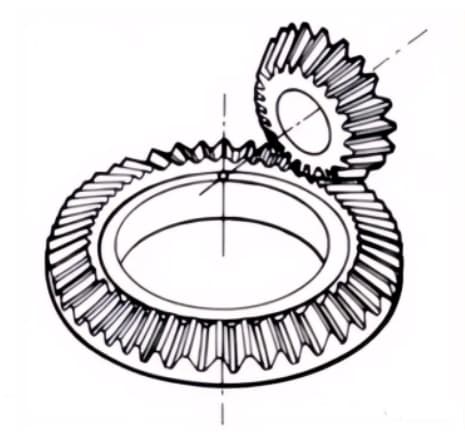
1.ウォームギアペア
ウォームギヤ・ペア」とは、ウォームとそれに噛み合うウォームホイールの組み合わせを指す。ウォームギヤ・ペアの最大の特徴は、1組で大きな変速比が得られ、作動音が静かなことである。しかし、効率が悪いのが欠点である。
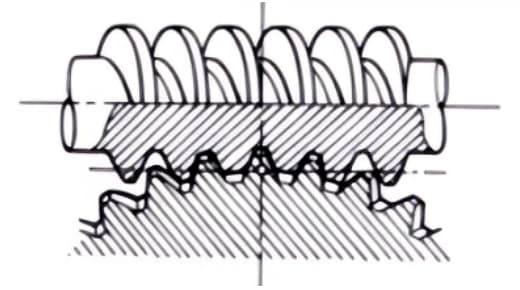
2.ヘリカルギアとウォームギアのペア
円筒ウォームギヤ対を千鳥軸間の伝達用に使用する場合に使われる用語。ヘリカルギヤ対の場合や、ヘリカルギヤ対とスパーギヤ対の間にも使用できる。円滑に作動するが、軽負荷での使用に限られる。
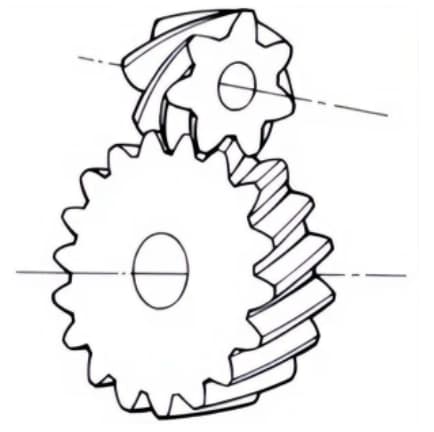
1.フェイスギア
平歯車やはすば歯車とかみ合う円盤状の歯車。直交軸や千鳥軸間の伝達用として使用される。
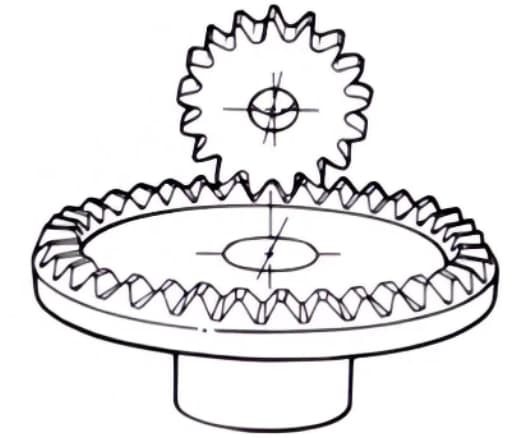
2.アワーグラス ウォームギア ペア
砂時計型ウォームギヤとは、砂時計型ウォームとそれに噛み合うウォームホイールの組み合わせを指す。円筒ウォームギヤに比べて製造が難しいが、大きな荷重を伝達することができる。
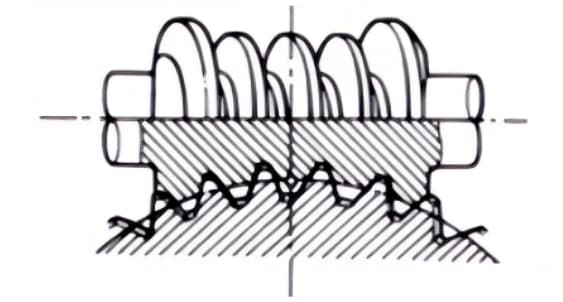
3.ハイポイドギア
千鳥軸間の変速に使われる円錐歯車。スパイラルベベルギアと同じように、大きいギアと小さいギアが偏心して加工されている。噛み合い原理は非常に複雑。
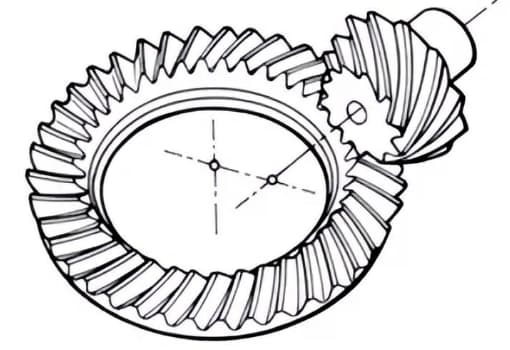
歯車には独特の用語と表現方法があります。ここでは、歯車の理解を深めるために、よく使われる基本的な歯車用語を紹介します。
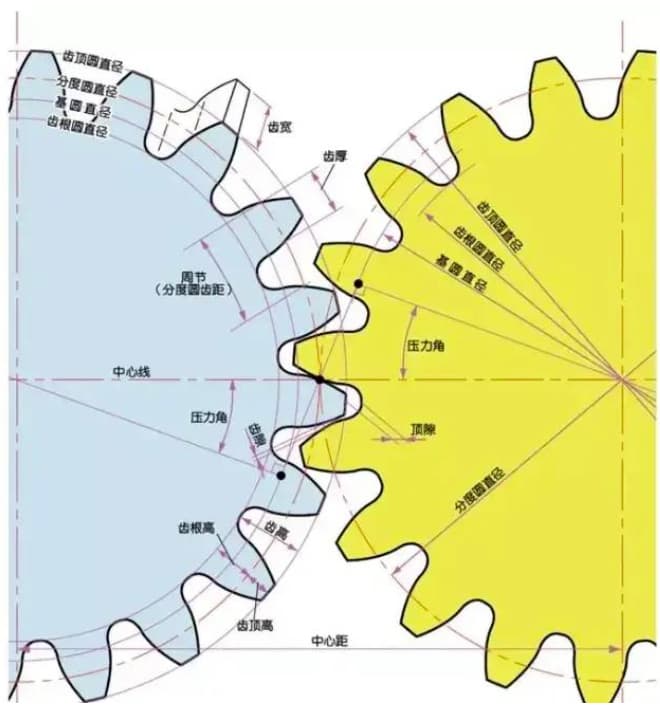
m1、m3、m8...はそれぞれモジュール1、モジュール3、モジュール8と呼ばれます。モジュールは世界共通で使用され、記号m（モジュール）と数字（ミリメートル）で歯の大きさを表します。
数字が大きければ大きいほど、ギアも大きくなる。
アメリカのように帝国単位を使う国では、歯の大きさをDP（直径ピッチ）という記号と数字（直径1インチの歯車の歯数）で表します。
例えばDP24、DP8など。また、CP（円ピッチ）という記号とCP5、CP10といった数字（ミリメートル）を使って歯の大きさを示す比較や特殊な方法もある。
ピッチ（p）は、モジュラスにπを掛けることで求められる。ピッチは隣接する歯間の長さである。
計算式は以下の通り： p= pi x m
各モジュールのティースサイズの比較：
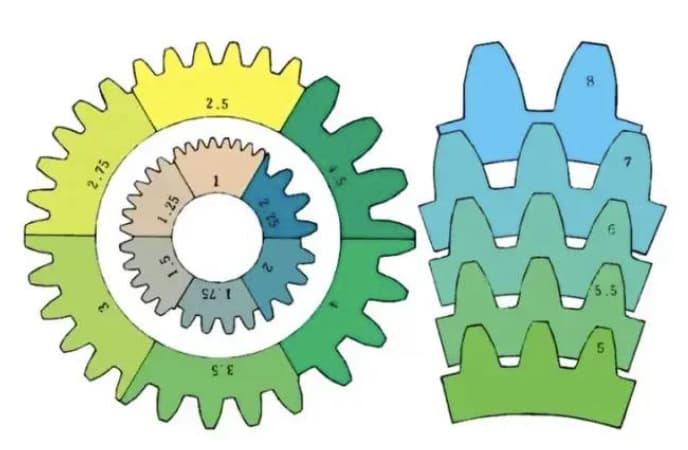
圧力角は、ギアの歯の形状を決定するパラメータです。ギア歯面の傾きを指し、一般的に20度（α）に設定されます。
以前は圧力角14.5度のギアが一般的だった。
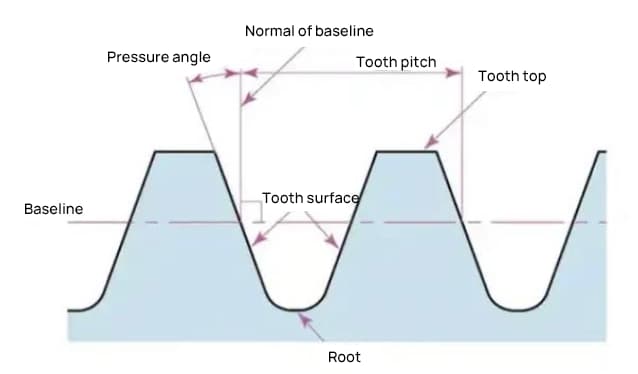
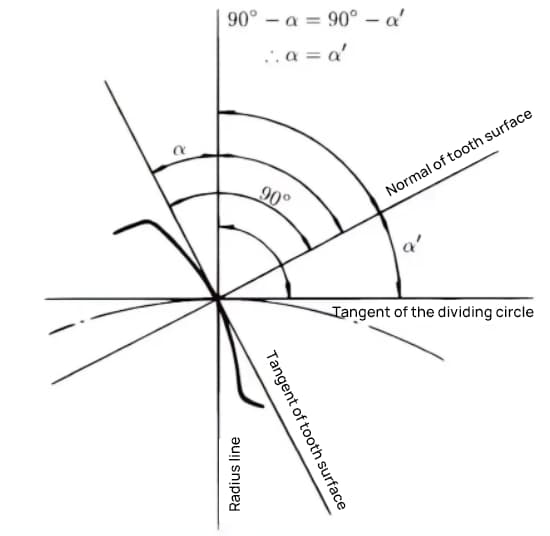
圧力角とは、歯面上の特定の点（一般的には節）における半径と歯形の接線との成す角度のことである。α'＝αなので、α'も圧力角になります。
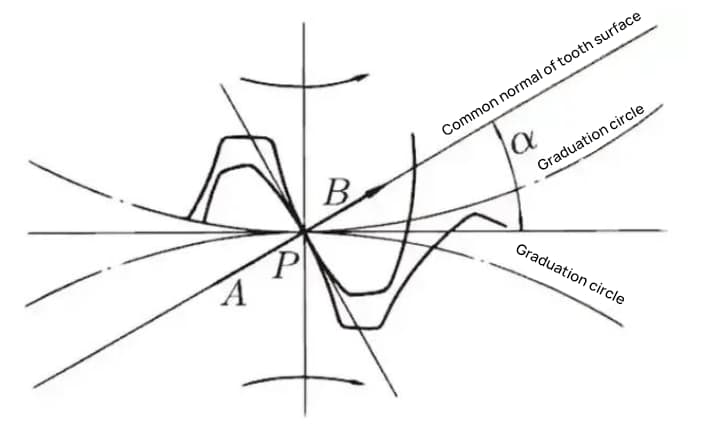
歯車Aと歯車Bのかみ合い状態を節点から見たとき、歯車Aは歯車Bを節点から押します。このとき、駆動力は歯車Aと歯車Bの共通法線に作用します。つまり、共通法線は力の方向であり、圧力軸受けの方向であり、αは圧力角です。
モジュール(m)、圧力角(α)、歯数(z)は歯車の3つの基本パラメータです。これに基づいて、歯車の各部分の大きさが計算されます。
歯車の歯の高さはモジュール（m）によって決まる。
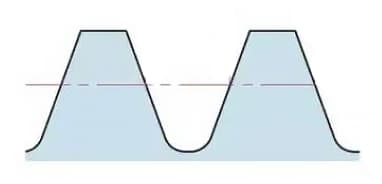
全歯の高さはh=2.25m（＝アディショナルハイト＋デディショナルハイト）。
アディショナルハイト（ha）は、ギヤの歯先からピッチ円までの高さ。
デデンダムハイト（hf）は、ギヤの歯元からピッチ円までの高さ。
歯車の歯の厚さ（s）の基準はピッチの半分である。
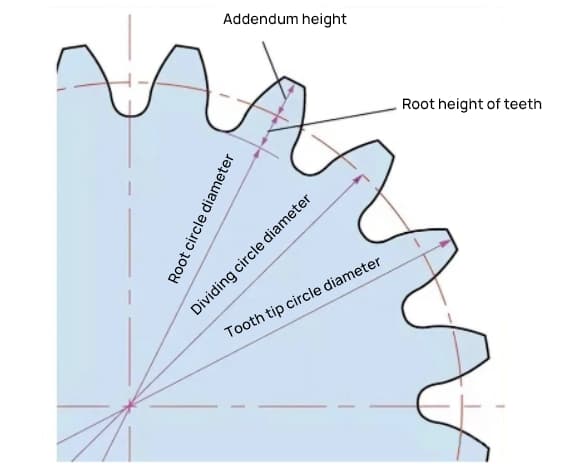
歯車の大きさを決めるパラメータはピッチ円直径(d)です。ピッチ円に基づいて、歯車のピッチ、厚さ、高さ、アデンダム高さ、デデンダム高さを決定することができます。
ピッチ円の直径はd=zmである。
加算円の直径はda=d+2mである。
控除円の直径はdf=d-2.5mである。
ピッチサークルは、ギアのサイズを決定するために使用される想定サークルであるため、実際のギアで直接見ることはできない。
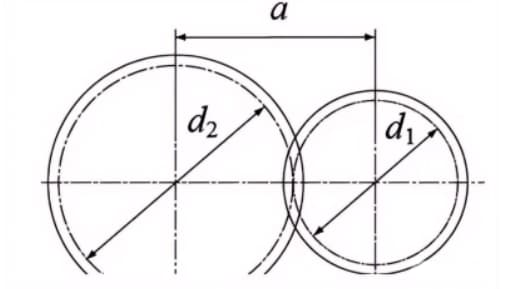
一対の歯車のピッチ円が接線方向にかみ合うと 中心距離 はピッチ円直径の和の半分である。
中心距離a=(d1+d2)/2
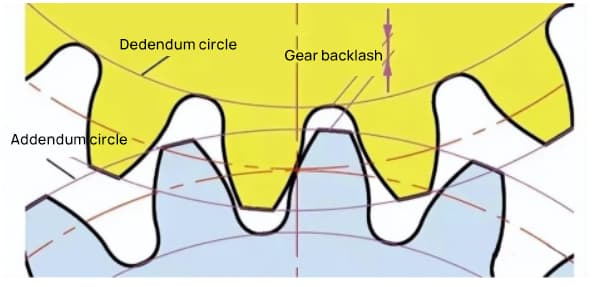
バックラッシは、かみ合い時に歯車のスムーズなかみ合いを得るための重要な要素である。一対の歯車がかみ合ったときの歯面間の隙間のことです。
ギヤの歯の高さ方向にもクリアランスがあります。このクリアランスは軸方向クリアランスまたはクリアランス(c)と呼ばれます。クリアランス(c)は、歯車の歯元円径と相手歯車の歯先円径の差です。
クリアランス c=1.25m-1m=0.25m
平歯車の後に歯がらせん状にねじれた歯車をヘリカルギアと呼ぶ。スパーギヤの幾何学計算のほとんどは、ヘリカルギヤにも適用できます。ヘリカルギヤには、基準面によって2つのタイプがあります：
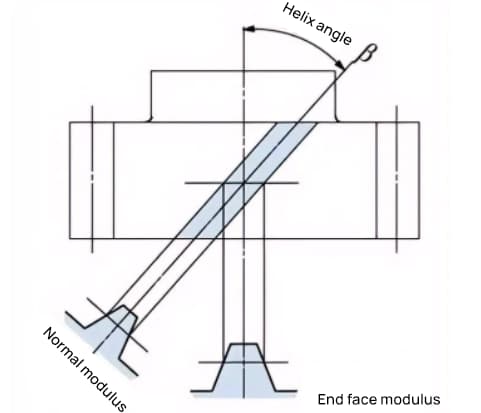
ヘリカルギヤやサイクロイドギヤのように、歯がヘリカル形状になっている歯車は、ヘリカル方向とかみ合いが固定されています。
螺旋方向とは、歯車の軸が上下を向いているとき、歯の向きが正面から見て右上を「右回り」、左上を「左回り」といいます。各種歯車のかみ合わせを以下に示す。
等間隔に配置された歯が、摩擦車の外周部だけを仕切って突起を設け、互いに噛み合わせて回転させると、次のような問題が生じることがある：
歯車伝達が静かで滑らかである必要がある場合、インボリュート曲線が使用される。
インボリュート曲線とは、円柱の外周に鉛筆でワイヤーを巻き、緊張した状態で徐々にワイヤーを離すことで得られる曲線のこと。
鉛筆が描く曲線はインボリュート曲線であり、円柱の外周は底円と呼ばれる。
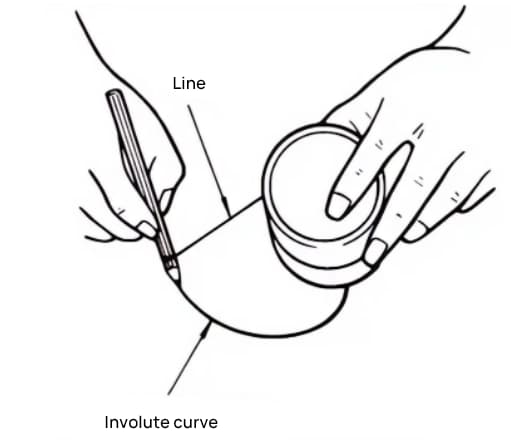
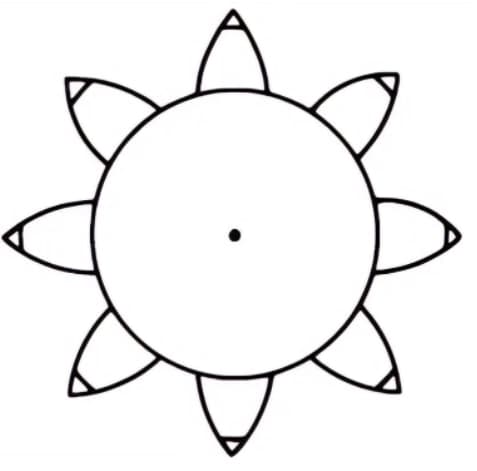
円柱を8等分し、8本の鉛筆を結びつけて8本のインボリュート曲線を描く。次にワイヤーを逆方向に巻き、同じ方法でさらに8本の曲線を描く。これがインボリュート曲線を歯形とする8枚歯の歯車である。
インボリュート歯車の利点は、一定の速度比を伝達できること、接触パターンが徐々に変化するため滑らかに動作すること、中心距離の変動に敏感でないことなどが挙げられる。
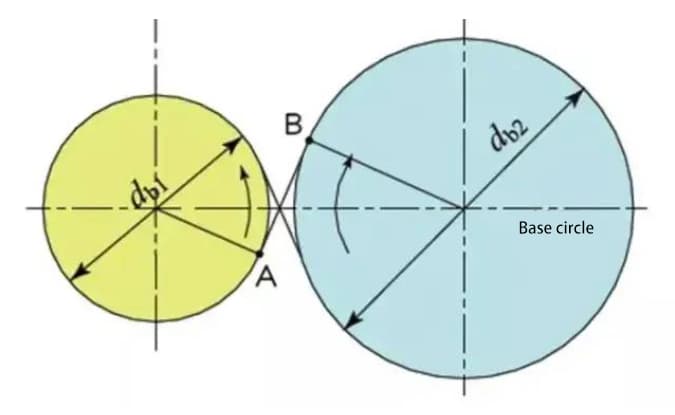
ベース円はインボリュート歯形を形成する基本円です。ピッチ円は歯車の大きさを決める基準円です。ベース円とピッチ円は歯車の重要な幾何学的寸法です。
インボリュート歯形は、ベース円の外側に形成される曲線であり、ベース円の圧力角はゼロである。
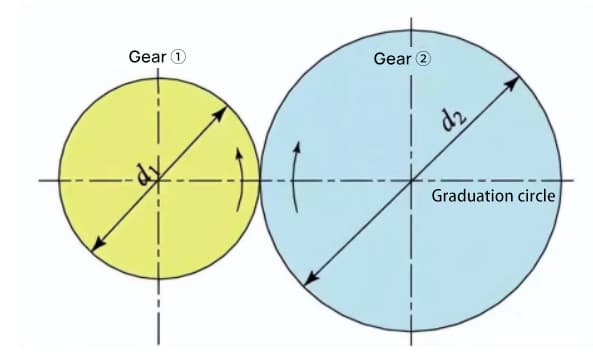
つの標準インボリュート歯車をかみ合わせると、そのピッチ円は標準中心距離で接する。2つの歯車のかみ合いの様子は、それぞれ直径d1とd2の2つの摩擦車の伝達のように見える。
しかし、インボリュート歯車のかみ合いは、実際にはピッチ円ではなくベース円に依存する。
2つの歯車の噛み合う歯の接点は、P1、P2、P3の順に作用線に沿って移動する。
ドライビングギアの黄色い歯に注目してください。この歯が噛み合い始めてから、歯車は一定時間2歯噛み合い（P1、P3）の状態になります。噛み合いが継続し、接点がピッチ円上の点P2に移動すると、1歯だけが噛み合った状態になります。
噛み合いは継続され、接点が点P3に移動すると、次の歯車の歯が点P1で噛み合い始め、再び2枚歯の噛み合い状態を形成する。このように、歯車の2枚歯噛み合いと1枚歯噛み合いは相互に作用し、回転運動を繰り返し伝達する。
基準円A-B間の共通接線を作用線と呼ぶ。歯車対の接点はすべてこの作用線上にある。
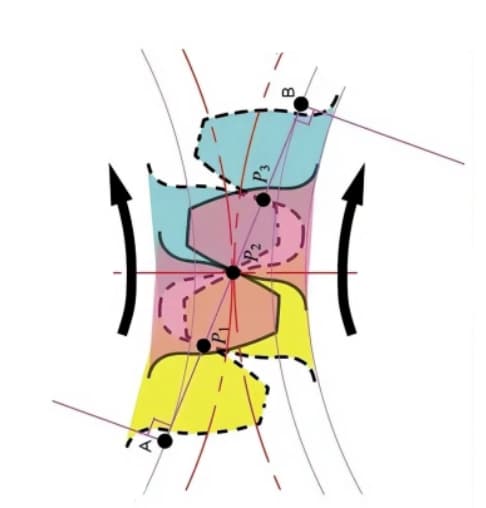
例えるなら、2つのベースサークルの外周を走るベルトのようなもので、回転運動によって動力を伝達する。
私たちが通常使用するギアの歯形は、一般的に標準的なインボリュートですが、中心距離を調整したり、小さいギアのアンダーカットを防ぐなど、ギアの歯をずらす必要がある状況もあります。
インボリュート歯形曲線は歯の数によって変化する。歯の数が多ければ多いほど、歯形曲線は直線に近づく傾向がある。
歯の数が増えると歯根の形状が太くなり、歯車の強度が増す。
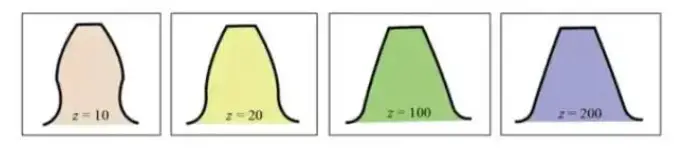
上のグラフから、歯数10の歯車の場合、歯元のインボリュート歯形の一部が削られ、アンダーカットになることがわかります。
しかし，z=10のギヤを正変位とし，加算円の直径を大きくし，ギヤ歯の歯厚を厚くすることで，200歯のギヤと同等のギヤ強度を得ることができる．
下図は、正変位10歯ギヤの模式図です。歯切りの際，半径方向に沿って工具が移動する量を半径方向移動量（変位量と呼ぶ）xm(mm)という．
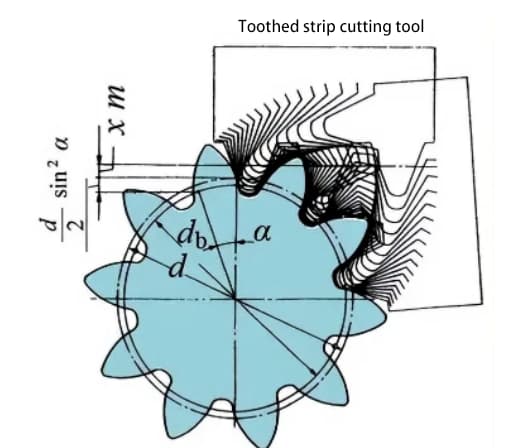
歯形が正方向に変位することで、ギアの歯厚が増加し、外径（加算円径）も増加します。
積極的な変位を採用することで、ギアのアンダーカットを避けることができます。歯車の変位は、中心距離を変えるなど、他の目的も達成することができます。正変位は中心距離を大きくすることができ、負変位は中心距離を小さくすることができます。
正変位、負変位にかかわらず、変位量には限界がある。
変位はプラスにもマイナスにもなる。歯の高さは同じですが、歯の厚さが違います。歯厚が厚い歯車は正変位歯車で、歯厚が薄い歯車は負変位歯車です。
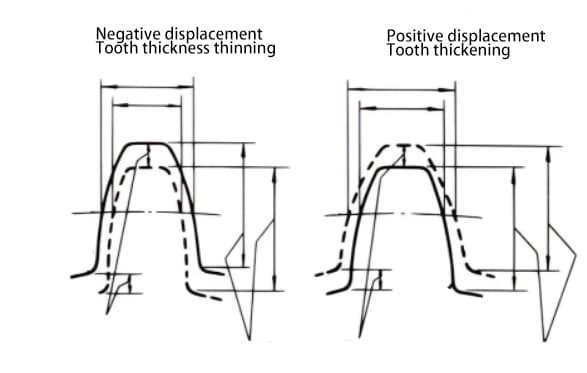
2つのギヤの中心距離を変えることができない場合、同じ中心距離にするために、小さい方のギヤに正の変位を与え（アンダーカットを避けるため）、大きい方のギヤに負の変位を与えることができる。この場合、変位量の絶対値は等しくなります。
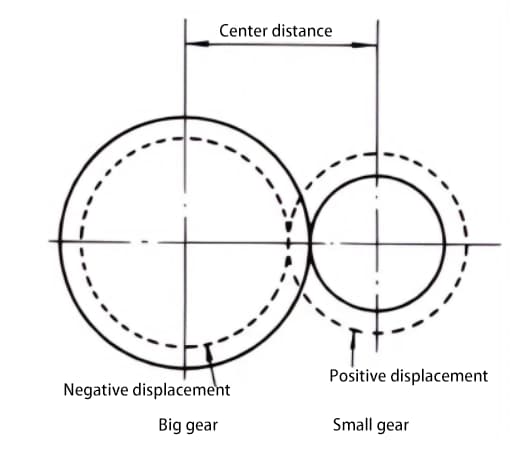
標準的な歯車は、ピッチ円が互いに接するときにかみ合う。変位歯車のかみ合いは、図のように、かみ合い円上で互いに接する。
噛み合い円の圧力角を噛み合い角という。噛み合い角は、ピッチ円圧力角（ピッチ円圧力角）とは異なり、変位歯車の設計において重要な要素である。
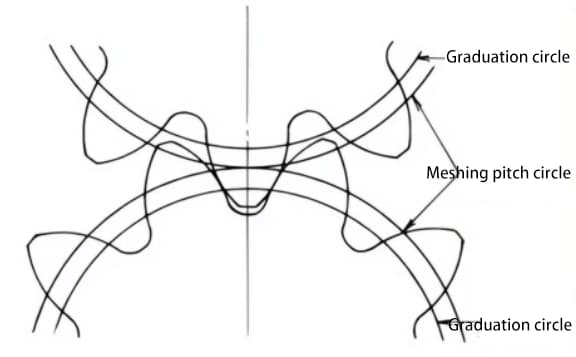
歯車の変位は、加工中の少ない歯数によるアンダーカットを防ぐことができます。また、変位により所望の中心距離を得ることができます。
歯数の差が大きい一対の歯車では、摩耗しやすい小さい方の歯車に正の変位を与えて歯厚を厚くし、大きい方の歯車に負の変位を与えて歯厚を薄くすることで、2つの歯車の寿命を同等にすることができる。
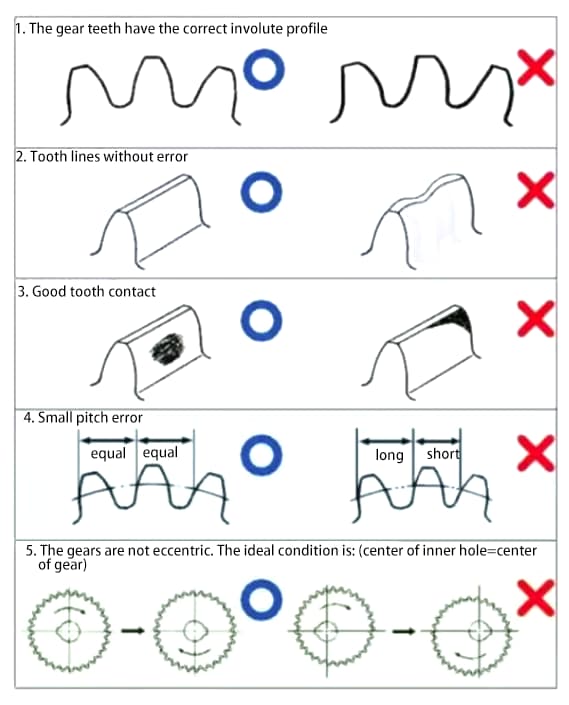
歯車は動力と回転を伝達する機械部品である。歯車の性能に必要な主な条件は以下の通りです：
上記の要求を満たすためには、歯車精度の向上が必須課題となる。
歯車の精度は大きく3つに分けられる：
a) インボリュート歯形の精度 - 歯形精度
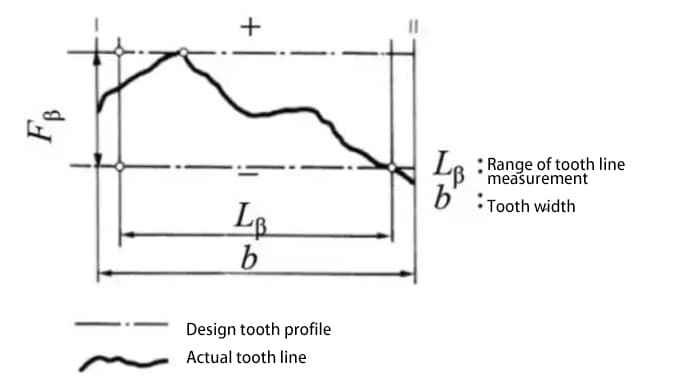
b) 歯面上の歯すじ精度 - 歯すじ精度
c) 歯とスロットの位置の精度。
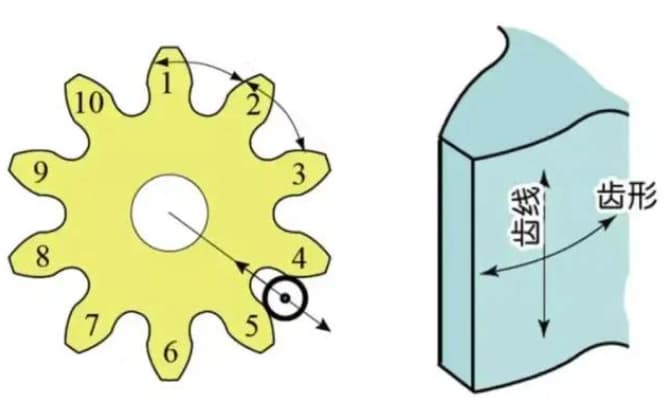
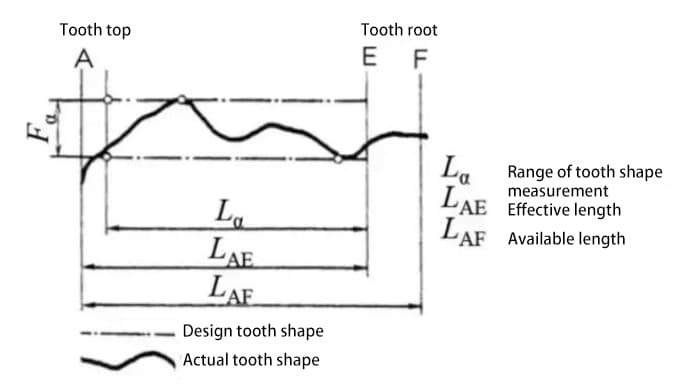
歯形誤差とは、実際の歯車の歯形と理論上の歯形との誤差のことです。
歯形誤差には、工具や切削加工中の工作機械の振動など、さまざまな要因が影響する。
歯形誤差は，歯車のかみ合い性能と騒音に影響する．そのため、歯形誤差を許容範囲内に制御する必要があります。
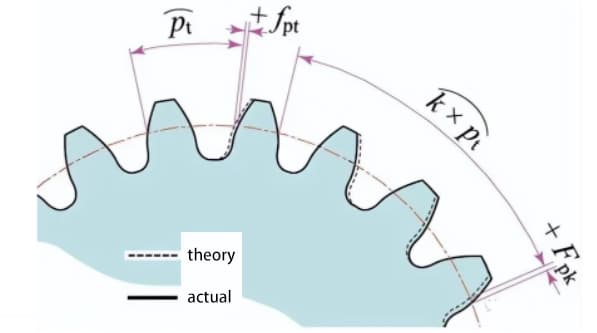
ギヤシャフトを中心とした測定円周上でピッチ値を測定する。
単歯ピッチ偏差（fpt）とは、実際のピッチと理論上のピッチの差。
ピッチ累積偏差(Fp)は，歯車全体のピッチの偏差を評価するために使用します．ピッチ累積偏差曲線の振幅の合計値がピッチ全体の偏差を表します。
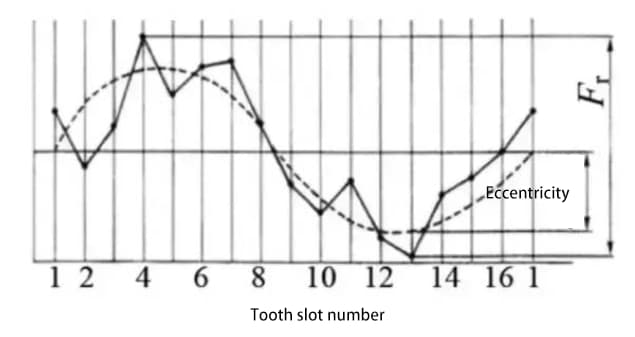
プローブ（球形または円筒形）を歯溝に連続して入れ、プローブからギア軸までの半径方向の最大距離と最小距離の差を測定します。ギア軸の偏心はラジアル振れの要因の一つです。
これまで述べてきた歯車の精度を評価する方法は、歯形精度、ピッチ精度、歯面精度など、いずれも歯車単体の精度を評価する方法でした。
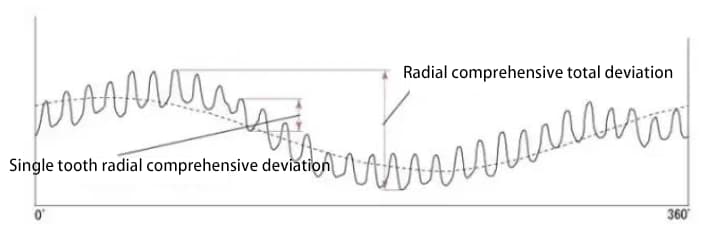
これに対して、測定歯車と組み合わせて歯車の2歯かみ合い試験を行い、歯車の精度を評価する方法もあります。試験ギヤの2つの面が測定ギヤと噛み合い、1サイクル回転します。中心距離の変化が記録されます。
下図は 30 歯の歯車の試験結果です。1歯のラジアル合成偏差には合計30本の波線があります。
ラジアル合成偏差の値は、ラジアル振れ偏差と単歯ラジアル合成偏差のほぼ合計である。
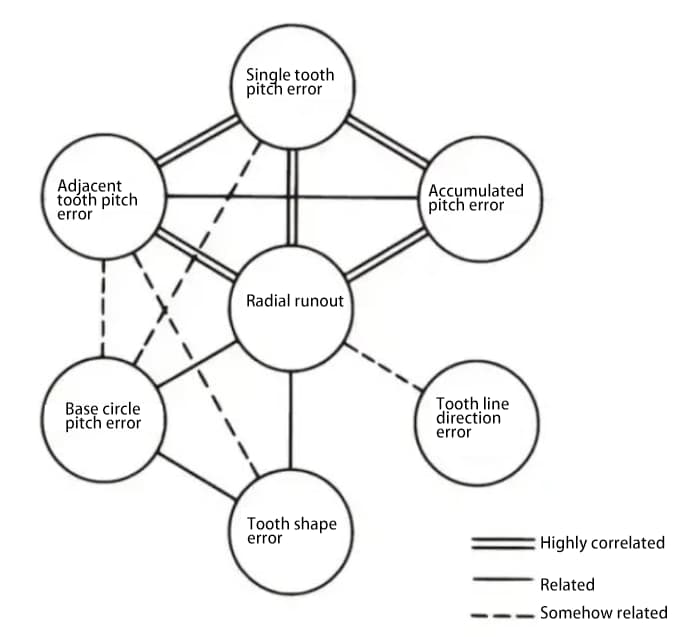
歯車精度の様々な部分は互いに関連しています。一般的にラジアル振れは他の誤差と強い相関関係があり、また様々なピッチ誤差の間にも強い相関関係があります。
通常の円筒形断面の螺旋角度：
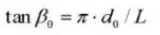
ベースシリンダー上のスパイラルアングル：
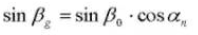
歯厚の中心角：
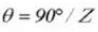
ピンの直径：
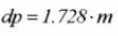
中心距離補正係数：
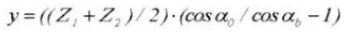
標準平歯車（ピニオンギヤ①、ギヤホイール②）の計算
1.歯車の標準歯数
2.標準インボリュート歯車プロフィール 直歯歯車
3.モジュール m
4.圧力角度
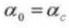
5.歯の数
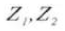
6.有効歯の深さ
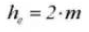
7.歯の深さ全体
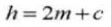
8.コグクリアランス
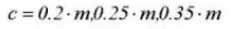
9.基準ピッチ円直径
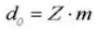
10.外径
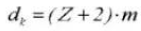
11.ルート径
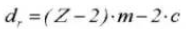
12.ベース円直径
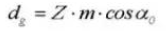
13.円形ピッチ
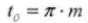
14.通常の直径ピッチ
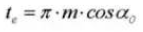
15.円形歯厚
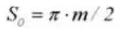
16.脊索歯厚
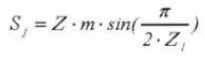
17.ギアオイル・ディップスティックの歯の高さ
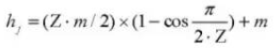
18.全体の歯の数
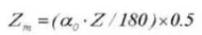
19.歯の厚さ
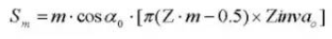
20.ピンの直径
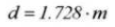
21.円筒測定寸法
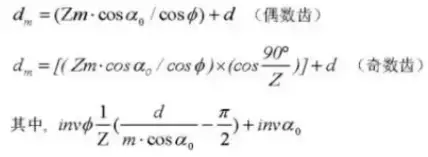
平歯車の変位計算式（ピニオン①、ギヤ②）：
1.歯車の歯形
2.工具歯形接触率
3.モジュール m
4.圧力角度
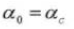
5.歯数 Z
6.有効歯の深さ
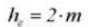
7.歯の深さ全体
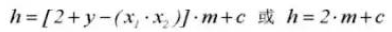
8.ギヤバックラッシ C
9.横コンタクト比 X
10.中心距離
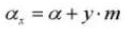
11.基準ピッチ円直径
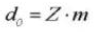
12.作動圧力角度
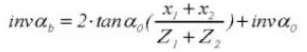
13.ピッチ円直径
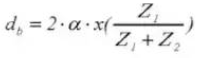
14.外径
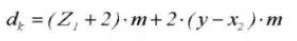
15.補遺直径
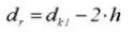
16.ピッチ径
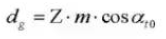
17.円形ピッチ
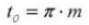
18.ノーマル直径ピッチ
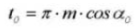
19.円形歯厚
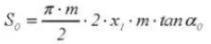
20.脊索歯厚
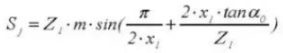
21.ギアバーニアキャリパーの歯の高さ
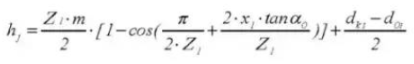
22.全体の歯の数
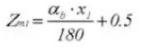
23.歯の厚さ
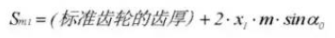
24.先端直径
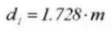
25.横断測定寸法
標準はすば歯車(ノーマル系)の計算式(ピニオン①、ギヤ②)
1.ギア歯形規格
2.歯型ノーマルシステム参考編
3.工具歯形ヘリカルギア
4.モジュール
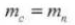
5.圧力角度
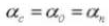
6.歯の数
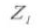
7.らせんの方向
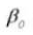
8.有効歯の深さ
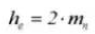
9.歯の深さ全体
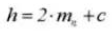
10.フロント・プレッシャー・アングル
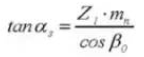
11.中心距離
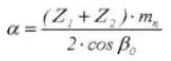
12.基準ピッチ円直径
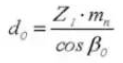
13.外径
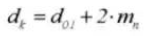
14.根の直径
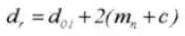
15.ピッチ径
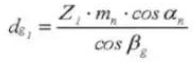
16.ベース円上の螺旋角度
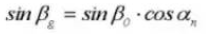
17.ピッチ
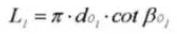
18.円ピッチ（ノーマルシステム）
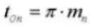
19.ノーマル直径ピッチ（ノーマルシステム）
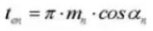
20.円形歯厚（ノーマルシステム）
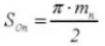
21.標準平歯車の等価歯数
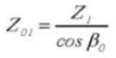
22.脊索歯厚
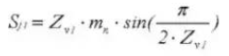
23.ギヤバーニアキャリパーの歯の深さ
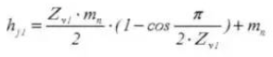
24.全体の歯の数
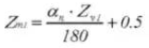
25.歯の厚さ
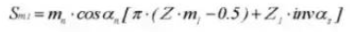
26.先端直径
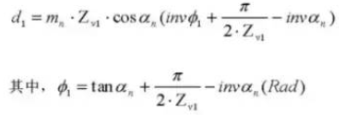
27.円筒測定寸法
28.ギアのバックラッシュ f
ヘリカルギヤ（ノーマルシステム）の変位計算式（ピニオン①、ギヤ②）：
1.歯車の歯形がずれる
2.歯型ノーマルシステム参考編
3.工具歯形ヘリカルギア
4.モジュール（ノーマルシステム）
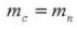
5.圧力角（ノーマルシステム）
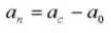
6.歯の数
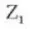
7.らせんの方向
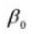
8.有効歯の深さ
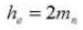
9.歯の深さ全体
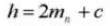
10.横方向の接触比
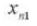
11.中心距離
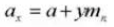
12.ノーマルモジュール
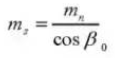
13.フロント・プレッシャー・アングル（ノーマル・システム）
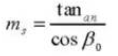
14.標準平歯車の等価歯数
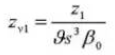
15.通常のシステム圧力角度
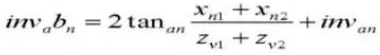
16.基準ピッチ円直径
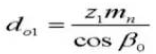
17.外径
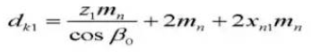
18.接触する歯のピッチ径
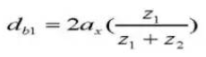
19.ピッチ径
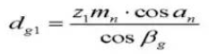
20.ベースシリンダーの螺旋角度
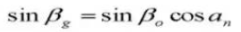
21.円形歯厚
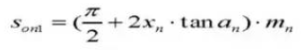
22.脊索歯厚
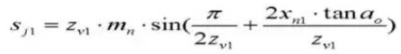
23.ギア・バーニア・キャリパーの歯の高さ。
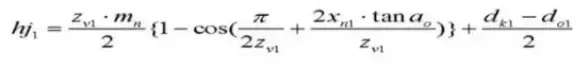
24.全体の歯の数
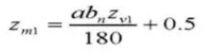
25.歯の厚さ
26.ピンの直径。
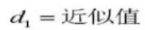
27.円筒測定寸法
MachineMFGの創設者として、私は10年以上のキャリアを金属加工業界に捧げてきました。豊富な経験により、板金加工、機械加工、機械工学、金属用工作機械の分野の専門家になることができました。私は常にこれらのテーマについて考え、読み、執筆し、常にこの分野の最前線にいようと努力しています。私の知識と専門知識をあなたのビジネスの財産にしてください。
JA 
EN 
AR 
DE 
ES 
FR 
IT 
NL 
PT 
RU