ギア素材の選択：考慮すべき重要な要素
適切なギア材質を選択することは、なぜエンジニアリングにおいて非常に重要なのでしょうか？適切な材料を選択することで、歯車は耐摩耗性、耐久性、効率などの要求を満たすことができます。この記事では、様々な歯車材料について説明します。
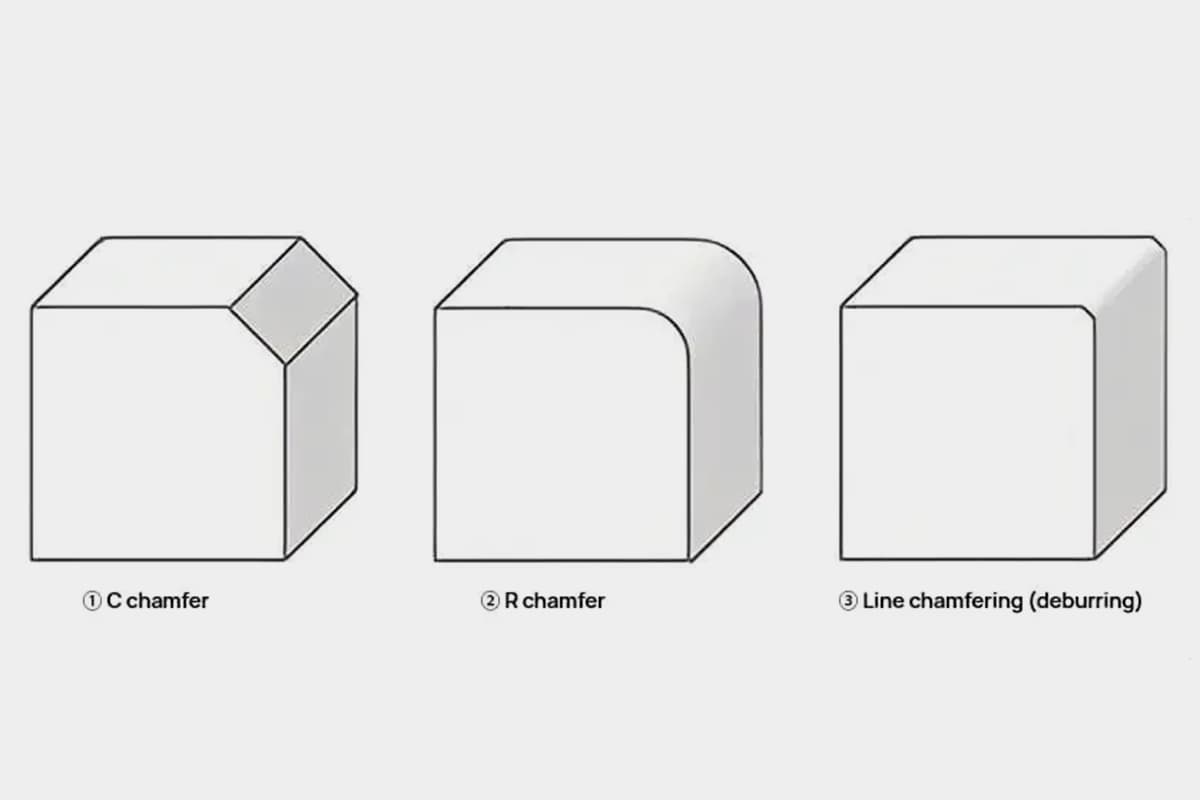
製造業において、エンジニアがどのようにして精度と正確さを確保しているのか、不思議に思ったことはありませんか？このブログでは、高品質な部品の製造を可能にする機械工学の重要な側面である幾何公差の魅力的な世界を掘り下げていきます。経験豊富なプロフェッショナルの専門知識から、さまざまな種類の公差とその用途を探り、この複雑なテーマに対する理解を深めるための貴重な洞察を提供します。機械工学の領域で完璧を達成するための秘訣を発見してください！
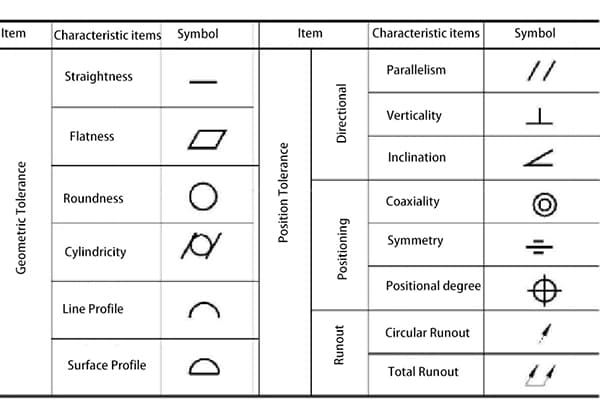
国家規格で規定されている幾何公差は、幾何公差と位置公差の2つに分けられ、合計14項目ある。
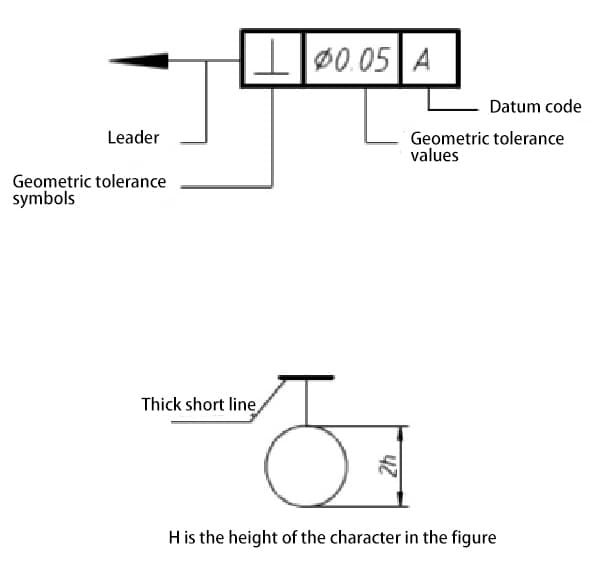
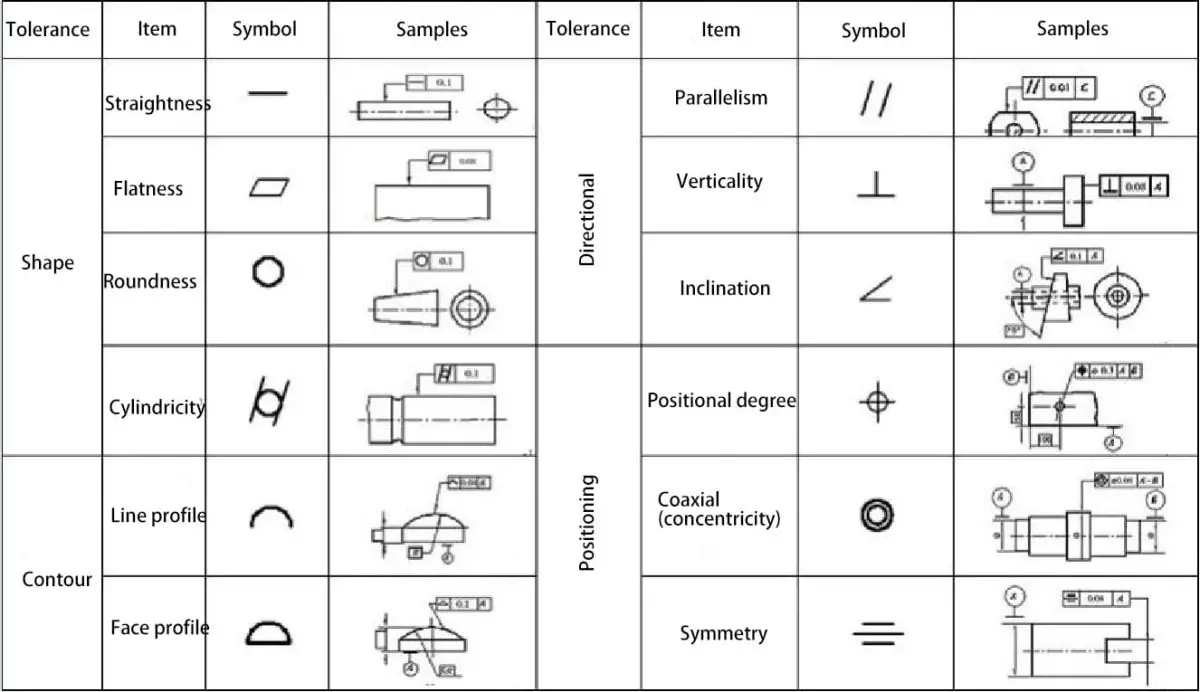
それぞれの名称と記号を下表に示す。
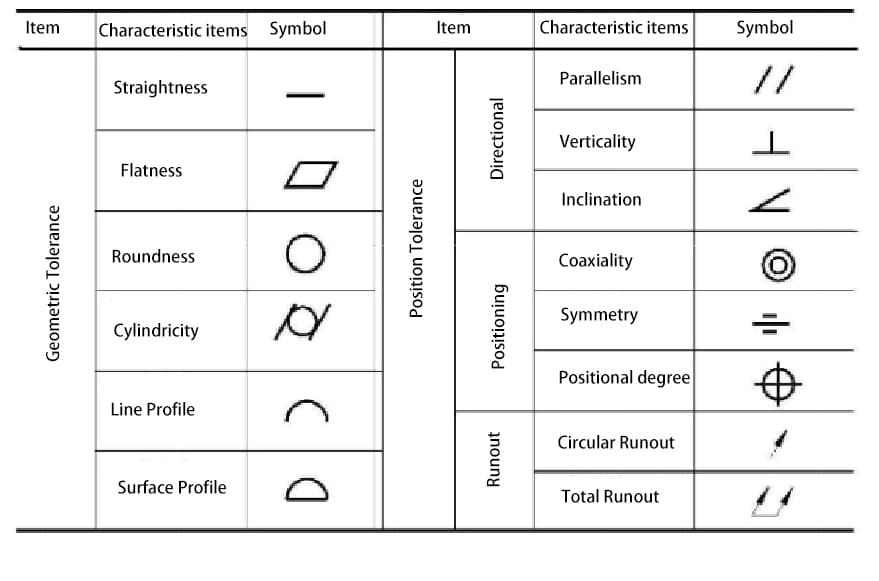
真直度 - すべての点は直線上にあり、公差は2本の平行線の間の領域で指定される。
平坦性 - サーフェス上のすべての点は平面上にあり、2つの平行な平面の間の領域によって公差が指定される。
丸み - サーフェス上のすべての点は円周上にあり、公差は2つの同心円の間の領域で指定される。
円筒度 - 回転面上のすべての点の軸は、共通の軸から等距離にある。円筒度公差は、2つの同心円筒によって形成される公差領域を定義し、この回転面はこの領域内に収まっていなければならない。
プロフィールの許容範囲 - 不規則なサーフェス、ライン、円弧、または通常の平面の公差方法を定義します。プロファイルは、単一の線要素または部品のサーフェス全体に適用できます。プロファイル公差は、実際のプロファイルに沿った固有の境界を指定します。
垂直性 - 面または軸が基準面または軸に垂直であること。垂直トレランスは、データム平面または軸に垂直な2つの平面によって定義される領域、またはデータム軸に垂直な2つの平行平面によって定義される領域のいずれかを指定します。
パラレリズム - 面または軸とすべての点が基準面または軸から等距離にある。 並列度許容度 は、データム平面または軸に平行な2つの平行平面または直線で定義される領域、または軸がデータム軸に平行な円筒度許容領域、のいずれかを指定する。
同軸性 - 回転サーフェスのすべての交差する組み合わせ可能要素の軸は、データフィーチャの共通軸である。同軸度公差は、軸がデータム軸と同じである円筒度公差領域を指定する。
ポジション公差 - 位置公差は、中心軸または中心平面が実際の（理論的に正しい）位置からずれることが許される領域を定義する。
基本寸法は、データ特徴と相互に関連する特徴との間の実際の位置を確立する。位置誤差は、フィーチャーとその正しい位置との間の許容可能な位置偏差の合計である。
穴や外径のような円筒形フィーチャーの場合、位置公差は通常、フィーチャーの軸が入るべき公差領域の直径となる。非円形フィーチャ（スロットや短い突起など）の場合、位置公差は、フィーチャの中心面が落下しなければならない公差領域の全幅となる。
円形振れ - 円形サーフェス要素に対する制御を提供します。部品が360度回転すると、この公差は円形要素の任意の測定位置で独立して適用され、基準軸の周りに構築された円形振れ公差に適用され、真円度と同軸度の累積変化を制御します。
データム軸と垂直に構成されたサーフェスに適用すると、平面サーフェスフィーチャーの円形要素を制御する。
総振れ - すべてのサーフェス要素の複合制御を提供します。部品が360度回転する場合、この公差は円形と細長い形状の両方に同時に適用されます。基準軸を中心に構成されるサーフェスに適用される場合、総合振れは真円度、円筒度の累積変動を制御します、 真直同軸度、角度、テーパー、プロファイル。データム軸と垂直に構成されたサーフェスに適用すると、サーフェスのばらつきの累積を制御する。 矩 そして真直さ。
Feature - コンポーネントのジオメトリを構成する点、線、面を指す。
理想的な特徴 - 幾何学的な意味を持つ特徴。
実際のフィーチャ - コンポーネント上に実際に存在するフィーチャ。
基準フィーチャ - 測定フィーチャの方向または位置を決定するために使用されるフィーチャ。単に基準と呼ばれ、フィーチャ間の幾何学的関係を決定するための基礎となる。基準点、基準線、基準面などがある。
測定フィーチャ - 形状または位置の公差を指定するフィーチャ。
中心フィーチャー - フィーチャーと対称的な関係にある点、線、面。
許容範囲 - 実際の形状や位置の特徴の変動を制限する。サイズ、形状、方向、位置によって決定される、所定の最大誤差値によって定義される領域である。"
公差帯域とは、2本の平行な直線／平面／円柱などの間の、公差値t
例1
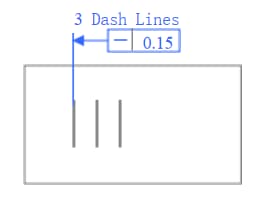
各彫刻線は、公差値0.015mmで表面の2本の平行線の間に位置しなければならない。
例2
円筒面上の任意の要素線は、軸方向面内で、公差値0.02mmの距離にある2本の平行線の間に位置しなければならない。
使用例
例3
円筒面上の任意の要素線は、軸方向平面内かつ2本の平行線の間に、100mmの範囲内で0.04mmの公差値で配置されなければならない。
例4
ディスカッション同じサーフェス上の2つの方向で異なる真直度公差が与えられている場合、どのように理解すべきでしょうか？
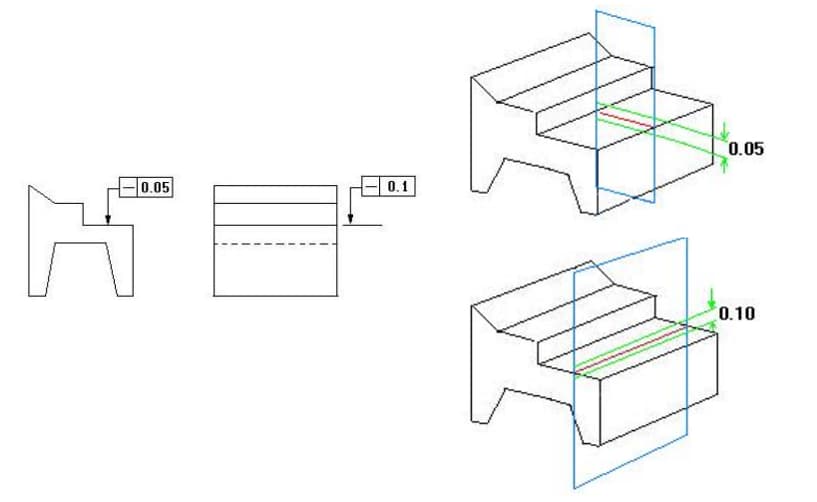
公差帯は、公差値tの距離にある2つの平行な平面の間の領域である。
これは、理想的な平面条件を保持するコンポーネントの平面形状の実際の形状を表します。
例1
上面は、公差0.1mmで2つの平行面内に位置しなければならない。
例2
表面上の任意の100×100の範囲は、公差値0.1mmで2つの平行平面内に位置しなければならない。
これは、コンポーネント上の円形フィーチャーの実際の形状を表し、その中心は等しい距離を保つ。
公差帯とは、同一断面上で公差値tの半径差を持つ2つの同心円の間の領域である。
例1
軸に垂直な任意の断面において、公差値0.02mmの半径を持つ2つの同心円の間に円が位置していなければならない。
例2
軸に垂直な任意の断面において、公差値0.02mmの半径を持つ2つの同心円の間に円が位置していなければならない。
これは、部品上の円筒面の輪郭上のすべての点が、その軸から等しい距離を保つ状態を表す。
公差帯とは、同一軸上で、公差値tの半径差を持つ2つの円筒面の間の領域である。
例1
円筒面は、同一軸上に公差値0.05mmの半径差を持つ2つの円筒面の間に位置しなければならない。
実際に測定された部品の形状が、基準から等しい距離を保っている状態を表す。
一方向が与えられた場合、公差帯は、公差値tの距離で、基準面（または線、軸）に平行な2つの平行面の間の領域であり、垂直な2方向が与えられた場合、公差値t1×t2の寸法で、基準軸に平行な直方体内の領域である。
例1
上面は、公差値0.05mmの距離にある2つの平行な平面の間に位置し、基準面に平行でなければならない。
例2
ΦDの軸は、公差値0.1mmの距離にある2つの平行な平面の間に位置し、基準軸Φと垂直に平行でなければならない。
この公差は、部品上の実際のフィーチャーが基準フィーチャーに対して正しい90度の角度を保っている状態を表します。
方向が与えられたとき、公差領域は、基準平面（または直線、軸）に垂直で、公差値tに等しい距離だけ離れた2つの平行平面（または直線）の間の領域である。
互いに垂直な2つの方向が与えられている場合、公差領域は、基準軸に垂直な寸法t1×t2の平行六面体の内側の領域である。
例1
右面は、基準面に対して垂直で、偏差が0.05mmである2つの平行面の間に位置していなければならない。
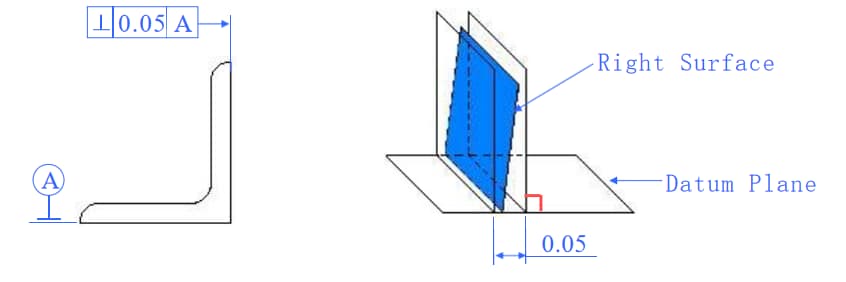
例2
左側面は、0.05mmの偏差範囲内にあり、基準軸に垂直な2つの平行面の間になければならない。
例3
シリンダーdの軸は、直径公差0.05mmで基準面に垂直なシリンダー表面内に位置しなければならない。
例4
円孔Eの軸は、基準面Zに垂直な2つの平行面の間に、偏差値0.06mmで存在しなければならない。
部品上の2つの要素の相対的な方向が所定の角度を保っている正しい状態。
指定された方向内では、公差領域は、データム面（または線または軸）に対して理論的に正しい角度を持ち、そこから公差値tの距離にある2つの平行な面（または線）の間の領域である。
例1
傾斜面は、基準面に対して45度の角度をなし、基準面から0.08mmの距離にある2つの平行な平面の間に、許容範囲内で配置されなければならない。
例2
フィーチャー D の軸は、データム軸に対して 45 度の角度を持ち、公差ゾーン内でデータム軸から 0.1mm の距離にある 2 つの平行平面の間に位置しなければならない。
同心度とは、部品の測定軸がデータム軸と同一直線上のアライメントを維持する状態をいう。
トレランスゾーンは、トレランス値tの直径を持ち、データム軸と同軸の円筒内の領域である。
例1
フィーチャ D の軸は、直径 0.1mm の円柱内に位置し、公差ゾーン内でデータム軸 D と同軸でなければならない。
対称性とは、部品上の2組の対称的な特徴が同一平面上に並んでいる状態をいう。
公差領域は、データム中心面（または中心線、軸）から公差値tの距離にあり、データムに対して対称に配置された2つの平行な面（または線）の間の領域である。
互いに垂直な2つの方向が指定された場合、トレランスゾーンは、断面がトレランス値t1 x t2に等しい4角柱内の領域となる。
例1
スロットの中心面は、データム中心面に対して対称に配置された2つの平行な平面の間に位置し、公差範囲内でそこから0.1mmの距離になければならない。
例
(1) 端子の中心をまっすぐにすること。
(2) スロットの中心からの片側の最大偏差は、0.035mm を超えてはならない。
質問は？
(1) オフセットTの計算方法は？
T=(b-a)/2
(2) 対称性の許容範囲は？
位置公差とは、部品上の点、線、面、その他の要素の理想的な位置に対する精度を指す。
許容範囲：
(1) 点の位置公差：点の位置公差：点の理想位置を中心とした、公差値 t の直径を持つ円または球内の領域を公差領域とする。
(2) 線の位置公差：方向が与えられている場合、公差領域は、線の理想位置を中心に対称に配置され、公差値tの距離にある2つの平行な平面（または線）の間の領域である。垂直な2つの方向が与えられている場合、公差領域は、断面の大きさがt1×t2の4角柱内の領域であり、プリズムの軸線は線の理想位置に一致する。
(3) サーフェスの位置公差：公差領域は、サーフェスの理想位置を中心に対称に配置され、公差値tの距離にある2つの平行平面の間の領域である。
例1
その点は、公差値0.3mmの直径を持つ円内に位置し、円の中心が相対データムAとBで決定される点の理想的な位置になければならない。
3データムプレーンシステム：
互いに垂直な3つのデータム面A、B、Cは、データム面システムを構成し、一般に3データム面システムとして知られている。部品上の様々な要素の幾何学的関係を決定するための出発点である。
3データムプレーンシステムでは、データムプレーンはその機能によって並べられている。
最も重要なのは第1基準面（A）で、第2基準面（B）、第3基準面（C）と続く。
例2
穴の軸線は公差値0.1mmの円柱面内に位置しなければならず、円柱面の軸線は相対データムA、B、C上の点の理想的な位置に一致しなければならない。
例3
コンポジットの位置公差。
幾何学的なフレーム：
これは、理想的な軸線のセット間、または軸線とデータム間の正しい幾何学的関係を示す図形である。
4つのDホールの軸は、直径公差値0.1mmと直径公差値0.05mmの2つの円筒形公差ゾーンの重なり部分内に位置しなければならない。4つの0.1mm位置公差ゾーンの幾何学的フレームは、データムA、B、Cに対して相対的に決定される。4つの0.05mm位置公差ゾーンの幾何学的フレームは、データムAに対してのみ方向付けられる。
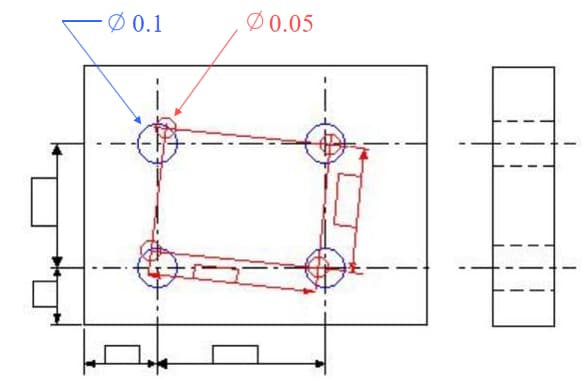
4つのDホールの軸は、直径公差値0.1mmと直径公差値0.05mmの2つの円筒形公差ゾーンの重なり部分内に位置しなければならない。4つの0.1mm位置公差ゾーンの幾何学的フレームは、データムA、B、Cに対して相対的に決定される。4つの0.05mm位置公差ゾーンの幾何学的フレームは、データムAに対してのみ方向付けられる。
考察以下の2種類の位置精度を比較する。
部品の回転面が測定面内に制限され、基準軸に対して所定の位置を維持する状態をいう。
(1) ラジアル方向の振れ。
公差ゾーンは、基準軸上に中心を持つ2つの同心円の間の領域であり、基準軸に垂直な任意の測定平面における半径の差が公差値tとなる。
(2) 端面の振れ。
トレランスゾーンは、基準軸と同軸の任意の直径位置において、測定シリンダー上の幅tを持つ、ジェネレーティブ方向に沿った円筒状の表面領域である。
例1
ラジアル方向の振れ。
円筒面が軸方向に移動することなく基準軸を中心に回転する場合、どの測定面においても半径方向の振れは許容値0.05mmを超えてはならない。
公差ゾーンは、基準軸上に中心を持つ2つの同心円の間の領域であり、基準軸に垂直な任意の測定平面における半径の差が公差値tとなる。
例2
端面の振れ。
部品が軸方向に移動することなく基準軸の周りを回転する場合、左端面のどの測定径でも軸方向の振れは許容値0.05mmを超えてはならない。
トレランスゾーンは、基準軸と同軸の任意の直径位置において、測定シリンダー上の幅tを持つ、ジェネレーティブ方向に沿った円筒状の表面領域である。
基準軸を中心に連続的に回転したときの、部品の測定面全体に沿った均等な振れを指す。
(1) ラジアル方向の総振れ。
トレランスゾーンは、基準軸と同軸で、半径がトレランス値t
(2) 端面の総振れ。
トレランスゾーンは、基準軸に垂直で、トレランス値tの距離を持つ2つの平行な平面の間の領域である。
例1
半径方向の総振れ。
インジケータが基準軸に平行に直線的に移動する間に、表面が軸方向に移動することなく基準軸の周りを連続的に回転する場合、表面全体に沿った振れは公差値0.02mmを超えてはならない。
トレランスゾーンは、基準軸と同軸で、半径がトレランス値tの差を持つ2つの円柱の間の領域である。
例2
端面の総振れ。
インジケータが基準軸に対して垂直に直線移動する間に、端面が軸方向に移動することなく基準軸の周りを連続的に回転する場合、端面全体に沿った振れは公差値0.05mmを超えてはならない。
トレランスゾーンは、基準軸に垂直で、トレランス値tの距離を持つ2つの平行な平面の間の領域である。
MachineMFGの創設者として、私は10年以上のキャリアを金属加工業界に捧げてきました。豊富な経験により、板金加工、機械加工、機械工学、金属用工作機械の分野の専門家になることができました。私は常にこれらのテーマについて考え、読み、執筆し、常にこの分野の最前線にいようと努力しています。私の知識と専門知識をあなたのビジネスの財産にしてください。
JA 
EN 
AR 
DE 
ES 
FR 
IT 
NL 
PT 
RU