板金曲げ計算：手当、控除、Kファクター

板金設計の分野において、曲げ代、曲げ控除、Kファクターといった用語は、製造工程の精度と効率に大きく影響する重要な概念です。これらのパラメータは、曲げ板金部品の最終寸法を決定し、正確な加工を保証する上で重要な役割を果たします。これらの概念を深く掘り下げ、その計算方法を探ってみましょう。

1. 板金の計算方法の紹介

板金加工に携わるエンジニアやメーカーは、高度なアルゴリズムを利用して部品の平面パターン寸法を正確に計算し、曲げ加工や成形加工後の正確な最終形状を確保している。

伝統的な「ピンチ法」は、材料特性、曲げ半径、曲げ角度、金型構成、成形速度などの要素を組み込んだ経験的手法として、現在も広く用いられている。この方法は効果的ではあるが、オペレーターの経験に大きく依存し、矛盾が生じる可能性がある。

高度な計算ツールの出現により、コンピュータ支援設計（CAD）と有限要素解析（FEA）は、板金設計の精度と効率に革命をもたらしました。これらの技術により、スプリングバック、残留応力、ひずみ硬化などの複雑な現象を考慮した、成形プロセス中の材料挙動の精密なシミュレーションが可能になりました。

最新のCADシステムは、理論モデルと経験的データを統合した高度な曲げ補正アルゴリズムを採用しています。これらのアルゴリズムは、通常2つの主要なアプローチのいずれかを利用します：

1. 曲げ許容量法：この手法は、Kファクター（中立軸の位置）や材料特性などの要因を考慮し、曲げ部を通る中立軸の円弧長さを計算する。
2. 曲げ控除法：この方法は、フランジ長さの合計とフラットパターン長さの合計の差を求め、曲げ時の材料の変位を考慮する。

SolidWorks、Autodesk Inventor、Siemens NXなどの主要なCADプラットフォームは、カスタマイズ可能な曲げテーブルと材料ライブラリを備えた堅牢な板金設計モジュールを提供しています。これらのシステムでは、工場固有の曲げデータを統合できるため、デジタル設計と実際の製造プロセスとの整合性が確保されます。

さらに、機械学習や人工知能のような新しい技術は、曲げ計算を最適化するために適用されており、過去の生産データの膨大なデータセットを活用して予測を精緻化し、独自の材料と工具の組み合わせに適応させている。

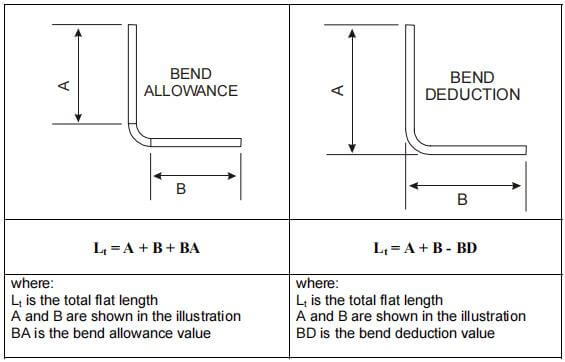
の基本概念の理解を深める。 板金デザイン を計算し、以下の点を要約して説明する：

• 2つの曲げアルゴリズムの定義： 曲げ代 と曲げ控除、そして実際の板金形状との関連性。
• との関係 ベンド控除 と曲げ代、そして曲げ控除アルゴリズムを使用しているユーザーが、どのように簡単にデータを曲げ代アルゴリズムに変換できるかについて説明します。
• Kファクターの定義、実用的な使用方法、異なる材料タイプに適用されるKファクター値の範囲。

2.曲げ代法

をより明確に理解するために 曲げ代図1は、板金部品の1つの曲げ部を示している。図2は、展開状態の部品を示している。

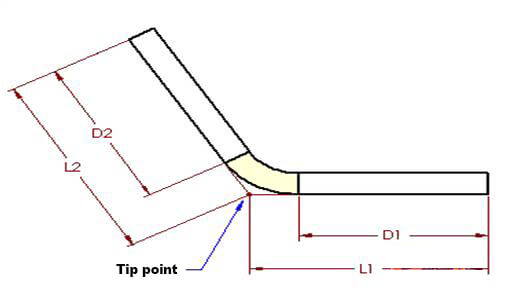
図1

図2

曲げ代アルゴリズムでは、シートメタル部品の展開長さ（LT）を、部品が平坦化された後の各セグメントの長さの合計と、平坦化された曲げ領域の長さとして記述します。

について 曲げ代 (BA)は平坦化された曲げ部分の長さを表す。したがって、部品の全長は式(1)で表すことができる：

lt = d1 + d2 + ba (1)

曲げエリア（図では薄い黄色で示されている）は、理論上、曲げ加工中に変形を受けるエリアである。

展開された部分の形状を決定するには、以下の手順に従う：

• 曲げ部分から曲げ部分を切り取る。
• 残りの2つの平らな部分を平らな面に置く。
• 長さの計算 平坦化された曲げ部分の
• 平らになった折り曲げ部分を2つの平らな部分でつなぎ合わせると、目的の折り曲げ部分ができる。

図ではBAで表されている、平らになった曲げ部分の長さを決める作業は、少し難しい。

BAの値は、材料の種類や厚さなどの要因によって異なる、 曲げ半径 と角度、曲げ工程、機械の種類、機械の速度。

BAの値は、板金材料メーカー、実験データ、経験、技術マニュアルなど、さまざまな情報源から得ることができる。

SolidWorksでは、BA値を直接入力するか、Kファクター（後述）を使用して値を計算することができます。

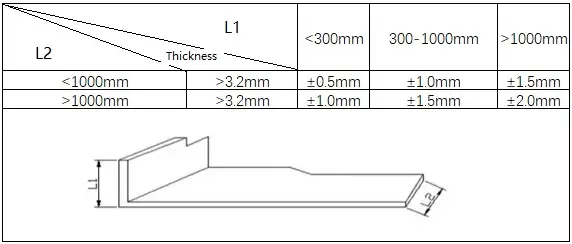
について ベンディングテーブル この方法は、厚さ、半径、角度が異なるさまざまな状況に対して、異なる曲げ許容値を指定する最も正確な方法である。

最初の曲げテーブルの作成には時間がかかるかもしれないが、一度形成してしまえば、その一部を将来再利用することができる。

各曲げ部分には、同じまたは異なる情報を入力することができます。

1) 一般的な曲げの基準

2) Z曲げの規格

3) V字曲げの規格

4) 基準 U曲げ

関連記事 V＆U字曲げ力計算機

3.曲げ控除法

ベンディング・デダクションとは、以下のようなプロセスにおける後退量を表す用語である。 板金曲げ.これもプロセスを記述するためのシンプルなアルゴリズムである。

図1と図2もこの概念に当てはまる。曲げ控除法によれば、部品の平坦化された長さ（LT）は、「先端点」（2つの平坦部の仮想的な交点）まで延びる2つの平坦部の長さの合計から曲げ控除（BD）を差し引いたものに等しい。

したがって、部品の全長は式（2）のように表すことができる：

lt = l1 + l2 - bd (2)

BDの値は、以下のような様々な情報源から決定または取得することができる。 金属材料 サプライヤー、実験データ、経験、方程式や表を含むエンジニアリング・マニュアルなど。

図3

4.曲げの関係 手当と曲げ控除

曲げ減点法に慣れているユーザーは、SolidWorksで一般的に採用されている曲げ許容量法との関係を理解することが重要です。

この2つの値の関係は、部品の曲げと展開の2つの形状を使えば簡単に推測できる。

式（1）と式（2）を比較すると、次のようになる：

lt = d1 + d2 + ba (1) lt = l1 + l2 - bd (2)

それゆえだ、

d1 + d2 + ba = l1 + l2 - bd (3)

図3において、角度Aは 曲げ角度この角度は、曲げ加工中に部品が振り回される角度と、曲げ領域によって形成される円弧の角度を表し、2つの半分で示される。

直角三角形の寸法と原理を使えば、以下の方程式を導くことができる：

d1 = l1 - (r + t)tan(a/2) (4) d2 = l2 - (r + t)tan(a/2) (5)

(4)式と(5)式を(3)式に代入することで、BAとBDの関係を求めることができる：

ba = 2(r + t)tan(a/2) - bd (6)

曲げ角度が90度の場合、この式は次のように単純化される：

ba = 2(r + t) - bd (7)

これらの式(6)と式(7)は、材料の厚さ、曲げ角度/半径などをパラメータとして使用するだけで、1つのアルゴリズムから他のアルゴリズムに変換する便利な方法を提供します。

SolidWorksユーザーにとって、これらの方程式は曲げ控除を曲げ許容値に変換する直接的な方法を提供します。

曲げ許容値は、部品全体または個々の曲げに使用することも、曲げデータテーブルに含めることもできます。

5.Kファクター法

Kファクターは、さまざまな幾何学的シナリオにおけるシートメタルの曲げと展開を説明する独立した値である。

また、異なる材料厚、曲げ角度、半径などの様々な条件下で曲げ許容範囲（BA）を計算するために使用される自律的な値でもある。

図4と図5は、Kファクターの詳細な定義を明確にするために用意されたものである。

図4

図5

板金部分の厚みに中立軸があることが確認できる。シート 金属材料 つまり、曲げ時に変形しない唯一の領域である。

図4と図5は、ピンクとブルーの領域の境界を示している。

曲げ加工中、ピンク色の領域は圧縮され、青色の領域は伸びる。中立のシートメタル層が変形していない場合、曲げ領域における円弧の長さは、部品が曲げられようが平らにされようが変わりません。

その結果、曲げ代（BA）は、板金部品の曲げ領域における中立層の円弧の長さに等しくなるはずであり、これは図4に緑色で示されている。

シートメタルの中立層の位置は、延性など特定の材料の特性に左右される。

中立の板金層と表面との間の距離を "t"、すなわち板金部品の表面から材料への厚さ方向の深さと仮定する。

その結果、中立層の円弧の半径は（R＋t）で表すことができる。この式と曲げ角度を用いて、中立層の円弧の長さ（BA）を計算することができる。

BA = Pi(R+T)A/180

シートメタル中性層の定義を簡素化し、すべての素材に適用できるようにするため、Kファクターという概念が導入された。

Kファクターの定義は、シートメタルの中性層の厚さとシートメタル部品の素材全体の厚さの比である。言い換えれば、Kファクターは次のように定義される：

K = t/T

Kファクターが0.25の場合、中性層は板金材料の全厚みの25%に位置することを示す。

同様に、これが0.5であれば、中性層が厚さ全体の50%にあることを意味する。

上記の式を組み合わせると、以下の式（8）が得られる：

BA = Pi(R+K*T)A/180 (8)

したがって、Kの値は常に0と1の間になる。

Kファクターが0.25の場合、中性層が板金材料の厚さの25%に位置することを意味する。

同様に0.5であれば、中性層は全体の厚みの50%に位置することを意味する。

Kファクターの起源は、板金材料のサプライヤー、テストデータ、経験、マニュアルなどの伝統的な情報源にまで遡ることができる。

しかし、提供された値が明確なKファクターとして表現されない場合もあるが、それでも両者の関係を見出すことは可能である。

例えば、マニュアルや文献に中立軸が「シートメタル表面から0.445倍の材料厚さに位置する」と記載されている場合、Kファクターが0.445、つまりk=0.445と解釈することができる。

このKの値を式（8）に代入すると、以下の式が得られる。

ba = a (0.01745r + 0.00778t)

式（8）を別の方法で修正し、式（8）の定数を計算し、すべての変数を保持すると、以下のようになる：

ba = a (0.01745 r + 0.01745 k*t)

2つの方程式を比較すれば、0.01745 * k = 0.00778となり、kは0.445と計算できる。

SolidWorksシステムには、曲げ角度が90度の場合の特定の材料に対する曲げ代アルゴリズムも用意されていることが判明しました。各材料の計算式は以下の通りです：

• 軟質黄銅または軟質銅：ba = (0.55 * t) + (1.57 * r)
• 準硬質銅、または黄銅、軟鋼、アルミニウムなどの素材： BA = (0.64 * T) + (1.57 * R)
• 青銅、硬質銅、冷間圧延鋼、バネ鋼：BA = (0.71 * T) + (1.57 * R)

実際、式（7）を単純化し、曲げ角度を90度に設定することで、定数を計算することができ、式は以下のように変形できる：

BA = (1.57 * K * T) + (1.57 * R)

従って、上記の計算式を比較すると、軟質黄銅または軟質銅材料のKの値は、1.57xk=0.55、またはK=0.35と求めることができる。

同じ方法で、上記の数種類の材料のKファクター値を計算するのは簡単である。

• 軟質黄銅または軟質銅：K = 0.35
• 半硬質銅、または真鍮、軟鋼、アルミニウムなどの素材：K = 0.41
• 青銅、硬質銅、冷間圧延鋼、バネ鋼：K = 0.45

前述したように、Kファクターの値を得るための情報源は、材料メーカー、試験データ、経験、マニュアルなどいくつかある。

Kファクター法を使用して正確なシートメタルモデルを確立するには、エンジニアリング要件を満たすKファクターの適切なソースを見つけることが重要です。こうすることで、物理的な部品の結果が希望通りの精度になることが保証されます。

状況によっては、単一のKファクター値だけでは正確な結果を得ることができない場合があります。特に、幅広い曲げシナリオに対応する必要がある場合です。

このような場合は、部品全体の1回の曲げに対して曲げ代（BA）の値を直接使用するか、曲げテーブルを使用して、全範囲にわたって異なるA、R、T値に対応する異なるBA、曲げ控除（BD）、またはKファクターの値を記述することをお勧めします。

さらに、方程式を使用して、SolidWorksが提供するサンプル曲げ表のようなデータを生成することもできます。必要に応じて、ベンドテーブルのセルを実験的または経験的データに基づいて変更することもできます。

SolidWorksのインストールディレクトリには、曲げ代テーブル、曲げ控除テーブル、Kファクターテーブルが含まれており、必要に応じて編集やカスタマイズを行うことができます。

• 板金曲げ計算機

6.概要

この記事では、板金部品の設計と製造に使用される一般的な計算方法とその基礎となる原理について、包括的な概要を説明します。

本書では、曲げ許容範囲、曲げ控除、Kファクターの計算を取り上げ、これらの方法の違いと相互関係を説明している。

業界のエンジニアや技術者にとって有益な参考資料となる。

注：

• Tanは接三角関数の簡略化された表現である。
• PIは定数π（3.14159265...）を表す。