スプリング101：性能と用途を考慮した13のタイプを探る
機械工学におけるスプリングの多用途性に驚嘆したことはありますか？自動車のサスペンションから精密機器に至るまで、この縁の下の力持ちは重要な役割を果たしています。このブログ記事で、私たちは...
橋が突然激しく揺れ始めたり、歌手が高音を出すとワイングラスが割れたりするのはなぜか、不思議に思ったことはないだろうか。このブログでは、固有振動数と共振周波数という魅力的な概念を探求し、それらが工学的な驚異から日用品に至るまで、あらゆるものにどのような影響を与えているかを明らかにします。これらの振動に隠された秘密を解き明かし、それらがどのように私たちの世界を形作っているのかを学ぶことを期待しています。
日常的な分析では、固有振動数と共振周波数を混同し、同じものだと考えてしまうことが多い。
実際、これは厳密ではない。
固有振動数は構造物の固有特性の性能であり、共振振動数は外力に対する構造物の応答性能である。
1自由度システムとは、位置が任意の時点で1つの一般化された座標によってのみ完全に決定できるシステムのことである。もっと簡単に言えば、物体に作用する力は一方向だけである。下図の人形の運動は、バネ-質量系として表すことができる。
バネ・マス・システムの簡略化したモデルを下図に示す。
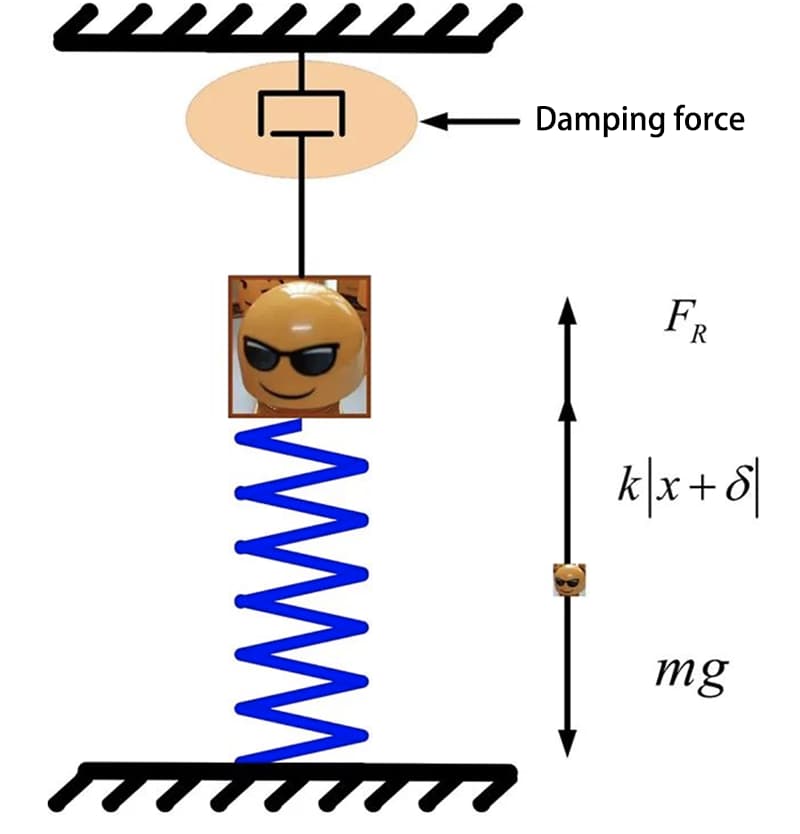
ピックアップブロックの静止バランス位置を座標原点とし、バネの変形方向に沿って鉛直下方に移動したときを正とする。ブロックとバランス位置との距離をxとすると、ブロックの微分運動方程式は次のように表すことができる：
ここで、mはブロックの質量、kはバネ剛性、cは粘性係数、2n=c/mは減衰減衰係数であり、減衰係数がゼロの場合は非減衰振動系に相当する。
固有振動数 Pn：
固有振動数は質量と剛性にのみ依存し、減衰などの要因には影響されない。構造上の境界接続、 材料特性しかし、これらの影響は剛性と質量に反映され、最終的な決定要因ではない。
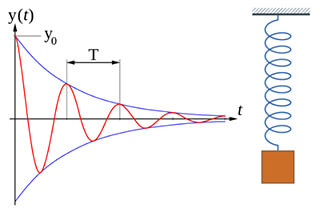
自由振動とは、外部からの加振を伴わない系の振動のことで、運動軌跡は初期状態や自然特性に関係する。
強制振動とは、外部からの加振を受けてシステムが発生させる振動を指す。
外部加振は一般に、時間の周期的または非周期的な関数であり、中でも単純調和加振が最も単純である。
単純調和励起力をこうする：
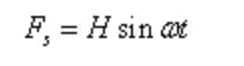
ここで、Hは加振力の振幅、ωは加振力の角周波数である。
ブロックが平衡位置からxだけずれると、ブロックの微分運動方程式は次のようになる。
ここで、h=H/m、上式は粘性減衰を伴う1自由度の強制振動の微分方程式であり、2次の定係数線形非均質常微分方程式である。
上式は、回路理論で学んだ容量性負荷電圧応答式と完全に一致しており、これは2次の定係数線形非同次常微分方程式である。
抵抗はエネルギーを消費するだけで、蓄えることはないからだ。
単純な調和加振の下では、減衰系の微分運動方程式の全解は次のように設定される：
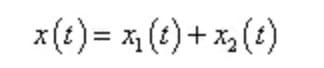
ここで、x1 (t)は均一解であり、自由減衰振動である；
減衰が存在するため、減衰した振動部分はある一定の時間が経過すると消滅する。
その解法は自由振動の場合と同じなので、ここでは繰り返さない。
ここでは、特別な解x2 (t)は強制振動によって発生し、次式で表される：
そのうちのひとつだ、
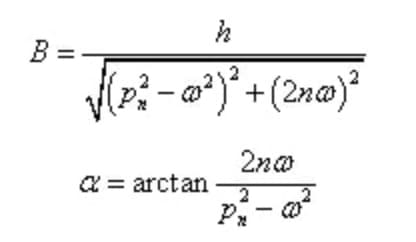
定常強制振動の振幅と位相遅れは、初期条件には依存せず、システムの特性と加振にのみ依存する。
周波数比、減衰比、振幅増幅率を設定する：
上記の式は次のように書き換えることができる：
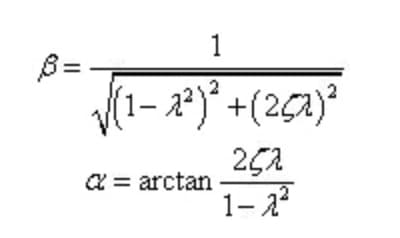
これに基づいて、強制振動下でのシステムの応答を知ることができる。
よりよく理解するために、異なる減衰比、周波数比、振幅増幅係数の関係を図示することができる。周波数は、低周波、中周波、高周波の3つの領域に分けられている。図からわかるように、低周波領域、高周波領域ともに、ダンピングが振幅増幅係数に与える影響は小さい。従って、減衰系は非減衰系として単純化でき、計算が容易になります。
固有振動数とは、システムの構造特性に固有の特性であり、減衰などの外的要因とは無関係に、質量と剛性のみによって決定される。n自由度システムでは、n個の異なる固有振動数が存在し、連続システムでは無限の固有振動数が存在する。
共振は、外部からの加振周波数がシステムの固有周波数と密接に一致するか、または一致する場合に発生し、構造体が著しく増加した振幅で振動する。この現象は、添付図の青い円で表されている。共振周波数は、減衰の少ないシステムでは固有振動数に近似していることが多いが、減衰の多い構造では固有振動数からずれることがあり、通常は固有振動数よりも低くなる。
システム設計では、特定の共振ピーク周波数だけでなく、図中の中間周波数領域に相当する周辺の共振帯域も避けることが極めて重要である。この帯域内ではシステムの応答がかなり増幅されたままとなるため、このような予防措置が必要となる。エンジニアは、システムの通常動作や近隣の機器からの外部加振が、この重要な範囲に入らないようにしなければなりません。
共振は、有益なものにも有害なものにも、重大な影響を及ぼす可能性がある。悪い影響としては、リフティングビームの崩壊、ヘリコプターの地上共振、機械の損傷、低周波による構造物の故障などが考えられる。逆に、楽器では共鳴を意図的に利用して、望ましい音色や倍音を作り出している。
共振に伴うリスクを軽減するために、設計者はさまざまな戦略を採用している：
共振を理解し管理することは、土木工学や航空宇宙から精密製造や楽器設計に至るまで、幅広い分野で不可欠です。有限要素解析や実験モード解析などの高度な解析ツールは、複雑なシステムの共振挙動を予測し、特徴付ける上で重要な役割を果たします。
MachineMFGの創設者として、私は10年以上のキャリアを金属加工業界に捧げてきました。豊富な経験により、板金加工、機械加工、機械工学、金属用工作機械の分野の専門家になることができました。私は常にこれらのテーマについて考え、読み、執筆し、常にこの分野の最前線にいようと努力しています。私の知識と専門知識をあなたのビジネスの財産にしてください。
JA 
EN 
AR 
DE 
ES 
FR 
IT 
NL 
PT 
PT_BR 
RU 
KO