強さと硬さ：主な違いを理解する
同じ荷重をかけても、ある材料は曲がり、別の材料は壊れるのはなぜか。その違いは強度と剛性にある。この記事では、これらの重要な特性について説明し、強度を...
ある材料は簡単に曲がるのに、ある材料は硬いままなのはなぜだろうと不思議に思ったことはありませんか？このブログでは、弾性率と剛性の魅力的な世界に飛び込み、工学におけるその重要な役割を解き明かします。最後には、これらの特性が日常的な材料の強度と柔軟性にどのような影響を与えるかを理解できることでしょう。
弾性係数：材料の弾性変形段階における法線応力とそれに対応する法線ひずみの比。
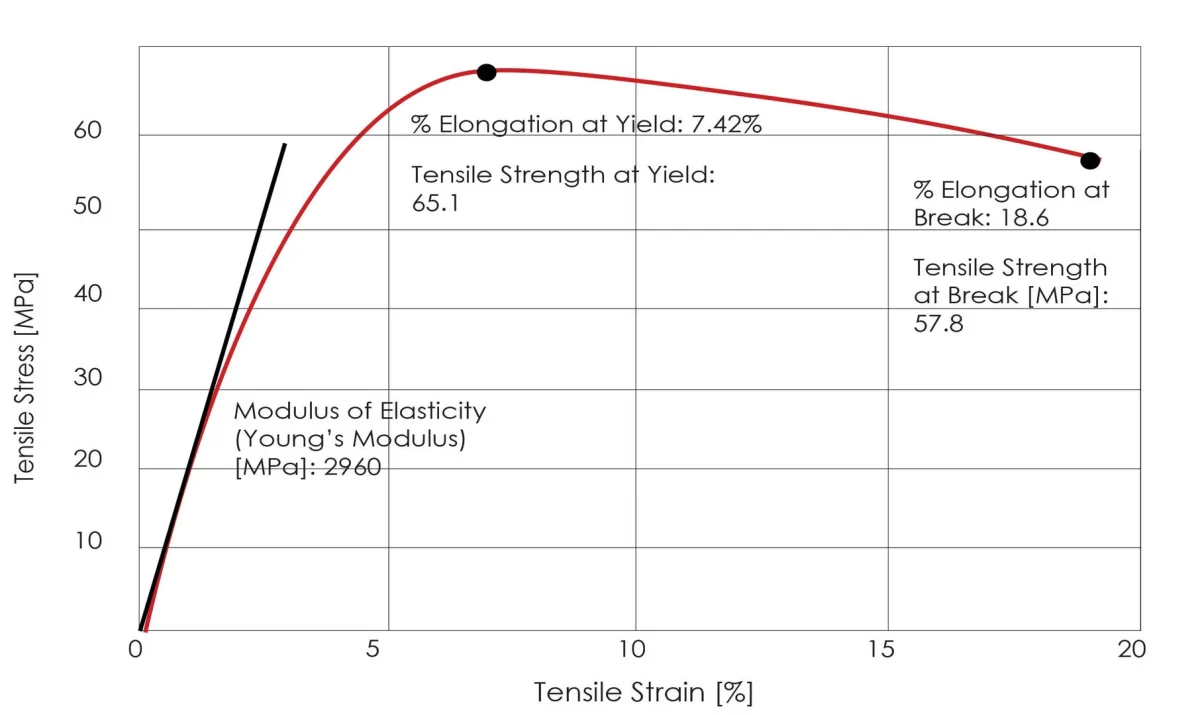
弾性変形の段階では、フックの法則に従い、材料の応力とひずみは比例し、その比例係数は弾性係数と呼ばれる。
弾性率」という用語は、材料の弾性の一般的な説明である。ヤング率、せん断弾性率、体積弾性率など、いくつかの特定の弾性率が含まれる。
したがって、「弾性率」と「体積弾性率」は包括的な用語である。
エラストマーに外力（「応力」と呼ばれる）が加わると、その形状は変化する（「ひずみ」と呼ばれる）。弾性率は、応力とひずみの比として定義されます。
例えば、こうだ：
線形ひずみ：
細い棒に引張力Fを加えた場合、線応力は引張力を棒の断面積Sで割ったものとして計算される。
線形ひずみは、ロッドの伸び（dL）を元の長さ（L）で割った値として計算されます。
線形応力を線形ひずみで割ったものがヤング率で、E = (F / S) / (dL / L)となる。
せん断ひずみ：
エラストマーに横方向の力（通常は摩擦力）fが加わると、エラストマーは四角形から菱形に変化する。
この変形角は "せん断ひずみ "と呼ばれ、対応する力を応力面積で割ったものが "せん断応力 "と呼ばれる。
せん断応力をせん断ひずみで割った値は、せん断弾性率G＝（f／S）／aに等しい。
体積のひずみ：
エラストマーに全体的な圧力Pがかかると、"体積応力 "と呼ばれる。
エラストマーの体積減少（-dV）を元の体積（V）で割ったものを "体積ひずみ "と呼ぶ。
体積応力を体積ひずみで割った値は、体積弾性率 K = P / (-dV / V)に等しい。
一般に、混同がない場合、金属材料の弾性率はヤング率を指し、正の弾性率としても知られている。
単位：E（弾性率）の単位はGPa。
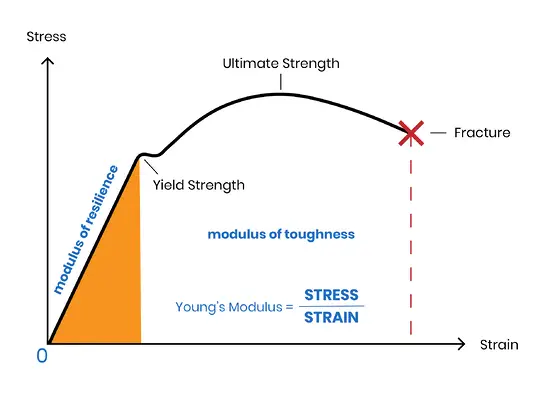
弾性率は工学材料の重要な性能パラメータである。
マクロな視点からは、物体の弾性変形に対する抵抗力を測定し、ミクロな視点からは、原子、イオン、分子間の結合力を反映する。
結合強度に影響を与える要因は、結合様式、結晶構造、化学組成、微細構造、温度など、材料の弾性率にも影響を与える可能性がある。
のヤング率である。 金属材料 は、合金組成、熱処理状態、冷間塑性変形が異なるため、5%以上変動する可能性がある。
しかし、一般的には、弾性率 金属材料 は機械的特性の指標であり、構造には影響されない。
合金化、熱処理（繊維組織）、冷間塑性変形が弾性率に及ぼす影響は限定的で、温度や負荷率などの外的要因は無視できるほど小さい。
したがって、一般的な工学用途では、弾性率は一定とみなされる。
単位：弾性率はGPa（ギガパスカル）。
弾性率は、材料の弾性変形に対する抵抗力を示す尺度である。
この値が大きいほど、ある量の弾性変形を生じさせるのに必要な応力が大きくなり、材料が硬くなり、与えられた応力下での弾性変形が小さくなることを意味する。
Eで表される弾性率は、材料が外力を受けて単位弾性変形を起こすのに必要な応力の大きさを示す尺度である。
これは、弾性変形に抵抗する材料の能力を表し、次のような剛性と比較することができる。 春.
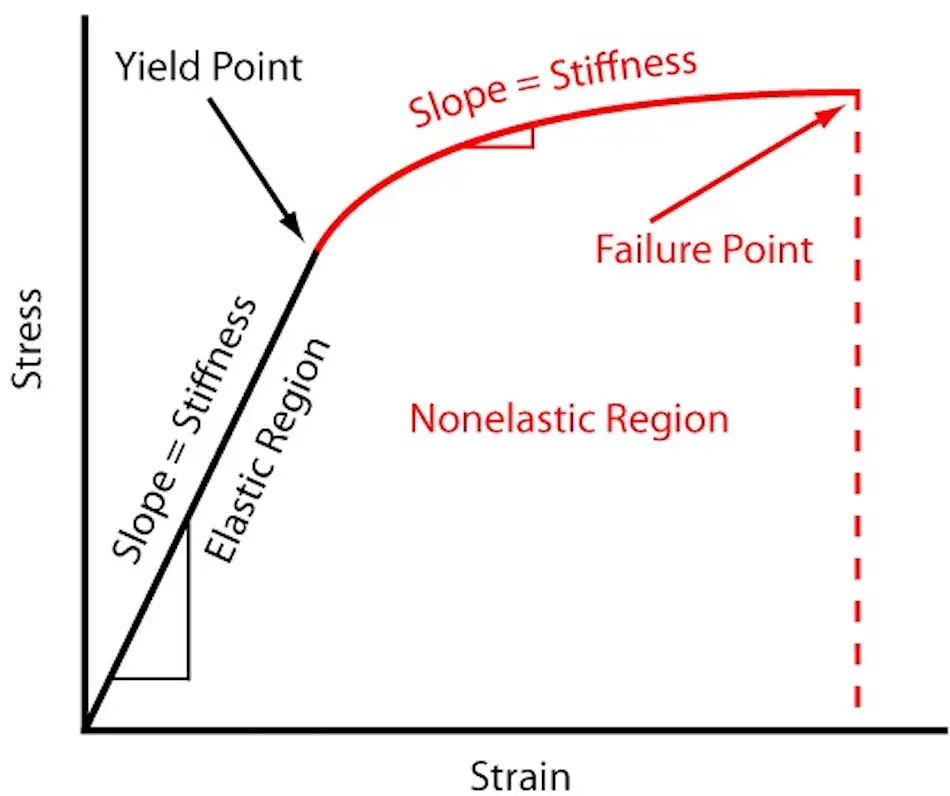
剛性」とは、構造物や部品が弾性変形に抵抗する能力のこと。単位ひずみを発生させるのに必要な力またはモーメントによって決定される。
回転剛性に関しては「k」で表され、「k＝M／θ」で計算することができる。ここで「M」は印加トルク、「θ」は回転角度である。
その他の硬さは以下の通り：
剛性の計算方法は、小変位理論と大変位理論の2つのアプローチに分けられる。
大変位理論は、応力後の構造物の変形を考慮し、それに応じて平衡方程式を形成するため、正確な結果が得られるが、計算過程が複雑になる。
これに対して小変位理論は、構造物が大きく変形しないことを前提としているため、外力から内力を求め、それを用いて変形を計算することができる。
このアプローチは、解くのがはるかに簡単であるため、ほとんどの機械設計アプリケーションで広く使用されている。
例えば、梁の曲げ変形の計算では、実際の変形が非常に小さいため、しばしば小変位理論が採用される。
この理論では、曲率式のたわみの一次導関数を無視し、たわみの二次導関数を用いて梁軸の曲率を近似することで、微分方程式を線形化し、解法を単純化します。
複数の荷重が同時に作用する場合、それぞれの荷重による曲げ変形を個別に計算し、それを組み合わせることができる。
静的荷重下での変形に対する抵抗は静的剛性と呼ばれ、動的荷重下での変形に対する抵抗は動的剛性と呼ばれ、単位振幅に必要な動的力の量を意味する。
干渉する力がゆっくりと変化する場合（すなわち、干渉する力の周波数が 固有振動数 構造体の）、動的剛性は本質的に静的剛性と等しい。
しかし、干渉力が急激に変化する場合（すなわち、干渉力の周波数が構造物の固有周波数よりはるかに大きい場合）、構造物の変形は比較的小さくなり、したがって動的剛性も比較的大きくなる。
干渉力の周波数が構造物の固有振動数に近い場合、共振が起こり、動的剛性が最小となり、構造物が最も変形しやすくなり、その動的変形は静的荷重による変形の数倍から10倍以上に達することもある。
部品の過度の変形は、その動作に影響を及ぼす可能性がある。
例えば、ギヤシャフトの過度の変形はギヤのかみ合わせに影響を与え、工作機械の過度の変形は加工精度を低下させる。
剛性に影響を与える要因には、材料の弾性率と構造形式がある。構造形式を変えると、剛性に大きな影響を与えることがあります。
剛性計算は振動理論と構造安定性解析の基礎である。質量が一定の場合、剛性が高いと固有振動数が高くなります。
静的不定構造における応力分布は、各部の剛性比に関係する。
で 破壊力学 解析では、ひび割れた部材の応力拡大係数をその柔軟性に基づいて決定することができる。
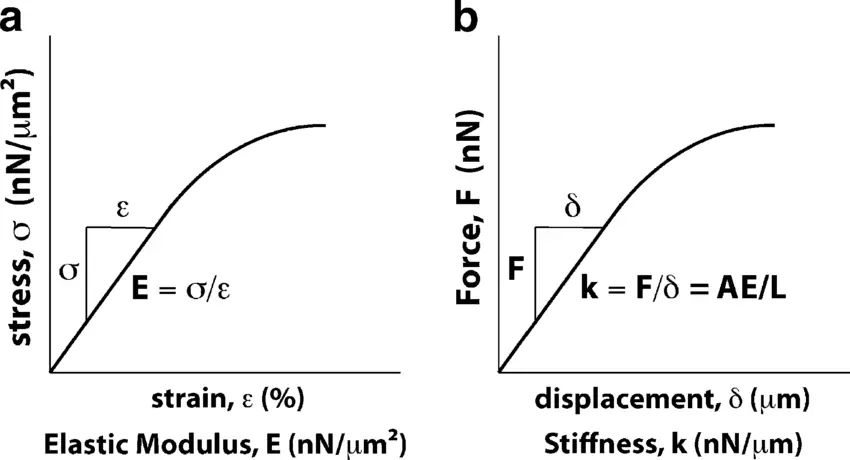
剛性と弾性率は材料科学における基本的な概念であり、それぞれ材料の変形に対する抵抗力の異なる側面を表しています。両者は関連していますが、材料の解析や応用においてはそれぞれ異なる役割を果たします。
ヤング率とも呼ばれる弾性率は、応力下での変形に抵抗する材料固有の能力を示す尺度です。材料の応力-ひずみ曲線の線形弾性領域における応力（単位面積当たりの力）とひずみ（比例した変形）の関係を数値化したものです。弾性率は材料の特性であり、材料の形状や大きさとは無関係です。弾性率は、パスカル（Pa）のような圧力の単位で表されます。
一方、剛性とは、より広い意味での用語であり、荷重が加わった際の構造体の弾性変形に対する抵抗力を指す。剛性は材料特性だけでなく、構造物の形状や境界条件にも依存します。剛性は通常、単位変位を達成するのに必要な力（ニュートン毎メートル、N/mなど）で表される。
構造要素の剛性は、材料の弾性係数と要素の形状から求めることができます。例えば、梁の曲げ剛性（EI）は、弾性係数（E）と梁断面の慣性モーメント（I）の積です。同様に、ねじり剛性（GI）は、せん断弾性率（G）と極慣性モーメント（I）の積です。
特に、スピンドル、ガイドレール、リードスクリューなど、荷重がかかっても形状を維持しなければならない部品では、剛性は工学設計において極めて重要です。また、航空機の翼や高精度の組立部品のように、厳密な変形制御を必要とする構造物にも不可欠です。
強度とは、材料が外力による永久変形や破壊に抵抗する能力のことである。降伏強さ、引張強さ、圧縮強さ、曲げ強さなど、さまざまな種類の強さが含まれる。これらの特性は、機械部品の耐荷重性と耐久性を決定する上で非常に重要である。
剛性と弾性率の違いを理解することは、機械部品や構造物の設計および解析に不可欠です。弾性率が材料の変形に対する本質的な抵抗力を示すのに対し、剛性は材料特性と幾何学的要因の両方を考慮し、構造物の変形に対する全体的な抵抗力を表します。どちらの概念も、工学設計の性能と信頼性を確保するために不可欠です。
MachineMFGの創設者として、私は10年以上のキャリアを金属加工業界に捧げてきました。豊富な経験により、板金加工、機械加工、機械工学、金属用工作機械の分野の専門家になることができました。私は常にこれらのテーマについて考え、読み、執筆し、常にこの分野の最前線にいようと努力しています。私の知識と専門知識をあなたのビジネスの財産にしてください。
JA 
EN 
AR 
DE 
ES 
FR 
IT 
NL 
PT 
PT_BR 
RU 
KO