リベット接続の計算を知る：エキスパートガイド

リベット接続

リベット接合は、2つ以上の材料、特に金属を接合する基本的な方法であり、様々なエンジニアリングや建設用途で広く使用されている。リベットは永久的な機械的ファスナーであり、一端に頭部がある滑らかな円筒形のシャフトから成る。取り付け工程では、あらかじめ開けられた穴にリベットを挿入し、尾端を変形させて2つ目の頭部を作り、それによって材料同士を固定します。

歴史的な例

歴史的に、リベット接合は重要な構造物の建設に不可欠であった。顕著な例としては、パリのエッフェル塔やサンフランシスコのゴールデン・ゲート・ブリッジがある。これらの構造物は、時の試練に耐え、信頼できる性能を発揮し続けるリベット接合部の耐久性と強度を示している。

リベットのパターン

チェーン、ジグザグ、または千鳥のようなパターンでのリベットの配置は、接合部の性能に影響する。

• チェーンパターン： リベットは接合部に沿って一直線に配置される。このパターンは実施しやすいが、他のパターンに比べて荷重を均等に分散できないことがある。
• ジグザグ模様： リベットはジグザグに配置される。このパターンは荷重を均等に分散させ、接合部の強度を向上させます。
• 千鳥パターン： ジグザグ・パターンと同様に、スタッガー・リベットは強化された荷重分散を提供し、応力集中のリスクを低減する。

素材の選択

リベットは、アルミニウム、鋼、真鍮、銅など、さまざまな材料で作ることができる。材料の選択は、強度、耐食性、延性などの特定の要件によって異なります。

メリットとデメリット

メリット

• 負荷分散： リベット接続は荷重を均等に分散し、材料の破損につながる応力集中のリスクを低減します。
• 耐久性がある： リベット接合は長持ちする耐久性で知られ、重要な構造物に適している。
• 汎用性がある： リベットは異種材料を接合することができ、動的荷重の下で優れた性能を発揮する。

デメリット

• 設置の複雑さ： リベッティングは、溶接やボルト締めに比べて手間がかかる。
• パーマネント・ネイチャー 一度取り付けたリベットを取り外すのは難しく、分解は困難を極める。

溶接やボルト締めとの比較

溶接

• 利点がある： 溶接は連続した接合部を作り、特定の用途ではより速くできる。
• デメリット 溶接には熟練した技術が必要であり、熱応力が加わって材料が歪む可能性がある。

ボルト締め

• 利点がある： ボルト接続は、分解や調整が容易である。
• デメリット ボルトは応力集中を引き起こす可能性があり、締め付けを確実にするために定期的なメンテナンスが必要になる場合があります。

リベット・ジョイントの望ましいシナリオ

リベット接合は、接合部が動的荷重に耐える必要がある場合や、異種材料の接合が必要な場合に好まれる。また、歴史的な意義や重要な構造物における実証済みの信頼性からも選ばれています。

リベット接続の主な種類

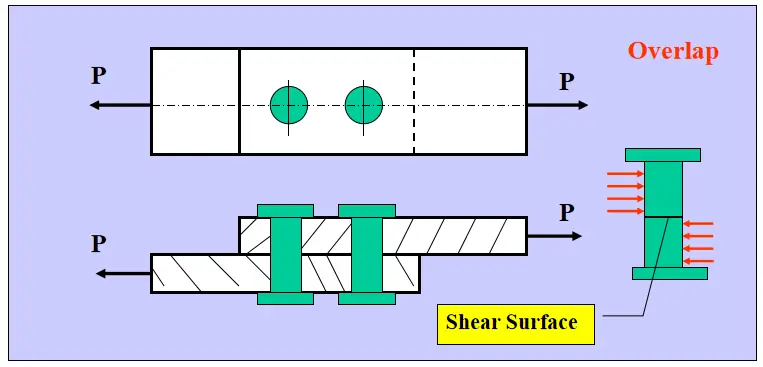
シングルカバー・バットジョイント

ダブルカバー・バットジョイント

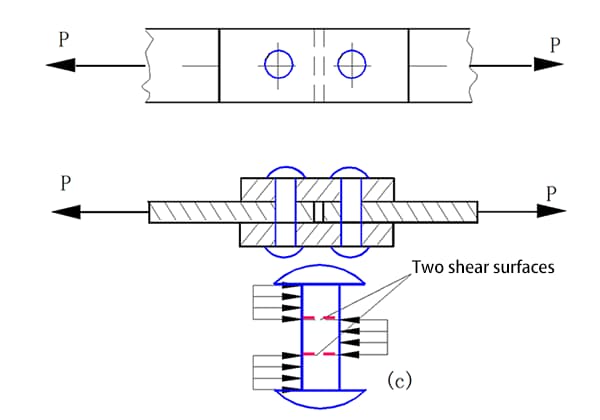
リベットグループの横荷重耐性

上図のような）リベット接合では、計算を簡単にするため、次のように仮定する：

• リベットの方法に関係なく、曲げ効果は考慮されない。
• 外力の作用線がリベット群の断面の重心を通り、同じ群の各リベットの直径が同じであれば、各リベットに作用する力も等しい。

各リベットに作用する力の計算式は次のとおりである：

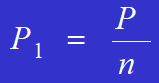
例

枚の鋼板を4個のリベットで接合する。鋼板とリベットの材質は同じである。リベットの直径はd=16mmである。 鋼板 はb=100mm、t=10mm、P=90KN、リベットの許容応力は[τ]=120MPa、許容降伏応力は[σ_ジェー]=120MPa、鋼板の許容引張応力は[σ]=160MPaである。リベット接合部の強度を計算し、確認しなさい。

(1) リベットのせん断強度：

各リベットに作用する力はP/4である。

各リベットに作用するせん断力は次式で与えられる：

(2) リベットの破砕強度：

破砕によって各リベットに作用する力は次のとおりである：

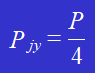
押しつぶされるリベットの面積は次のとおりである：

(3) 鋼板の引張強さ

考える質問だ：

ダウエルピンAのせん断面の面積。
ダボピンAjyの押し出し面の面積。

追加の質問だ：

に図のような形の穴を開ける。 厚さ5mm 鋼板。鋼板材料のせん断強度の限界を𝜏とすると_𝑏 = に必要な打ち抜き力Fを計算する。 パンチプレス.

解答せん断面の面積は

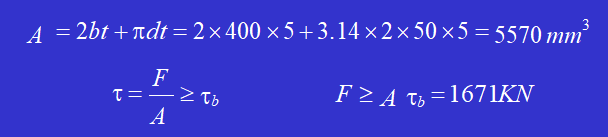
追加の質問だ：

の最大パンチ力 パンチプレス の許容圧縮応力[]は、P = 400KNである。 パンチ材料 は440MPaであり、鋼板のせん断強度の限界は𝜏 = 360MPaである。パンチが打ち抜くことのできる最小直径dと、打ち抜くことのできる鋼板の最大厚さ𝜹を決定しなさい。

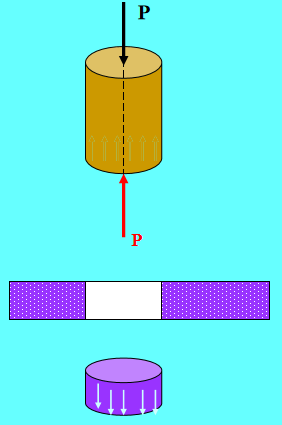
解答パンチは軸方向に圧縮変形する。

鋼板のせん断破壊条件による：

例

2本の鋼鉄製レールを複合梁にリベットで打ち込む場合、接続状況は図aとbのようになる。

各鋼製レールAの断面積は8000mm、各鋼製レールの断面積の自重に対する慣性モーメントはI＝1600×10mmである。リベット間隔sは150mm、直径d＝20mm、許容せん断応力［τ］は95MPaである。梁の内部せん断力Qが50kNである場合、リベットのせん断強度を検証しなさい。上下の鋼製レール間の摩擦は考慮しない。

解決方法上下2本の鋼鉄レールが全体として曲がるとき、上側の鋼鉄レールの断面積には圧縮応力がかかり、下側の鋼鉄レールの断面積には引張応力がかかる。

隣接する断面の曲げモーメントが異なるため、対応する点の法線応力が異なり、そのため上下の鋼製レールの接触面に沿って長手方向に変位する傾向があり、リベットがせん断力を負担する原因となる。

リベットの各列が負担する剪断力は、長手方向距離Sで鋼鉄レールの2つの断面にかかる圧縮（引張）力の差に等しい。

スチールレールが接触面のあらゆる場所でせん断応力を伝えると仮定すると、接触面の幅はbとなる。

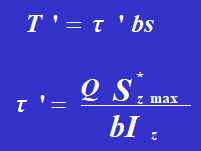
S_{ゼットマックス} スチールレールの断面積の中立軸に対する静モーメントを表す。

I_z は中立軸に対する断面全体の慣性モーメント。

リベットのせん断応力は次のとおりである：

リベットのせん断応力は強度基準を満たす。

ねじり荷重を受けるリベット・アセンブリ

ねじり荷重を受けるリベット・アセンブリ（図参照）。

リベット・アセンブリの断面の重心を0点とする。

鋼板上の任意の直線（OAまたはOBなど）が回転後も直線であると仮定すると、各リベットの平均せん断ひずみは、リベット断面の中心から点Oまでの距離に比例する。

各リベットの直径が同じであれば、各リベットにかかる力は、リベット断面の中心からリベット組立断面の中心Oまでの距離に比例し、その方向は点と中心Oを結ぶ線に垂直である。

P_i は各リベットに作用する力を表し、a_i は、与えられたリベットの断面の中心からリベット組立体の断面の重心までの距離を表し、Oと表記される。

偏心横荷重を受けるリベット組立体（図a参照）。

リベット・アセンブリに作用する偏心荷重Pを重心点Oに単純化すると、重心点Oを通過する力Pとモーメントが得られる。 m = Pe 点Oを中心に回転する。

同じリベット組立体の各リベットの直径が同じであれば、横力Pによって引き起こされる力P1′とモーメントmによって引き起こされる力P1 "を計算することができる。各リベットに作用する力はP1′とP1 "のベクトル和である。各リベットにかかる力P1を決定した後、最大力を持つリベットのせん断強度と圧縮強度を別々にチェックすることができる。

例

外力 P は 12 kN であることが知られている。リベットの直径は 20 mm であり、各リベットは単一せん断を受ける。最大力の下でのリベット断面の最大せん断応力を計算しなさい。

解決策

リベット組立体はx軸に関して対称であり、回転中心はリベット2とリベット5を結ぶ線とx軸との交点である点Oにある。

1.点Oへの力Pを単純化すると、次のようになる：

P = 12 kN。

m=12 0.12=1.44KN.m

2.回転中心を通る力Pの作用の下で、各リベットが同じ直径と材質であることを考慮すると、各リベットにかかる力は等しい。

3.モーメントmの作用の下で、各リベットが負担する力は、リベットから回転中心までの距離に比例する。

バランス方程式によれば

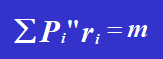
方程式を解くとこうなる：

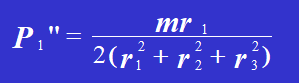
だから

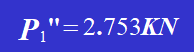
4.各リベットの力図を描き、ベクトル Pi'と Pi "を組み合わせて、各リベットに作用するせん断力の合計を、その大きさと方向を含めて求めなさい。リベット 1 とリベット 6 が最大力を負担し、最大力の値は次のとおりであると結論づけられる：

リベット断面のせん断応力は次のとおりである：

よくある質問

以下は、よくある質問に対する回答である：

建築に使われるリベットにはどのような種類がありますか？

建築では、様々なタイプのリベットがそのユニークな特性と用途のために利用される。丸リベットとしても知られるソリッド・リベットは、最も一般的で最も古いタイプで、ソリッド軸と頭部で構成される。それらはハンマーまたは圧着工具を使用して尾部を変形させることによって取り付けられ、その高い強度と信頼性のために広く使用されている。構造用スチール・リベットはソリッド・リベットに似ているが、橋や高層ビルなどの商業建築における高応力用途のために設計されている。

ブラインド・リベット、またはポップ・リベットは、その中心を通るマンドレルを持つ管状のリベットで、リベッターを使って取り付けられます。それらは、接合部の裏側へのアクセスが制限されている用途に理想的です。ドライブ・リベットは、ブラインド・リベットと同様に、取り付けに特別な工具を必要とせず、ハンマーで所定の位置に打ち込まれ、穴がパネルやブロック全体を貫通しない用途に適しています。

フラッシュ・リベット、または皿リベットは、皿頭と穴を持ち、表面と同一平面に位置することを可能にし、空気抵抗を減らし、滑らかな表面仕上げを提供する。スプリット・リベット(分岐リベット)は、材料に打ち込まれたときに反対方向に分岐する鋭い端を特徴とし、木材、プラスチック、革のような柔らかい材料の接合に理想的です。管状リベットは、一方の端に頭部、他方の端に尾部を持つ中空であり、取り付けにあまり力を必要とせず、固定される材料が柔らかい用途で使用される。

リベットは、ステンレス鋼、鋼、アルミニウム、真鍮、銅を含む様々な材料から作られ、それぞれがプロジェクトの特定の要求に基づいて選択される。これらの材料は異なる強度、耐食性、重量特性を提供し、リベットを様々な建設用途に多用途にします。

リベット接合と溶接接合との比較は？

リベット継手と溶接継手を比較するとき、いくつかの重要な相違点と考慮事項が現れる。溶接継手は一般に、リベット継手と比較してより高い強度と耐荷重性を提供する。健全な溶接継手は母材の強度の100%を達成することができるが、リベット継手はリベットのために開けられた穴による断面積の減少のために強度が低い。

設計と設置の面では、溶接の方が、あらかじめ穴を開けたり、リベットのような部品を追加したりする必要がないため、より単純で迅速であることが多い。しかし、リベッティングは穴あけ、締め付け、リベットの平坦化を必要とするため、より時間と労力がかかる。

振動と疲労の下での性能は2つの方法で異なる。リベット接合は、リベットの変形と膨張が時間の経過とともに接合部を強化することができるため、繰り返し荷重と振動に耐えるのに優れている。溶接継手は、強いが、繰り返される負荷サイクルの下では劣化の影響を受けやすい。

材料と適合性に関して言えば、融点を考慮する必要がないため、異種材料の接合にはリベッティングの方が汎用性が高い。しかし溶接は、融点と熱特性が適合する材料を必要とする。

美観上、溶接継手は、後加工後に滑らかな表面仕上げを提供することができ、これは、リベット継手の目に見えるリベット頭部と比較して、しばしばより好ましい。

メンテナンスと分解に関しては、リベット・ジョイントは、リベットをドリルで開けて交換できるため、分解と修理が容易である。溶接継手はより永久的であり、分解には切断と再溶接が必要で、時間とコストがかかる。

重量と構造の完全性という点では、溶接構造はリベットやストラップのような追加材料を必要としないため、一般的に軽量である。リベット構造は、これらの追加部品のために重くなる可能性があります。

コストと効率もまた、2つの方法の間の選択に一役買う。リベッティングは、個々のリベットのコストが低いにもかかわらず、材料費、作業費、人件費の積み重ねのために、全体としてより高価になる傾向がある。溶接は、特に自動化された工程で、よりコスト効率がよく、より速いことがある。

要約すると、リベット打ちと溶接の選択は、強度の必要性、材料の適合性、美観の考慮、および保守要件を含む用途の特定の要件に依存する。溶接は、より高い強度、より単純な設計、より速い生産を提供するが、熱歪みを導入する可能性があり、分解には柔軟性に欠ける。リベッティングは、振動に強く、分解が容易で、異種材料の接合も可能だが、一般に強度が弱く、手間がかかる。

現代工学におけるリベット接合部の一般的な用途は？

リベット接合は、その耐久性、信頼性、および他の接合方法に対する特定の利点により、現代の工学において広く利用されている。航空宇宙産業では、リベット接合は、胴体パネルや翼のような部品を接続するために重要であり、その軽量で高強度な特性は、重量を最小限に抑えながら構造的完全性を維持するために不可欠である。造船業では、リベット継手は船体や船舶の他の重要な部品を組み立てるために不可欠であり、水圧や腐食に対する耐性を提供し、水密の完全性と荒海での安全性を確保するために重要である。

建設・インフラ分野では、リベット継手は橋、タワー、ビルなどの骨組みに使用されている。これらの継手は、荷重を均等に分散し、大きな構造物に安定性を提供する能力で評価され、橋梁やトラスなどの堅牢な支持を必要とする用途に理想的です。圧力容器やボイラーでは、溶接のような熱処理が実用的でない場合や、接合部が温度変動や振動に耐える必要がある場合に、リベット接合部が好まれます。

自動車産業や公共交通産業も、特にバスやトロリーバスの車体製造において、リベット接合から利益を得ています。これらの継手は、これらの乗り物に関連する応力と振動に耐えることができる、強くて信頼できる接続を保証する。さらに、リベット接合は、台所用品やポケットナイフのような消費者製品に見られ、その強度、軽量性、耐腐食性が有利である。

全体的に、リベット接合は、経時的な緩みに対する抵抗力のため、振動や動的荷重を受ける環境で好まれる。また、取り付けに熱を必要とせず、熱膨張に強いので、温度変動を経験する産業にも適している。さらに、リベット継手は、溶接継手と比較して、検査と分解が容易であり、関係する部品への損傷が少ない。これらの特性により、リベット接合は様々な重要かつ高性能な産業で好まれる方法となっている。

リベット接続を使用する利点と欠点は何ですか？

リベット接続にはいくつかの利点と欠点があり、特定の用途に適している一方、他の用途では課題があります。

リベット接続を使用する利点は、リベットが安価で、電気や特別な材料を必要とせず、材料費とエネルギー費の両方を節約するので、費用効果が含まれる。リベットはまた、一般に溶接に比べてより少ない設備と準備しか必要としないので、生産高を増加させ、したがって必要な時間と資源を削減する。このプロセスでは、廃棄物の残渣が最小限に抑えられるため、効率が向上する。リベット接続は設計の柔軟性を提供し、検査と保守が容易である；摩耗したリベットは最小限の設備で素早く交換できる。リベットは汎用性があり、鉄と非鉄金属の両方、また木材、プラスチック、アスベスト・シートのような非金属材料を接合することができます。リベッティングは環境にも使用者にもやさしく、煙やガスを発生しないので、作業者にとって安全である。さらに、リベット接合は高い剪断強度と良好な耐疲労性を提供し、振動や衝撃力を受ける用途に適しています。

しかし、リベット接続にも欠点がある。リベット接合は、穴あけやリベットの取り付けといったいくつかの工程を伴うため、労働投入量が多くなり、人件費が増加する可能性がある。リベットは構造物に重量を加え、これは大きな構造物では大きくなり、構造効率に影響する可能性がある。リベットのために必要な穴は金属板を弱める可能性があり、穴の周囲に応力集中をもたらし、構造的完全性を維持するために板厚を追加するか、板を重ね合わせる必要が生じる可能性がある。美観上、リベット接合はより目立ち、構造から突出する可能性があり、溶接接合と比較して視覚的魅力を減少させる。リベット接合は、設置中に騒音が発生することがあり、適切に密閉されないと腐食しやすくなる可能性があるため、長期にわたるメンテナンス費用が増加する。リベット接合は、ホット・リベットまたはシーラントが使用されない限り、堅いまたは漏れのないシールを提供しない可能性があり、これは特定の用途では不利になる可能性がある。最後に、リベットは交換することができるが、その作業は面倒でうるさいことがあり、メンテナンス中にリベットを交換することは、ボルトのような他の締結方法と比べてより困難なことがある。

要約すると、リベット接合は費用効果が高く、柔軟性があるが、より高い労働要件、追加された構造重量、応力集中の問題、および美的制限が伴う。リベット接合と他の接合方法の選択は、特定のプロジェクト要件に依存する。

リベット接合部を効果的に維持・修理するには？

リベット接合部の効果的な維持と修理には、構造の完全性と長寿命を確保するためのいくつかの重要なステップが含まれる。定期的な検査が鍵であり、摩耗、腐食、疲労の兆候がないかリベット接合部をチェックする。接合部を危険にさらす可能性のある破片、汚れ、または腐食性物質を取り除くために、接合部を定期的に清掃する。保守点検で使用される空気圧リベット・ガンの清掃については、誤作動を防ぐために、エア・ホースと継手の徹底的な清掃、潤滑、点検を確実に行う。

修理に関しては、間違ったリベット・サイズや不適切な穴の準備のような欠陥を特定することから始める。リベットを交換する必要がある場合は、頭部に穴を開け、ピン・パンチを使用して、周囲の材料を傷つけることなくシャンクを折ることによって注意深く取り除く。常に正しいサイズとタイプでリベットを交換し、傾斜した頭部や亀裂のような問題を避けるために適切な取付け技術を確実にする。

ボビング、フレンチング、リング溶接のような専門技術は、特に古いリベットや損傷の激しいリベットなど、より広範囲な修理に使用できる。また、特に異種金属が関係している場合、ガルバニック腐食を防ぐために、接合部を適切にシールすることによって、潜在的な腐食に対処することが極めて重要である。

リベット接合部が過度の疲労や振動にさらされないようにしてください。金属の空隙や加工硬化を防ぐため、施工中の過度の圧縮を避ける。修理後、構造的完全性と接合部の水密性を確認するため、徹底的な試験と検査を行う。水漏れがある場合は、コーキングやリベットの調整を行い、速やかに対処する。

これらのメンテナンスと修理のガイドラインに従うことで、リベット接合部の強度、信頼性、安全性を長期にわたって維持することができます。