トランスミッションシャフトはなぜ円形なのか、不思議に思ったことはありませんか?この記事では、円形断面がねじり性能を最適化し、応力を最小化することを説明しながら、その形状の背景にある機械的な理由を掘り下げていきます。変形に強く、効率的な動力伝達を可能にするこの設計の利点について学びます。最後には、円形設計がさまざまな荷重下で機械的完全性を維持するために極めて重要である理由をご理解いただけることでしょう。円形トランスミッションシャフトが機械システムで好まれる理由となる工学原理をご覧ください。
(1) トルク記号に関する慣例
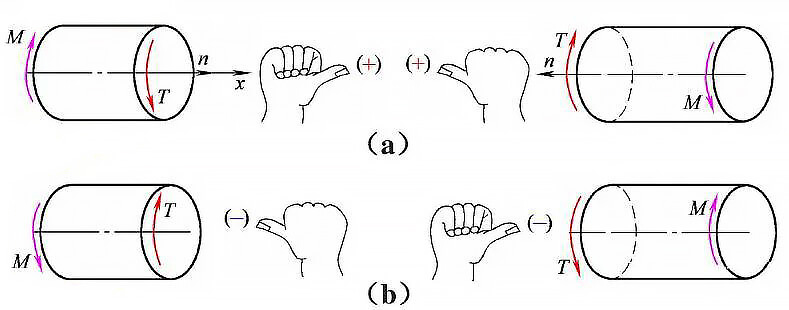
図1 トルクの方向と記号
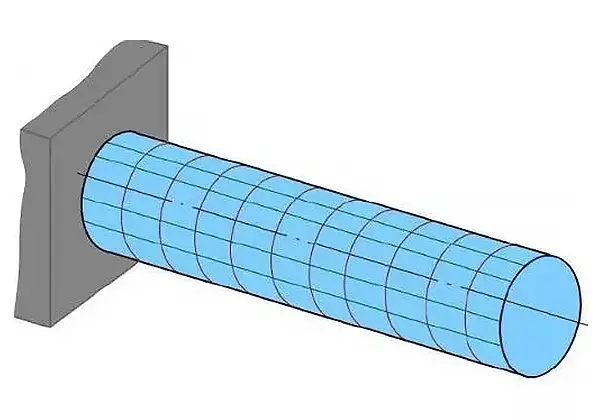
(2) 丸棒のねじり変形
断面が円形のシャフトをねじった後も、断面の形と大きさは変わらず、平らなままである。断面の半径は、断面がねじられる軸として残り、各断面は互いに小さな角度γだけ回転する。
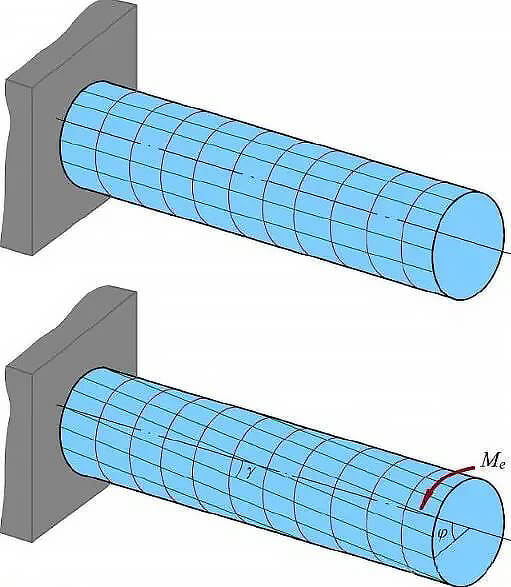
図2 丸棒のねじり変形
(3) 非円形断面バーのねじり
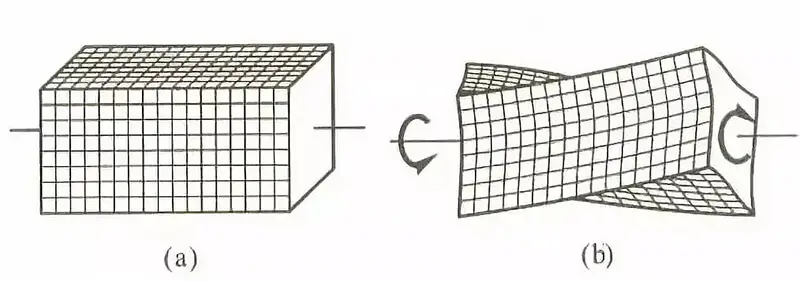
図3 角棒のねじり変形
フリー・トーション:
棒鋼の断面が非円形の場合、ねじり変形時に反りが生じる。隣接する断面の反りの程度は同じであり、棒鋼のすべての縦方向繊維の長さは変化しないことを意味する。このシナリオでは、断面に法線応力は発生せず、せん断応力のみが発生する。
自由なねじりを実現するためには、ストレートバーの両端が外部トルクを受ける必要があり、隣接する部分の反りが外部から拘束されないようにする必要がある。
拘束されたねじり:
不均一な直棒をねじると、かかるトルクの量は棒の長さ方向に変化する。棒の一端が固定されていて動かない場合、棒の隣接する部分の反りの程度は異なる。せん断応力に加えて、棒の断面には法線応力も発生する。
通常、中実棒の拘束ねじりによって生じる法線応力は小さく、無視することができる。しかし、薄肉棒鋼の場合、この法線応力は無視できないほど大きいことが多い。
(1) 平面仮説
ねじれた後、円形断面は平らなままであり、その形状、サイズ、半径は変化しない。しかし、この仮定は円形断面の軸にのみ適用され、非円形断面の軸には適用されない。
隣接するセクションの間隔は、τzx = τzy(法線応力がないことを示す)を除いて変わらない。
σ x= σ y= σ z= τ xy=0.
弾性モデルを図4に示す。

図4 直棒のねじり弾性力学モデル
(2) Mエムブレイン・アナロジー
プラントルは、一様な圧力下での薄い液膜(膜とも呼ばれる)のたるみが、等しい断面を持つ直棒のねじり問題における応力関数と数学的に類似していることを指摘した。
トーションバーとメンブレンを比較することは、ねじれの問題を解決するのに役立つ。
図5では、トーションバーの断面境界と同じ形と大きさを持つ水平な境界に、均一なフィルムが張られている。
フィルムに小さな均一な圧力を加えると、フィルムの各点に小さなたるみが生じる。
境界がある平面をxy平面とすると、サグはzで表すことができる。
フィルムは柔軟であるため、曲げモーメント、トルク、せん断力、圧力には耐えられないと仮定する。液体フィルムの表面張力と同様の一様な引張力FTに耐えるのみである。
この解析によれば、トーションバーの断面上の任意の点における、任意の方向に沿ったせん断応力は、その点における垂直方向のフィルムの傾きに等しい。
トーションバー断面の最大せん断応力は、膜の最大勾配に等しいことが観察される。しかし、最大せん断応力の方向は、最大勾配の方向に対して垂直であることに注意すべきである。
このように仮定することで、以下の表1に示す非円形断面直筋の最大せん断応力と相対ねじれ角を求めることができる。

図5 膜類似モデル
(1) 固体円形シャフト
仮定1と2の下では、構成材料が弾性範囲内にある場合の純粋なせん断におけるプラスチック材料の機械的特性:
τ= G γ,γ 剪断ひずみである;
γ=φ R/L( γは距離Lにおける2つの断面の相対ねじれ角;
φ はトーション・エンドの端面の角、Rは円の外半径、Lは2つのセクションの間隔)。

図6 中実丸棒のねじりの模式図
でのせん断応力 ρ 円形セクションの

同じトルク条件下で、円形断面の棒にかかるせん断応力(τ)は、断面の中心からの距離(ρ)に比例します。つまり、中心からの距離が大きいほど、せん断応力は大きくなります。
中心からの距離が円形断面の半径(R)に等しい場合、最大せん断応力は端部で得られる。
円形シャフトのねじり断面係数(Wp)はIP/Rで表すことができ、IPは極慣性モーメントである。この値は断面の幾何学的寸法にのみ関係し、断面積には関係しません。
最大せん断応力(τmax)は、T/WPとして計算することができる。
円形断面のソリッドシャフトの場合、ねじり断面係数(WP)は直径(D)の3乗の0.2倍にほぼ等しい。
ねじりを受ける丸棒のねじれ角(φ)は、円形断面のねじり剛性(GIP)に関係し、これはシャフトの変形に対する抵抗能力を反映する。
Lの距離にある2つのセクションの相対的なねじれ角は、ねじれの公式を使って計算することができる。
ねじれの相対角度:
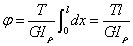
円形シャフトの剛性条件:

(2) 中空円形シャフト
中空円形シャフトの断面ねじり係数は約WP ≈ 0.2D3 (1- α 4),0<α=d/D<1。
α=0.8の場合、WPは中実円形断面の60%となり、同じトルクでは強度は40%低下するが、同じ材質と長さでは重量差は2.8倍となる。
(3) 閉じた薄肉チューブ
肉厚(a)が半径(R0)よりもはるかに小さい丸パイプは、薄肉丸パイプとして知られている。この種のパイプは、どのような形状のものでも、断面が等しいものでもよい。
薄肉管であるため、せん断応力は肉厚(t)全体に一様に分布すると仮定して近似解を求める。
せん断応力の逆数則を適用すると、パイプ断面上のすべての点とパイプ壁の平均軸方向せん断応力の積は等しく、すなわちせん断流(q)は一定であると結論づけることができる。
qの値は断面全体で一定であるため、最大せん断応力は最小肉厚部で発生する。
パイプ断面が円形の場合、その面積(Am)はπR0²に等しい。円筒の直径を大きくすると、せん断応力を大幅に減少させることができます。

図6 いくつかの一般的な断面のせん断応力分布
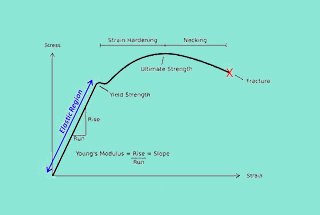
ねじり試験では、試験片の断面全体に不均一な応力分布が生じます。表面が最も大きな応力を受け、中心に向かうにつれて応力は減少します。
その結果、材料にねじれが生じると、損傷は丸棒の最外層から始まり、内部に向かって進行する。亀裂は表層から始まり、内側に伝播する。
エンジニアリングの分野では、ねじり試験は一般的に表面欠陥とその性能を調べるために利用されている。 表面硬化 素材の層。
図7に示すように。

図7 丸棒サンプルのねじり試験
低炭素鋼などの塑性材料で作られた円形シャフトのねじり加工では、まずシャフトの表面が降伏し、ねじり変形が大きくなるにつれて断面に沿って円周が切断される。
これは、材料のせん断耐力が引張耐力より低いためで、最大せん断応力が断面に発生し、せん断破壊に至る。
工学では通常、断面外縁の最大せん断応力を材料のせん断降伏限界(τs)とし、これを危険状態として強度条件を設定する。
しかし、エッジのせん断応力が降伏限界に達しても、他の部品はまだ線形弾性加工状態にあり、丸棒は明らかな塑性変形を起こさず、トルクを増加させ続けることができる。
材料の塑性変形を考慮すると、中実丸棒の極限トルク(塑性トルク)は降伏トルク(工学的な簡易計算の結果)より1/3大きい。
材料断面端のせん断応力が材料のせん断降伏限界τsに達すると、ねじりカップルモーメントの増加とともに塑性領域が徐々に内側に拡大し、断面端の材料が強化され始める。
ねじり結合モーメントが増加し続けると、亀裂は丸棒の最外層から始まり、最終的には断面に沿ってせん断する。
図8に示すように。

図8 プラスチック丸棒サンプルのねじり試験
鋳鉄など、せん断能力よりも引張能力の低い脆性材料で作られた丸シャフトでは、ねじり破壊時の変形は最小です。シャフトは、軸に対して約45°の角度でヘリカル面上で破断する傾向がある。
これは、軸に対して135°の傾斜面が最大の引張応力を受けるからです。この部分の最大引張応力が材料の引張強さの限界を超えると、シャフトはこの部分の張力によって破損します。
図9に示すように。

図9 脆性材料丸棒サンプルのねじり試験
丸太棒が受ける内部トルクTは、断面にせん断応力の半径方向の線形分布を発生させるだけでなく、軸平面に沿って対応するせん断応力を誘発し、軸平面に沿って亀裂を生じさせる可能性がある。
木材は異方性材料であるため、軸方向に沿って繊維に平行なせん断力は、断面において繊維に垂直なせん断力よりもはるかに小さく、その結果、図10に示すような割れパターンが生じる。

図10 丸太のねじり破壊
図は、弾性理論の解析による正方形、三角形、楕円形の断面の最大応力とねじれ角の計算式を示している。
前述のすべてのケースで、最大せん断応力は中心軸に最も近い断面境界線で発生する。
閉じた薄肉パイプの場合、中心軸に対して最も肉厚の薄い位置が最も高いせん断応力を受ける。

図11 各種断面のねじりせん断応力と相対ねじり角の計算式
同じトルクTを受ける円、正方形、三角形、楕円の面積をSとする。
正方形の辺の長さはa = √Sであり、正三角形の辺の長さはおよそa≈2.3√Sである。
図に示した最大応力計算式を用いると、同じ断面積とトルクを受けた場合、正三角形の断面にかかる最大せん断応力は正方形の約1.8倍となる。
a=bで円になる楕円の場合、a=0.56√Sとなり、正方形の最大せん断応力は円の約1.32倍となる。
楕円がa≠bであり、1>b/a=λ>0である場合、楕円上の最大せん断応力と円上の最大せん断応力の比はλ√S-2となる。したがって、λの値が小さいほど、せん断応力は大きくなる。
以上の比較を通じて、次のように結論づけることができる:
シャフトが同じ断面を持ち、同じトルクを負担する場合、円形断面の最大せん断応力は非円形断面に比べて最も小さくなる。さらに、ねじれ角も小さくなります。したがって、円形トランスミッションシャフトは、ねじり機械的性能において当然有利である。
これらの知見を任意の断面に拡張すると、円形断面のシャフトが最も効率が高いことが証明できる。
シャフトが同じ断面を持ち、同じトルクを負担する場合、円形断面の最大せん断応力は非円形断面に比べて最も小さくなる。さらに、ねじれ角も小さくなります。したがって、円形トランスミッションシャフトは、ねじり機械的性能において当然有利である。
これらの知見を任意の断面に拡張すると、円形断面のシャフトが最も効率が高いことが証明できる。
表1 シャフト径のトルクチェック式
|
車軸タイプ |
フォーミュラ |
インストラクション |
|
ソリッドシャフト |
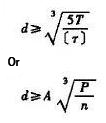 |
どこでだ: d - 断面におけるシャフトの直径を計算する。 (mm) シャフトが伝達するT定格トルク (N・mm) T=9550000P/n シャフトが伝達するP定格出力 (kW) n軸回転数(R/分) [T] - シャフトの許容せん断応力 (MPa) A - [t]によって決まる係数、 中空円形シャフトの内径d0と外径DのV比 |
|
中空軸 |
 |
円形断面のシャフトの表面せん断応力は高く、ねじり荷重を受ける中心部は比較的小さい。したがって、中心部で十分な役割を果たさない材料の一部を除去することで、シャフトの重量を効果的に軽減し、耐曲げ性を向上させることができる。
しかし、シャフト部品を中空にするかどうかを決めるには、機械的な要因だけでなく、技術的なコストや製造コストも考慮する必要がある。肉厚が薄すぎると、局部的なひだが発生し、ベアリング能力が低下する可能性があることに注意することが重要です。
円筒の肉厚(δ)が半径(R0)よりはるかに小さい場合、一般に≦R0/10とされ、薄肉円筒と呼ばれる。しかし、薄肉円筒に軸方向に開口部を設けると、ねじり抵抗が著しく低下する。そのため、通常はダイアフラムを追加してねじり抵抗を改善する。 硬さと強さ.
シャフトは通常、様々なセクションから構成されており、これらのセクション間の移行位置での応力集中は、シャフト部品の故障の一般的な原因となっている。
隣接する2つのセクションとトランジション・フィレットの大径の選択と決定方法については、文献を参照することができる。
円筒形コイルばねは、機械工学では一般的な部品で、らせん状の軸と大きな弾性変形が特徴である。
をデザインする。 春 高荷重のスプリングの場合、一般的に強度が第一に考慮されます。しかし、耐荷重が低いスプリングの場合、一般的に変形を考慮する必要があります。
それほど重要でないスプリングの場合は、構造寸法と仕様のみに基づいて選択することができます。
ばねの設計と計算方法については、GB/T1239シリーズ規格、GB/T2089、DIN2089などの関連文献をご参照ください。
静的荷重の作用下では、ねじりと引っ張りの力学的特性には一定の関係がある。σ許容せん断応力[τ]:材料の[τ]を使用する。
| 素材タイプ | [σ] | [ τ] | [ τ] |
| プラスチック | 1 | 0.5~0.7 [σ] | 0.55または0.577σ] |
| 脆い素材 | 1 | 0.7~1.0 [σ] | 0.8~1.0 [σ] |
上の表は、文献に記載されているせん断応力と法線応力の関係が異なることを強調している。
文献に記載されているいくつかの塑性材料は、せん断応力と法線応力の比が0.5~0.7[σ]であるべきことを示している。
ただし、この関係は概算であり、正確なせん断応力データが入手できない場合にのみ使用すべきである。
正確な検証のためには、材料のねじり強さの具体的な値を得ることが必要である。