1.実験材料 1.1 材料性能パラメータ 実験では、化学組成を表 1 に、性能パラメータを表 2 に示す DP590 高強度鋼を使用した。表 1 材料の化学組成(質量分率) 材料グレード C Si Mn P S Al Ti DP590 0.078 0.03 1.76 0.01 0.004 ≥ 0.020 - 表 2 材料性能パラメータ パラメータ値 加工硬化指数 n|0.13 ポアソン比 μ 0.33 弾性率 E/MPa 199 000 硬化指数 K 1 003 降伏強さ/MPa 318 引張強さ/MPa 626 降伏-引張比/% 50 1.2 応力-ひずみ曲線 引張試験はGB/T 228.1-2010試験規格に従って実施し、[...]した。

実験では、化学組成を表1に、性能パラメータを表2に示すDP590高張力鋼を使用した。
表1 素材の化学組成(質量分率)
| 素材グレード | C | Si | ムン | P | S | アル | ティ |
| DP590 | 0.078 | 0.03 | 1.76 | 0.01 | 0.004 | ≥ 0.020 | – |
表2 素材性能 パラメータ
| パラメータ | 価値 |
| 作業硬化指数 n | 0.13 |
| ポアソン比 μ | 0.33 |
| 弾性率 E/MPa | 199 000 |
| 硬化指数 K | 1 003 |
| 降伏強さ/MPa | 318 |
| 引張強さ/MPa | 626 |
| 降伏張力比/% | 50 |
引張試験はGB/T 228.1-2010試験規格に従って実施し、試験データから得られた真の応力-ひずみ曲線を図1に示す。

NUMISHEET2011の国際標準ケースと、実生産でよく使われる梁部品のサイズから、コの字型部品に使われる板のサイズを100mm×360mm×1.2mmと決定。
組み立てられた二次元構造を図 2 に、金型部品の幾何学的寸法を表 3 に示す。図面に従ってUG NXソフトウェアでモデルを作成し、爆薬構造を図3に示すように組み立てた。
その後、図4に示すように、Dynaformにインポートしてメッシュ作成と基本的なプロセス・パラメーターの設定を行った。

表3 金型部品の幾何学的寸法
| パラメータ | 寸法/mm |
| W1 | 80 |
| W2 | 84 |
| W3 | 135 |
| W4 | 135.5 |
| R1 | 5.0 |
| R2 | 7.0 |
| G1 | 1.2 |
| ストローク | 70 |


プレス加工中、シートメタルは大量の弾性変形を受ける。
スタンピングの最終段階では、荷重が除かれることにより、先に発生した弾性エネルギーが放出され、その結果、プレスの強度が低下する。 内部応力 が再結合し、部品の形状が変化する。その結果、板金のスプリングバック欠陥が生じる。
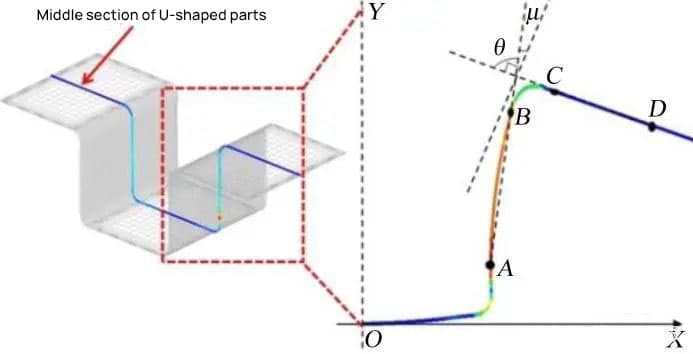
ここで、U字の真ん中の部分を選び、その部分を測定する。 スプリングバック 図5のような状況だ。
スプリングバックの大きさは、表面ABとCDの間の角度θの補角μによって特徴付けられる。角度μが大きいほど、スプリングバックの振幅は大きくなります。
プレス部品のスプリングバックに影響を与える要因は主に以下の通りです。 金型構造板金形状と機械的特性、スタンピングプロセスパラメーター。
構造およびスタンピングの観点から プロセス特性 U字形状部品のフランジ力、摩擦係数、板金厚、パンチコーナー半径の4つの主要因を選択し、スプリングバック角度の変化に及ぼす各因子の影響を探った。
板厚1.2mm、摩擦係数0.125の高強度鋼DP590を使用し、パンチとダイの隙間(G1)を1.2mmとした条件下で、フランジ力を10kNから120kNまで変化させて成形シミュレーションとスプリングバックシミュレーションを行い、フランジ力がスプリングバックに及ぼす影響を調べた。
シミュレーションによって得られたスプリングバック角に対するフランジング力の影響を表4と図6に示す。
表4 フランジング力とスプリングバックの関係。
| フランジ力/kN | スプリングバック角(°) |
| 10 | 8.126 |
| 20 | 8.902 |
| 40 | 7.734 |
| 60 | 6.660 |
| 80 | 5.572 |
| 100 | 4.226 |
| 120 | 3.686 |

図6に示すように、部品のスプリングバック角は最初に増加し、その後減少する。表4から、フランジング力を10kNから120kNまで変化させた場合、スプリングバック角の最大変化量は5.216°であり、フランジング力の制御がスプリングバック角により明確に影響していることがわかります。
上記の現象の理由は、フランジ力が小さい場合、部品は主に曲げによって形成されるからである。板金はパンチの作用で曲げ応力を発生させ、パンチが負荷を解除した後に曲げ応力が解放されるため、スプリングバックが増加する。
フランジング力がある程度大きくなると、材料の塑性変形が大きくなり、板金が解放する弾性変形量が減少するため、スプリングバックも小さくなる。
フランジ力40kN、パンチとダイの隙間1.2mmという条件下で、摩擦係数0.025~0.275の成形シミュレーションとスプリングバックシミュレーションを行い、摩擦係数がスプリングバックに及ぼす影響を調べた。
シミュレーションで得られたスプリングバック角に対する摩擦係数の影響を表5と図7に示す。
表5 摩擦係数とスプリングバックの関係。
| 摩擦係数 | スプリングバック角(°) |
| 0.025 | 8.126 |
| 0.075 | 8.902 |
| 0.125 | 7.734 |
| 0.175 | 6.660 |
| 0.225 | 5.572 |
| 0.275 | 4.226 |

表5から、摩擦係数が0.025から0.275まで変化した場合、スプリングバック角の最大変化量は4.676°であり、摩擦係数の制御がスプリングバック角により顕著な影響を及ぼすことがわかる。
図7に示すように、板金のスプリングバック角は、摩擦係数の増加とともに最初に増加し、次に減少する。
上記の現象の理由は、当初は摩擦係数が小さいため、材料の摩擦抵抗が小さく、板金の成形工程は主に曲げ加工であるため、スプリングバックが大きくなる。
摩擦係数が徐々に大きくなると、材料の摩擦抵抗も大きくなる。摩擦抵抗が十分に大きいと、板金の端は動きにくくなり、部品の成形工程は主に塑性変形となる。
パンチが無負荷になった後、シートメタルはより少ない弾性ポテンシャルエネルギーを放出するため、シートメタルのスプリングバックは減少する。
フランジ力40kN、パンチとダイの隙間1.2mm、摩擦係数0.125、パンチ半径R5mmという条件下で、板厚1.0mmから1.8mmまでの成形シミュレーションとスプリングバックシミュレーションを行い、板厚がスプリングバックに及ぼす影響を調べた。
シミュレーションで得られたスプリングバック角に対する板金厚の影響を表6と図8に示す。
表6 板厚とスプリングバックの関係。
| 板金厚/mm | スプリングバック角(°) |
| 1 | 10.541 |
| 1.2 | 7.734 |
| 1.4 | 5.448 |
| 1.6 | 3.814 |
| 1.8 | 2.030 |

表6に示すように、板厚が1.0mmから1.8mmまで変化した場合、スプリングバック角の最大変化量は8.511°までであり、これは選択した4つの因子の中で最も大きく、板厚の制御がスプリングバック角に比較的明らかな影響を及ぼすことを示している。
図8に示すように、板金のスプリングバック角は板金厚の増加とともに減少する。
これは主に、パンチ半径が一定の条件下では、板金厚が大きくなるほど、パンチ半径の比率が小さくなるためである。 曲げ半径 その結果、板金の曲げ変形が少なくなり、全変形に占める弾性変形の割合が低くなる。
したがって、パンチが無負荷になると、シートメタルのスプリングバックは減少する。
フランジ力40kN、摩擦係数0.125の条件下で、パンチコーナー半径R3mmからR7mmまでの成形シミュレーションとスプリングバックシミュレーションを行い、パンチコーナー半径がスプリングバックに及ぼす影響を調べた。
シミュレーションで得られたスプリングバック角に対するパンチコーナー半径の影響を表7と図9に示す。
表7 パンチコーナー半径とスプリングバックの関係。
| パンチフィレットの半径/mm | スプリングバック角(°) |
| 3 | 6.388 |
| 4 | 6.982 |
| 5 | 7.734 |
| 6 | 8.153 |
| 7 | 8.553 |

表7と図9の観察によると、パンチフィレットの半径を3mmから7mmにすると、スプリングバック角は6.388°から8.553°に増加する。
この挙動は、パンチフィレットとシートメタルの接触面積が増加し、その結果、曲げ変形が大きくなり、スプリングバック効果が大きくなったことに起因している。
とはいえ、表7から、パンチフィレット半径が3mmから7mmに変化した場合のスプリングバックの最大値の変化はわずか2.165°であり、これは選択された4つの要因の中で最も小さい影響であることがわかります。
これは、スプリングバック角に対するパンチフィレット半径の影響が最小であることを意味する。