真直度測定：プロのような計算方法

1. はじめに

ガイドレールの真直度誤差を評価する方法としては、両端連結法と最小条件法の2つが一般的に用いられている。

両端点接続法は、誤差曲線を端から端まで接続し、曲線の最高点と最低点に端から端までの線に平行な2本の線を引き、2本の平行線の間の縦軸に沿った値を測定する。

データ処理後の値がガイドレールの真直度誤差となる。

最小条件法は、誤差曲線の「高、高」（または「低、低」）点を結び、低（高）点を通るそれに平行な線を引く。

縦軸に沿った2本の平行線の間で測定された値が、データ処理後のガイドレールの真直度誤差となる。

最小条件法は仲裁評価である。

両端点接続法は仲裁評価ではないが、時には大きな誤差を生むこともあるが、評価が簡単で便利なため、本番では一般的に使用されている。

この記事では、これら2つの評価方法の間に生じる誤差の限界値について論じる。

2. 誤差曲線は線の両端と同じ側にある

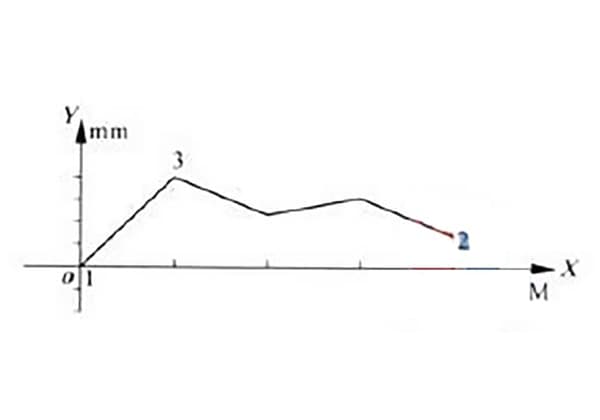
あるモデルの油圧スライドレールガイドの真直度誤差を測定したところ、図1に示すような真直度誤差曲線が得られた。

図からわかるように、誤差曲線は線の両端と同じ側にある。

以下では、最小条件法と両端連結法を用いて、ガイドレールの真直度誤差値を評価する。

(1) 最小条件法による真直度誤差の評価

最小条件法によれば、図1の曲線の最低点1と2（最低点1は原点と一致）は、図2に示すように直線a1a1で結ばれる。

直線a1a1に対して最高点3を通る平行線a2a2を引く。

データ処理後、2本の平行線a1a1とa2a2で囲まれた領域でy軸に沿って測定した値が、最小条件法から得られるガイドレールの真直度誤差δを表す。

(2) 両端接続法による真直度誤差の評価

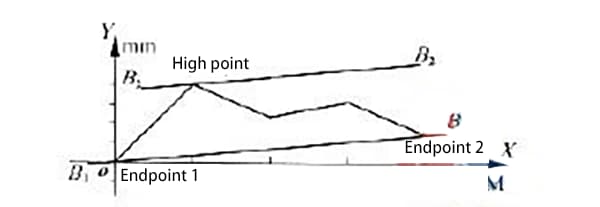
両端接続法によれば、図1に示す曲線の両端は、図3に示すように、曲線の端点1と端点2でもある。

端点1と2は直線b1b1で結ばれ、最高点を通る平行線b2b2が引かれる。

データ処理後、2本の平行線b1b1とb2b2で囲まれた領域でy軸に沿って測定した値が、両端接続法で得られたガイドレールの真直度誤差δを表す。

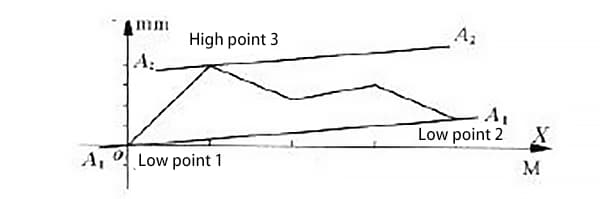
(3)2つの評価方法で発生する誤差の限界の決定

同じガイドレールの真直度誤差を両評価方法で求めるので、図2の「低点1」、「低点2」、「高点3」は、それぞれ図3の「終点1」、「終点2」、「高点3」に対応する。これにより、線分a1a1は線分b1b1と一致し、線分a2a2は線分b2b2と一致する。

したがって、2つの評価方法によって生じる誤差はゼロとなる。

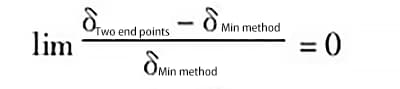
以上の分析から、誤差曲線が直線の両端と同じ側にある場合、2つの評価方法によって発生する誤差限界はゼロであり、2つの方法によって得られる評価結果は同じであることを意味する。

3.誤差曲線は両端を結ぶ線の両側にある。

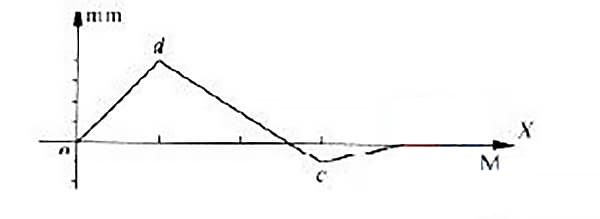
測定されたガイドレールの真直度誤差曲線には、図4に示すように、両端を結ぶ線の両側に誤差曲線が存在するものがある。

このガイドレールの誤差曲線は、両端を結ぶ線がX軸と一致している。ガイドレールの真直度誤差は、最小条件法と両端接続法を用いて評価する。

図4からわかるように、o点とc点は曲線の2つの低点と2つの端点であり、d点は最高点である。

最小条件法によれば、点oと点cは図5に示すように直線a1a1で結ばれる。線分a2a2は最高点dを通り線分a1a1に平行に引かれる。

データ処理後、2本の平行線a1a1とa2a2で囲まれた領域でy軸に沿って測定した値が、最小条件法から得られるガイドレールの真直度誤差δを表す。

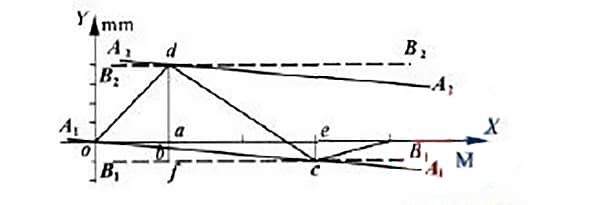
2点接続法に従い、点Cと点Dをそれぞれ通るX軸に平行な2本の直線を引く。

これらの線は、図5の点線b1b1とb2b2で表されている。この2本の平行線で囲まれた領域において、データ処理後にy軸に沿って測定された値が、2つの端点間のガイドレールの真直度誤差値を表す。

2つの端点における最小偏差法と偏差値を決定するために、点Dを通り、点Aで軸と交差し、点Hで線a1a1と交差し、点Fで線b1b1と交差するy軸に平行な線を引く。

同様に、点Cを通り、点Eで軸と交差するY軸に平行な線を引く。

(1) 最小条件法による真直度誤差の測定

最小条件法によれば、ガイドレールの真直度誤差値δは、データ処理後のy軸方向の測定値から導出される。

図5に示すとおりである：

そして、BD＝BA＋ADである、

∆したがって、△OABと△OECは2つの相似三角形である、

式（3）を再整理するとこうなる：

式（4）を式（2）に代入し、並べ替えるとこうなる：

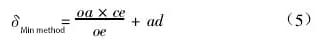
(2) 2点接続法による真直度誤差の測定

2点接続法によれば、データ処理後にy軸に沿って測定された値は、2つの端点間のガイドレールの真直度誤差値δを表す。

図5に示すとおりである：

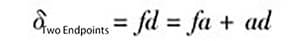
そして、ファ＝セである、

(3) 2つの評価方法による誤差値の算出

式(6)から式(5)を引いたもの、

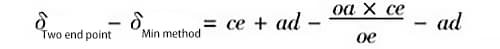
並べ替えるとこうなる：

(4) 2つの評価方法による最大誤差の算出

図5において、ad＝δ1、ce＝δ2、oa＝pとし、測定するガイドレールの長さをlとすると、oe＝l-pとなる：

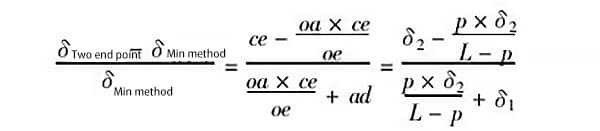
たとえば、p＝0.5m（すなわちピッチが0.5m）、δ1＝1.0δ、δ2＝0.25δ、測定されたガイドレールの長さがl-2mのとき、2つの評価方法で発生する誤差の比率は次のようになる：

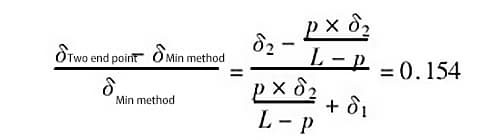
2つの評価方法で発生する誤差の比率は0.154であり、これは2点接続法で発生する誤差が最小条件法で発生する誤差より15.4%大きいことを意味する。

上記の式において すなわち、誤差曲線の最高点と最低点は無限に離れている。だから、こうなる：

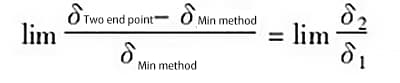
例えば、δ1＝1.0δ、δ2＝0.25δで、誤差曲線の最高点と最低点の距離が無限に離れている場合（つまりL＝0.25）、2つの評価方法で発生する誤差の比率は つまり、2点接続法で発生する誤差は、最小条件法で発生する誤差よりも25%大きい。

図6に示すように、δ1＝δ2、すなわち誤差曲線の最高点と最低点の距離が等しい場合、2つの評価方法によって生成される誤差の最大値は次のようになる：

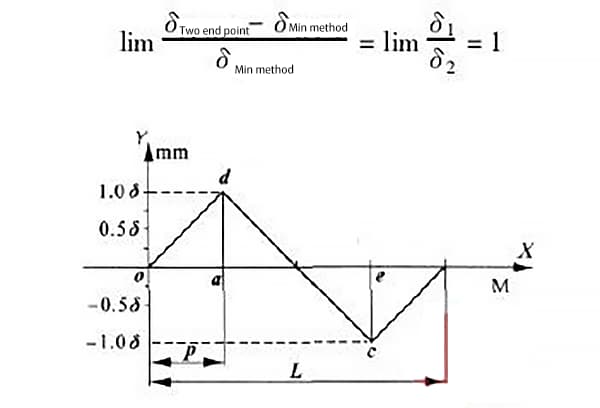
このことから、ガイドレールの最高点と最低点が等しく、無限に離れている場合、2つの評価方法で発生する最大誤差が最も大きく、100%に達することがわかる。

表1は、誤差曲線点が2点接続線の両側に分布している場合、測定されたガイドレールの長さが異なる2つの評価方法によって発生する誤差の比率を示している。

誤差曲線の最高点と最低点の間の距離は、測定ピッチp=0.5のときに等しくなる。

表1 2つの評価方法の誤差率

エラー率	ガイドレールの最高点と最低点の間の距離L（M）
1	10	15	20	25	30	40	∞
	33.30%	90%	93.30%	95%	96%	96.70%	97.50%

4.結論

真直度誤差曲線上の点が2点接続線の同じ側にある場合、2つの評価方法によって発生する誤差はゼロ、つまり2つの評価方法から得られる結果は同じである。

真直度誤差曲線上の点が2点接続線の両側にあり、誤差曲線の最高点と最低点が等しく、無限に離れている場合、2つの評価方法によって発生する誤差の最大値は最も大きくなり、2点接続法によって発生する誤差は、最小条件法によって発生する誤差よりも100%高くなる可能性がある。

したがって、大型工作機械用ガイドレールの真直度誤差を実生産で評価する場合、適切な評価方法を選択することが非常に重要である。誤差曲線上の点が2点接続線の両側にある場合は、最小条件法を第一選択として評価する。