材料力学における強度と剛性の理解

序文

機械システムや構造物の最適な性能と信頼性を確保するためには、各コンポーネントが意図された機能を効果的かつ効率的に果たす必要があります。工学的な部品安全設計の主な目的は、すべての要素が適切な強度、剛性、安定性を持つことを保証し、それによってシステム全体の完全性と寿命を保証することです。

安定性とは、工学における基本的な概念であり、外力を受けたときに元の平衡状態を維持または回復する部品の能力を指す。この原理は、以下のような様々な場面で重要である：

1. 軸圧縮を受けた細長い柱の急激な横たわみ（オイラー座屈）
2. 建物の柱が耐力破壊により倒壊すること（構造的不安定性）
3. 圧縮応力またはせん断応力下での薄肉部材の座屈（局部座屈または全体座屈）

これらの例は、致命的な故障を防ぎ、機械システムや構造物の安全な運転を確保する上で、安定性が重要であることを示している。

このディスカッションでは、同様に重要な2つの工学原理、剛性と強度についての包括的な理解を深めることに重点を置きます。これらの概念は、安定性とともに、コンポーネントの安全設計における基本的な考慮事項の3要素を形成し、それぞれが工学システムの全体的な性能、耐久性、安全性を決定する上で重要な役割を果たします。

強さ

強さとは何か？

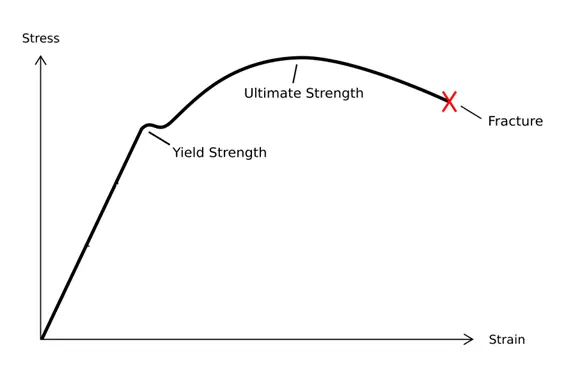
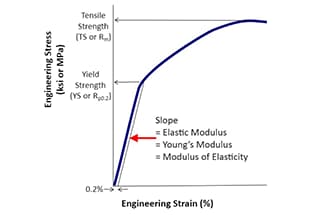
定義強度とは、材料、部品、構造物が、破壊、過度の変形、損傷を起こすことなく、加えられる荷重や力に耐える能力のことである。材料科学および工学における基本的な特性であり、機械的応力に抵抗する材料の能力を決定する。

強さにはさまざまな側面がある：

1. 引張強さ：材料が破断する前に伸張力を受けたときに耐えられる最大応力。
2. 圧縮強さ：材料が圧縮力を受けたとき、破壊するまでに耐えられる最大応力。
3. 降伏強さ：材料が塑性変形し始める応力。
4. せん断強さ：力の方向に平行な平面に沿って材料の内部滑りを引き起こす力に抵抗する能力。

例えば、金属加工では、材料の強度を理解することが、使用荷重に耐える部品を設計する上で極めて重要です。ビルの鉄骨梁は、曲げたり折れたりすることなく、構造物の重量と追加荷重を支えるのに十分な強度を持たなければならない。

強さは様々な要因に影響される：

• 材料組成と微細構造
• 熱処理および加工方法
• 環境条件（温度、腐食）
• 負荷率および負荷時間

強度の測定単位は通常、帝国単位ではメガパスカル（MPa）またはポンド毎平方インチ（psi）で表される。例えば、軟鋼の引張強さは約400～550MPaだが、高強度合金鋼は1000MPaを超えることもある。

製造業やエンジニアリングの分野では、強度計算と試験が不可欠である：

• 特定の用途に適した材料の選択
• 最適な性能と安全性を備えた部品の設計
• 製品寿命と故障モードの予測
• 業界標準および規制へのコンプライアンスの確保

有限要素解析（FEA）や破壊試験などの高度な技術は、複雑なエンジニアリング用途における材料や部品の強度を評価・検証するためにしばしば採用される。

強度に基づく故障の種類

脆性破壊： 最小限の塑性変形で急速に亀裂が進展することを特徴とする、突発的で破局的な破壊モード。このタイプの破壊は前触れもなく発生し、通常、きれいで平坦な破壊面になる。

例えば、こうだ：

1. 一軸引張試験中に鋳鉄試験片が断面に沿って突然破壊することで、破壊面に結晶のような外観を示す。
2. ねじり試験中に断面が円形の鋳鉄試料が斜めの平面に沿って突然破壊し、ヘリカル破壊パターンを示す。

プラスチック収量： 材料が著しい塑性変形を起こし、永久的な形状変化と構造的完全性の喪失をもたらす破壊様式。このタイプの破壊は一般に、脆性破壊に比べてより緩やかで観察可能である。

例えば、こうだ：

1. 引張試験中、低炭素鋼の試験片は、特徴的なカップ・アンド・コーンの破断面を伴って、極限破壊の前にかなりのネッキングと伸びを示す。
2. ねじりでは、低炭素鋼のサンプルは破損する前に大きな角度変形と反りを経験し、しばしば目に見える表面の歪みを伴います。

材料の破壊モードは、材料特性、荷重条件、温度、環境要因など、さまざまな要因によって異なることに注意することが重要です。材料によっては、低温や高いひずみ速度などの特定の条件下で、延性から脆性への移行を示す場合があります。

ストレングス理論

1.最大引張応力理論：

一方向応力条件下で、部材のある点の最大引張応力σ1が極限応力σbに達すると、材料は脆性破壊を起こす。したがって、複雑な応力条件下での臨界点を持つ部材の脆性破壊の基準は、σ1 = σbとなります。

その結果、第一次世界大戦で確立された強さの条件が満たされることになる。 強度理論 はσ1≦σbである。

2.最大引張ひずみ理論：

一方向応力条件下で最大引張ひずみε1が限界値εuに達すると、材料は脆性破壊によって破壊する。これはε1＝εuと表すことができる。

一般化されたフックの法則から、ε1は次のように計算できる：ε1 = [σ1 - u(σ2 + σ3)] / E ですから、σ1 - u(σ2 + σ3) = σb となります。

第2の強度理論によって確立された強度条件は、σ1 - u(σ2 + σ3) ≤ σbである。

3.最大せん断応力理論：

一方向応力条件下で最大せん断応力τMaxが極限せん断応力τ0に達すると、材料は降伏によって破壊する。これはτMax = τ0と表すことができる。

軸引張時の傾斜断面のせん断応力の式は、τ0 = σs/2（σsは断面の法線応力）です。τMaxの式は（σ1 - σ3）/2である。したがって、損傷条件はσ1 - σ3 = σsと書き換えることができる。

第3の強度理論によって確立された強度条件は、σ1 - σ3 ≦ σsである。

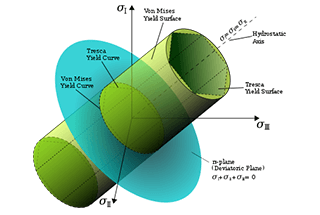
4.形状変化比エネルギー理論

一方向応力条件下で、部材のある点における形状変化率が限界値に達すると、材料は降伏により破壊する。

第4の強度理論によって確立された強度条件は次の通りである：

√(σ1^2 + σ2^2 + σ3^2 - σ1σ2 - σ2σ3 - σ3σ1) < σs.

2.剛性

硬さとは

定義：剛性とは、外力を受けたときに弾性変形や変位に抵抗する材料、部品、構造の能力を指す。加えられる荷重の下で、システムがその形状や寸法を許容範囲内に維持できる程度を定量化したものである。

剛性は、材料や構造物における力と変形の関係を特徴付ける、工学における基本的なパラメータである。剛性は、加えられる力と結果として生じる変位の比として定義され、単位変形を生じさせるのに必要な力の量を示します。数学用語では、剛性（k）は次式で表されます：

k = F / δ

どこでだ：

• F = 加えられる力
• δ＝結果として生じる変位

剛性の単位は通常、単位長さ当たりの力で、SIシステムではN/m（ニュートン毎メートル）、インペリアルシステムではlbf/in（ポンド毎インチ）など。

実用的な用語では、剛性はバネに例えて概念化することができます。バネの硬さを表すバネ定数は、加えられた引張力または圧縮力と、結果として生じる伸びまたは圧縮の比率として定義されます。この関係は線形弾性系のフックの法則で記述されます。

剛性を理解し制御することは、以下のような様々な工学的用途において極めて重要です：

1. 構造設計：建物や橋が過度に変形することなく荷重に耐えられるようにすること。
2. 機械部品：使用荷重下で精度を維持する部品の設計
3. 振動制御：繰り返し荷重に対するシステムの動的応答の管理
4. 材料の選択：剛性特性に基づいて、特定の用途に適切な材料を選択する。

エンジニアは、剛性要件と、強度、重量、コスト、製造性といった他の設計上の考慮事項とのバランスを取り、特定の用途に最適なソリューションを作り出さなければなりません。

剛性タイプ：

印加される荷重が一定の場合、静的剛性と呼ばれる。

荷重が交互にかかる場合は、動的剛性と呼ばれる。

静的剛性には、構造剛性と接触剛性が含まれる。

構造剛性とは、部材自体の剛性を指し、曲げ剛性とねじり剛性が含まれる。

1.曲げ剛性：以下の式に従って計算される：

K=P/δ

どこ

• P - 静荷重（n）；
• δ・・・荷重方向の弾性変形（μm）．

2.ねじり剛性は以下の式に従って計算される：

K_m=ML/θ

ここで、M - 印加トルク（n - m）；

L - トルク作用位置から固定端までの距離（m）；

θ...ねじれ角（°)

3.強度と剛性の関係

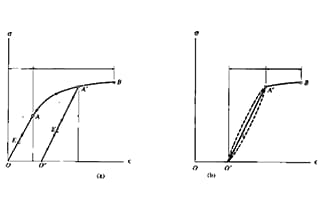
上記の強度と剛性の説明から、強度は外力による破壊に焦点を当て、塑性降伏破壊と脆性破壊破壊に分類され、引張試験中の応力-ひずみ曲線に関係することがわかります。これに対し、剛性は変形と力の関係に関係します。

図に示すように。

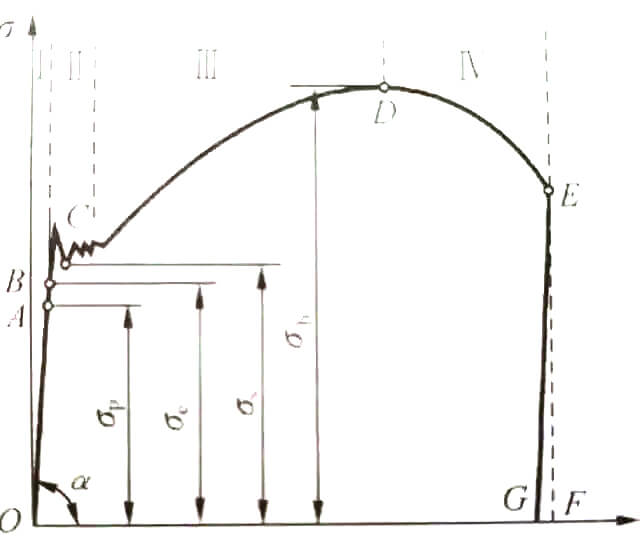
図の曲線は4段階に分けられる：

1.弾性変形段階；

2.収穫期；

3.強化段階；

4.局所ネッキングステージ。

剛性は弾性変形に対する抵抗と定義され、初期段階で発生し、弾性条件下ではフックの法則に支配される。

以下の条件下での曲げ剛性とねじり剛性の計算 静荷重 はフックの法則に似ており、剛性は弾性変形段階でのみ測定されることを示唆している。

次の段階として、引張試験中に塑性変形が起こると、残留ひずみは消えない。応力-ひずみ曲線では、応力はほとんど変化しないものの、ひずみは大きく増加します。この時点で応力は降伏限界に達し、材料は塑性降伏破壊の段階に入ります。応力が増加し続けると、ひずみも強度限界に達するまで増加します。

したがって、強度の測定は、材料が弾性変形を起こした後、強度の限界に達する前に行われる。

包む

結論として、部品の破損段階では剛性と強度の両方が評価され、剛性は応力によって、強度は変形によって測定される。

変形過程におけるその順序は、剛性は早い段階で発生し、強度は遅い段階で発生する。

したがって、部品の破損条件を評価する場合、剛性要件が満たされている限り、部品は弾性変形段階で十分な応力に耐えることができ、ひいては強度要件を満たすはずである。

この関係は、機械装置のシャフトなど様々な設計に反映される。通常、シャフトのサイズは強度条件に基づいて決定され、次に剛性条件に基づいてその剛性が検証される。

そのため、精密機械用シャフトの剛性要件は非常に高く設定されており、その断面寸法の設計は剛性条件によって制御されることが多い。