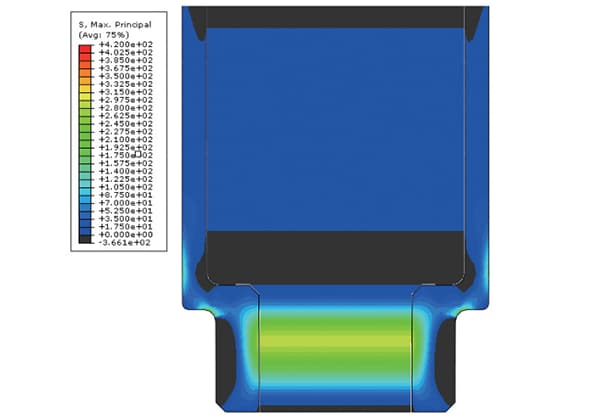
金属部品を切断することなく、その部品がどれだけの応力に耐えられるかを正確に知ることができることを想像してみてください。X線残留応力測定では、非破壊検査法を使用することでこのような知見を得ることができます。この記事では、X線回折技術によって内部応力を正確に測定し、製品の信頼性と寿命を向上させる方法について説明します。sin²ψ法やcosα法など、さまざまな手法によって正確な応力データが得られ、金属加工品が最高水準を満たすことを保証します。これらの高度な測定技術について、その原理、アプリケーション、および工業技術における利点を理解してください。
残留応力とは、工学でいう内部応力の一種です。ワークの残留応力分布は不均一であることが多く、静的強度、疲労強度、形状安定性、耐食性などに大きな影響を与えます。そのため、残留応力の測定は非常に重要です。
測定には主に2つの方法がある。 残留応力破壊試験と非破壊試験である。破壊試験法では、ワークピースの一部を除去し、その破壊強度を計算します。 残留応力 対応するひずみと変位に基づく。一般的な破壊試験法には ボーリング 方式とリングコア方式がある。
非破壊検査法では、残留応力と材料に変化をもたらす物理量(結晶面間隔、超音波伝播速度、透磁率など)との関係を確立し、残留応力を計算します。非破壊検査法には、X線回折法、中性子回折法、磁気法、超音波法などがあります。
X線回折法は、その成熟した原理と確立された手法、および実験室用機器、現場測定用の携帯型機器、特殊な状況用の特殊機器など、ますます高度化する検査機器の利用可能性により、残留応力測定に最も広く使用されている手法です。
残留応力を測定するためのX線回折法は、1929年にロシアの学者Akchenovによって初めて提案され、巨視的ひずみと格子ひずみを同一視しました。1961年には、ドイツの学者Macherauchがこの方法をさらに発展させました。2アクチェノフのアイデアに基づくψ法により、X線回折による残留応力測定は信頼性が高く、広く利用されている技術となっている。
過去60年の間に、X線回折はいくつかの異なる測定方法へと発展し、その結果、X線回折法は、様々な種類の測定方法へと進化してきた。2ψ法とcosα法が現在使われている2つの主な方法である。
残留応力を測定するためのX線回折技術を使いこなすには、そのさまざまな方法を理解することが重要です。
(1)X線回折残留応力測定法は、次の2つのアプローチに大別される。2ψ法とcosα法である。
(2) 罪2ψ法はさらに残留応力の計算方法によって、2θ法、d値法、ひずみ法に分類される。
(3) ψと2θの幾何学的関係から、sin2ψ法は、コチルト法とロール法の2種類に分けられる。
(4)測定方法は、X線管とカウンター管の走査モードに基づいて、固定ψ0法と固定ψ法に区別することもできる。
(5) ロール法には、標準ロール法、修正ロール法、ロール固定法ψの3つのサブカテゴリーがある。
(6)正負のψ測定法を用いてせん断応力τφを求める。
(7)X線回折は通常、特定の点における特定の方向の応力を測定するために使用されるが、ある点における主応力を測定する方法もある。
(8) スイング法は、ψ0スイング法、ψスイング法、デバイリングスイング法、φ角スイング法、X/Y往復並進法などのサブカテゴリーに分けられる。
(9)回折形状については、集光法、準集光法、平行ビーム法の3つのアプローチがある。
応力はひずみによって決まります。多結晶材料の場合、残留応力は該当領域の格子ひずみの統計的結果から推定されます。
したがって、残留応力は、X線回折法によって格子ひずみを測定することによって求めることができる。
材料の残留応力はマクロひずみを反映する。
マクロひずみは格子ひずみと等価である。
格子ひずみは結晶面間隔の相対的変化を表し、ブラッグ則に基づく回折装置を用いて計算できる。
残留応力を測定するためのX線回折法についてまとめました。
多結晶体に特定の波長(λ)のX線を照射すると、図1に示すように、特定の回折角(2θ)で反射X線の最大強度(回折ピーク)が観測される。この現象をX線回折という。
X線波長(λ)、結晶面間隔(d)、ブラッグ角(θ)の関係は、以下の式(1)で表される。

残留応力のX線回折分析では、X線管に適切なターゲット材料を選択し、適切な波長(λ)を決定します。次に、回折装置を用いて回折角(2θ)を測定します。この測定結果に基づいて、該当する結晶面の結晶面間隔(d)を算出することができます。

図1 X線回折ジオメトリー
光学の反射法則に従い、回折に関与する結晶面の法線は、図2に示されるように、入射光線と反射光線の二等分線上になければならない。
回折結晶面の法線と試料表面の法線のなす角は、回折結晶面の法線の方位角として知られており、通常ψで表される。

図2 X線回折結晶面方位ψの模式図
ブラッグの法則は、特定の方位(ψ)にある結晶面の間隔(dψ)を決定することができる。
無応力状態での結晶面の間隔(d0)がわかっていれば、指定方位での格子ひずみ(εψ)を計算することができます。
S1、S2、S3は試料表面の軸であり、S1は研究者によって定義される。
図3は、X線回折による残留応力測定に使用した座標系を示しています。

図3 X線回折応力測定の座標系
一般化されたフックの法則によれば、これらの結晶面のひずみは、点Oにおける応力テンソルの影響を受け、φとψの正弦と余弦、材料のヤング率、ポアソン比と密接に関係している。
したがって、応力(σφ)を含む点Oの3次元応力を決定することができる。
OP方向のひずみの式は、弾性理論から導くことができる。
ほとんどの材料や部品では、X線の透過深度は数ミクロンから数十ミクロンであるため、一般にσ33=0.
したがって、OP方向のひずみは式(2)で表される。


罪2ブラッグの法則と弾性理論に基づき、ψ法の公式を導き出した。
弾性理論で考慮される対象は、均質で連続的な等方性媒体と仮定される。
しかし、この仮定は多結晶体に対してのみ有効である。 金属材料 粒度が細かく、テクスチャーがない場合。
図4は、εの関数曲線である。n そして罪2ψは、等方性材料、応力勾配または組成勾配を持つ材料、せん断応力を持つ材料、およびテクスチャを持つ異方性材料に適用されます。

図4c)に示すように、せん断応力τ13≠ 0, τ23≠0とsin2ψ曲線は±ψ分岐、σφ とτφ は、測定されたひずみデータ ε﹢ψ とε-ψ 式(4)および式(5)で示されるように、一連の±ψ角で。

重要なのは、その罪が2図4cに示すψ曲線)は、±ψ分岐を持つ可能性は低い。
これは、回折に使用されるX線が被検査材への透過深さに限界があるためで、通常は数ミクロンから数十ミクロン程度に過ぎない。
その結果、材料表面に垂直な応力成分はゼロとみなすことができる。
特殊な加工(強力で大きな切削量の研削など)の条件下で、主応力面が試験片の表面からずれた場合にのみ、τ13≠0とτ23≠0が発生する。
また、±ψ分岐は一般的ではなく、フィッティングカーブには楕円の属性がないことが多い。これはゴニオメータの±ψ機構の系統誤差によるところが大きい。したがって、楕円フィッティングの重要性を過度に強調する必要はない。
結論として、X線回折によって残留応力を決定する実用的かつ実行可能なプロセスは、いくつかのψ角(またはいくつかの±ψ角の組)を選択し、対応する回折角(2θφψ)を測定し、その後計算することである。
学者たちは、ψ平面と2θ平面の間の空間幾何学的関係を整え、回折曲線を決定し、計算を行うための様々な方法を開発してきた。
回折角2θφψ をX線回折装置で測定し、対応する結晶面間隔をdφψ ブラッグの法則に従えば、格子ひずみ εφψ は、式(6)に示すように、結晶面間隔によって表すことができる。

真のひずみを式(3)、式(4)、式(5)に直接代入して応力を計算するのが真のひずみ法の式です。
真のひずみ法を採用し、d0 とθ0 は必要ない。
ほとんどの場合、真のひずみ法は大きな利点がある。
式(7)および式(8)に示すように、近似式を使用してひずみを計算することもできる。

2θ法の計算式を式(9)に示す。

ここで、Kは応力定数であり、その計算式は式(10)で示される。

ここで、νは材料のポアソン比である。
材料によっては、θ0 は化学組成によって大きく変化するため、応力定数を使用した場合、結果は大きく乖離する。
真ひずみ法は、欧州連合規格EN 15305-2008 Non destructive testing - Test method for residual stress analysis by X-ray diffractionおよびGB/T 7704-2017 Non destructive Testing X-ray Stress Measurement Methodに含まれています。
国産応力計XL-640は、デフォルトの応力計算方法として真ひずみ法を、計算方法として2θ法を選択することができます。
コプラナー法は、図5に示すように、2θ平面がψ平面(応力方向平面)と一致する測定方法である。

図5 同傾斜法の幾何学図
同じ傾斜法で、X線入射角ψ0 が支配的であり、角度ψは式(11)と式(12)に示すように計算できる。

実際のワークの応力試験では、試験点が同じような浅い溝にある場合、ゴニオメータの試験スペースは限られているため、同じ傾斜方法が適している。
ロール法は、図6に示すように、2θ平面とψ平面(応力方向平面)が直交する測定方法である。

図6 ロール法の幾何学図
ロール法(χ法)の大きな特徴は、回折ピークの吸収係数が小さいことで、測定精度の向上に寄与している。
2θおよびψレンジは、必要に応じて完全に拡張することができます。材料によっては、ピーク位置の低い回折光線(145°以下のピークなど)を応力測定に利用できます。
しかし、この方法の2θ平面とψ平面は互いに垂直であり、3次元空間を必要とするため、狭い空間の測定に適用するのは困難である。
ある外資系企業のストレス測定器製品は、図7に示すように、ダブル検出器を用いた改良型ロール方式を採用している。その幾何学的レイアウトは図に描かれている。

図7 モディファイド・ロール法の幾何学図
1977年1月には早くも、中国科学院金属研究所の李家宝が、式(13)と式(14)に示すようなこの試験方法と計算式を提案している。
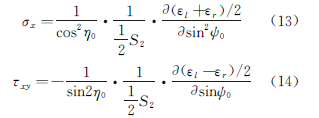
ロール法は、固定ψ0法と固定ψ法に分けられる。
固定ψ法は、より正確な原理と実際の効果的な結果から、固定ψ0法よりも優れていると考えられている。
この2つの方法、ロール固定ψ法を組み合わせることで、吸収係数を1にすることができる。
つまり、テクスチャーがない限り、角度ψが変わっても、回折ピークが奥底に傾くことはなく、ピーク形状は対称のままであり、ピーク形状と強度は変化しない。
この特徴は測定精度を大幅に向上させ、ロール固定ψ法を理想的な測定技術にしている。
スイング法とは、各設定角度ψ(またはψ0角)を中心点として、X線管と検出器を左右に一定角度(±Δψまたは±Δψ0)ずつスイングさせる方法である。
この方法は、回折に参加する結晶粒の数を増やし、粗粒材料の応力測定に有効な方法となる。
φ角スイング法やX/Y平行移動スイング法など、他のスイング法も使用可能で、異なるスイング法を組み合わせてテストすることもできる。
2012年、日本に本社を置くパルステック社は、初めて二次元検出器技術を利用したストレス測定器を発表した。
この装置は、X線回折情報を収集するために単一入射モードと2次元検出器を使用して動作し、テストポイントでのデバイリングデータを迅速に収集することができます。
結晶面法線と試料表面法線がなす角度ψは、デバイ環上の各点で同一平面上にないため、sin2ψ法は応力計算に使用できません。代わりに、角度α(cosα)法が採用されます(図8に示すように)。
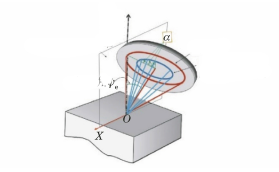
図8 方法cosαの幾何学図
この試験方法は、大型鋼構造物の表面応力を測定するのに理想的である。
しかし、粗粒の材料やテクスチャーのある材料を試験する場合には限界がある。
cosα法は、式(15)と式(16)で示されるように、弾性の原理に基づいている。

図9は、「完全2位置検出器」(入射角45°)を使用して取得できる角度ψの最大範囲を示している。
角度αはデバイリング平面上にあり、デバイリング上の各点の中心角である。

図9 メソッドsinのデータポイントの位置2ψ in s curve
X線回折による残留応力測定法は、どちらも同じ力学的原理に基づいている。
ひずみテンソルは空間角で変換することができ、cosα法で使用されるα角は完全にψ角に変換することができる。
要するに、cosα法は本質的にsinα法の近似である。2ψメソッド。
一般的に、熱延鋼板にはテクスチャーがないと考えられている。しかし 鋼板 は、さまざまな要因によって質感を示すことがある。
にもかかわらず、多くのユーザーは、このような場合にX線回折を使用して残留応力を測定することを選択します。
例えば、テクスチャを有する熱延鋼板を選択した場合、試験条件と結果は表1および表2に示す通りである。各装置によるZ点(0)での残留応力測定の試験報告書を図10〜13に示す。
表1 熱間残留応力測定のための試験パラメータ 圧延スチール さまざまな応力測定器によるプレート
| 設備タイプ | μ-X360S | プロトLXRD | X-レイボット | XL-640 |
| 試験方法 | cosα | 罪2ψ | 罪2ψ | 罪2ψ |
| 電圧/kV | 20 | 30 | 20 | 25 |
| 電流/mA | 1 | 25 | 1 | 6 |
| 照射スポット/mm | 1 | 1 | 1 | 1 |
| ψ レンジ/(°) | – | -35~35 | -40~40 | 0~45 |
| ひずみ計算方法 | – | Dバリュー法 | ストレイン法 | ストレイン法 |
| ピーク判定法 | – | パーソンVII | 中間点 | 相互相関法 |
| 残留応力/MPa | 78 | 213.6 | 144 | 113 |
表2 異なる応力測定器で測定した熱延鋼板の残留応力
| テストポイント | μ-X360S | プロトLXRD | X-レイボット | XL-640 |
| Z(5) | 29,47 | 122 | 107 | 77 |
| Z(4) | 37,52 | 135 | 112 | 70 |
| Z(3) | 74,70 | 104 | 95 | 67 |
| Z(2) | 38,28 | 153 | 99 | 134 |
| Z(1) | 37,64 | 166 | 122 | 101 |
| Z(0) | 64,78 | 144 | 213 | 113 |
| Z(-1) | 72,71 | 138 | 97 | 139 |
| Z(-2) | 62,52 | 134 | 83 | 145 |
| Z(-3) | 75,70 | 120 | 93 | 153 |
| Z(-4) | 63,56 | 114 | 80 | 148 |
| Z(-5) | 79,27 | 94 | 93 | 152 |

図10 μ-X360S型応力計で測定したZ(0)点のデバイリング

図11 2θ-sin2プロトLXRD応力計で測定したZ (0)のψ曲線

図12 2θ-sin2X-RAYBOT応力計による測定点Z (0)のψ曲線

図13 ε-シン2応力計XL-640で測定したZ (0)のψカーブ
c法で測定した残留応力は、s法で測定した残留応力よりも小さい。
Z (0)のテストポイントには、応力計が使用される。の等間隔性の原則に従う。2ψ、8ψ角は0°~45°の範囲で選択。
結果を図14-15に示す。図14-15に示すように2素材のψカーブは、テクスチャーによる「ショック」タイプを示す。
罪の縦座標2図13のψ曲線はひずみεであり、縦軸を2θに変更後、リニアフィッティングを行う。結果を図14に示す。
フィッティング直線の傾きMは-0.355、残留応力σは113MPaである。

図14 2θ-sinのフィッティング結果2応力計XL-640によるZ点(0)でのψ曲線の測定値
μ-X360S応力計で選択されたψ範囲は、遮蔽の最初の2つの2θ値に相当し、その後、直線フィッティングが行われる。結果を図15に示す。

図15 2θ-sinのフィッティング結果2μ-X360S型応力測定器によるZ (0)のψ曲線
PROTO LXRD応力計を使用して、選択したψ範囲をテストし、図14の最後の3つの2θ値を遮蔽し、線形フィッティングを実行します。結果をFig.16に示す。

図16 2θ-sinのフィッティング結果2Z (0)点でPROTO LXRD応力計により測定されたψ曲線
図12からわかるように、最大sin2X-RAYBOT応力計で測定したZ点(0)のψ値は0.4。
選択したψの範囲に従って、図14の最後の2つの2θ値を遮蔽し、線形フィッティングを行う。結果を図17に示す。

図17 2θ-sinのフィッティング結果2X-RAYBOT応力計で測定したZ (0)のψ曲線
素材の質感のため、その罪は重い。2ψカーブは振動的である。
選択したψ角の範囲が異なるため、フィッティングラインから得られる勾配と残留応力値に違いが生じる。
未知のテクスチャーや粗い結晶粒を持つ材料の場合、残留応力測定に狭いψ範囲と少数のψステーションを選択することは、大きな測定誤差につながる可能性があるためお勧めできません。
リニアフィッティングは、テクスチャーのある素材には適さない場合があります。2ψカーブは振動的である。
測定プロセスでは、振動や測定誤差による変動を軽減するために、しばしばリニアフィッティングが使用される。
ψの角度を45°にすることは、浸透深度に影響される可能性があるため、実行不可能かもしれない。貫入深さを無視できるのであれば、角度を大きくした方がより正確な結果が得られる可能性が高い。
粗い結晶粒やテクスチャーを持つ材料の場合、非線形ε-sinの影響を排除するために、ψ角の範囲をできるだけ拡大する必要がある。2ψ分布。これは±ψ角の両方を測定することで達成できる。
フィッティングされた直線の精度は、回帰のフィッティングに最小二乗法を使用し、ψの範囲とψステーションの数の両方を増やすことによって向上させることができる。これにより、より信頼性の高いテスト値が得られる。
測定精度は、X線照射面積を増やすか、スイング法で参加する回折粒の数を増やすことによっても向上させることができる。
(1) 罪2ψ法は、ψの範囲を広げ、より多くのψステーションを選択することで、精度を向上させた残留応力の測定に使用できます。しかし、この方法は1回の暴露を伴うため、ψの範囲が十分でない場合、測定誤差が大きくなる可能性があり、限界があります。
(2) sinを利用する測定法では2原理的には、ロール法はチルト法よりも優れている。測定点のスペース条件が許す限り、ロール法を使用することをお勧めします。特定の部品の溝の残留応力を測定する場合は、共傾斜法が一般的に使用されます。
(3) 残留応力の計算には、真ひずみ法が好ましい。
(4) この目的のためには、sin2ψ法が標準的な方法とされている。最も正確な結果を得るためには、角度ψをsin2ψ値二等分法で、できるだけ多くのψ角を測定すること。