Are you struggling to design accurate sheet metal parts? Unlock the secrets of the K-factor, a crucial concept in sheet metal fabrication. In this article, our expert mechanical engineer demystifies the K-factor, explaining its relationship to the neutral layer and providing practical methods for calculation. Discover how mastering the K-factor can revolutionize your sheet metal designs and ensure successful manufacturing.
This article provides an in-depth exploration of the K-factor, a crucial concept in sheet metal design and fabrication. It covers the definition of the K-factor, its relationship to the neutral layer, and methods for calculating and calibrating the K-factor.
The article also discusses the factors influencing the K-factor, such as material properties and bending parameters, and provides practical guidance for determining the optimal K-factor value for various applications.
The K-factor is a crucial concept in sheet metal design and fabrication, particularly when working with CAD software like SolidWorks. It represents the location of the neutral axis within a bend and plays a vital role in determining the accurate length of sheet metal parts after bending. Mathematically, the K-factor is defined as the ratio of the distance between the neutral layer and the inner surface of the bend (t) to the overall thickness of the sheet metal (T):
K = t / T
This dimensionless value always falls between 0 and 1, typically ranging from 0.3 to 0.5 for most common materials and bending processes. The K-factor is essential for several reasons:
Factors influencing the K-factor include material properties (such as yield strength and ductility), sheet thickness, bend radius, and bending method (air bending, bottoming, coining). Modern sheet metal fabrication often utilizes empirically derived K-factor tables or advanced finite element analysis (FEA) to determine optimal values for specific applications.
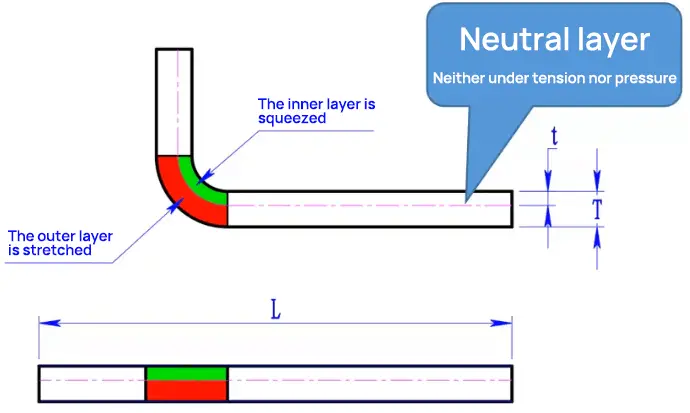
To fully grasp the K-factor, it’s essential to understand the concept of the neutral layer. When a sheet metal part is bent, the material near the inner surface of the bend undergoes compression, with the severity increasing closer to the surface. Conversely, the material near the outer surface experiences stretching, with the intensity increasing nearer to the surface.
Assuming the sheet metal is composed of thin stacked layers (as is the case with most metals), there must exist a layer in the middle that experiences neither compression nor stretching during bending. This layer is known as the neutral layer. The neutral layer is critical in determining the K-factor and, consequently, the bend allowance and flat pattern dimensions of a sheet metal part.
The neutral layer, though invisible within the sheet metal, plays a pivotal role in bending operations and is intrinsically linked to the material’s properties. This relationship directly influences the K-factor, a critical parameter in sheet metal fabrication.
The position of the neutral layer is determined by several material characteristics:
The K-factor, being a representation of the neutral layer’s position, is consequently influenced by these same material properties. It’s typically expressed as a decimal between 0 and 1, where 0.5 indicates the neutral layer at the sheet’s mid-thickness.
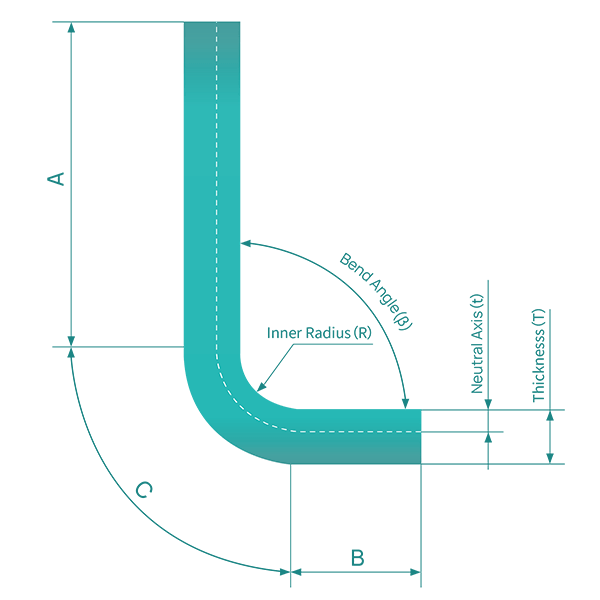
A fundamental principle derived from the neutral layer concept is that the unfolded (flat pattern) length of a bent sheet metal part equals the length of the neutral layer. This can be mathematically expressed as:
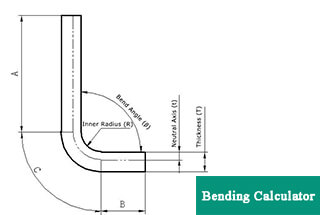
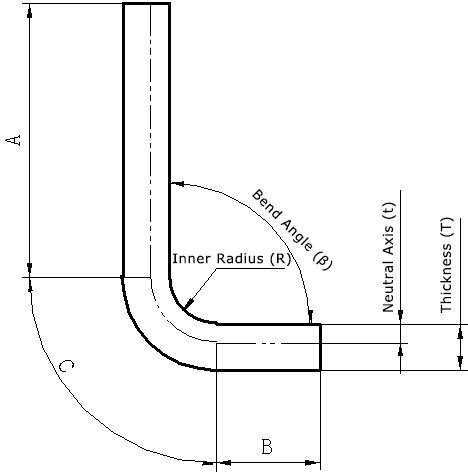
Unfolded length = straight length A + straight length B + arc length C
Where:
This relationship is crucial for precise flat pattern dimensioning, which relies on accurate K-factor determination and bend allowance calculations. The bend allowance, in turn, is influenced by:
Understanding these interrelationships enables engineers to:
In practice, while theoretical calculations provide a starting point, empirical testing and adjustment of K-factors for specific material-tooling combinations often yield the most accurate results in production environments.
The illustrations below provide a detailed visual explanation of the K-factor concept:
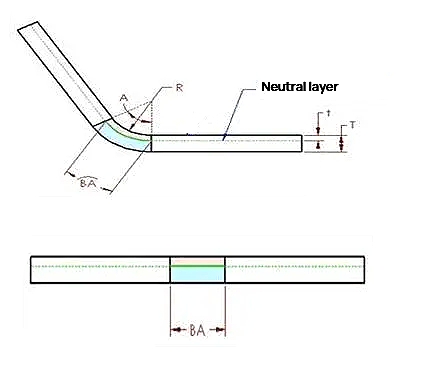
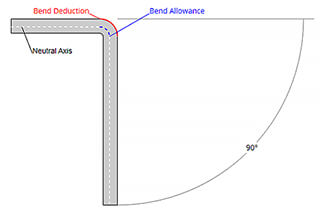
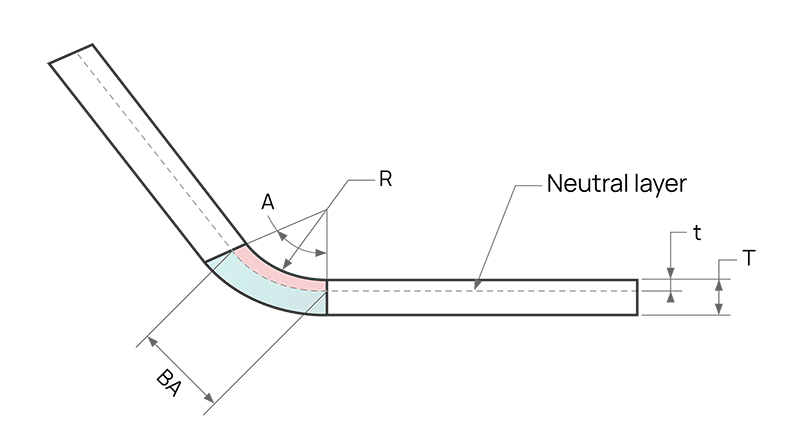
In the cross-section of a sheet metal part, there exists a neutral layer or axis. The material at this neutral layer within the bend region experiences neither compression nor stretching, making it the only area that remains undeformed during bending. In the diagram, the neutral layer is represented by the intersection of the pink (compression) and blue (stretching) regions.
A key insight is that if the neutral layer remains undeformed, the arc length of the neutral layer within the bend region must be equal in both the bent and flattened states of the sheet metal part. This principle forms the basis for calculating bend allowances and flat pattern dimensions using the K-factor.
Therefore, the bending allowance (BA) should be equal to the length of the neutral layer arc in the bending area of the sheet metal part. This arc is represented as green in the Figure.
The position of the neutral layer in sheet metal depends on specific material properties, such as ductility.
Assuming the distance between the neutral sheet metal layer and the surface is “t,” that is, the depth from the surface of the sheet metal part to the sheet metal material in the thickness direction is t.
Therefore, the radius of the neutral sheet metal layer arc can be expressed as (R+t).
Using this expression and the bending angle, the length of the neutral layer arc (BA) can be expressed as:
To simplify the definition of the neutral layer in sheet metal and considering the applicability to all material thicknesses, the concept of the k-factor is introduced. Specifically, the k-factor is the ratio of the thickness of the neutral layer position to the overall thickness of the sheet metal part, that is:
Therefore, the value of K is always between 0 and 1. If a k-factor is 0.25, it means that the neutral layer is located 25% of the thickness of the sheet metal material, and if it is 0.5, it means that the neutral layer is located at the halfway point of the entire thickness, and so on.
Combining the above two equations, we can get the following equation:
Where some values such as A, R, and T are determined by the actual geometric shape.
To accurately determine the K-factor value, we offer two precision calculators designed for different input scenarios. While the results may exhibit slight variations, both calculators provide reliable outcomes tailored to your specific metal forming requirements.
Calculator 1: Known Bend Allowance and Inside Bend Radius
This calculator is optimized for situations where you have precise measurements of the bend allowance and inside bend radius. It utilizes these parameters to compute the K-factor and the critical distance from the inside surface to the neutral axis (t), essential for accurate sheet metal bending calculations.
Inputs:
Outputs:
If you only know the inside bend radius and material thickness, use this calculator to determine the K-factor.
Inputs:
Outputs:
These calculators provide a convenient way to quickly determine the K-factor and neutral axis position for your sheet metal design projects.
Based on the previous calculations, we can derive the formula for calculating the K-factor:
Where:
Sample calculation:
Let’s work through a sample calculation using the following given information:
The formula to calculate the K factor is:
Step 1: Substitute the given values into the K-factor formula:
K = (2.1 × 180/(3.14 × 90) – 1)/1
Step 2: Simplify the equation:
K ≈ 0.337
Therefore, for the given parameters, the K-factor is approximately 0.337.
This example demonstrates how to apply the K-factor calculation formula to determine the K-factor for a specific sheet metal bending scenario.
The following are K-factors for common metal materials.
K factor chart
| Thickness (SPCC/SECC) | K Factor (All angles, including R angle) |
| 0.8 | 0.615 |
| 1 | 0.45 |
| 1.2 | 0.35 |
| 1.5 | 0.348 |
| 2 | 0.455 |
| 3 | 0.349 |
| 4 | 0.296 |
| Thickness (SPCC/SECC) | Bend deduction (only applicable to 90 corners) |
| 0.8 | 1 |
| 1 | 1.5 |
| 1.2 | 2 |
| 1.5 | 2.5 |
| 2 | 3 |
| 3 | 5 |
| 4 | 7 |
| 5 | 10 |
The following table provides bend allowance values obtained by a specific manufacturer for various materials and thicknesses. Please note that these values are for reference only and may not be universally applicable.
| Material thickness (T) | SPCC | Al | SUS | Copper |
| 0.8 | 1.4 | 1.4 | 1.5 | – |
| 1.0 | 1.7 | 1.65 | 1.8 | – |
| 1.2 | 1.9 | 1.8 | 2.0 | – |
| 1.5 | 2.5 | 2.4 | 2.6 | – |
| 2.0 | 3.5 | 3.2 | 3.6 | 37 (R3) |
| 2.5 | 4.3 | 3.9 | 4.4 | – |
| 3.0 | 5.1 | 4.7 | 5.4 | 5.0 (R3) |
| 3.5 | 6.0 | 5.4 | 6.0 | |
| 4.0 | 7.0 | 6.2 | 7.2 | 6.9 (R3) |
Note: For copper, the bend allowance values are coefficients when the inner bend radius is R3. When using an acute punch for bending, refer to the bend allowance for aluminum alloy or determine the value through trial bending.
To understand why the K-factor cannot exceed 0.5, it’s crucial to comprehend the concepts of the K-factor and the neutral layer in sheet metal bending.
Sheet metal bending involves creating a controlled deformation to form a small radius arc. Unlike roll forming, which produces larger radii, bending typically results in tighter curves. Regardless of the bending method employed (air bending, bottoming, or coining), achieving a perfect right angle is physically impossible due to material properties and tooling limitations. The workpiece radius is directly correlated to the lower die radius – a smaller die radius produces a tighter bend radius, and vice versa.
In sheet metal bending, the material undergoes both compression on the inside of the bend and tension on the outside. This deformation creates a theoretical plane within the material thickness where neither compression nor tension occurs – this is known as the neutral layer or neutral axis.
When a sheet is bent, the inner surface dimensions decrease while the outer surface dimensions increase. This dimensional change gives rise to the bend allowance, a critical factor in precise bend calculations. For instance, when bending a 90-degree angle from a flat blank with outside dimensions of 20 x 20 mm, the unfolded length will always be less than 40 mm, regardless of material thickness. This is due to the elongation of the outer fibers during bending.
Advanced research and high-precision manufacturing requirements have revealed that the neutral layer’s position is not always at the exact center of the material thickness. In fact, for small bend radii (typically when the inside bend radius is less than 2 times the material thickness), the neutral axis shifts towards the inside of the bend.
This shift occurs because the compressive forces on the inside of the bend are greater than the tensile forces on the outside, resulting in an asymmetrical strain distribution. For example, in a tight bend, the inside dimension might decrease by 0.3 mm, while the outside dimension increases by 1.7 mm, rather than equal 1 mm changes on both sides.
The K-factor is a dimensionless coefficient used to locate the position of the neutral layer within the material thickness during bending. It is defined as the ratio of the distance from the inside surface of the bend to the neutral layer, divided by the total material thickness.
Mathematically, K-factor = d / t, where:
d = distance from inside bend surface to neutral layer
t = total material thickness
The neutral layer’s position is constrained by the physical boundaries of the material. At its theoretical maximum, the neutral layer could be located at the exact center of the material thickness. In this case:
d (maximum) = t / 2
K-factor (maximum) = (t / 2) / t = 0.5
Therefore, the K-factor in sheet metal bending cannot exceed 0.5, as this would imply the neutral layer is positioned beyond the centerline of the material thickness, which is physically impossible.
In practice, K-factors typically range from 0.3 to 0.5, depending on material properties, bend radius, and forming process. Accurate determination of the K-factor is crucial for precise bend allowance calculations and achieving tight dimensional tolerances in sheet metal fabrication.
Even for the same material, the K-factor in actual processing is not constant and is affected by the processing technology. In the elastic deformation stage of sheet metal bending, the neutral axis is located at the middle of the plate thickness. However, as the bending deformation of the workpiece increases, the material undergoes mainly plastic deformation, which is unrecoverable.
At this point, the neutral layer shifts towards the inner side of the bend as the deformation state changes. The more severe the plastic deformation, the greater the inward offset of the neutral layer.
To reflect the intensity of plastic deformation during plate bending, we can use the parameter R/T, where R represents the inner bend radius and T represents the plate thickness. A smaller R/T ratio indicates a higher level of plate deformation and a greater inward shift of the neutral layer.
The table below shows data for plates with a rectangular cross-section under specific processing conditions. As R/T increases, the neutral layer position factor K also increases.
| R/T | K |
| 0.1 | 0.21 |
| 0.2 | 0.22 |
| 0.3 | 0.23 |
| 0.4 | 0.24 |
| 0.5 | 0.25 |
| 0.6 | 0.26 |
| 0.7 | 0.27 |
| 0.8 | 0.3 |
| 1 | 0.31 |
| 1.2 | 0.33 |
| 1.5 | 0.36 |
| 2 | 0.37 |
| 2.5 | 0.4 |
| 3 | 0.42 |
| 5 | 0.46 |
| 75 | 0.5 |
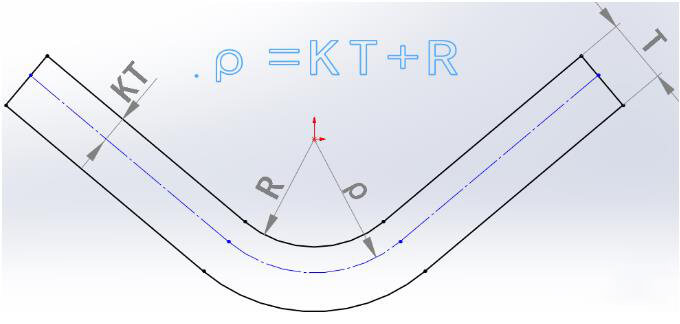
The radius of the neutral layer (ρ) can be calculated using the following formula:
ρ = R + KT
Where:
Once the neutral layer radius is determined, its developed length can be calculated based on geometry, and subsequently, the sheet’s developed length can be derived.
Generally, under the same bending conditions, softer sheet metal materials have lower K values and larger inward offsets of the neutral layer.The Machinery’s Handbook provides three standard bending tables applicable to 90-degree bending, as shown below:
| Table | Material | K Factor |
| # 1 | Soft brass, copper | 0.35 |
| # 2 | Hard brass, copper, mild steel, aluminum | 0.41 |
| # 3 | Hard brass, bronze, cold rolled steel, spring steel | 0.45 |
These tables demonstrate how material properties influence the K-factor and the neutral layer position.
For bends with smaller inner radii, the bend angle can also affect the change in the K-factor. As the bend angle increases, the neutral layer experiences a greater offset towards the inner side of the bend. This relationship between bend angle and neutral layer shift is particularly significant for tight-radius bends and should be considered when determining the appropriate K-factor for a given sheet metal part.
In sheet metal bending operations, calibrating the K-factor is crucial for achieving precise and consistent results. This calibration process is essential due to several factors inherent in metal forming:
By investing time in K-factor calibration, manufacturers can significantly improve the accuracy of their sheet metal bending calculations, enhance product quality, and optimize their design-to-manufacturing workflow. This calibration process, while initially requiring some effort, ultimately saves time and resources by reducing errors and iterations in the sheet metal fabrication process.
Here’s a comprehensive analysis of the K-factor calibration process for sheet metal design in SolidWorks:
By meticulously following this calibration process, you ensure accurate sheet metal modeling in SolidWorks, leading to precise flat pattern development and optimized manufacturing processes.
To determine the optimal K-factor value for sheet metal bending based on different material properties, it’s essential to understand the role and significance of the K-factor. The K-factor is a standalone value that describes how sheet metal bends and unfolds under various geometric parameters. It’s also used to calculate bend compensation for different material thicknesses, bend radii, and bend angles. Choosing the appropriate K-factor is crucial for ensuring accurate unfolding and bending of sheet metal parts.
The process of determining the optimal K-factor value based on material properties can be summarized in the following steps:
By following these steps and considering the material properties, default values, experimental adjustments, bend deduction tables, and additional bending parameters, you can determine the optimal K-factor value for your specific sheet metal bending application.
Q: What is the typical range of K-factor values for common materials?
A: The K-factor typically ranges from 0.3 to 0.5, depending on the material properties and forming conditions. For soft, ductile materials like annealed copper and aluminum, K-factors are generally lower, around 0.33 to 0.38. Medium-strength materials such as mild steel and brass typically have K-factors between 0.40 and 0.45. High-strength materials like stainless steel and spring steel tend to have higher K-factors, ranging from 0.45 to 0.50. It’s important to note that these values can vary based on factors such as sheet thickness, bend radius, and grain orientation.
Q: How do I choose the appropriate K-factor for my sheet metal design?
A: Selecting the appropriate K-factor involves considering multiple factors:
Always validate your selected K-factor through prototyping or sample production before full-scale manufacturing to ensure accuracy and quality in the final parts.
In conclusion, the K-factor is a critical concept in sheet metal design and fabrication, serving as a key parameter for accurately predicting material behavior during bending operations. By understanding its relationship to the neutral axis position, material properties, and forming conditions, designers and engineers can create precise flat patterns and achieve optimal bend allowances.
Mastering the nuances of K-factor selection and application is essential for producing high-quality sheet metal parts with consistent dimensional accuracy and performance. As manufacturing technologies and materials continue to evolve, staying informed about the latest research and industry best practices regarding K-factor determination will remain crucial for maintaining competitive edge in sheet metal fabrication.
Further Reading and Resources
To deepen your understanding of sheet metal bending and related concepts, explore the following resources:
As the founder of MachineMFG, I have dedicated over a decade of my career to the metalworking industry. My extensive experience has allowed me to become an expert in the fields of sheet metal fabrication, machining, mechanical engineering, and machine tools for metals. I am constantly thinking, reading, and writing about these subjects, constantly striving to stay at the forefront of my field. Let my knowledge and expertise be an asset to your business.
EN 
DE 
ES 
FR 
IT 
NL 
PT 
RU 